基于正交约束的导航接收机空时自适应方法
张柏华马红光孙新利谭巧英潘寒尽
①(第二炮兵工程大学 西安 710025)
②(空军95100部队 广州 510405)
③(中国兵器装备集团摩托车检测技术研究所 西安 710032)
④(总参陆航研究所 北京 101121)
基于正交约束的导航接收机空时自适应方法
张柏华*①②马红光①孙新利①谭巧英③潘寒尽④
①(第二炮兵工程大学 西安 710025)
②(空军95100部队 广州 510405)
③(中国兵器装备集团摩托车检测技术研究所 西安 710032)
④(总参陆航研究所 北京 101121)
卫星导航系统容易受到干扰,空时自适应处理在导航接收机抗干扰方面拥有明显的优势,即系统自由度显著提高,但是传统空时自适应处理应用于导航接收机抗干扰中却面临信号失真的难题。该文提出一种基于正交约束的导航接收机空时自适应处理方法。该方法从空时自适应处理的原理入手修改传统空时自适应处理优化的约束项,消除了不同时延信号对合成信号的影响,保证了空时自适应处理在有效抑制干扰的同时不影响导航信号的捕获和解码。理论分析和仿真结果表明,该方法能有效解决空时自适应处理中的导航信号失真问题。
卫星导航系统;正交约束;导航接收机;信号失真;空时自适应处理;抗干扰
1 引言
卫星导航能为陆地海洋和空间的用户提供全天候、全时间、连续的高精度3维位置、3维速度和时间信息,具有其它导航方式不可比拟的优势,近年来在社会生活的各个领域均得到了广泛的应用,尤其是军事方面[1]。1994年3月,美国第2代卫星导航系统——全球卫星定位系统(GPS)建成。俄罗斯(前苏联)也在1996年建立了自己的全球卫星导航系统(GLONASS)。欧盟出于政治、军事、经济方面的考虑,建设了伽利略卫星导航系统(GALILEO)。据公开报道,我国的北斗二代卫星导航系统已经发射了10多颗卫星,将于2015年具备区域导航能力,2020年具备全球导航能力。北斗二代卫星导航系统对我军的信息化建设意义重大,特别是对提高各种远程打击武器的精确制导能力有现实意义。然而,由于卫星距离地球表面大约20000 km,卫星导航接收机接收到的卫星信号十分微弱,只有-160 dB左右,比接收机热噪声还要弱20~30 dB[2,3]。因此,卫星导航信号很容易受到干扰的影响,从而使卫星导航接收机无法发挥精确定位的功能。提高卫星导航系统的抗干扰能力已经成为新一代卫星导航系统的核心。
近年来,国内外对卫星导航系统抗干扰技术的研究很多[2−19],提高卫星导航系统抗干扰能力的方法主要有:增强卫星信号的发射功率、采用加密的军用码、采用伪卫星技术。提高卫星导航接收机的抗干扰能力的方法主要有:采用阵列天线技术,提高空域滤波能力;采用自适应干扰检测、自适应滤波(时域、频域)等手段减小干扰;直接捕获军用码;采用卫星导航/惯性导航组合方案[9]。基于阵列信号处理的自适应滤波方法是目前比较常用的抗干扰方法,特别是空时自适应处理(Space Time Adaptive Processing, STAP),在不增加阵元数量的同时可以极大提高系统的抗干扰自由度,因而成为GPS 抗干扰技术的一个发展趋势[7−19],这对于弹载等环境有着重要的意义。然而,由于STAP加入了延迟时间信号,应用传统的STAP将会导致严重的信号失真,导致定位误差不可接受,国内外学者对STAP导致的信号失真问题进行研究,文献[7]提出均衡补偿的方法(本文称为Fante方法),文献[10]提出群时延约束方法对所有卫星信号的失真进行均衡,文献[11]提出一种逆滤波器补偿算法,文献[12]提出基于同态滤波的STAP补偿方法,文献[13]分析讨论了空时自适应处理对P(Y)码GPS信号的影响,文献[14]提出从相关峰波形估计误差的方法,文献[15]提出使用维纳滤波器对失真的相关函数进行补偿的方法。上述文献都有一个理想假设,即干扰能被彻底对消干净,而实际上,由于干扰未能对消干净将导致严重的性能衰退。另外,文献[12]中的式(17)有问题,在某一时刻,空时处理后的数据是标量,而其文中的信号和不同时间延迟的响应系数均为矢量。可以说,STAP导致的导航信号失真这个问题仍然没有得到很好的解决。本文从STAP原理的源头入手修改优化的约束项,提出基于正交约束的导航接收机STAP (Orthogonal Constraint based technique for Space Time Adaptive Processing, OS-STAP)。
2 空时自适应处理对导航信号的影响
传统STAP的应用背景是机载脉冲多普勒雷达的地(海)杂波抑制,此时,空时自适应处理不影响不同时间到达的脉冲信号。对于导航信号,STAP则是将1维的空域滤波推广到空间和时间的2维域中,形成STAP结构,从而极大提高抗干扰的自由度,假设一个N个阵元的等距线阵,空时联合处理时采用K个延迟数据,其结构如图1所示[20]。此时,本文发现一个矛盾:利用不同时刻的信号可以增加抗干扰自由度,但是利用不同时刻信号合成某一时刻的信号却会导致导航信号的失真。
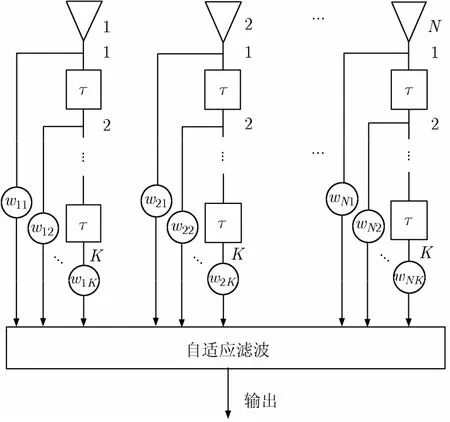
图1 空时自适应处理抗干扰原理图
STAP的信号模型可以表示为
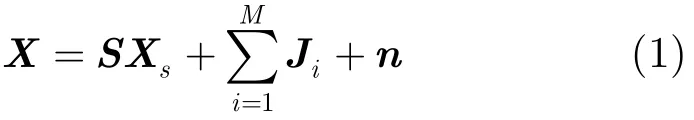
X=[x11,x21,…,xN1,x12,x22,…,xN2,…,x1K,x2K,…,xNK]T是阵列接收到的空时数据矢量;n是加性高斯白噪声;Xs=[Xs0,Xs1,…,Xs(K−1)]T表示K个延迟卫星信号矢量;Ji表示第i个干扰信号及其色散多径干扰构成的NK×1维矢量。
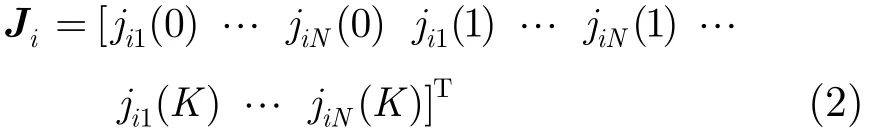
其中

是NK×K阶矩阵。
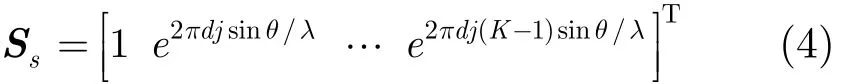
是导航信号的空域导向矢量,d表示阵元间距,λ表示载波波长。
STAP可以有效抑制干扰,但同时也会对导航信号造成影响,令空时权矢量为
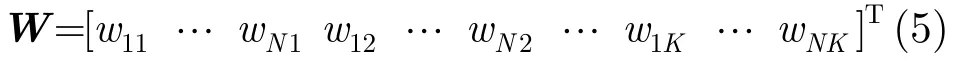
则经过STAP抗干扰后的阵列输出为
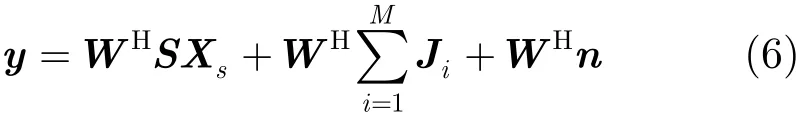
此时,即使干扰可以抑制得差不多,常规的STAP方法也没有恢复出应有的信号,权值和导向矢量的乘积不是1,而是一个矢量,假设该矢量为h,
则有
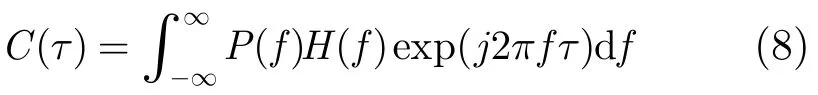
其中,P(f)是正的,关于f对称的,如果没有H(f)的影响,相关函数的峰值在τ=0。但是由于H(f)的存在,将导致相关峰位置的偏移、相关峰主瓣的展宽等,造成不能有效定位。
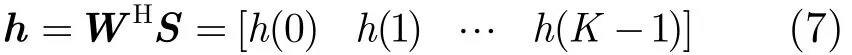
卫星导航的捕获和定位主要是通过伪随机信号的相关运算来实现,接收数据与已知信号的互相关函数为[7]
3 基于正交约束的导航接收机空时自适应
方法
针对导航信号STAP中的信号失真问题,国内外学者开展了相关研究,文献[7]提出串联有限冲击响应(FIR)滤波器来进行校正:G(f)=H*(f),这时,相关函数为
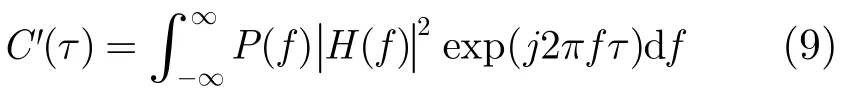
由于相关函数C'(τ)的峰值在τ=0不变,理想情况下只是造成相关函数主瓣的展宽。但是实际处理中由于干扰的作用串联滤波器并不能取得应有的效果,由于干扰残余的存在,该方法会失效。
文献[11]提出串联逆滤波器来进行校正,该方法与文献[7]所提方法是类似的,不同的是串联的滤波器G(f)变成了G(f)H(f)=δ,其求解是利用最小二乘法求出H(f)的广义逆。仿真发现,理想情况下该方法能取得良好的效果,但是当存在干扰时,特别是当干扰较强时,由于干扰残余的存在,该方法将失效。
文献[15]提出利用维纳滤波器对失真的相关函数进行补偿的方法,和文献[7]和文献[11]所提方法类似,其也面临干扰残余的问题,在非理想情况下,特别是干扰较强时,性能必然下降显著。并且,文献[15]仿真图10中未补偿的相关峰值未偏移,这是存疑的。
针对上述问题,本文从最初的空时自适应处理原理入手,对信号失真的问题进行初步探讨。
传统的最优处理器可以描述为如式(10)所示的数学优化问题[20]:

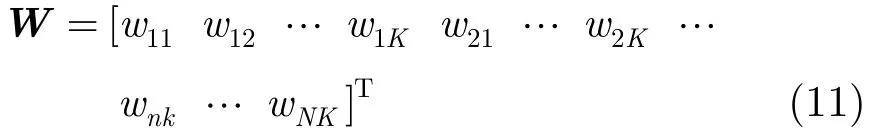
其中,W表示NK×1维的权矢量。R=E[XXH]表示由接收阵列数据形成的NK× NK维协方差矩阵,ST为空时2维导向矢量(NK ×1)。
由式(10),利用拉格朗日乘数法可求得空时2维最优处理器的权矢量Wopt为[20]

如式(6)所示,对于导航信号来说,由于某一时刻的输出是由不同时刻的信号合成的,而不同时刻的信号编码是不一样的,按照传统的空时处理方法必然导致导航信号失真。
如式(7)所示,h=WHS是一矢量,如果把式(10)修改为
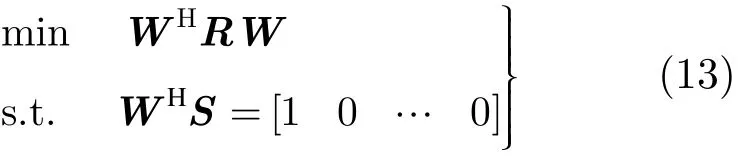
则可以很好解决导航信号失真的问题,此时相当于给延迟信号添加了正交约束,也就是说消除了不同时延信号对最终合成信号的影响,即式(6)的信号输出不包含延时信号:WHSXs=Xs0。这里的S定义同式(3),求出的权值不但可以有效对消干扰,而且把延迟信号对输出的影响进行了过滤。令h= [1 0 … 0],求解式(13),可得最优权值的形式为
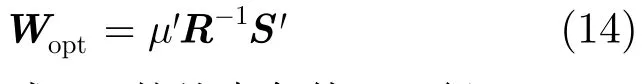
将式(14)代入式(13)的约束条件,可得

式(15)两边右乘HS,并整理可得
此时,可以求得S'为NK×1维矢量
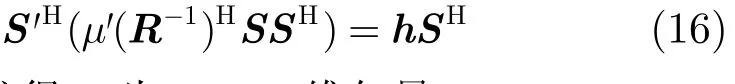
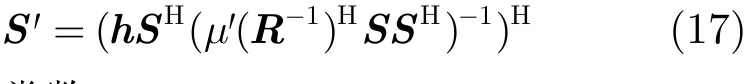
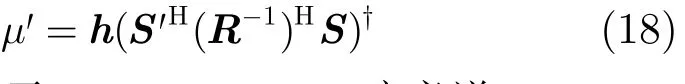
其中,'μ为常数其中,“†”表示Moore-Penrose 广义逆。
从式(17)和式(18)中解出S'是非常困难的,其复杂度也是很高的。但是由于μ'为常数,其对抗干扰效果并无影响,所以计算式(17)时可令μ'=1,另外,由于(μ'(R−1)HSSH)的逆不一定存在,需要对其进行适当的对角加载,这对抗干扰效果影响并不大。
4 仿真实验
本文的仿真主要考察相关峰主瓣的偏移和展宽,仿真参数设置为:卫星信号为C/A码,信噪为-15 dB, 4阵元等距线阵,空时处理的延迟线数为4,采用线性约束最小方差(Linearly Constrained Minimum Variance, LCMV)的单星约束,假定卫星信号来向为0°(阵列法向),干噪比为40 dB,一个宽带压制干扰信号来向为-30°,一个部分带宽干扰(归一化带宽为0.2~0.6,其中整个带宽归一化为-1~1)来向为60°, 3个窄带干扰的来向分别为-45°, 30°和45°,归一化带宽为-0.5, -0.1和0,阵列接受到的信号通过下变频到中频1.023 MHz,采样率为4.092 MHz,载波多普勒频移为2.5 kHz。
实验1 空域处理与空时处理的对比
纯空域处理与空时处理(本文提出基于正交约束的空时处理方法)的比较分为两种情况:情况1是1个宽带干扰加2个窄带干扰加高斯白噪声,干扰数为3;情况2是1个宽带干扰加3个窄带干扰加高斯白噪声,干扰数为4。
图2和图3分别给出情况1的空域处理和基于正交约束的空时处理两种方法的导航信号相关捕获情况。其中图2(a)的3维坐标为多普勒(0~100单元)、码位(0~100单元)和相关值,图2(b)的2维坐标为码位(-5~5,0表示码位刚好对齐)和归一化相关值(0~1.0),图2(b)的2维坐标为多普勒值(2~3 kHz)和归一化相关值(0~1.0),图3,图5~图9,图10和图13的坐标与图2相同,图4、图11和图12的坐标与图2(a)的坐标相同。从图2和图3中可以看出,当干扰数为3时,空域处理和空时处理均可以有效抑制干扰,正常捕获导航信号。
图4和图5分别给出了情况2的空域处理和基于正交约束的空时处理两种方法的导航信号相关捕获情况。从图4和图5中可以看出,当干扰数为4时,空域处理无法有效抑制干扰和捕获导航信号;但是本文所提的基于正交约束的空时自适应处理方法由于抗干扰自由度远大于干扰数,其性能不受影响。
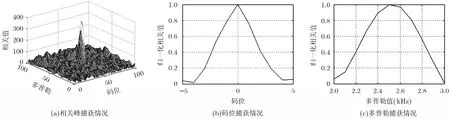
图2 情况1时空域处理
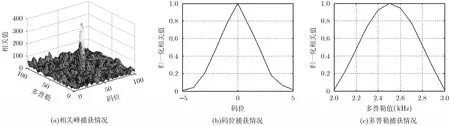
图3 情况1时基于正交约束的空时自适应处理
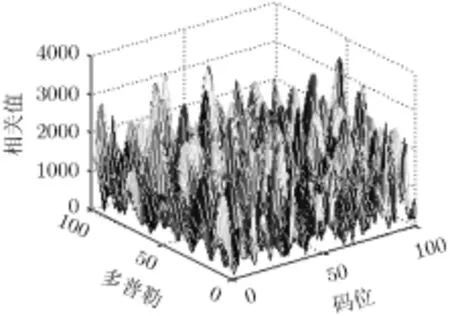
图4 情况2时空域处理
实验2 不同空时处理方法的对比
这里主要是将几种典型的信号失真均衡补偿方法与本文所提方法进行比较,其中方法1表示未经均衡补偿的空时算法,方法2表示文献[4]中所提的均衡补偿方法(Fante补偿方法),方法3表示文献[8]所提的基于逆滤波器的均衡补偿方法,方法4表示本文所提的基于正交约束的空时自适应处理方法。这里的比较也分为两种情况:情况3是只有信号加高斯白噪声,干扰数为0;情况4是信号加一个部分带宽干扰加3个窄带干扰加高斯白噪声,干扰数为4。
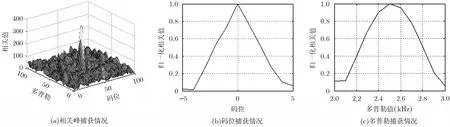
图5 情况2时基于正交约束的空时自适应处理方法
图6~图9分别给出了情况3时未补偿的空时处理、Fante补偿方法、逆滤波器补偿方法和基于正交约束的空时处理方法的相关峰捕获情况。从图中可以看出,当只有信号加高斯白噪声时,未补偿的空时处理方法会导致相关峰偏移,Fante补偿方法则会导致相关峰展宽,并且未补偿和Fante补偿方法的相关峰值很小,逆滤波器方法和基于正交约束的空时自适应处理方法则可以取得满意的结果。
图10~图13分别给出了情况4时4种方法的捕获结果,从图10~图13中可以看出,未补偿的空时自适应处理方法会导致相关峰偏移,且相关峰值很小;Fante补偿方法和逆滤波补偿方法则不能有效捕获导航信号;基于正交约束的空时自适应处理方法则仍然能够得到满意的结果。
5 结论
本文分析介绍了空时自适应处理对导航信号的影响,并基于空时处理导致导航信号失真的机理,从源头上找到了解决传统空时自适应处理导致导航信号失真的方法,提出了基于正交约束的空时自适应处理方法,仿真结果表明,本文所提方法能很好地解决增加抗干扰自由度和信号失真这一对矛盾。相对于补偿方法,本文所提方法更直接、更简洁,效果更好。
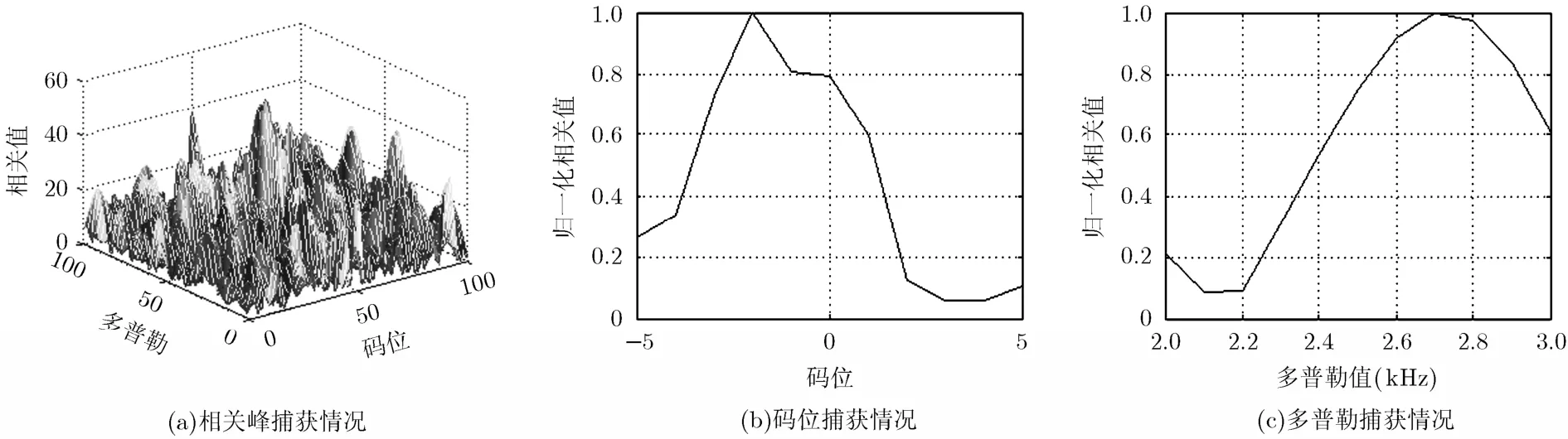
图6 情况.3.时未补偿的空时处理
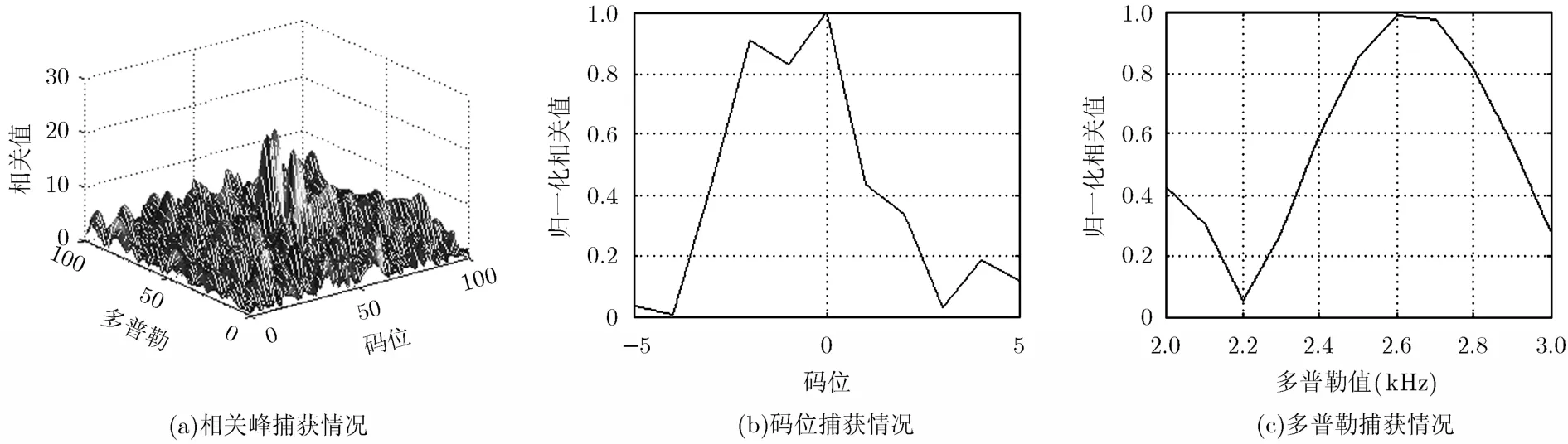
图7 情况.3.时.Fante.补偿方法
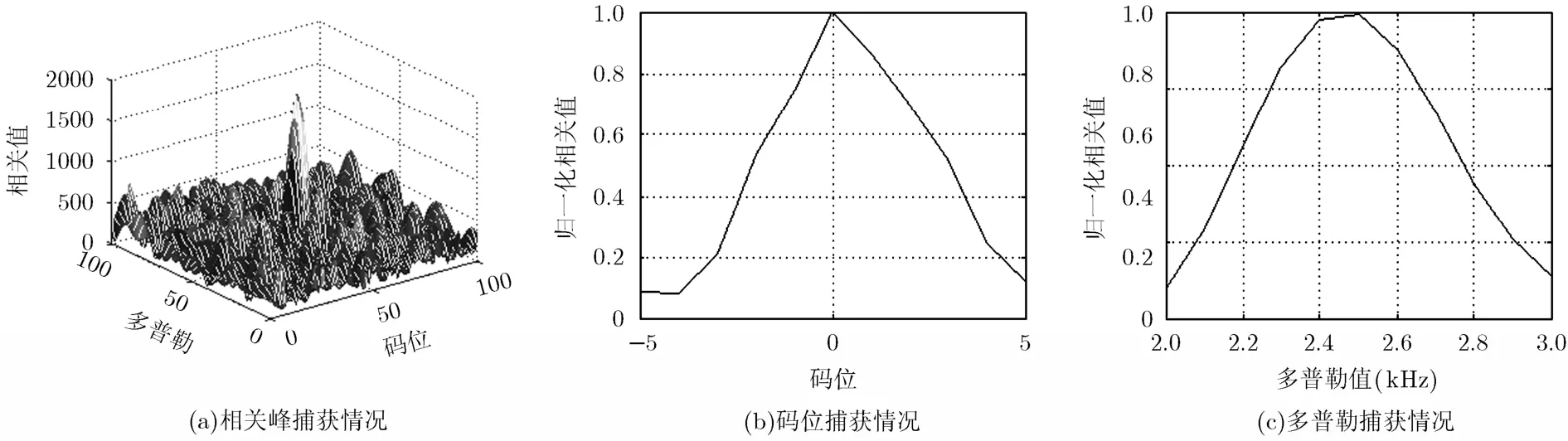
图8 情况.3.时逆滤波补偿方法
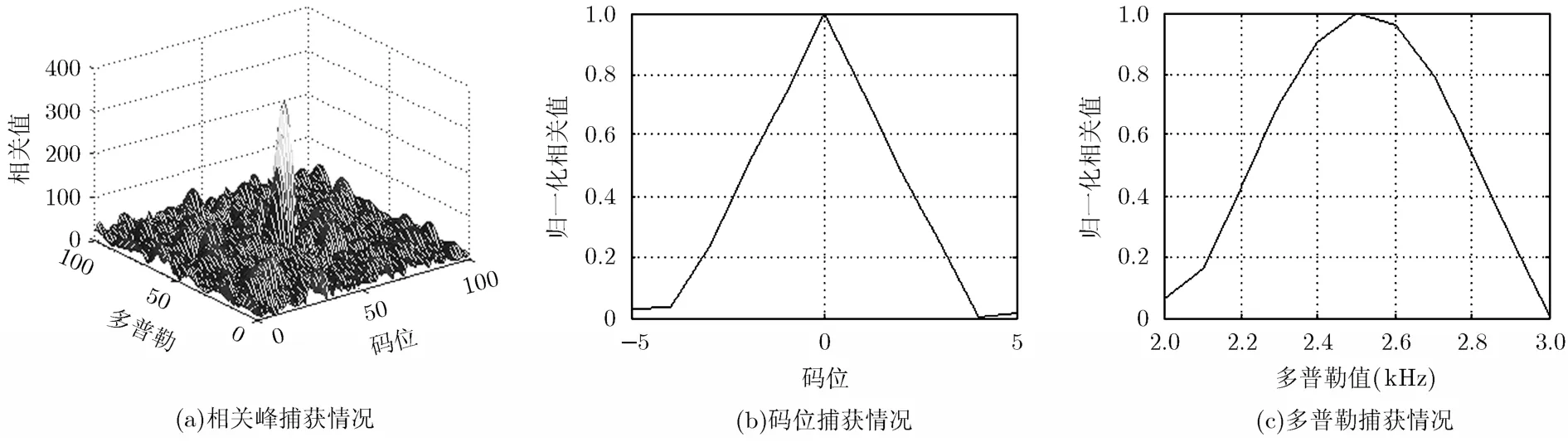
图9 情况.3.时基于正交约束的空时自适应方法
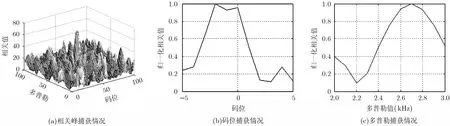
图10 情况.4.时未补偿的空时处理图
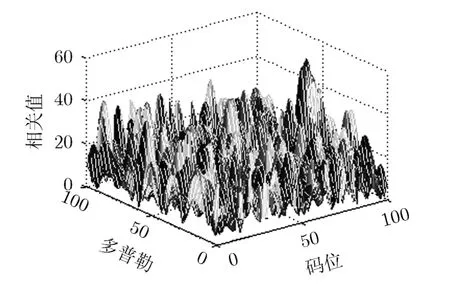
图11 情况.4.时Fante补偿方法图
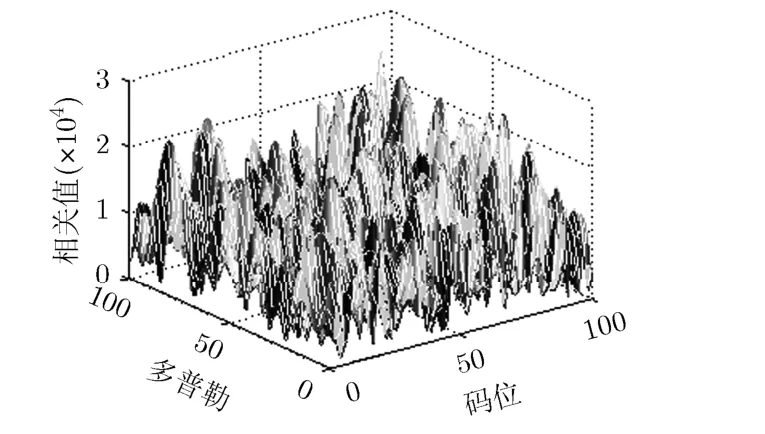
图12 情况.4.时逆滤波补偿方法图

图13 情况.4.时基于正交约束的空时自适应处理方法
[1] 李明峰, 冯宝红, 刘三枝. GPS定位技术及其应用[M]. 北京:国防工业出版社, 2006: 1-17.
Li Ming-feng, Feng Bao-hong, and Liu San-zhi. GPS Positioning Technology and Its Applications[M]. Beijing: National Defense Industry Press, 2006: 1-17.
[2] Jay R S. Interference mitigation approaches for the global positioning system[J]. Lincoln Laboratory Journal, 2003, 14(6): 168-180.
[3] Johan M. Robust navigation with GPS/INS and adaptive beamforming[R]. Scientific Report, Swedish Defence Research Agency Systems Technology Division, 2003.
[4] Cedric Martel. Low profile and anti-jam GPS array[C]. Proceedings of the 2013 IEEE Antennas and Propagation Society International Symposium (APSURSI), Orlando, USA, 2013: 1216-1217.
[5] Zhang Yi-min and Amin M G. Anti-Jamming GPS receiver with reduced phase distortions[J]. IEEE Signal Processing Letters, 2012, 19(10): 635-638.
[6] De Lorenzo D S, Lo S C, et al.. Calibrating adaptive antenna arrays for high-integrity GPS[J]. Springer: GPS Solution, 2012, 16(4): 221-230.
[7] Fante R L and Vaccaro J J. Wideband cancellation of interference in a GPS receive array[J]. IEEE Transactions on Aerospace and Electronic Systems, 2000, 36(2): 549-564.
[8] Fante R L and Vaccaro J J. Cancellation of jammers and jammer multipath in a GPS receiver[J]. IEEE Aerospace and Electronic Systems Magazine, 1998, 13(11): 25-28.
[9] 郭艺. GPS接收机空时抗干扰理论与实现关键技术研究[D]. [博士论文], 长沙: 国防科技大学, 2007. Guo Yi. Research on the theory and key realization technologies of space-time interference suppression for GPS receiver[D]. [Ph.D. dissertation], Changsha: National University of Defense Technology, 2007.
[10] Hatke G F. Adaptive array processing for wideband nulling in GPS system[C]. Proceedings of the 32th Asilomar Conference: Signals, Systems Computers, Pacific Grove, CA, USA, 1998: 1332-1336.
[11] Li S X, Cheng Z, and Huang F K. A compensating approach for signal distortion introduced by STAP[C]. Proceedings of the 2006 ICCT International Conference, Guilin, China, 2006: 1-4.
[12] Wu Ren-biao, Xu Ru-lan, Lu Dan, et al.. STAP compensation technique based on Homomorphic filtering in GPS[C]. Proceedings of the 2010 IEEE International Symposium on Phased Array Systems and Technology (ARRAY), MA, USA, 2010: 841-845.
[13] Fante R L, Fitzgibbons M P, and McDonald K F. Effect of adaptive array processing on GPS signal cross correlation[C]. Proceedings of the 17th International Technical Meeting of the Satellite Division of the Institute of Navigation, California, USA, 2004: 579-583.
[14] Obrien A J and Gupta I J. Mitigation of adaptive antenna induced bias errors in GNSS receivers[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(1): 524-538.
[15] 相飞, 廖桂生, 曾操. 空时自适应处理对GPS信号影响与补偿方法[J]. 系统工程与电子技术, 2012, 34(1): 1-6.
Xiang Fei, Liao Gui-sheng, and Zeng Cao. Effect of spacetime adaptive processing on GPS signals and its compensation method[J]. Systems Engineering and Electronics, 2012, 34(1): 1-6.
[16] Ren Chao, Wang Yong-qing, and Zhou Shan. Wideband interference suppression based on space-time filter[J]. Journal of Beijing Institute of Technology, 2013, 22(1): 67-74.
[17] Zhao Yun, Xue Xiao-nan, and Zhang Ting-fei. Receiverchannel based adaptive blind equalization approach for GPS dynamic multipath mitigation[J]. Chinese Journal of Aeronautics, 2013, 26(2): 378-384.
[18] Xiong Tao, Zhang Shun-sheng, and He Ming-dong. Antijamming performance evaluation based on GPS software receiver[C]. Proceedings of the 2013 International Workshop on Microwave and Millimeter Wave Circuits and System Technology, Chengdu, China, 2013: 407-410.
[19] Qiang Li, Wei Wang, Dingjie Xu, et al.. A robust anti
jamming navigation receiver with antenna array and GPS/SINS[J]. IEEE Communications Letters, 2014, 18(3): 467-470.
[20] 王永良, 彭应宁. 空时自适应信号处理[M]. 北京: 清华大学出版社, 2000: 46-57.
Wang Yong-liang and Peng Ying-ning. Space-Time Adaptive Processing[M]. Beijing: Tsinghua University Press, 2000: 46-57.
张柏华: 男,1979年生,博士,博士后,研究方向为雷达、导航、阵列信号处理.
马红光: 男,1959年生,博士,教授,研究方向为雷达、信号处理、非线性系统等.
孙新利: 男,1963年生,博士,教授,研究方向为卫星导航、信号处理、战斗部可靠性等.
Space Time Adaptive Processing Technique Based on Orthogonal Constraint in Navigation Receiver
Zhang Bai-hua①②Ma Hong-guang①Sun Xin-li①Tan Qiao-ying③Pan Han-jin④
①(The Second Artillery Engineering University, Xi'an 710025, China)
②(No. 95100 Unit of Air Force, Guangzhou 510405, China)
③(Motorcycle Test Technology Institute of China South Industries Group Corporation, Xi'an 710032, China)
④(The Army Aviation Research Institute of Headquarters of General Staff, Beijing 101121, China)
Satellite navigation systems is susceptible to jamming, Space-Time Adaptive Processing (STAP) technique has obvious advantage in the anti-jamming of navigation receiver, i.e. system Degree Of Freedom (DOF) visibly increasing, but traditional STAP would bring serious signal distortion in navigation receiver anti-jamming. In this paper, a novel STAP method based on orthogonal constraint in navigation receiver is proposed. This method modifies the constraint of traditional STAP based on the principle of STAP, avoids the influence of the delay time signal, the jamming is efficiently suppressed by STAP in the acquisition and decoding of navigation signal. Theory analysis and simulation indicate that the novel technique can solve the problem of navigation signal distortion in STAP efficiently.
Satellite navigation systems; Orthogonal constraint; Navigation receiver; Signal distortion; Space Time Adaptive Processing (STAP); Anti-jamming
TN967.1
: A
:1009-5896(2015)04-0900-07
10.11999/JEIT140740
2014-06-03收到,2014-09-11改回
国家部级基金资助课题
*通信作者:张柏华 berlainzbh2001@aliyun.com

