基于自适应超时计数布鲁姆过滤器的流量测量算法

侯 颖黄 海 兰巨龙 李 鹏 朱圣平

(国家数字交换系统工程技术研究中心 郑州 450002)

基于自适应超时计数布鲁姆过滤器的流量测量算法

侯 颖*黄 海 兰巨龙 李 鹏 朱圣平

(国家数字交换系统工程技术研究中心 郑州 450002)

针对流量测量中IP长流的检测问题，该文设计了计数布鲁姆过滤器(Count Bloom Filter, CBF)与超时布鲁姆过滤器(Timeout Bloom Filter, TBF)结合的长流检测机制。该机制动态调整布鲁姆过滤器中的超时时间，及时清理结束流，解决空间拥塞问题，从而可以适用于无结束标志IP长流检测。依据算法整体错误率与超时时间的分析，根据链路流到达强度与布鲁姆过滤器向量空间长度自适应动态调整超时时间，使得算法整体错误率保持最低。该算法的性能利用真实网络流量数据进行验证，结果表明，与现有算法相比，该算法的测量准确性更高。

网络测量；流量测量；长流；动态调整

1 引言

流量测量是互联网研究的重要领域，是网络体系研究、网络异常检测和服务质量(Quality of Service, QoS)管理的基础[1,2]。目前对互联网流量进行测量多以流为基本单元，即具有相同五元组(源目IP地址、源目端口号和协议类型)的数据分组集合。随着网络链路带宽的增加，在高速网络环境中并发网络流巨大，难以缓存所有流信息进行流量测量[3]。在诸如大规模网络安全事件等应用中，只关注网络中的大流量对象。因此长流检测算法，也称为大流检测算法，成为网络测量领域研究的热点之一[4]。

本文中的长流是指在一定的测量时间段内流大小达到或超过阈值的流。当前主要的长流检测方法可以分为3类：概率抽样方法、流链表方法和计数布鲁姆过滤器(Count Bloom Filter, CBF)方法。

代表性的概率抽样方法为Estan等人[5]提出的抽样保持(Sample and Hold, SH)算法，其基本思想为：当某个数据报文到达时，如果该报文所属的流已被抽中，则更新该流记录；否则以一定概率p采样该报文。该方法实现简单，但是单纯以概率p进行抽样，误差较大。

在流链表方法上，文献[6]中提出将最近最久未使用(Least Recently Used, LRU)算法应用到长流检测中，算法的核心思想是：在有新流到达时，将最久未有报文的流替换出去，该算法只需维护链路中活跃流状态，不用定时扫描流表，将已结束流释放，减少了系统开销。LRU算法有很多改进方案：文献[7]提出基于LRU和布鲁姆过滤器(Bloom Filter, BF)的长流检测机制，将长流过滤和长流判断分离，进一步降低了长流淘汰的错误概率；文献[8]提出基于流更新频率和大小的大流检测算法(Flow Extracting with Frequency & Size, FEFS)，在链表中通过淘汰小流来保存和更新大流信息。流链表方法为了定位流表，需要保留每个流的五元组信息，占用空间较大，而且通过哈希函数定位流表，哈希冲突时需顺序查询冲突链表，开销较高。

CBF方法由于实现结构简单，易于硬件实现，在长流检测算法中一直被广泛应用。最初的CBF长流检测算法为文献[5]提出的多级过滤器算法(Multistage Filters, MF)，该算法应用多个哈希空间对流的报文进行计数，如果每个哈希空间相应的流计数器都超过了预设定的阈值，则认为该流是长流。文献[9]提出基于多粒度计数布鲁姆过滤器的长流识别算法，采用空间大小递减的多个CBF对流长度进行计数，算法所需存储空间相对传统流表方法和CBF方法都有所减少。文献[10]提出基于双重计数布鲁姆过滤器进行长流识别和抽样，将长流过滤和长流存在分开进行处理，与MF算法相比，具有更高的准确度。

基于CBF的长流检测算法存在空间拥塞问题。对于TCP流，通过报文的FIN/RST等标志判断流结束，可以将流占用的计数器清除。但是网络链路中还存在大量无结束标志的IP流，如SYN攻击报文、路由变化等原因产生的无结束标志TCP流，以及占网络流量比重越来越多的UDP流[11]等。因此，对于这些无结束标志的IP流，如何判断流结束，并及时将这些已终结流对应的计数器清除，是CBF方法面临的难题。文献[9]中采用定时更新方法，定时清除CBF中占用的计数器空间。但定时更新方法割裂了定时时刻前后两个时间段流之间的关系，容易导致测量误差。此外每次定时更新都需要检测所有计数器空间，额外增加了处理开销，尤其当计数器空间较大时，定时更新的开销对测量系统性能影响较大。

在流量测量领域，一些研究关注如何通过合理的超时机制将结束的数据流资源及时释放。文献[12]采用固定64 s超时机制对流结束进行判断，并通过实验验证该方法在大部分情况下具有较好的效果。但64 s超时只是对大部分流有效，部分慢流还是会被截断为多流，导致系统产生误判。文献[13]提出二进制指数超时(Measurement-based Binary Exponential Timeout, MBET)的流超时算法，根据每个流的数据报文吞吐量、报文间隔等信息动态调整超时时间，实现尽快将已结束流资源释放。文献[14]提出了一种基于流速测度的动态超时策略，对长流和短流采用不同的超时策略和预制。文献[15]提出了针对不同长度的UDP流采用不同超时方式的超时策略：对单报文流采用空间受限方式淘汰过期流，对短流采用MBET策略淘汰过期流，对于长流采用预测包间隔方法来设置流超时值。这3种方法均需要利用流的历史信息计算流的流量特性，因此难以在CBF结构上应用。文献[16]提出了超时布鲁姆过滤器(Timeout Bloom Filter, TBF)进行包抽样的方法，其原理是：在布鲁姆过滤器向量中保存旧报文到达的时间戳，根据新报文到达时间戳是否超时，判断报文是否属于需要抽样的新流，避免了布鲁姆过滤器空间拥塞导致的误判问题。

本文基于CBF和TBF的思想，设计了适用于检测无结束标志IP长流的超时计数布鲁姆过滤器(Count Timeout Bloom Filter, CTBF)结构，该结构由计数器向量和计时器向量组成，一方面通过计数器向量记录IP流的报文数量判断长流，另一方面通过计时器向量记录IP流最后报文的到达时刻，及时将已终结流占用的计数器自动清除，解决了无结束标志IP流导致的布鲁姆过滤器空间拥塞问题；分析了CTBF长流检测结构的误差与计时器超时时间的关系，在此基础上提出了自适应超时计数布鲁姆过滤器(Adaptive Count Timeout Bloom Filter, ACTBF)长流检测算法，根据链路流到达强度与布鲁姆过滤器向量空间长度自适应调整超时时间，使得算法的整体错误率始终保持在较优范围。本文后续部分组织如下: 第2节是自适应超时的CTBF长流检测算法的设计与分析；第3节通过实验对算法进行了验证；第4节是本文的总结。

2 自适应超时的CTBF长流检测算法

2.1 CTBF长流检测结构

CTBF结构由k个独立的哈希函数h1,h2,…,hk以及长度均为m的两个向量Vc和Vt组成。每个哈希函数相互独立且函数取值范围为{1,2,…,m}。向量Vc的每一维设置成一个计数器，记为c(i)，初值设为0，记录流报文计数。向量Vt的每一维设置成一个计时器，记为t(i)，初值设为当前时刻，记录最近报文的时间戳。

CTBF结构的长流检测原理为：对于流集合S={s1,s2,…,sn}中的任一元素si，通过k个哈希函数得到k个取值范围为[1,m]之间的值，从而映射到向量Vc和Vt的k个存储单元，分别进行更新。计数器向量Vc的更新操作是把k个存储单元的计数器加1，并判断是否超过长流阈值。计时器向量Vt的更新操作是把k个存储单元的时间戳更新为当前时间戳，并判断k个存储单元原先保留的时间戳与当前时间戳的差值是否超过设定的超时门限，如果超过则判断为新流，并清除计数器向量Vc对应的存储单元。因此，通过计时器向量Vt进行更新操作，CTBF结构即可将已终结流占用的计数器自动清除，节省了处理开销。

假设N为长流报文阈值，T为预设的流报文超时时间，CTBF算法的主要过程是：

(1)设一个报文在t时刻到达，提取流标识s(源IP地址、源端口号、目的IP地址、目的端口号、协议类型)作为哈希函数的输入，得到k个哈希值hj(s)，且1≤j≤k；

(2)计算报文间隔时间Δtj，其中Δtj=t -t(hj(s))，且1≤j≤k；

(3)更新向量Vt中计时器t(hj(s))=t；

(4)如果存在Δtj≥T，则认为此报文为新流的首报文，更新向量Vc中计数器c(hi(s))=1，其中i取值满足Δtj≥T，且1≤j≤k；

(5)如果对于任意j(1≤j≤k)，均有Δtj≤T成立，则认为此报文所属流已存在，更新向量Vc中计数器c(hj(s))=c(hj(s))+1，取cmin=min(c(hj(s)))，如果cmin＞N，标记该流为长流。

图1为t时刻收到报文为新流首报文和旧流中间报文时CTBF结构的处理示意图。图1(a)为收到新流首报文时，CTBF结构向量Vc和Vt存储单元的变化示意，其中哈希函数个数k=3，流对应的哈希值分别为1,2,m−1，当前时间戳为t。收到该报文后，向量Vt对应的计时器均更新为t，由于只有t1计时器超时，向量Vc只有c(1)数值变为1，其他存储单元不变。图1(b)为收到旧流中间报文时，CTBF结构向量Vc和Vt存储单元的变化示意，流对应的哈希值分别为1,2,m−1，当前时间戳为t，没有计时器超时。收到该报文后，向量Vt对应的计时器均更新为t，由于没有计时器超时，向量Vc对应的计数器均加1。

2.2 CTBF长流检测结构误差分析

基于CTBF结构进行长流检测的误差主要由两部分组成：一方面，CTBF结构通过多个哈希函数降低哈希映射冲突的概率，但依然会存在“假阳性误判”，使得部分短流因为哈希冲突误判为长流；另一方面，超时机制难以避免会将慢的长流截断为多个流，从而导致长流被误判为短流或长流的流长统计出现错误。

2.2.1 超时时间与布鲁姆过滤器误判的关系 布鲁姆过滤器的误判可以表达为：当新流到达时，在向量Vt中，由k个哈希函数计算的k个时间戳均未超时，这种情况下新流会被误判为已存在的活跃流，从而产生错误判断。

假设网络中有n个活跃流，向量Vt长度为m，由于活跃流对应的向量Vt中的k×n个时间戳均被及时更新，则向量Vt中某个时间戳判断为超时的概率为

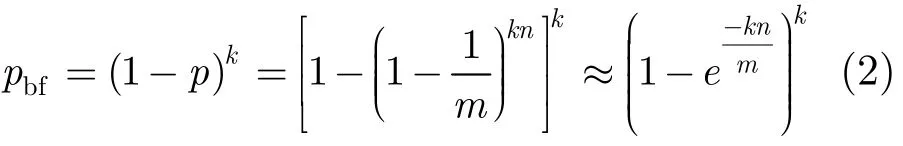
而新流被误判的前提是其对应的k个时间戳值均未超时，因此新流被误判概率为

由式(2)可知，在向量Vt长度m和哈希函数k固定的情况下，算法误判率与网络中活跃流数量n正相关。对于CTBF结构，已经结束但没有达到超时阈值的流都被认为是活跃流，因此CTBF结构下活跃流数量n与算法的超时阈值T相关。

定理1 设网络链路中流到达服从强度为λ的泊松分布，流实际结束过程服从参数为μ的指数分布，T为流结束后的超时阈值，则稳态下系统测量的平均流数量EX可以表示为：EX=λT+λ/μ。

证明 由于流到达过程为泊松过程，其到达间隔时间序列记为S ={Sk,k ≥0}，设超时时间T对应的时间序列下标k=t，则超时时间T以后流到达间隔时间序列是S的子集，记为S'={Sk+t,k ≥0},S'服从以λ为参数的指数分布。

由于流的结束过程服从指数分布，其持续时间序列记为B ={Bk,k ≥1},B服从以μ为参数的指数分布。

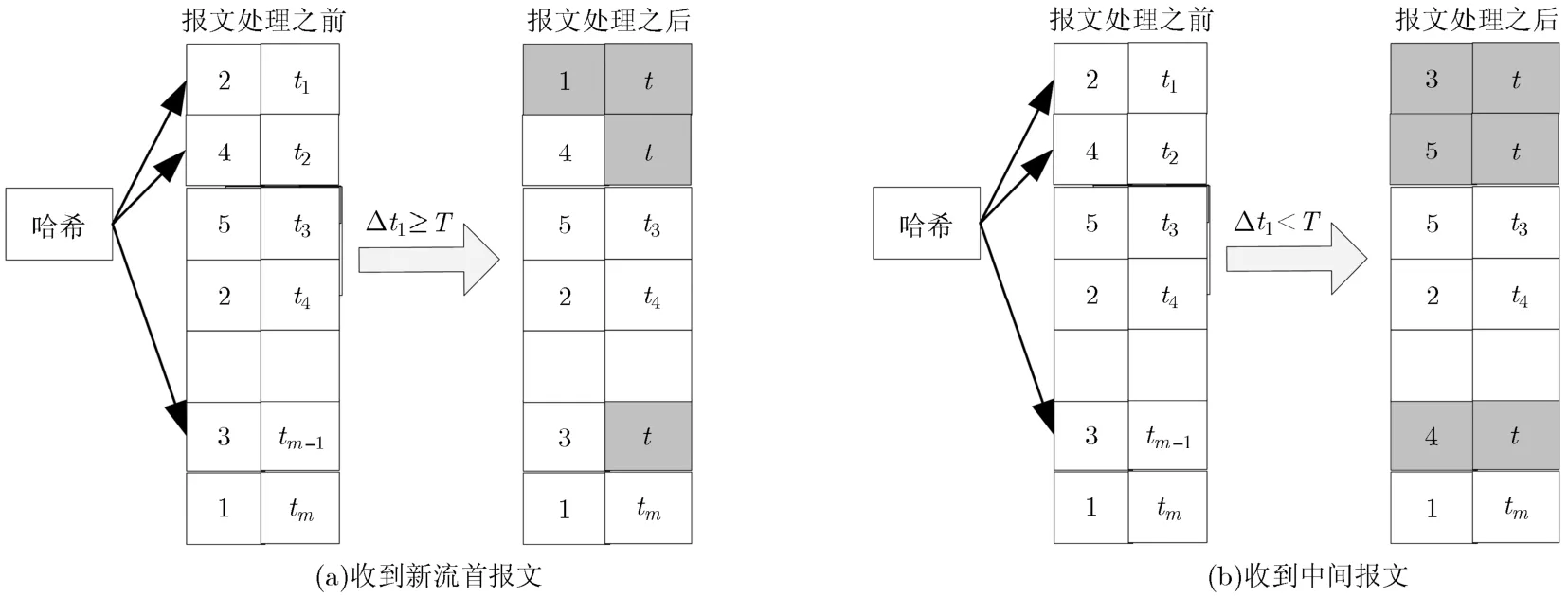
图1 t时刻收到新流首报文和中间报文时CTBF处理示意图

设X ={X(t),t≥0}为时刻t+T时系统测量的网络流数量，XT为T时刻到达的网络流数量，则记X'={X(t)−XT,t ≥0}。

根据生灭过程的性质，其平稳分布存在，可表示为

显然，X'(t)为生灭过程，其出生率和死亡率分别为

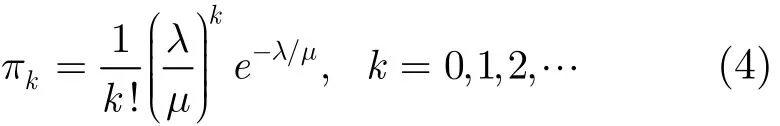
因此可得X(t)稳态下的均值

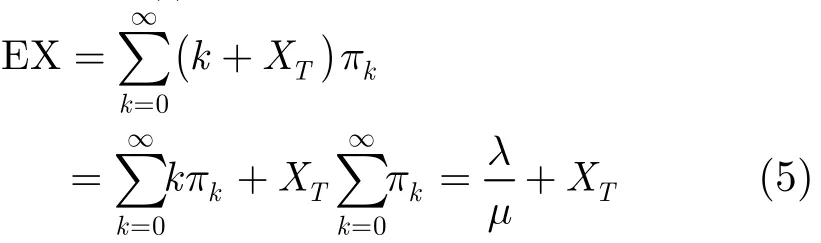
由于流到达过程为泊松过程，T时刻的到达的网络流平均数量为λT，因此有

证毕

将式(6)代入式(2)，可得布鲁姆过滤器的误判率为

记θ=λ/m，由于1/μ≪T，因此式(7)可以表示为

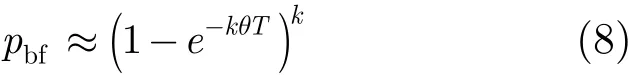
定义1 空间充满速率θ为网络链路流到达强度λ与向量空间长度m的比值。其物理含义为，在不考虑流结束情况下，一个空的布鲁姆过滤器向量空间被占满的速率。

设定哈希函数个数k为4，向量长度m为107，网络链路流到达强度λ=2000，即θ为1/500时，根据上式仿真了超时阈值与布鲁姆过滤器的误判率的关系曲线，如图2所示。从图中可以看出，随着超时阈值增加，布鲁姆过滤器误判率增加，超时阈值越小误判率下降速度越快。

2.2.2 超时时间与长流截断概率的关系 对网络中的流报文到达间隔的研究发现：随着报文到达时间的增加，在指定时段内到达报文的数量逐渐减小，而且报文数减小的幅度也逐渐减小[14]。这说明随着超时时间增加，流截断概率逐渐减少，而且其减少的幅度也不断减少。本节通过网络真实流量数据，分析了超时时间与长流截断概率的关系。流量数据选自美国国家实验室 NLANR 公开的被动型测量数据，数据源文件为ERF格式[17]，流量数据分别采自Waikato大学校园网和新西兰的某个ISP，为保护用户隐私，流量数据中仅仅包含数据报文的头部。

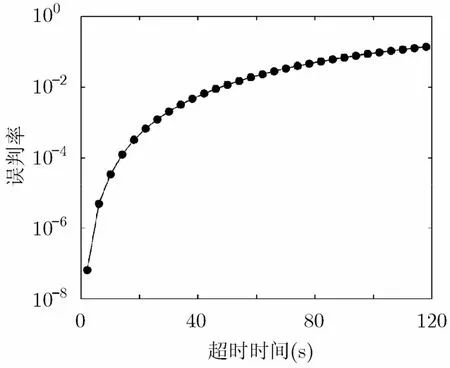
图2 超时阈值与布鲁姆过滤器误判率的关系

实验方法为统计数据集中每流的最大报文间隔，如果流的最大报文间隔大于超时时间T，则认为该流在超时时间T时被截断。图3列出了数据集中报文数大于20, 50和100的长流截断概率与超时时间的关系。横坐标为超时时间，图3(a), 3(c)纵坐标为截断概率，图3(b), 3(d)纵坐标为截断概率的自然对数。从图中可以看出，流截断概率为超时时间的负指数函数，并且报文数大于20, 50和100的流的截断概率曲线基本重合。以新西兰ISP数据集为例，在超时时间为200 s时截断概率取值约为2.4%，在100 s时取值约为9.2%，在64 s时取值约为15.1%。根据这一分析，采用文献[12]的固定64 s超时机制，高达15.1%的长流会被截断。

通过图3(b), 3(d)超时时间与截断概率的自然对数关系曲线图可以看出，截断概率的自然对数与超时时间的图形为多折线，整体上流截断概率是超时时间的负指数函数，可以表示为

其中β代表了截断概率随超时时间的下降速度。利用不同的β，图3(b), 3(d)中对报文数＞100的截断概率曲线按式(9)进行了分段拟合，拟合曲线与实际曲线基本重合。

2.2.3 整体错误率分析 根据上面分析，CTBF结构的整体错误率可以表示为

令f(T)=(1−e−kθT)k+αe−βT，则其一阶导数为

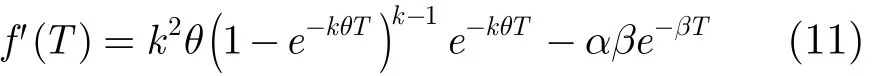
当kθT远小于1，根据麦克劳林公式，式(11)可以表示为

图3 超时时间与流截断概率的关系

当T使得f′(T)等于0时，即T满足式(13)时，f(T)存在极值。

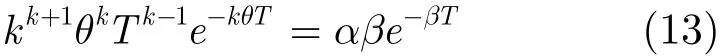
转换后可得

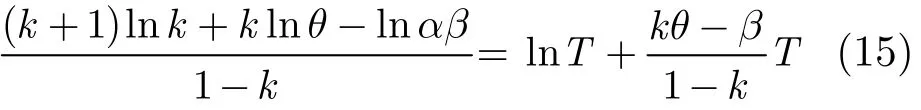
两边取自然对数后，可得则式(15)可以简化为：c=lnT+bT 。两边取自然指数得：ec=TebT；两边同时乘以b，可得形同朗科函数的方程：bec=bTebT。根据朗科函数定义，方程解形式为

其中W(x)为朗科函数。因此，当T=W(bec)/b 时，函数f(T)有极值，不难验证该值为极小值。当哈希函数个数k为4, CTBF结构的整体错误率与超时时间T的关系曲线如图4所示。

从图4可以看出，当超时时间较小时，会导致长流被截断，由此产生错判，随着超时时间增加，长流截断造成的错判减少，但是由于CTBF结构中活跃流数量增多，使得布鲁姆过滤器空间占用率上升，导致误判升高，算法存在最优的超时时间，使得算法的整体错误率最低。

另外随着空间充满速率θ的下降，算法的最优超时时间也逐步变大，而且算法的整体错误率也降低。其原因在于随着θ下降，布鲁姆空间的占用率较低，由于布鲁姆过滤器误判造成的错误比重减小，算法可以使用较大的超时时间减少长流被截断的影响。

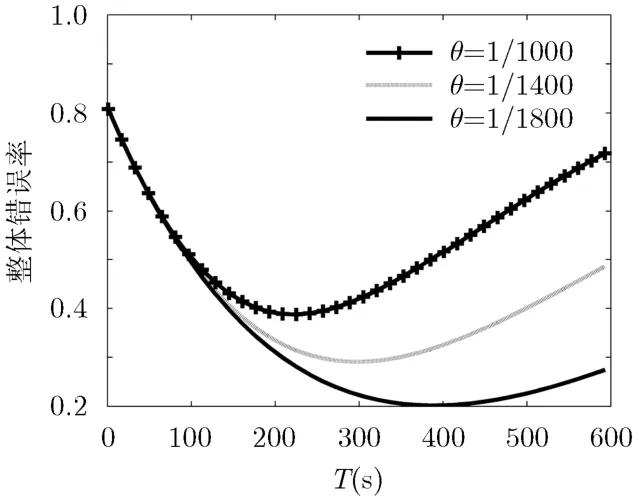
图4 CTBF整体错误率与超时时间的关系

2.3 自适应超时机制

根据2.2节分析，CTBF长流检测算法存在使得整体错误率最低的最优超时时间，该超时时间与空间充满速率θ，即链路中流量到达速率和布鲁姆过滤向量长度相关。为此，提出基于自适应超时机制的ACTBF算法，根据当前链路中流到达强度λ与向量空间长度m，计算测量系统当前时刻的空间充满速率θ，从而得出当前时刻使得长流检测整体错误率最低的超时时间T，使得算法的整体错误率始终保持在较优范围。

计算最优超时时间涉及对数计算、求解朗科函数等较复杂的数学运算，在测量系统中实时求解会影响系统处理速度。在实际应用中，可以对空间充满速率θ设定有限个取值区段，预先计算对应θ区段的最优超时时间T，通过查表方式获得当前θ对应的近似最优超时时间T。

3 算法验证

本文选择2.2节的数据集对ACTBF算法的长流检测准确率进行验证。两个数据集的流到达速率λ如图5(a), 5(b)所示。当k=4，布鲁姆过滤器向量长度m为106时，对应的最优超时时间T变化情况如图5(c), 5(d)所示。可以看出ISP数据集的流到达速率λ主要在1000～1500之间波动，Waikato校园网数据集的流到达速率λ相对较小，主要在500～1000之间波动。但是Waikato数据集在时间为210 s, 563 s和672 s时刻出现突发流量，在210 s处流到达速率为2632，达到平均流速的一倍，其对应的最优超时时间T也相应变小。

设置哈希函数k=4，长流检测阈值N=100，在布鲁姆过滤器向量长度为106时，ACTBF算法与固定超时CTBF算法的准确率进行测试，结果如图6所示，横坐标为固定超时算法设置的超时时间，范围为从48 s到384 s，纵坐标为长流误判概率。对于固定超时CTBF算法，随着超时时间的增加，长流检测错误率先下降然后再逐渐升高，而ACTBF无需设置超时时间，其检测错误率为固定值。

由于目前的基于CBF结构的长流检测算法，如MF, CCBF等，都只能检测有结束标志的TCP长流，只有LRU类长流检测算法能够适用于检测UDP长流或无结束标志的TCP长流。因此，本文选择LRU, LRU-BF与ACTBF算法，在占用相同内存空间的条件下进行实验。数据源选择New Zealand ISP数据，哈希函数k=4，长流检测阈值N=100, LRU算法中单流记录占用空间为22 Byte(五元组13 Byte、报文计数1 Byte、双向链表指针8 Byte)。算法的错误率比较结果如图7所示。从图中可以看出，在占用相同的存储空间条件下，ACTBF算法的准确率高于LRU和LRU-BF算法，这是因为LRU类算法需要存储流的五元组和链表指针等信息，在相同存储空间下其可存放的流表记录大幅度减少，导致流反复被淘汰，影响了准确率。从图7也可以看出，同样错误率条件下，ACTBF比LRU算法所需内存空间都少，当错误率为1%时，ACTBF, LRUBF和LRU对应的内存占用分别为6 MB, 11 MB和21 MB。与LRU算法相比，由于ACTB算法需要计算k个哈希函数值，因此当k取值较大时，影响算法处理速度。但是ACTBF算法逻辑相对简单，在实际系统设计时，可以将哈希函数采用硬件实现并行处理，提高处理速度。

4 结束语

在实际网络链路中，流量到达强度及长度分布复杂多变，根据流量的变化，自适应调整相关参数的大流识别方法具有重要意义[4]。本文提出一种适合在高速网络中检测无结束标志IP长流的ACTBF长流检测算法。算法设计基于两个布鲁姆过滤器组合结构：计数布鲁姆过滤器，实现了流的高效报文计数，节省了存储空间；超时布鲁姆过滤器及时释放已结束的流占用的空间。超时布鲁姆过滤器中超时时间根据链路流到达强度与布鲁姆过滤器向量空间长度自适应动态调整，使得算法整体错误率始终保持最低。

本文利用真实互联网流量数据集对算法进行了实验验证，实验结果表明：固定超时CTBF算法的错误率随流量的到达速率波动较大，而动态调整超时时间的ACTBF的错误率较稳定，并且性能优于固定超时CTBF算法的最优值。与LRU和LRU-BF算法的比较说明，在同等条件下，ACTBF算法的准确率更高。

[1] 兰巨龙, 程东年, 胡宇翔. 可重构信息通信基础网络体系研究[J]. 通信学报, 2014, 1(1): 128-139.

图5 测试数据集流到达速率以及算法超时时间的变化情况

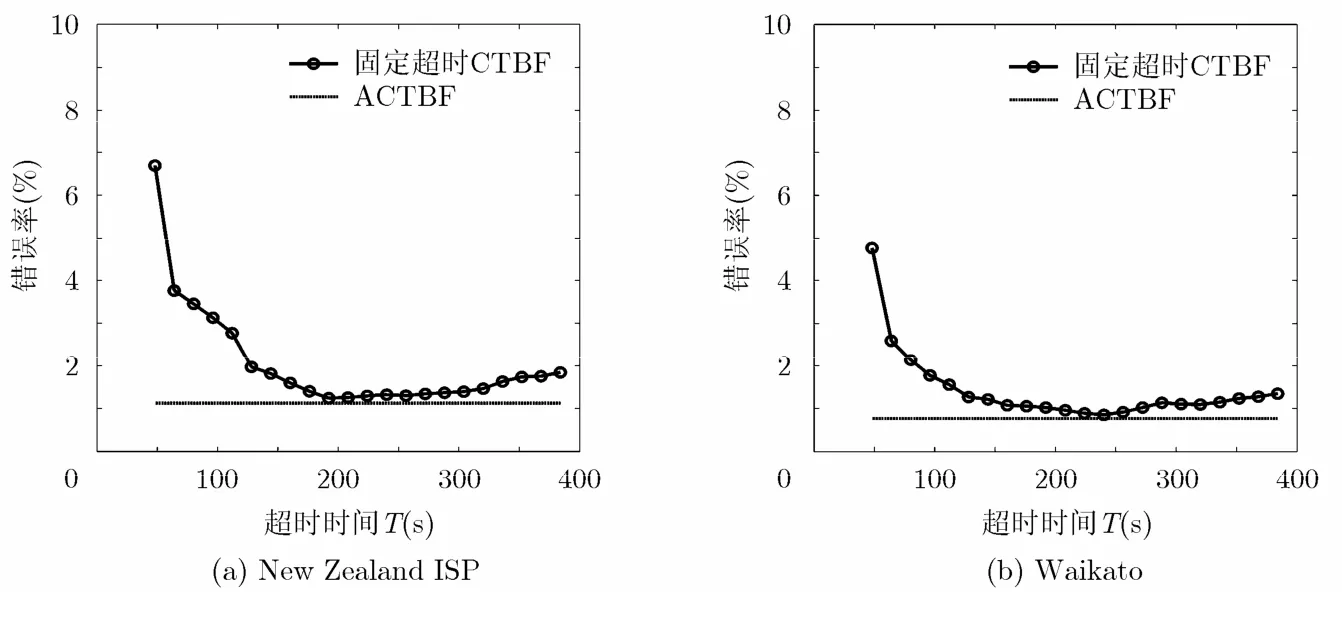
图6 固定超时CTBF算法与ACTBF算法的准确率比较

图7 占用相同内存情况下ACTBF 算法与LRU类算法的比较

Lan Ju-long, Cheng Dong-nian, and Hu Yu-xiang. Research on reconfigurable information communication basal network architecture[J]. Journal on Communications, 2014, 1(1): 128-139.

[2] He Ke-qiang, Hu Cheng-chen, Jiang Jun-chen, et al.. Anti-attack counters for traffic measurement[C]. Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM 2010), Miami, USA, 2010: 1-5.

[3] 周爱平, 程光, 郭晓军. 高速网络流量测量方法. 软件学报[J]. 2014, 25(1): 135-153.

Zhou Ai-ping, Cheng Guang, and Guo Xiao-jun. High-speed network traffic measurement method[J]. Journal of Software, 2014, 25(1): 135-153.

[4] 夏靖波, 任高明. 大流识别方法综述[J]. 控制与决策, 2013, 28(6): 801-807. Xia Jing-bo and Ren Gao-ming. Survey on elephant flow identifying methods[J]. Control and Decision, 2013, 28(6): 801-807.

[5] Estan C and Varghese G. New directions in traffic measurement and accounting: focusing on elephants, ignoring the mice[J]. ACM Transactions on Computer Systems, 2003, 21(3): 270-313.

[6] 王洪波, 裴育杰, 林宇, 等. 基于LRU的大流检测算法[J]. 电子与信息学报, 2007, 29(10): 2487-2492.

[7] 张震, 汪斌强, 张风雨, 等. 基于LRU-BF策略的网络流量测量算法[J]. 通信学报, 2013, 34(1): 111-120.

Zhang Zhen, Wang Bin-qiang, Zhang Feng-yu, et al.. Traffic measurement algorithm based on least recent used and Bloom filter[J]. Journal on Communications, 2013, 34(1): 111-120.

[8] 王风宇, 郭山清, 李亮雄, 等. 一种高效率的大流提取方法[J].计算机研究与发展, 2013, 50(4): 731-740.

Wang Feng-yu, Guo Shan-qing, Li Liang-xiong, et al.. A method of extracting heavy-hitter flows efficiently[J]. Journal of Computer Research and Development, 2013, 50(4): 731-740.

[9] 周明中, 龚俭, 丁伟, 等. 基于MGCBF算法的长流信息统计[J]. 东南大学学报(自然科学版), 2006, 36(3): 472-476.

[10] 吴桦, 龚俭, 杨望. 一种基于双重Counter Bloom Filter的长流识别算法[J]. 软件学报, 2010, 21(5): 1115-1126.

[11] Zhang M, Dusi M, John W, et al.. Analysis of udp traffic usage on internet backbone links[C]. Proceedings of 9th Annual International Symposium on Applications and the Internet(SAINT 2009), Seattle, USA, 2009: 280-281.

[12] Claffy K C, Braun H W, and Polyzos G C. A parameterizable methodology for Internet traffic flow profiling[J]. IEEE Journal on Communications, 1995, 13(8): 1481-1494.

[13] Ryu B, Cheney D, and Braun H W. Internet flow characterization: adaptive timeout strategy and statistical modeling[C]. Proceedings of Passive and Active Measurements, Amsterdam, Netherlands, 2001: 94-105.

[14] 周明中, 龚俭, 丁伟. 高速网络中基于流速测度的动态超时策略[J]. 软件学报, 2005, 16(5): 562-568.

[15] 赵小欢, 夏靖波, 朱长虹. 高速网络 UDP 流超时策略研究[J]. 合肥工业大学学报(自然科学版), 2013, 36(2): 176-180.

Zhao Xiao-huan, Xia Jing-bo, and Zhu Chang-hong. Research on UDP flow timeout strategy in high-speed network[J]. Journal of Hefei University of Technology (Natural Science Edition), 2013, 36(2): 176-180.

[16] Kong S, He T, Shao X, et al.. Time-out bloom filter: a new sampling method for recording more flows[C]. Proceedings of the International Conference on Information Networking (ICOIN 2006), Sendai, Japan, 2006: 590-599.

[17] NLANR. National Laboratory for Applied Network Research [OL]. http://pma.nlanr.net/.2014. 04

侯 颖： 女，1973年生，副研究员，研究方向为网络测量和网络信息安全.

黄 海： 男，1975年生，副教授，研究方向为网络体系结构和网络信息安全.

兰巨龙： 男，1962年生，教授，研究方向为网络体系结构和路由交换技术.

李 鹏： 男，1978年生，工程师，研究方向为网络流量测量.

朱圣平： 男，1967年生，工程师，研究方向为网络管理.

An Adaptive Timeout Counter Bloom Filter Algorithm for Traffic Measurement

Hou Ying Huang Hai Lan Ju-long Li Peng Zhu Sheng-ping
(National Digital Switching System Engineering & Technological R&D Center, Zhengzhou 450002, China)

A novel mechanism combining Counting Bloom Filter (CBF) and Timeout Bloom Filter (TBF) is proposed, aiming at identifying IP long flow precisely. By adjusting the timeout dynamically and deleting end flows timely, the mechanism can solve the space congestion of Bloom filter and identify heavy hitters without normal end flag. The timeout and accuracy are analyzed. When adjusting the timeout dynamically according to the traffic arrival intensity and Bloom filter vector length, the mechanism can get minimum error. The experiments are conducted based on the real network trace. The results demonstrate that the proposed method is more accurate than the existing algorithms.

Network measurement; Traffic measurement; Heavy hitters; Dynamic adjust

TP393.06

： A

：1009-5896(2015)04-0887-07

10.11999/JEIT140820

2014-06-23收到，2014-09-15改回

国家自然科学基金(61309019)和国家863计划项目(201101A103, 2011AA010603)资助课题

*通信作者：侯颖 ndschy@139.com