压缩频谱的差分跳频信号在莱斯衰落信道下的性能分析

董彬虹 唐 鹏杜 洋 程郁凡

(电子科技大学通信抗干扰技术国家级重点实验室 成都 611731)

压缩频谱的差分跳频信号在莱斯衰落信道下的性能分析

董彬虹 唐 鹏*杜 洋 程郁凡

(电子科技大学通信抗干扰技术国家级重点实验室 成都 611731)

差分跳频(DFH)信号具有良好的抗多径衰落、抗干扰及高速数据传输能力，在短波和水声军事通信领域得到广泛应用。但是，在有限的传输带宽内差分跳频信号编码增益受限，特别是每跳携带多个比特时，该文提出一种压缩频谱DFH(CS-DFH)方法，可以在相同的比特每跳(BPH)和带宽下提高DFH信号的编码增益。对CS-DFH信号在莱斯(Rice)衰落信道下的误比特率(BER)理论上界进行了推导，并通过仿真验证。结果表明，莱斯信道中，在相同BPH、带宽条件下，与常规DFH相比，CS-DFH是一种可以获得更高BER增益的方法，特别是当莱斯因子K很小的时候。

无线通信；差分跳频；莱斯信道；压缩频谱；编码增益；误比特率

1 引言

1996年，文献[1]首先提出了差分跳频(Differential Frequency Hopping, DFH)技术。该技术把数据信息映射到载波频率跳变路径，并利用频率调制域的编码冗余来纠正错误，从而提高系统抗衰落、抗干扰能力和数据传输速率。在加性高斯白噪声(AWGN)和瑞利(Rayleigh)衰落信道下，DFH表现出良好的性能，与快速跳频、直接序列扩频相比，具有更好的抗多音干扰、低截获与低检测概率性能[2−4]。因此，DFH技术在具有时变特性的短波、水声通信和网络通信领域受到了极大关注[5−8]。

在DFH系统中，当前跳发送的频率取决于当前的数据符号和前一跳发送的频率。如果一个数据符号为Xk且前一跳频率为Fk−1，则下一跳频率定义为

其中，G函数是频率转移函数，决定了DFH系统主要性能。

近年来，文献[9-11]提出信息驱动跳频(Message-Driven Frequency Hopping, MDFH)技术，采用类似于差分跳频的思路，利用FFH系统的部分信息比特流驱动跳频序列，提高了FFH系统的频谱效率。文献[12]提出了Turbo差分跳频(Turbo-DFH)系统，DFH, CS-DFH)方法思——路类似于扩频通信中的OFDM，在有限的带宽内尽量紧凑地利用频谱资源。与现在普遍应用于信号检测领域中的压缩频谱感知技术[14,15]有所不同：压缩频谱感知技术主要利用信号在某一表示域上具有的稀疏性或可压缩性来降低奈奎斯特采样率，以此降低频谱检测中数据量和硬件设备复杂度，最后通过最优化问题重构出原始信号；本文提出压缩频谱技术，主要应用于跳频通信领域，对各频点间隔进行压缩，从而保证在相同带宽下能够得到更大的编码增益。实验证明相比于常规的DFH技术，在相同条件下，虽然压缩频谱引入了频谱泄露，对误比特率(BER)有影响，但是却带来了更高的编码增益，最终获得了BER性能提高。最后本文对其在莱斯衰落信道下的BER性能进行了理论推导和仿真验证。并经仿真验证其BER性能显著优于常规DFH。在更深入的研究后，白玉洁等人提出了非二进制Turbo差分跳频(Nonbinary-Turbo- DFH)系统，进一步提高了性能[13]。

在以上文献中，载波频率是正交的，当传输带宽受限时，为了进一步提高DFH的编码增益，本文提出了一种压缩频谱DFH(Compressed Spectrum

2 系统模型

在常规DFH中，为了保证频谱正交，相邻的频率间隙是Δf=1/Ts，其中，Ts是信号传输间隔。在CS-DFH中，定义Δf=η/Ts,0＜η≤1，其中η定义为频谱压缩因子。那么第k跳的频率可以表示为fk=k×η/Ts, k=0,1,…,Nh−1，其中Nh是跳频集中频率的个数。例如，在相同传输带宽条件下，当Nh=64的常规DFH系统，如果使用η=1/2压缩频谱，对应的CS-DFH中的Nh可增加为128。CS-DFH系统框图，如图1所示。

如果第k跳传输信号是

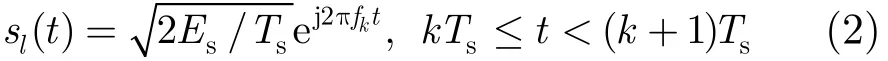
其中Es是符号能量，fk是第k跳的频率。接收信号的等效低通信号应为

图1 CS-DFH系统框图

其中c是莱斯衰落过程，可以表示为

其中m表示直接路径的镜像分量，α表示瑞利衰落分量；ϕ和θ是随机相位，均匀分布在[−π,π]上；n(t)是复高斯白噪声信号，其功率谱密度为N0(W/Hz)。莱斯因子K可以定义为K=m2/，表示视距(Line Of Sight, LOS) 分量和非视距(Non Line Of Sight, NLOS)多径分量的能量比，其中是α2的平均值。当K=0时，信号传输只存在瑞利衰落分量，莱斯衰落信道蜕化为瑞利衰落信道；当K=∞时，信号传输只存在直接路径分量，此时莱斯信道蜕化为高斯信道。不失一般性，本文列举了K=0, 2和 10的性能。

假设第k跳频率为f0，发送信号为s0l(t)，任意可用频点fn处的信号为snl(t)，可得[16]

其中，Δk表示两频率序列号的距离。定义ρΔk为等效低通信号之间的复相关系数，表达式为

|ρΔk|2为信号s0l(t)在fn频点上的泄漏功率与信号功率比值。根据式(6)可知，f0与第1旁瓣上产生的频谱泄露最大相差约13 dB。因此，第1旁瓣对信号的影响很小，在理论推导中只考虑信号在主瓣上对频点的频谱泄漏。

3 CS-DFH理论性能

本文中，对CS-DFH系统在莱斯信道下的比特误码率(BER)的紧密上边界进行了理论推导。在推导中，本文假设η=1/4，对于其他η值也可以用类似的方法推导。

网格图模型可以很方便地分析DFH的G函数特性。对于比特每跳(Bit Per Hop, BPH)为1且 Nh=8的网格图，如图2所示。横轴表示时间间隔，纵轴表示G函数的移位寄存器状态，分支代表当前输出频率。虚线表示输入比特为‘1’，实线表示输入比特为‘0’。

参照文献[16]，图2所示的网格图可以类似转换为图3所示的状态转移图。图3中输入非零符号引入因子Y，输出不为f0引入因子Z。当η=1/4时，考虑信号对主瓣上其它跳频点的频谱泄漏，在输出为f1引入因子H，在输出为f2引入因子I，在输出为f3引入因子J。

图2 状态网格图示例

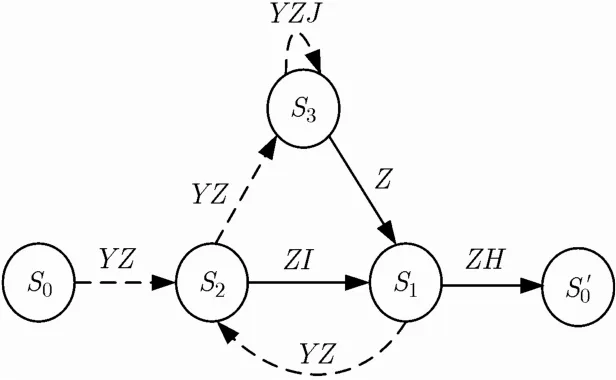
图3 状态转移图示例

根据状态图可以写出状态方程，卷积码的转移函数定义为T(·)=/S0，其中，S0表示输入状态，表示输出状态[16]。由状态方程求转移函数，可得

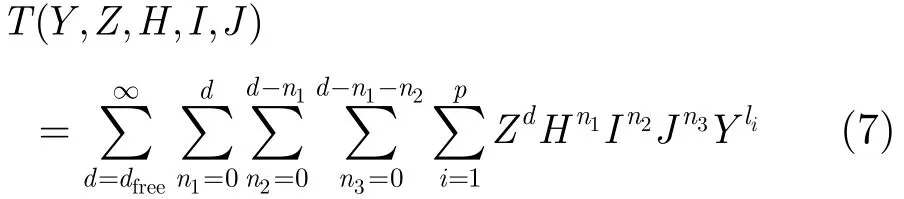
其中dfree是最小自由距离，n1, n2, n3分别表示在d符号不同的成对比较路径中频点f1, f2, f3的数目。为了方便理论推导，本文定义n4=d−n1−n2−n3，表示在有d符号不同的成对比较路径中未受到f0的频谱泄漏影响的频率数目。p表示满足d和n1, n2, n3条件时的路径数目。li表示满足d和n1, n2, n3条件时第i条路径输入非零符号的个数。对Y求导数，并令Y=1，可得

与文献[16]中卷积码BER性能联合界的推导方法相似，可以得到误符号率上边界为

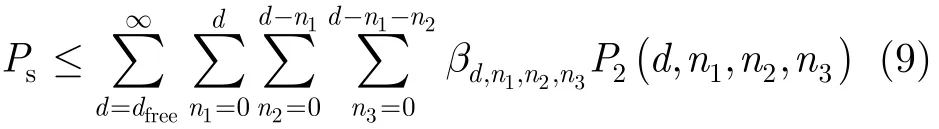
其中，P2(d,n1,n2,n3)表示在d和n1,n2,n3条件下的成对比较路径的差错概率。

根据文献[16]中附录B，条件成对比较路径的判决变量可用复高斯随机变量的一般二次形式的特殊情况表示

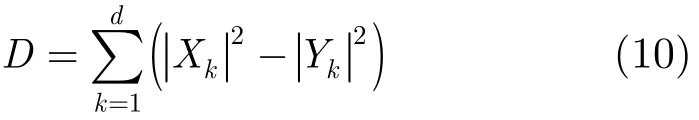
其中，变量{Xk}和{Yk}定义为

其中，s0l(t)是当前发送波形，snl(t)是其他波形。对于所考虑的信道，d对变量{Xk,Yk}是相互统计独立且同分布的高斯随机变量。但是，对于任意k，则Xk和Yk可能是相关的。

差错概率P2(d,n1,n2,n3)是D＜0的概率，即

可以得到系统BER。

4 理论结果和仿真

本文中，CS-DFH系统的信号传输间隔为Ts=200μs且BPH=2, G函数采用移位寄存器结构，如无特殊说明，参数如表1所示。

表1 G函数参数选择

经过计算，当式(9)中d≥1.5dfree, Ps基本趋于稳定。因此，下面的理论分析中均采用d=1.5dfree近似计算Ps。

当η=1/4且K=10时，CS-DFH系统在莱斯衰落信道下的理论和仿真BER性能对比如图4所示。显然理论上界随着信噪比的增加逐渐逼近仿真曲线，这是因为式(9)中不同路径的首次差错事件概率重复累加，导致理论界大于仿真结果。但是，随着的增大，首次差错事件概率重复累加造成的误差迅速减小，理论上界迅速逼近仿真结果。图4的结果证明了理论分析的正确性。

为了说明K与频谱泄漏之间的关系，当η=1和1/2时，均采用相同的编码器结构，其生成多项式为[40,20,10,4,2,1], Nh=64。从图5中可以看出，当BER=1×10−5, K=0, 2和10时，η=1和η=12的BER性能曲线之间差距分别为0.242 dB, 0.424 dB和0.529 dB，也就是说，随着K取值的增加，对频谱泄漏的影响在变大，这说明K因子与频谱泄漏之间有直接关系，但是从变化的大小来看，K因子变化对频谱泄露的影响并不是线性变化的。

图6(a)～图6(c)描述了相同BPH和带宽下的莱斯衰落信道中不同的K因子(K=0, 2和10)和η(η=1,1/2,1/4,1/8和1/16)对BER性能的影响。结果显示，对于不同的K因子，在η选取的范围内CS-DFH系统都存在一个性能最好的压缩因子，即最优压缩因子η；这是因为在带宽一定的条件下，CS-DFH的性能主要由编码增益和频谱泄露决定。随着η的减小，提高了编码增益，但是随着η的进一步减小，频谱泄露带来的性能损失也进一步增加，因此在编码增益和频谱泄漏之间有一个折中。

当相同带宽下，BER为1×10−5时，对比常规DFH，图6(a)～图6(c)中最优压缩因子η和最大增益Gη如表2所示。可以看出，当K变化的时候最优压缩因子η和最大增益Gη也会变化；这是因为在其他频点上的频谱泄漏与K因子是有关的；从图5也可以看到，随着K的增大，频谱泄漏的影响也在增大，所以最优压缩因子η在变大，最大增益Gη在减小。因此本文可以得出当K因子很小的时候，CS-DFH可以获得更高的性能增益。

表2 最优压缩因子η和最大增益Gη(BER = 1×10−5)

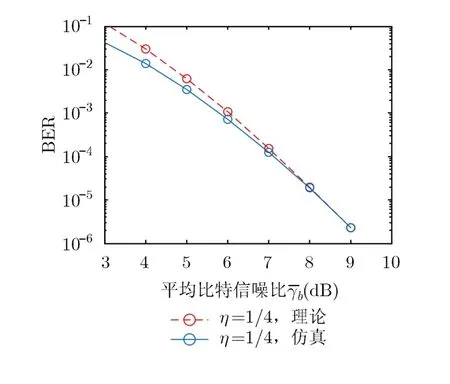
图4 莱斯衰落信道下CS-DFH理论和仿真性能对比(K=10)

图5 相同编码K变化对CS-DFH性能的影响

图6 不同莱斯因子K下，CS-DFH在不同η(η=1, 1/2, 1/4, 1/8和1/16)时的性能对比

5 结束语

为了提高DFH的性能，本文提出了一种压缩频谱的方法。并对CS-DFH 系统在莱斯衰落信道下的性能进行了详细理论推导和仿真验证。结果表明，在带宽和BPH相同的条件下，特别是在莱斯因子K很小的衰落信道中，相比常规DFH，CS-DFH可以获得更高的编码增益。

[1] Herrick D L and Lee P K. CHESS a new reliable high speed HF radio[C]. Proceedings of the IEEE Military Communications Conference'96, McLean, Virginia, USA, 1996: 684-690.

[2] Mills D G, Edelson G S, and Egnor D E. A multiple access differential frequency hopping system[C]. Proceedings of the IEEE Military Communications Conference'03, Boston Massachusetts, USA, 2003: 1184-1189.

[3] Mills D G, Egnor D E, and Edelson G S. A performance comparison of differential frequency hopping and fast frequency hopping[C]. Proceedings of the IEEE Military Communications Conference'04, Monterey, California, USA, 2004: 445-450.

[4] 王胜涛, 黄文晶, 张劲心, 等. 差分跳频信号抗多音干扰性能仿真分析[J]. 无线电工程, 2013, 43(12): 29-31.

Wang Sheng-tao, Huang Wen-jing, Zhang Jin-xin, et al.. Performance simulation analysis on differential frequency hopping signal against multi-tone jamming[J]. Radio Engineering, 2013, 43(12): 29-31.

[5] Cazzanti L, Egnor D, Edelson G S, et al.. Improved multipath robustness of DFH modulation in the underwater acoustic channel[C]. Proceedings of the IEEE OCEANS 2010, Seattle, Washington, USA, 2010: 1-6.

[6] Wang Yong-bin, Liu Hong-bo, Liu Qin-tao, et al.. Project design of a shortwave narrowband difference frequency hopping system[C]. Proceedings of the IEEE 3rd International Conference on Consumer Electronic, Communications and Networks 2013, Xianning, China, 2013: 454-456.

[7] 甘良才, 吴双元. 一种基于差分跳频转移函数的短波跳频码[J]. 电子与信息学报, 2005, 27(2): 218-220.

Gan Liang-cai and Wu Shuang-yuan. A kind of shortwave frequency hopping code based on DFH transform function[J]. Journal of Electronics & Information Technology, 2005, 27(2): 218-220.

[8] 陈卓, 王殊, 王典洪, 等. 基于拉丁方的认知差分跳频网络自适应频率集方法[J]. 武汉大学学报(理学版), 2014, 60(3): 249-254. Cheng Zhuo, Wang Shu, Wang Dian-hong, et al.. A frequency set adaptive optimization algorithm for differential frequency hopping network based on cognitive radio and latin squares[J]. Journal of Wuhan University (Natural Science Edition), 2014, 60(3): 249-254.

[9] Ling Qi and Li Tong-tong. Message-driven frequency hopping: design and analysis[J]. Wireless Communications, 2009, 8(4): 1773-1782.

[10] Zhang Lei, Wang Hua-wei, and Li Tong-tong. Anti-jamming message-driven frequency hopping-part I: system design[J]. Wireless Communications, 2013, 12(1): 70-79.

[11] Zhang Lei and Li Tong-tong. Anti-jamming message-driven frequency hopping-part II: capacity analysis under disguised jamming[J]. Wireless Communications, 2013, 12(1): 80-88.

[12] Pei Xiao-dong, He Zun-wen, and Kuang Jing-ming. Study on turbo-DFH technique[C]. Proceedings of 2005 International Conference on Communications, Circuits and Systems, Hong Kong, China, 2005, 1: 31-34.

[13] 白玉洁, 吕吉贺, 白凤山. 一种Nonbinary-Turbo-DFH方案及译码算法[J]. 通信技术, 2013, 46(9): 12-14.

Bai Yu-jie, LüJi-he, and Bai Feng-shan. A nonbinaryturbo-DFH system and decoding algorithm[J]. Journal of Communications Technology, 2013, 46(9): 12-14.

[14] El-khamy S E, Abdel-Malek M B, and Kamel S H. An improve reconstruction technique for wavelet-based compressive spectrum sensing using genetic algorithm[C]. Proceedings of the 31st National Radio Science Conference (NRSC), Cairo, Egypt, 2014: 99-106.

[15] Stinco P, Greco M, Gini F, et al.. Compressed spectrum sensing in cognitive radar systems[C]. Proceedings of the 2014 IEEE International Conference on Acoustic, Speech and Signal Processing (ICASSP), Florence, Italy, 2014: 81-85.

[16] Proakis J G and Salehi M. Digital Communications[M]. 5th ed, New York: McGraw-Hill, 2008: 45-48, 109-110, 491-516, 1090-1095.

董彬虹： 女，1972年生，教授，研究方向为无线通信系统的抗干扰技术、差分跳频通信系统关键技术.

唐 鹏： 男，1989年生，硕士生，研究方向为无线通信、差分跳频通信系统关键技术.

杜 洋： 男，1988年生，博士生，研究方向为无线通信、差分跳频通信系统关键技术.

程郁凡： 女，1971年生，教授，研究方向为快速跳频通信技术、自适应抗干扰技术、干扰检测与识别技术.

Performance of a Compressed Spectrum Differential Frequency Hopping Signal over Rician Fading Channel

Dong Bin-hong Tang Peng Du Yang Cheng Yu-fan
(National Key Laboratory of Communication, University of Electronic Science and Technology of China, Chengdu 611731, China)

Differential Frequency Hopping (DFH) signal can be used in the High Frequency (HF) and underwater acoustic communications because it has good resistance to multipath fading and jamming, at the same time with a high-speed data transmission capacity. However, taking into account the coding gain is limited within a finite transmission bandwidth, especially multiple Bit Per Hop (BPH), a Compressed Spectrum DFH (CS-DFH) method is proposed to increase the coding gain of DFH signal for the same BPH and bandwidth. This paper develops an upper bound on the Bit Error Rate (BER) of CS-DFH signal in Rician channel, and its tightness is proved by simulations. For the same BPH and bandwidth, the results indicate that the CS-DFH is an efficient mean for obtaining higher coding gain than the existing DFH over the Rician channel, especially when the Rician factor K is small.

Wireless communication; Differential Frequency Hopping (DFH); Rice channel; Compression Spectrum (CS); Coding gain; Bit Error Rate (BER)

TN914.41

： A

：1009-5896(2015)04-0836-05

10.11999/JEIT140908

2014-07-11收到，2014-10-27改回

国家自然科学基金(61201126)，新世纪优秀人才支持计划(NCET-11-0058)和四川省青年科技基金(2012JQ0020)资助课题

*通信作者：唐鹏 454847157@qq.com