采用基于密度加权和偏好信息的K均值聚类的胸阻抗信号自动检测算法

李勇明陈勃翰王 品

①(重庆大学通信工程学院 重庆 400044)

②(第三军医大学生物医学工程与医学影像学院 重庆 400038)

采用基于密度加权和偏好信息的K均值聚类的胸阻抗信号自动检测算法

李勇明*①②陈勃翰①王 品①

①(重庆大学通信工程学院 重庆 400044)

②(第三军医大学生物医学工程与医学影像学院 重庆 400038)

为了自动识别胸阻抗(TransThoracic Impedance, TTI)信号中的按压和通气波形，完成相关重要参数的计算，从而实现对心肺复苏质量的监测评估，该文提出一种基于密度加权与偏好信息的胸阻抗信号自动检测算法。该方法针对实验采集的猪的电诱导心脏骤停模型TTI信号，通过预处理和多分辨率窗口搜索法完成潜在按压和通气波形的标记；接着，提取每个标记波形的宽度、幅值以及相邻波形特征差作为特征，并按标记波形宽度对信号进行分段；之后，再对信号进行小波分解，提取其小波系数每段的能量与原始波形幅值之比作为特征；最后采用基于密度加权与偏好信息的K均值聚类分析法对标记的波形进行分类识别。实验结果表明，该算法对TTI信号中按压波形和波形分析识别的正确率和敏感度均较高，鲁棒性好，且运行时间(0.43 s±0.07 s)满足实时性要求。

自动识别；胸阻抗；K均值；密度加权；偏好信息

1 引言

胸外按压(Chest Compression, CC)是心肺复苏(CardioPulmonary Resuscitation, CPR)中试图恢复人体自主循环的重要技术，其在基础生命支持的地位越来越受到重视[1,2]。胸外按压频率，按压通气循环周期，按压通气参数等CPR核心技术是保证CPR质量的关键问题[3,4]。通过对胸外按压的检测分析，实时反馈给救援者为心肺复苏过程提供参考，以此避免不必要的按压中断，并让CPR过程中的ECG检测无瑕疵间隔(例如进行通气的时候)以正确的评估按压节奏，使救援操作更为标准[5,6]。

胸阻抗(TransThoracic Impendance, TTI)信号值主要是指在心肺复苏过程中人体阻抗的变化，其主要包含了操作者实施胸外按压造成人体胸腔形变而产生的阻抗信号以及由心脏和血管内血流等变化引起的阻抗信号变化两方面信息[7]。现已有研究表明，在心肺复苏过程中，胸外按压的快慢、深度均能反映在TTI信号波形中，并且可准确地估算出瞬时的按压频率[8−10]。通过对TTI信号的检测分析，指导胸外按压具有可实施性和积极的参考意义，可增加心肺复苏操作的成功率[11−13]。目前关于波形分析的公开研究较少，其中，文献[14]用自适应阈值法进行按压波形分析，普适性较差，难以适用于复杂的波形；文献[15]采用神经网络进行按压和通气波形的模式识别，时间代价较大，无法达到实时要求，且对特异信号的识别能力较差。目前，通过对TTI信号进行实时检测反应心肺复苏质量的多个参数的研究尚未见公开报道。

因此，本文提出了一种采用基于密度加权和偏好信息的K均值聚类的胸阻抗信号自动检测算法，该算法在对TTI信号进行预处理去噪、多分辨率窗口搜索并完成潜在按压和通气波形的标记后；提取每个标记波形的宽度、幅值以及相邻波形特征差作为特征，并按标记波形宽度对信号进行分段；再对TTI信号进行小波分解，提取其每段小波系数的能量，并将其与TTI信号幅值的比值也作为特征，最后得到代表信号波形特征的4维特征向量；采用基于密度加权与偏好信息的K均值聚类分析法对标记的波形进行分类识别，并根据分类识别结果计算信号所反映的按压频率、按压通气比和按压时间比等参数，最后依此结合2010年心肺复苏指南中的指标智能地评估该次心肺复苏的质量。

2 实验数据

2.1 数据的采集

本实验所使用的是一个基于家猪的电诱导心脏骤停模型的子数据库，涉及16头公猪。实验数据由重庆市第三军医大学大坪医院外科研究所提供。实验所选用的家猪体重均在18～22 kg，并在各项生理参数均趋于稳定时展开实验。实验通过Windaq数据采集系统(DATAQ InstrumentsInc, Akron, OH, USA)对TTI信号进行连续的测量，采样频率为300 Hz。实验采集每次CPR过程前2 min的数据，使每组TTI信号均包括一个120 s的连续信号波形。

2.2 信号数据

TTI信号中连续的波峰-波谷波形即为一次胸外按压[16]。在每次按压过程中，TTI信号的振幅变化为通过数据采集系统测量的阻抗波形其波峰和波谷之间的差异。图1所示为本次实验所采集到的部分TTI信号：图1(a)信号为较标准信号波形，可以看出信号波形的按压部分和通气部分对比分明，容易识别；图1(b)信号中，由于按压不规范，信号中出现了与通气相近的波形；图1(c)信号中，由于高频噪声和基线漂移的干扰，导致信号部分区域难以识别。

3 胸阻抗信号自动检测算法

3.1 基于多分辨率窗口搜索法的波形标记

TTI信号中的噪声主要由高频噪声和基线漂移组成。其信号中的高频噪声都是尖锐锋形，且幅值较小。通过小波去噪处理后，再通过移动平滑处理器，信号中的噪声和干扰被消除，并平滑了信号波形。TTI波形可看作是采样点的函数，我们把这个函数看作f(·)。TTI波形的波峰、波谷搜索可以看作为极值搜索。然而，实际上波形受到了多重干扰导致了伪波和复合波形的生成，所以经典的寻优方法(如局部优化法)是无效的。

多分辨率分析是一种有效的信号处理方法，可采用不同的分辨率处理同一信号。通过采用这种方法，可以寻找到不同分辨率下的局部最优值，然后通过梳理他们得到更加精确的最优值。设有n个分辨率，在不同分辨率下，搜索窗口的宽度均不同。本文中r=3，即有3个分辨率，搜索窗口宽度分别设为20, 40, 60。如果判定pi是否为极值点，那么首先在第1个分辨率下通过式(1)和式(2)进行搜索。

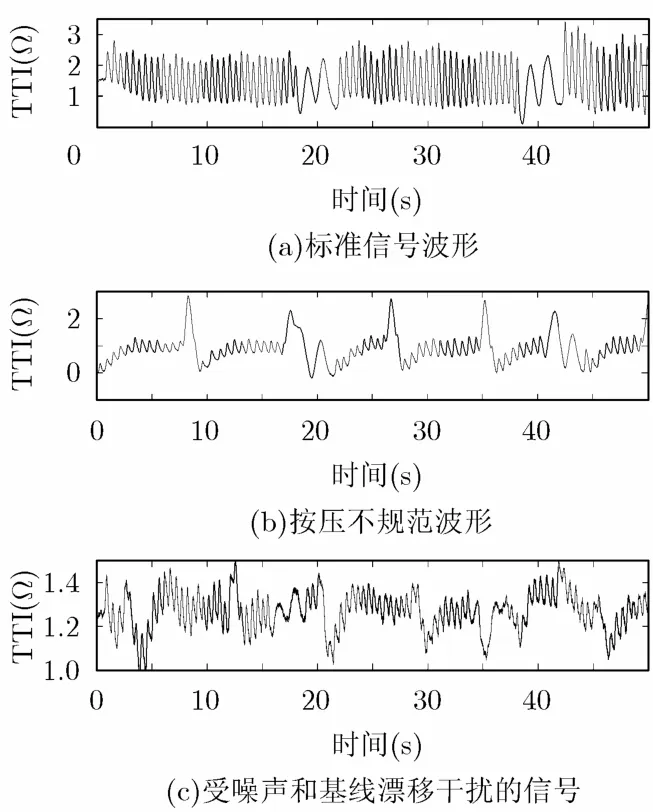
图1 原始信号

若式(1)或式(2)成立，则判定权值k=k+1(每次搜索k的初始值均为为0)。然后依次在其他分辨率下进行搜索。如果k＞0.5r，那么点pi即可被判定为波峰或波谷点。

尽管多分辨率窗口搜索法能够正确识别所有的波峰和波谷，但仍可能存在少量伪局部极值点。而这些伪局部极值点实际为伪波和复合波形所造成的。因此，需要将其消除。通过观察以及先验知识，算法提取信号波形振幅(波峰与紧跟波谷之差)和时间跨度(波峰前后相邻波谷距离)为特征。在(每一次)识别潜在波峰或者波谷后，相邻波峰或波峰之间的幅度距离和时间距离的均值都会被计算一次。设每次计算的均值分别为Mad和Mtd，每一相邻波峰或波谷之间的幅度距离(Da)和时间距离(Dt)都会将与均值Mad和Mtd比较。假设第i个相邻波峰或波谷的幅度距离和时间距离分别为Dai和Dti。如果Dai＜mMad或Dti＜mMtd(其中m为阈值系数，本文中取m=0.1)，那么该波峰或波谷则判定为错误波峰和波谷。

3.2 特征提取

3.2.1 TTI信号波形特征的提取 在TTI信号波形的波峰和波谷被正确标记之后，即可得到每个波形的宽度L和幅值H，并依据每个波形的宽度对信号进行分段。由于胸外按压的规律性，即国际规定的标准按压通气比为30:2。则可断定大部分的通气为连续的两个波形，且区别于按压波形(由图1(a)可以看出)。因此，可提取每个波形与相邻波形的特征差作为其特征，则第n个波形的相邻特征差为

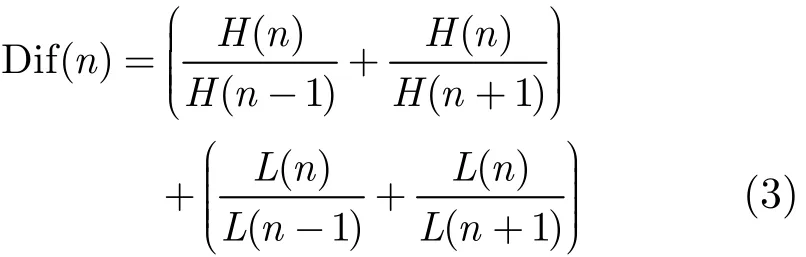
3.2.2 基于小波分解的特征提取 小波分析方法是一种强大的时-频域局部化分析方法。通过对小波函数的平移和缩放，可以将信号表示为若干描述不同子频带的时频域分量之和，达到细微观察原始信号特定频率特性的目的。由图1中可以看出，按压波形部分波形与通气部分波形呈现较明显差异，其宽度主要在0.5 s左右。因此，在按压和通气波形识别中，可以通过小波分解突出按压波形部分特征，并弱化通气波形特征，而达到区分两种波形的目的，可参见图2中不同尺度下的分解效果。

从离散小波分解分频的原理出发，利用离散小波对TTI信号进行分解，每一层子频带是由高频向低频对信号频率空间逐次进行二分的结果。如果原始信号频率空间V0=[0,fs],则第1层小波系数频率空间W1=[2−1fs,fs]，第2层小波系数频率空间W2=[2−2fs,2−1fs]，以此类推，第N层小波系数频率空间为WN=[2−Nfs,2−N+1fs]逐级向低频过度，其中fs为胸阻抗信号的采样频率。

在按压和通气波形中，相较下通气波形频率更小，其对应频率为

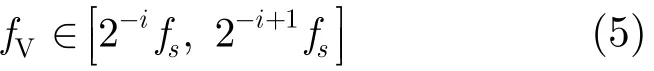
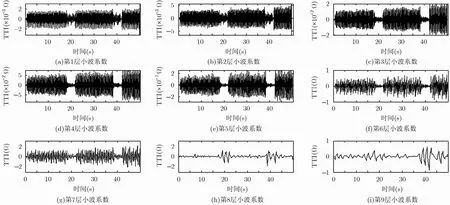
图2 1～9层细节小波系数图

其中B为通气波形宽度。因此总是存在层数i，使得也就是说，通气波形特征可以在第i层小波分解中得到体现。

由实验数据可得，通气波形的宽度约在[400,600]。因此根据式(4)可计算得到通气波形宽度所对应的频率为fV=fs/B=300/600=0.5。据式

其中H(n)为第n个波形的幅值，p(n)为第n个波形对应该段小波系数的能量。图1(a)标准信号的Dw特征曲线如图3所示。(5)计算可知，此波形特征落在第9层细节小波的子频带范围内，因此，可以确定最优的分解层数为9层。利用db2小波对图1(a)原始信号进行9层小波分解，其分解结果中1～9层细节小波系数如图2所示。

分析此结果可知，对原始信号进行小波分解后，在第5层细节小波函数可观测到按压波形部分和通气波形部分对应的小波系数波形差别十分明显。同时，在TTI信号波形中幅值较小的按压波形所对应的小波系数幅值也较小，为排除此种干扰，因此选用原始波形幅值与其所对应段的第5层小波系数能量之比作为特征

图3 Dw的特征曲线图

如3图所示，通气波形的Dw特征值远大于按压波形的Dw值，因此其可作为按压、通气的分类依据。

3.2.3 归一化 在分别进行上述两种特征提取算法后，即可得到由TTI原始信号中按压、通气波形的宽度L，幅值H、相邻波形特征差Dif以及幅值与小波系数能量之比Dw组成的4维波形特征向量。而每个特征之间的权重是相同的，因此采用线性归一化

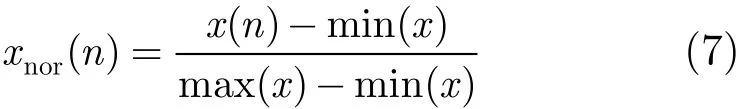
其中xnor(n)为归一化结果，x(n)为特征。根据式(7)将特征归一化至[0,1]区间。

3.3 基于密度加权与偏好信息的K均值分类识别

K均值聚类算法被广泛用于模式识别，其实现步骤较简单，不需长时间的训练过程，非常适用于动态实时检测。当聚类是密集的，该算法可通过调节k值取得较好的聚类效果，具有较好的灵活性。根据前面的特征提取数据分析可知其聚类相对密集，并且算法对时间代价要求较高，因此选用K均值聚类算法进行波形的分类识别。

在传统K均值聚类算法中，对样本的聚类仅仅依据其与聚类中心的距离来判定。但在实际中，由于较少通气波形与按压波形可能相似，使其偏离通气波形特征数据聚类中心而靠近按压波形特征数据聚类中心。而按压波形特征数据数量较多，构成了数据密集区域；通气波形特征数据较小，构成的区域非密集。因此，若在对数据进行聚类的过程中根据每个数据所在区域的密度调整权重，使偏离的数据点更好地靠近所属聚类中心点，分类的准确性将会得到改善。

对于一个有N个样本的数据集U={xi,i=1, 2,…, N}，定义点xi处的密度函数为

其中∂表示邻域的有效半径，这里我们取N个样本的均方根距离，即

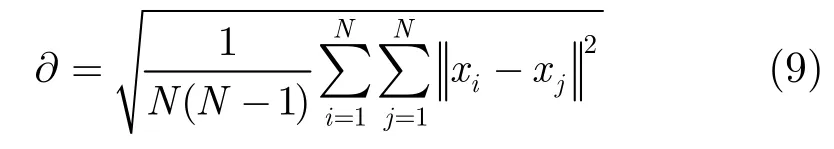
由式(8)和式(9)可见，xi周围聚集的样本越多，xi的密度值dens(xi)越大。如图4所示为加权前后的K均值分类结果对比图(图中只显示了特征向量的Dif, L和Dw3个特征，其中○表示为通气波形特征点，*表示为按压波形特征点)。

由于两类数据所隶属的聚类中心是不同的，按压波形特征数据值均较小，通气波形特征数据值均较大，所以我们将密度值较小的赋予较大的权值，密度值较大的赋予较小的权值。xi的权重wi定义为

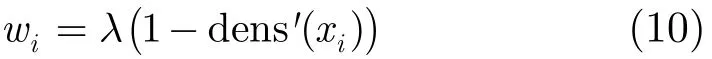
式中dens'(xi)为dens(xi)的归一化结果，λ参考∂的值(均在[0.05，0.1]范围内)取λ=0.1。所以，密度加权后的特征数据为

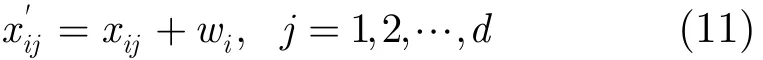
式中，xij为特征数据，x'ij为新的特征数据，d为特征向量维数。

通过密度加权可修正偏离通气波形特征数据聚类中心而靠近按压波形特征数据聚类中心的特征数据。而信号中同样可能存在与通气波形相似的按压波形需要修正。根据先验知识，可知标准的按压通气比为30:2，通气波形大部分为连续两个波形，但也可能存在单个波形。因此，可加入偏好信息对孤立伪按压波形进行修正。

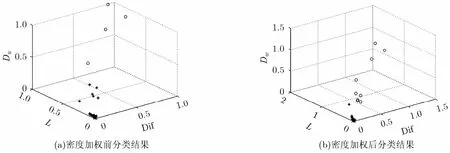
图4 密度加权前后的分类结果对比图

在进行基于密度加权的K均值聚类分析可得到初步的按压波形聚类结果Ccc和通气波形聚类结果CV。那么对CV中的孤立波形特征数据进行加权的算法如下：

(1)对CV中的孤立波形特征数据进行加权，加权公式为

(2)进行K均值聚类；

(3)判定按压通气比，如果大于14，则算法结束，否则转到第(1)步。

由图5可以看出，矩形框中的孤立伪按压波形并未被识别出，而仅识别出了真正的按压波形，达到了良好的去伪效果。

3.4 胸外按压质量评估

在完成按压和通气波形的分类识别后，可计算出按压次数为C，通气次数为V。每个被正确分类识别的按压和通气波形的波峰序列号(采样点)分别为CInc和VInv, nc, nv分别为按压和通气序号。那么可以得到实时按压频率fc：

按压通气比P：

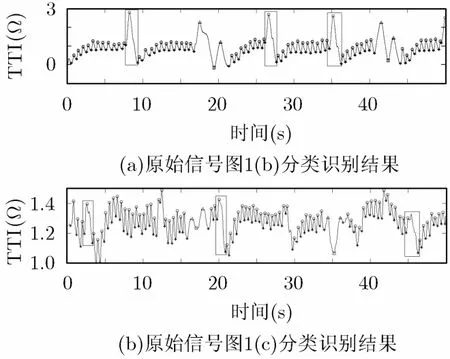
图5 原始信号图1(b)图1(c)分类识别结果

按压时间比cP(按压时间在整个CPR过程时间中的比例)：

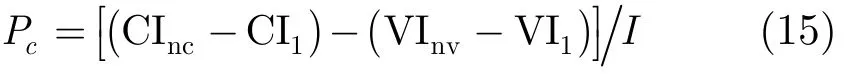
式中I为信号当前采样点数。

4 实验结果与分析

将本文方法与Digna的阈值法[12]和Martin的神经网络法[13]一起对已去噪除伪的TTI信号进行分类识别的结果对比。结果主要从阳性检出率(Positive Predictive Value, PPV)以及敏感度两个指标来显示。结果如表1所示。

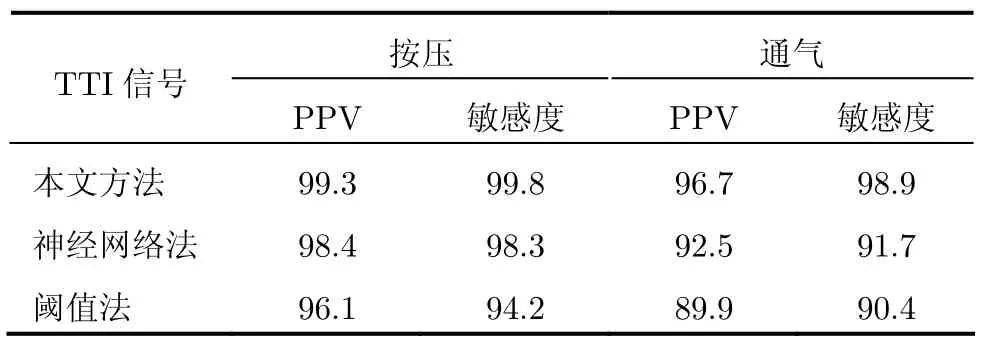
表1 分类识别效果(%)

由表1可以发现，其他方法的检测效果总体较差，如采用神经网络对训练样本要求较高，并由于部分按压波形和通气波形的波形特征相似，因此抗伪波能力较差；阈值法由于其参数都相对固定，而不同的TTI信号中按压波形和通气波形的特征差异均不尽相同，相同参数无法对所有的信号进行准确的分类识别，并且抗伪波能力也较差，因此识别结果不够理想。胸阻抗信号自动检测本质上可以看成是模式分类问题。如前面所述，该信号具有细小的波动、漂移等特点，因此传统的极值法、局部优化法等会得到多个伪波峰波谷，效果差强人意。针对多个分辨率来进行极值判断将能够明显减少伪波峰波谷的出现。在一般情况下，通气和按压的区别是不标准的，因此为了能够更好地区别它们，需要提取优秀的特征。通过小波的多级分解发现，小波特征能将时域下两类的区别放大，因此便于提高分类准确率。本文的自动检测对时间代价要求较高，当样本密集时，神经网络等方法由于需要训练收敛获取适宜的权值，因此变得并不适宜。相比来说，K均值聚类算法通过调节值，可以很好地兼顾分类准确率和时间代价。由于我们还有临床医生的先验知识，K值选择较为容易，因此K均值聚类算法在本文中较佳。检测最终效果也显示其具有良好的鲁棒性和较高的阳性检出率(PPV)，其识别按压波形和通气波形的PPV为99.3%和96.7%，敏感度也可分别达到99.8%和98.9%。此外，每组数据(共36000个采样点)均可在0.43±0.07 s之内完成处理，可以达到对TTI信号进行实时监测。

5 结束语

本文将胸阻抗信号波形的形态特征与小波特征相结合，提出了采用基于密度加权和偏好信息的K均值聚类的胸阻抗信号自动检测算法。实验结果表明：本文算法能有效地排除大部分畸变和噪声的干扰，正确地识别按压和通气波形，并达到实时处理的要求，从而正确地计算出分析TTI信号所需的按压频率、按压通气比和按压时间比等参数各项。以此向心肺复苏操作人员实时地反馈按压通气信息，调整其心肺复苏操作，达到为CPR过程提供指导，提高心肺复苏成功率的目的。

[1] Tomoya Hirose, Taku Iwami, Hiroshi Ogura, et al.. Effectiveness of a simplified cardiopulmonary resuscitation training program for the non-medical staff of a university hospital[J]. Resuscitation and Emergency Medicine, 2014, 22(31): 1-7.

[2] Al-Alwan A, Ehlenbach W J, Menon P R, et al.. Cardiopulmonary resuscitation among mechanically ventilated patients[J]. Intensive Care Medicine, 2014, 40(4): 556-563.

[3] Stiell I G, Brown S P, Christenson J, et al.. What is the role of chest compression depth during out-of-hospital cardiac arrest resuscitation?[J]. Critical Care Medicine , 2012, 40(4): 1-7.

[4] Bobrow B J, Spaite D W, Berg R A, et al.. Chest compression-only CPR by lay rescuers and survival from out-of-hospital cardiac arrest[J]. JAMA, 2010, 304(13): 1447-1454.

[5] de Gauna S R , Gonzalez-Otero D, M.Ruiz J M, et al.. Is rhythm analysis during chest compression pauses for ventilation feasible?[J]. Resuscitation, 2012, 83(S1): e8.

[6] Kim Seung-hwan, You Je-sung, Lee Hye-sun, et al.. Quality of chest compressions performed by inexperienced rescuers in simulated cardiac arrest associated with pregnancy[J]. Resuscitation, 2013, 84(1): 98-102.

[7] Aramendi E, Ayala U, Irusta U, et al.. Suppression of the cardiopulmonary resuscitation artefacts using the instantaneous chest compression rate extracted from the thoracic impedance[J]. Resuscitation, 2012, 83(6): 692-698.

[8] Ristagno G. Transthoracic impedance waveform during cardiopulmonary resuscitation: One size does not fit all![J]. Resuscitation, 2014, 85(5): 579-580.

[9] Di Maio R, Howe A, McCanny P, et al.. Is the impedance cardiogram a potential indicator of effective external cardiac massage in a human model? a study to establish if there is a linear correlation between the impedance cardiogram and depth in a cardiac arrest setting[J]. Resuscitation, 2012, 83(S1): e62.

[10] Alonso E, González-Otero D, Aramendi E, et al.. Can thoracic impedance monitor the depth of chest compressions during out-of-hospital cardiopulmonary resuscitation?[J]. Resuscitation, 2014, 85(5): 637-643.

[11] Losert Heidrun, Risdal Martin, Sterz Fritz, et al.. Thoracic impedance changes measured via defibrillator pads can monitor ventilation in critically ill patients and during cardiopulmonary resuscitation[J]. Critical Care Medicine, 2006, 34(9): 2399-2405.

[12] Hehua Zhang, Zhengfei Yang, Zitong Huang, et al..

Transthoracic impedance for the monitoring of quality of manual chest compression during cardiopulmonary resuscitation[J]. Resuscitation, 2012, 83(10): 1281-1286.

[13] Ayala Unai, Eftestøl Trygve, Alonso Erik, et al.. Automatic detection of chest compressions for the assessment of CPR-quality parameters[J]. Resuscitation, 2014, 85(7): 957-963.

[14] González-Otero D, de Gauna S R, Ruiz J, et al.. Automatic detection of chest compression pauses using the transthoracic impedance signal[C]. 39th Conference on Computing in Cardiology, AGH Univ Sci & Technol, Krakow, POLAND, 2012, 39: 21-24.

[15] Martin Risdal, Sven Ole Aase, Mette Stavland, et al.. Impedance-based ventilation detection during cardiopulmonary resuscitation[J]. IEEE Transactions on Biomedical Engineering, 2007, 54(12): 2237-2245.

[16] Jaime R, Ayala U, De Gauna S R, et al.. Feasibility of automated rhythm assessment in chest compression pauses during cardiopulmonary resuscitation[J]. Resuscitation, 2013, 84(9): 1223-1228.

李勇明： 男，1976年生，博士，副教授，主要从事模式识别、医学信号和图像的处理、智能优化算法方面的研究.

陈勃翰： 男，1990年生，硕士，主要从事模式识别、医学信号的处理方面的研究.

王 品： 女，1979年生，博士，副教授，主要从事医学信号处理、图像处理、智能优化算法方面的研究.

Automatic Detection Algorithm for Transthoracic Impedance Signal Using K-means Clustering Based on Density Weighting and Preference Information

Li Yong-ming①②Chen Bo-han①Wang Pin①

①(College of Communication Engineering, Chongqing University, Chongqing 400044, China)

②(College of Biomedical Engineering and Medical Imaging, The Third Military Medical University, Chongqing 400038, China)

In order to recognize automatically the compression and ventilation waveforms of the TransThoracic Impedance (TTI) signal, and obtain the important parameters, for evaluating the CardioPulmonary Resuscitation (CPR) quality, this paper proposes an automatic detection algorithm for TTI signal based on density weighting and preference information. The TTI signals that come from the pig model based on electrically induced cardiac arrest are preprocessed, and the potential compression and ventilation waveforms are marked by using the searching algorithm of multiresolution window after the pretreatment. After that, the width, amplitude and the difference between the adjacent waveforms of the marked waveforms are selected as the features and the signal is divided into several sections according to the width of marked waveforms. Then the original signal is decomposed by wavelet transform. The ratio of the power of each section to the amplitude of the original one is taken as one feature. Finally, k-means clustering algorithm based on density weighting and preference information is used to recognize and classify the compression and ventilation of the marked waveforms. The experimental results show the accuracy and sensitivity of the recognition are high, the robustness is good and the running time (0.43±0.07 s) can meet the requirement of clinical application.

Automatic detection; TransThoracicImpedance (TTI); K-means algorithm; Density weighted; Preference information

TP391.4; R318.04

： A

：1009-5896(2015)04-0824-06

10.11999/JEIT140903

2014-07-09收到，2014-10-13改回

国家自然科学基金(61108086)，重庆市自然科学基金(CSTC2011BB5066, CSTC2012jjA0612)，重庆市科技攻关计划项目(CSTC2012gg-yyjs0572)，中央高校基金(CDJZR10160003, CDJZR13160008)，军队博士后基金和重庆市博士后基金资助课题

*通信作者：李勇明 yongmingli@cqu.edu.cn