集中式多输入多输出雷达多功能波形优化设计

陈志坤 李风从 乔晓林赵宜楠

(哈尔滨工业大学电子与信息工程学院 哈尔滨 150001)

集中式多输入多输出雷达多功能波形优化设计

陈志坤 李风从 乔晓林*赵宜楠

(哈尔滨工业大学电子与信息工程学院 哈尔滨 150001)

针对集中式多输入多输出(MIMO)雷达波形设计中多个设计目标同时优化的问题，基于交替投影的思想，该文提出一种以任意维迭代谱逼近算法(ADISAA)为基础的波形设计框架，通过可调的权重来协调发射方向图匹配、良好的相关特性和频谱凹口等多种功能的波形设计目标，最终实现恒模波形设计。仿真结果表明，相对于已有的算法，在发射方向图匹配的基础上，该算法改善了发射波形在指定区间的相关特性，同时通过频谱凹口的设计避开了受到色噪声和有源干扰污染的频段，算法的计算复杂度更低。

多输入多输出雷达；波形设计；发射方向图匹配；相关特性

1 引言

多输入多输出(MIMO)雷达的波形设计是MIMO雷达研究领域一个热门方向[1]。与相控阵雷达相比，集中式MIMO雷达可通过改变阵元发射信号之间的相关性来合成空间方向图[2,3]。在搜索目标时，为了尽量获取由虚拟孔径所带来角度分辨率的改善，通过发射正交波形合成全向方向图；当检测到目标时，为了提高参数估计的精度，通过设计发射信号的相关矩阵来将电磁能量尽量辐射到感兴趣的空间范围上，由此达到合理利用有限发射功率满足不同任务需求的目的，提高了积累增益[4,5]。此外，设计具有指定区间良好相关特性的波形可以有效地提高雷达距离分辨率的性能[6]。

2004年，文献[7]推导了MIMO雷达发射方向图的计算公式，采用梯度搜索方法求解了发射信号的相关矩阵，初步提出了通过设计相关矩阵合成MIMO雷达空间方向图的思想。2007年文献[8]修改了方向图的目标函数，用半正定规划方法进行求解，取得了很好的匹配效果。为了最大化利用发射机功率和避免放大器非线性特性导致的波形畸变，MIMO雷达的波形设计需要满足恒模约束。文献[6]在恒模约束条件下对指定区间波形的相关特性进行设计，取得了良好的结果。2012年，文献[9]在之前的基础上，将发射方向图匹配与指定区间良好的相关特性进行结合设计，得到了具有期望方向图和指定区间良好相关特性的恒模波形。然而这两种约束条件联合设计的结果导致了过程变量的矩阵维数过大从而影响波形设计的计算复杂度，而且不具有灵活的调整能力，当设计目标改变时需对整个优化算法进行重新设计，因此该方法不能适应于具有多个功能设计目标的波形设计。

本文提出了一种以任意维迭代谱逼近算法为基础的波形设计框架，能够灵活调整波形设计所需的设计目标，以此实现MIMO雷达波形设计中多种设计目标的同时优化。本文选择了方向图匹配，指定区间良好的相关特性，频谱凹口3种设计目标进行设计，在方向图匹配的基础上，有效地提高了指定区间内的相关特性，频谱凹口的设计可以避开了由有源干扰造成“污染”的频段，最终实现了恒模波形设计，从而提高了MIMO雷达的性能，并有效地降低波形设计的计算复杂度。

2 问题建模

为了最大化利用发射机功率，本文采用的波形模板为恒定幅度的相位调制信号[6]。考虑M个发射阵元， x(n)代表时刻n时雷达所发射的M个信号，定义为

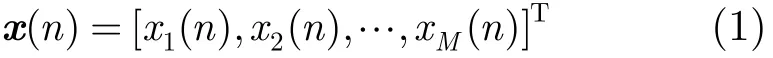
考虑互耦的影响及栅瓣的产生，一般取阵元间距为半个波长，设a(θ)为阵列的导向矢量，则a(θ)为

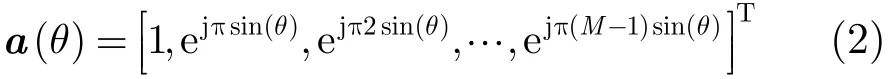
本文综合考虑发射方向图匹配、指定区间良好的自相关特性、频谱凹口等3种功能的设计目标进行结合设计。

2.1 发射方向图匹配

按照环境参数变化灵活设计发射方向图可提高MIMO雷达的整体性能[10]。与相控阵雷达通过权系数来实现天线波束的改变相比，集中式MIMO雷达可通过发射信号协方差矩阵的设计得到期望方向图，因此方向图设计更加灵活。集中式MIMO雷达的方向图可表示为

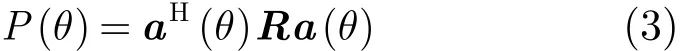
R为x(n)的协方差矩阵，R=E{x(n)xH(n)}。两个不同方向θ1与θ2的互相关则表示为

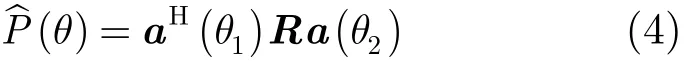
发射方向图匹配拟合的一般流程：设期望方向图为φ(θ)，在最小二乘准则下设计R使得P(θ)逼近φ(θ)，同时使感兴趣的目标方向之间的空域互相关(θ)最小。文献[7]根据方向图与协方差矩阵之间的函数关系建立目标函数，将其转化为一个半正定二次规划(Semidefinite Quadratic Programming, SQP)的问题，通过凸优化理论对其进行优化求解，得到与期望方向图所对应的协方差矩阵R。本文使用建模语言Cvxpy求解这一SQP问题，得到协方差矩阵R，并对应波形矩阵的目标函数进行求解[9]，可得

式中，R1/2为R的Hermitian平方根，且R≥0为半正定矩阵，为矩阵的Frobenius范数。

2.2 指定区间良好的相关特性

文献[11]已经证明，在指定区间具有极低距离旁瓣的波形可以有效减弱距离旁瓣遮蔽。由文献[6]可知，关于指定区间相关特性的设计主要有两种算法：多序列循环新算法(Multi-sequence Cyclic Algorithm-new, Multi-CA)和多序列加权循环新算法(Multi-Sequence Weighted Cyclic Algorithm-New, Multi-WeCAN)。相对于Multi-CA算法，Multi-WeCAN算法虽然实现较为复杂，但能取得更低旁瓣深度，且矩阵的维数较小，有利于减少过程的计算量。设指定区间参数为，令Γ= Toep[γ0,γ1,…,γN−1],Toep为Toeplitz矩阵。另设y(n)=[x1(n), x2(n),…,xM(n)]Τ, ZT(ω)=[y(1)e−jω, y(2)e−jω2,…,y(N )e−jωN]M×N,Zp=Z(ωp),C为Γ的平方根，, p=1, 2,…,2N。由文献[6]可得Multi-WeCAN算法的目标函数为

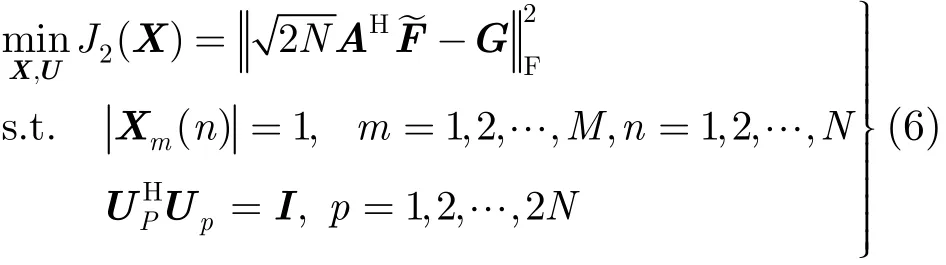
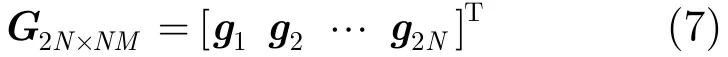
2.3 频谱凹口

在波形设计阶段，需考虑电磁环境中有源干扰和色噪声的影响导致某些频段受到严重干扰，不能作为发射波形的频段，因此波形设计需考虑避开受到“污染”的频段[12]。设定“污染”的频段为sΩ=为k个阻带频段；N为阻带s的个数。设F~N是~ ×N维的单位离散傅里叶变换矩阵(为频率采样点)，F~N中与sΩ对应的频段矩阵为P，对sΩ频段内功率谱的抑制问题可表示为

3 多功能波形优化设计

实际的波形设计常需要考虑多个功能的设计目标，因此需要寻求一种能够针对多个设计目标同时进行优化的算法框架。文献[9]综合考虑方向图匹配和零相关区旁瓣抑制，将方向图匹配与循环算法(Cyclic Algorithm, CA)进行结合设计，得到具有期望方向图和良好相关特性的波形。在该文中，相关特性的约束是在方向图匹配的基础上乘积式实现的，虽然能取得方向图匹配最优的拟合效果，但制约了指定区间的相关特性，且很难与其他的设计目标兼容；另外，由于MIMO雷达本身多通道的特点使得波形设计过程变量矩阵的维数都很大，而采用乘积的方式对矩阵进行扩展，导致了矩阵维数变得更大，从而影响了波形设计的计算复杂度。

文献[13]基于交替投影和相位提取的思想提出了一种多维迭代谱逼近算法，通过迭代的方式，利用了相关和谱之间的关系使得设计的波形逼近理想的波形谱，从而达到波形优化的目的。该算法只对两种设计目标进行优化设计，且不具有灵活的调整能力。本文将从多个设计目标的情况下进行恒模波形设计出发，对该算法在多设计目标的情况下进行扩展和推导，由此实现多设计目标同时优化的问题，并定义：

(1)波形的距离，本文采用了Frobinus范数定义波形距离。

(2)设计目标波形的各种集合，波形集合是用波形矩阵来表示，分别定义集值函数Sp, Scon为第p个设计目标和恒模约束所对应的集合。

(3)每个设计目标集合对应投影算子，但并不是每种设计目标都可用投影算子来优化，需进行转换或推导，这也是本文的难点之一。投影算子表示为

式中proj为投影算子。

3.1 算法框架

基于以上，本文提出了一种任意维迭代谱逼近算法(Arbitrary-Dimensional Iterative Spectral Approximation Algorithm, ADISAA)，假设K为算法的叠加次数，令k=1,2,…,K，当k=1时，X(0)=IM×N，对算法的第k次叠加，求解问题为式中λp为第p个设计目标对应的权重，Pc为设计目标的个数。根据式(10)可得，一种任意维迭代谱逼近算法的波形设计框架如图1所示。

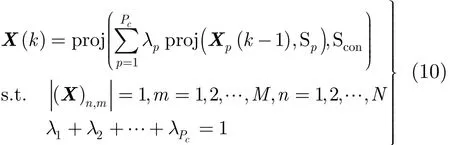
由图1可知，本文所提出波形设计框架是以加权求和及迭代的方式来实现的，设计框架的两种好处为：

(1)可根据任务的需求更换设计目标而不影响整个波形设计的算法框架，如可选择正交波形的设计替换方向图匹配。

(2)权重λp(p=1,2,…,Pc)是衡量各种设计目标在整个波形设计中所占的比重，因此可灵活调整各种设计目标在波形设计框架中的比重。

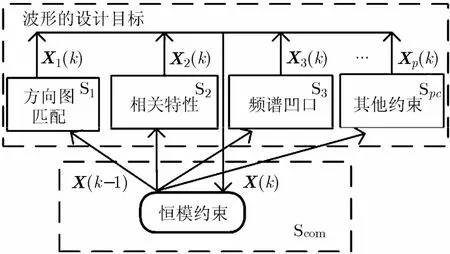
图 1 任意维迭代谱逼近算法的波形设计框架

3.2 投影算子的实现

本文对方向图匹配，指定区间良好的相关特性及频谱凹口等3种设计目标进行投影算子的实现，最终实现恒模波形的设计。

1为由协方差矩阵R所产生波形矩阵的集合，得到投影算子为

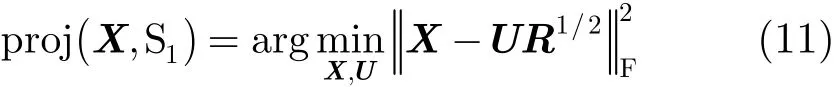
为了表示相关特性约束的集合[13]，p=1,2,…, 2N−1,m=1,2,…,M，定义集值函数(值为集合的函数)：

式中F1是具有合适尺寸的单位离散傅里叶变换矩阵，满足，则

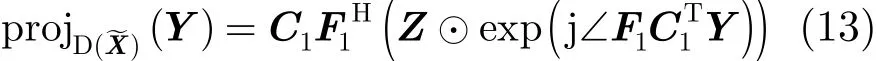
式中Z为理想波形的幅度，且Z∈ℝ2N×M。令S2= D，根据式(6)的定义，可令Z=G，根据式(6)，令，代入式(13)，即可得到指定区间相关特性的投影算子为

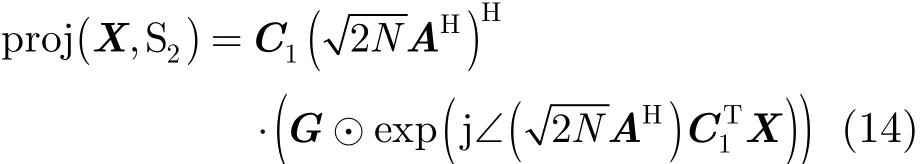
对于频谱凹口的目标函数进行投影算子的实现[13]，由式(8)可得，若每一列都在矩阵P的零空间，则式(8)的结果为零，因此假设矩阵P的零空间由矩阵QH的列张成，并定义集值函数为

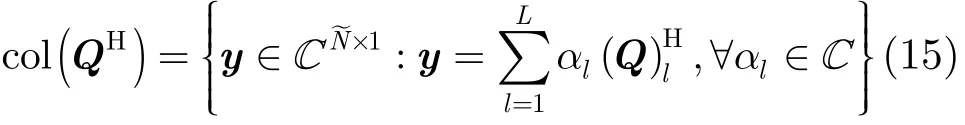
col(QH)为QH的列向量张成的子空间，L是频谱中保留的频率采样的个数，则向col(QH)的投影为

将矩阵Q转换为一个选择矩阵A和单位离散傅里叶变换矩阵F的乘积，即Q=AF, (AAH=IL×L, AHA=Diag(m))，定义向量m为

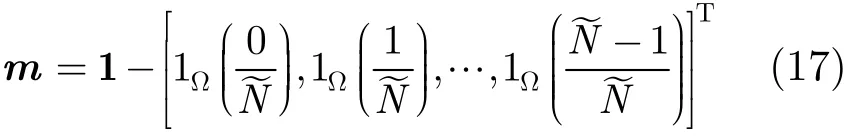
式中1Ω(⋅)是集合Ω的指示函数。代入式(16)，故矩阵X~可重新表述为

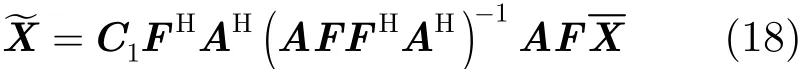
令S=col(QH)，可得频谱凹口约束的投影算子为

3

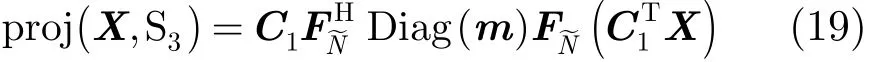
为了约束包络的幅度，实现恒模波形的设计[14,15]，定义集值函数为M(V)={X∈ℂN×M:, M(1)代表模值为全1恒模约束的集合，令

M(1)，最终可得到恒模约束的投影算子

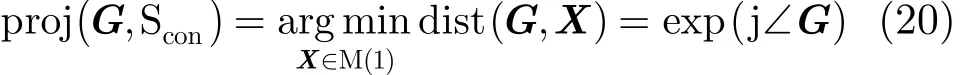
分别将式(11)，式(14)，式(19)和式(20)代入式(10)，即可得到本文所提出ADISAA算法的波形设计结果。

4 仿真结果分析

设MIMO雷达的发射阵元M=10，为标准的均匀线阵，阵元间距为半个波长，功率约束波形采样数N=256，功率约束c=M，即Rmm=M/M=1。波束中心为0°，波束宽度为60°。首先通过建模语言Cvxpy对方向图匹配的目标函数进行求解，得到与期望方向图对应的协方差矩阵R。为了量化方向图匹配的拟合效果[9]，设波形方向图与期望方向图之间的均方误差(Mean Square Error, MSE)为

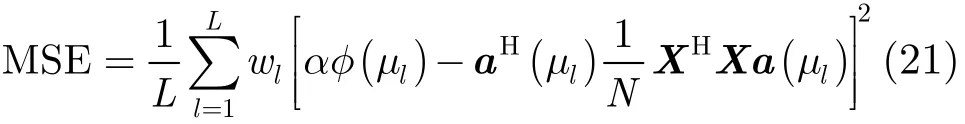
wl为期望方向图第l个采样点的权值，L为采样点数，α为比例因子。同时为了衡量指定区间相关特性的性能[6]，定义Rk为时延为k的波形协方差矩阵，则相关值(Correlation Level, CL)为CL=，另设是点的FFT,为频谱采样点数，频谱凹口的阻带旁瓣函数为

由于算法的复杂性、计算平台的差异性和不稳定性[16]，本文采用占用系统的内存量来直观地衡量算法的计算复杂度。

仿真1 不考虑频谱凹口的情况下，选择了方向图匹配、指定区间良好的相关特性等两种设计目标进行结合设计。设定Multi-WeCAN算法的指定区间参数，且γ0=3.0461。首先，为了明确权重对两种设计目标的影响效果，对其进行仿真分析，得到图2，作为新算法权重系数选择的依据。

本文的多功能波形优化设计优先考虑是方向图匹配，对于两种设计目标的优先级，设定方向图匹配大于指定区间良好的相关特性。由图2所示，当λ1≥0.7时，方向图匹配的均方误差变化趋势趋于平稳，λ2＜0.2时，指定区间的相关值变化陡降，因此选择λ1=0.7～0.8,λ2=0.15～0.30，其中λ1+λ2=1。

仿真2 与仿真1的仿真条件相同，对本文所提出的新算法和文献[9]的算法进行仿真(该算法采用了CA算法与发射方向图匹配进行结合设计，最终在恒模约束下实现波形设计)。设CA算法的指定区间参数P=5, λ1=0.8, λ2=1−λ1=0.2，得到以下仿真结果(图3)。

如图3(a)所示，在文献[9]所提出的算法中，方向图匹配的拟合均方误差MSE=3.20，在本文所提出的新算法中，方向图匹配的拟合均方误差MSE= 3.60。图3(b)表示在指定区间P=5的范围内，新算法的发射波形取得了约-53.07 dB的相关特性旁瓣深度，文献[9]的指定区间旁瓣深度为-38.05 dB。由此可见，与文献[9]所提出的算法相比，新算法的方向图匹配效果稍差，但取得10 dB以上指定区间相关特性旁瓣深度的增益。另外由仿真可得到文献[9]算法的占用内存为575156 kB，新算法的占用内存量为425416 kB，由于矩阵维数减少，有效减少算法的计算复杂度。

仿真3 考虑频谱凹口的情况下，设频谱采样点数N~=1000，归一化频率Ωs=[0.2,0.3]，设λ3为频谱凹口所对应的权重。由图2分析可得，可选择λ1=0.75, λ2=0.20, λ3=0.05作为实现3种设计目标同时设计的一种折中方案，并进行仿真实现，得到的结果如图4所示。

图2 权重与对应设计目标的效果曲线变化图

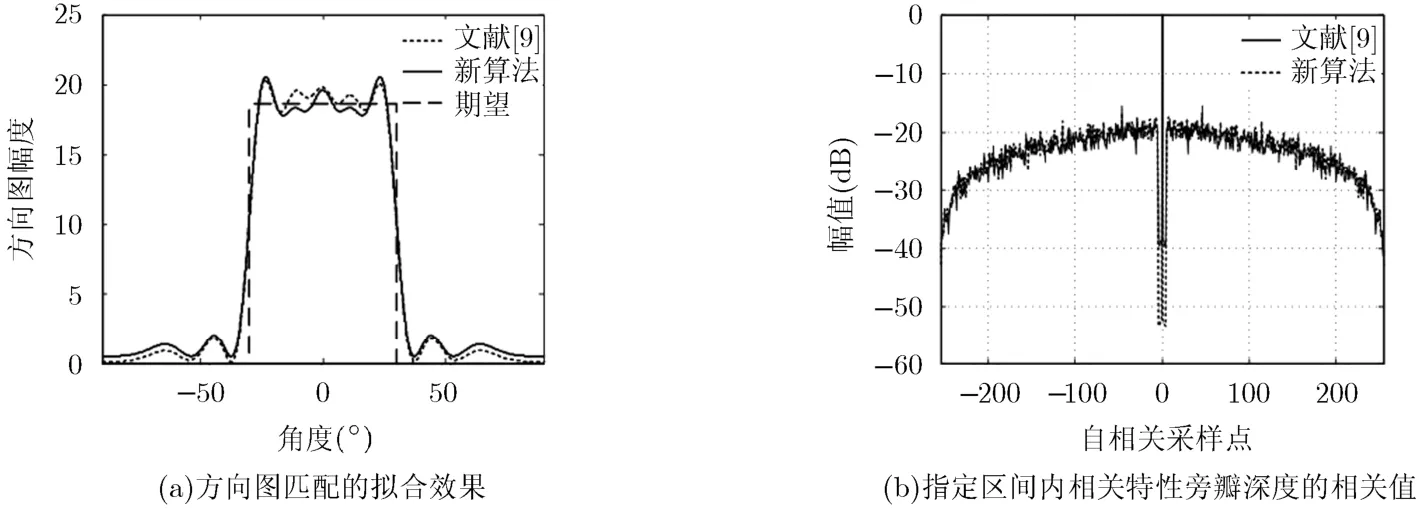
图3 综合两种设计目标的发射波形

由图4(a)可见， X为综合3种设计目标进行结合设计所得到的发射方向图，R为协方差矩阵R直接得到的发射方向图。与图 3(a)相比，由于λ1=0.75, X所对应的方向图拟合效果比文献[9]和仿真2的新算法稍差，具体表现为MSE=3.68，但与期望方向图进行对比，满足了方向图匹配的要求。由图4(b)与图3(b)进行对比，由于考虑频谱凹口，对信号的频谱进行展宽，从而影响了指定区间相关特性的性能，表现为CL=44.3 dB。由此可见，在结合3种设计目标进行设计的情况下，与仿真2的两种设计目标结合设计进行对比，指定区间相关特性旁瓣深度减少了9 dB左右，但与文献[9]进行对比，新算法在指定区间仍获得了5 dB以上相关特性的旁瓣增益，同时在阻带频段内(Ωs=[0.2,0.3])取得了-20 dB的功率谱凹口深度。

5 结束语

本文提出了一种集中式MIMO雷达多功能波形优化设计的框架，针对方向图匹配、指定区间良好的相关特性、频谱凹口设计等3种功能的设计目标进行结合设计，使用了一种ADISAA算法(任意维迭代谱逼近算法)来得到各个子设计目标的最优解，最终实现了恒模波形设计。仿真结果表明，虽然方向图匹配的拟合效果比文献[9]的算法稍差，但指定区间的相关特性取得5 dB的旁瓣深度增益，另外通过频谱凹口的设计，有效地避开了受到有源干扰和色噪声所污染的频段，并且减少了算法的计算复杂度，验证了算法的有效性。由于过程计算矩阵的维数都比较大，因此波形设计的内存占用量是一个有待于继续解决的问题。

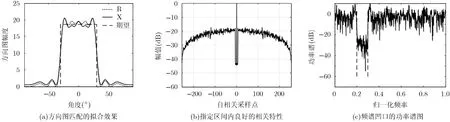
图4 综合3种设计目标的发射波形

[1] Daum F and Huang J. MIMO radar: snake oil or good idea? [J]. IEEE Aerospace and Electronic Systems Magazine, 2009, 24(5): 8-12.

[2] Li Jian and Stoica P. MIMO radar with colocated antennas [J]. IEEE Signal Processing Magazine, 2007, 24(5): 106-114.

[3] Li Jian, Stoica P, and Zheng Xia-yu. Signal synthesis and receiver design for MIMO radar imaging[J]. IEEE Transactions on Signal Processing, 2008, 56(8): 3959-3968.

[4] Fuhrmann D R and San Antonio G S. Transmit beamforming for MIMO radar systems using signal cross-correlation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(1): 171-186.

[5] 汤永浩, 马晓峰, 盛卫星, 等. 集中式MIMO雷达部分相关波形设计与处理[J]. 电子与信息学报, 2013, 35(6): 1471-1476.

Tang Yong-hao, Ma Xiao-feng, Sheng Wei-xing, et al.. Partially correlation waveform design and processing for co-located MIMO radar[J]. Journal of Electronics & Information Technology, 2013, 35(6): 1471-1476.

[6] He Hao, Stoica P, and Li Jian. Designing unimodular sequences sets with good correlations-including and application to MIMO radar[J]. IEEE Transactions on Signal Processing, 2009, 57(11): 4391-4405.

[7] Fuhrmann D and Antonio S G. Transmit beamforming for MIMO radar systems using partial signal correlation[C]. Proceedings of the 38th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, USA, 2004: 295-299.

[8] Li Jian and Stoica P. On probing signal design for MIMO radar[J]. IEEE Transactions on Signal Processing, 2007, 55(8): 4151-4161.

[9] He Hao, Li Jian, and Stoica P. Waveform Design for Active Sensing Systems[M]. New York: Cambridge University Press, 2012: 214-221.

[10] Xu Lu-zhou, Li Jian, and Stoica P. Target detection and parameter estimation for MIMO radar systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(3): 927-939.

[11] Sibui L H and Titlebaum E L. Signal design for detection of targets in clutter[J]. Proceedings of the IEEE, 1981, 69(4): 481-482.

[12] He Hao, Stoica P, and Li Jian. Waveform design with stopband and correlation constraints for cognitive radar[C]. Proceedings of the IEEE International Workshop on the Cognitive, Information Proceseing(CIP), Elba, USA, 2010: 344-349

[13] Zhao Yi-nan, Li Feng-cong, and Zhang Tao. Computational design of optimal waveforms for MIMO radar via multi-dimensional iterative spectral approximation[J]. Multidimensional Systems and Signal Processing, 2014, 46(22): 1456-1473.

[14] 赵宜楠, 张涛, 李风从, 等. 基于交替投影的MIMO雷达最优波形设计[J]. 电子与信息学报, 2014, 36(6): 1368-1373.

Zhao Yi-nan, Zhang Tao, Li Feng-cong, et al.. Optimal waveform design for MIMO radar via alternating projection[J]. Journal of Electronics & Information Technology, 2014, 36(6): 1368-1373.

[15] Cui Guo-long, Li Hong-bin, and Rangaswamy Muralidhar. MIMO radar waveform design with constant modulus and similarity constraints[J]. IEEE Transactions on Signal Processing, 2014, 62(2): 343-353.

[16] 胡亮兵, 刘宏伟, 杨晓超. 集中式MIMO雷达发射方向图快速设计方法[J]. 电子与信息学报, 2010, 32(2): 481-484.

Hu Liang-bing, Liu Hong-wei, and Yang Xiao-chao. Fast transmit beampattern synthesis for MIMO radar with colocated antennas[J]. Journal of Electronics & Information Technology, 2010, 32(2): 481-484.

陈志坤： 男，1982 年生，博士生，研究方向为MIMO雷达信号处理、电子侦察技术.

李风从： 男，1985 年生，博士生，研究方向为自适应信号处理、雷达统计信号处理.

乔晓林： 男，1948 年生，博士，教授，博士生导师，研究方向为极化雷达信号处理、电子对抗和反对抗技术.

赵宜楠： 男，1977 年生，博士，教授，博士生导师，研究方向为雷达统计信号处理、自适应波形设计.

Optimal Multi-function Waveform Design for MIMO Radar with Collocated Antennas

Chen Zhi-kun Li Feng-cong Qiao Xiao-lin Zhao Yi-nan
(School of Electronics and Information Engineering, Harbin Institute of Technology, Harbin 150001, China)

This paper addresses the simultaneous optimization problem of the multi-objective waveform design for MIMO radar with collocated antennas. Inspired from the idea of alternating projection, a waveform design framework is presented based on the Arbitrary-Dimensional Iterative Spectral Approximation Algorithm (ADISAA). Multi-objective of waveform design such as transmit beampattern match, good correlation, spectrum notch can be controlled by the adjustable weights. Finally, the constant modulus signal is designed. Simulation results show: the proposed algorithm improves the correlation performance of waveform at a specified lag intervals after transmit beampattern matching, the spectrum notch is designed to avoid the spectrum band which is polluted by active jamming and color noise, and it has lower computational complexity.

MIMO radar; Waveform design; Transmit beampattern match; Correlation performance

TN958

： A

：1009-5896(2015)06-1431-06

10.11999/JEIT141079

2014-08-14收到，2015-02-09改回

国家自然科学基金(61371181)资助课题

*通信作者：乔晓林 Chih_Quinn_Chen@yeah.net