基于中心-轮廓距离特征统计的形状表示方法

郭树旭 赵 静 李雪妍

(吉林大学电子科学与工程学院 长春 130012)

基于中心-轮廓距离特征统计的形状表示方法

郭树旭 赵 静 李雪妍*

(吉林大学电子科学与工程学院 长春 130012)

该文提出一种新的基于特征统计的形状描述方法。通过对中心-轮廓距离(CCD)和传统链码(Chaincode)的联合统计分析，使用中心-轮廓距离对形状进行层次分解，对各层的形状映射部分的链码描述进行统计分析，从而形成中心-轮廓距离和链码的联合统计(JSCCDC)描述子。形状之间的相似性可以用JSCCDC的城区距离来描述。实验结果表明，该表示方法兼具了形状的全局特征和局部特征，相比于传统的特征加权方法具有更优越的性能，在形状匹配和形状检索中具有较高的精度和可靠性。

模式识别；形状表示；特征统计；链码；中心-轮廓距离；匹配矩阵

1 引言

形状匹配与分类是模式识别与计算机视觉研究的重要问题，被广泛应用在很多领域，如目标识别、图像检索、人脸识别、医学图像诊断等，主要包括形状表示、形状匹配和度量学习3个模块。对于一个二值形状，先要提取其轮廓特征描述子，其区分能力的强弱将直接影响形状识别的结果，大多数形状匹配的工作都集中在此。匹配过程是找到一对不同形状之间的整体及局部的对应关系，对应关系的准确性也将会对之后得到的非相似度的区分能力产生直接影响。度量学习则是通过已知的数据库形状的上下文信息来改进原有距离度量的方法，这一步骤能将原有距离的区分性能大幅度提升[1]。

形状表示，又称特征提取或形状描述，是通过某种方法生成一个数值化的描述子来刻画形状特征的过程。轮廓特征描述子区分能力的强弱将直接影响形状识别与分类的结果，它是有效完成形状匹配任务的关键所在。形状特征描述子主要可以分为基于轮廓和基于区域两大类。基于区域的方法是利用物体内部区域(所有像素点)的信息来表示形状，而基于轮廓的方法主要是利用物体的边界轮廓信息来表示形状，与前者相比，其优势主要体现在对图像低层特征的高识别度以及相对较小的计算量上。因此，该方法成为近年来形状表示研究的主流。

基于轮廓的形状表示方法大致可以分为4类：全局描述子，局部描述子，多尺度描述子和多方面描述子。早期描述子，如边界长度、直径、圆度等都属于全局描述子。全局特征一般是平移，旋转不变的，计算简单，但仅仅只能表示形状的大致特性，缺少细节描述，区分力不足。为此部分学者提出了局部形状描述子的概念，如链码和形状显著性描述符(Shape Salience Descriptor, SSD)[2]，此类描述子对形状进行了细致刻画，但对噪声非常敏感。针对这一问题，出现了多尺度描述子，如文献[3]提出的多尺度分形(Multi-Scale Fractal, MS Fractal)维数算法和文献[4]提出的用轮廓点控制尺度的算法。此外还有以文献[5]提出的以形状上下文为代表的多方面描述子，通过轮廓点的空间位置关系和分布来反映形状特征。近年，还有部分学者提出了特征统计的方法，如同心离散圆簇描述法[6]。

单一特征描述子无法胜任复杂可变形状的识别工作。如链码是一种用曲线起始点的坐标和边界点方向代码来描述曲线或边界的方法，但其编码只依赖于轮廓序列中相邻点的相对位置信息，无法体现轮廓的全局特征，且码串长，在传输的过程中易受干扰。中心距离函数[7]是将轮廓线上的点到形状的几何中心的距离描述成中心角度的函数，这种方法一般能够重构被描述的形状，但当形状的几何中心位于形状区域之外或者被描述形状过于复杂时，就可能出现一个中心角对应多中心距的情况，为了能将其转化成1维函数，通常对这些多值有所取舍或者求取平均值，但无论怎样取值，都造成了形状信息的丢失从而不能重构，无法满足形状描述的唯一性[8]。中心轮廓距离曲线(Centroid Contour Distance Curve, CCDC)[9]虽然克服了中心距离函数一个中心角对应多个中心距的问题，但由于数字图像量化定义的弧长精度，CCDC对形状轮廓各部分的描述精度及所占带宽随着其像素的增加而递增，因此抗噪性弱，且无法重构图像。

针对上述问题，本文从特征统计方法入手，融合了链码在局部描述方面的优势和中心-轮廓距离(Centroid-Contour Distance, CCD)对全局特征刻画的优势，提出基于中心-轮廓距离和链码的联合统计(Joint Statistical of Centroid-Contour Distance and Chaincode, JSCCDC)描述形状的新方法：通过使用CCD对形状进行层次分解，对映射到每一层的形状的链码描述进行统计分析，从而得到形状的JSCCDC特征。实验证明JSCCDC能够很好地表达形状的全局与局部特征，相较于传统的形状表示方法更有效。

2 链码的统计特征

2.1 统计链码

由于链码在形状匹配中无法克服旋转、噪声和目标尺度变化带来的一系列问题，文献[10]提出一种基于Freeman链码的形状描述方法：最小和统计方向码(Minimum Summation Statistical Direction Code, MSSDC)。这种方法虽然在一定程度上实现了对形状的固定或者相似角度的观察，但由于噪声或者柔性形变引起的变化，在进行形状匹配时，并不能保证以两者最相似的视角进行匹配。为此，本文将在2.2节提出匹配矩阵的概念。

基于文献[10]，对于给定的形状链码表示，本文给出N-方向的归一化的统计链码S形式：

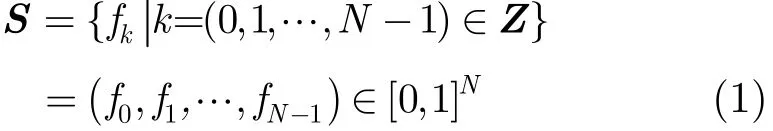
其中，fk表示码元k出现的频率，根据定义可知，S满足归一化条件。

2.2 匹配矩阵

为了实现统计链码的最佳匹配，本文定义了N阶匹配矩阵M来匹配N-方向统计链码：

匹配矩阵M的每行每列分别对应着形状旋转和翻转一定角度后的形态，角度精度由链码的方向数N决定。应用匹配矩阵的统计链码匹配流程为：

(1)首先，给出两个待匹配形状A和B的统计链码形式SA和SB；

(2)其次，计算基于SB的匹配矩阵：

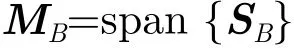
(3)再次，根据式(3)计算SA在匹配矩阵上的投影系数矩阵Q。

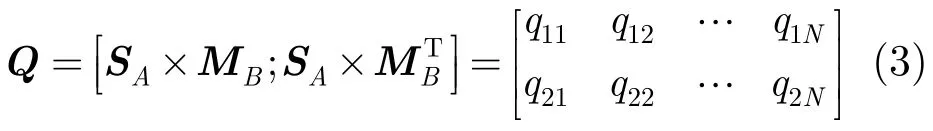
找到投影系数矩阵Q的最大值并标记其所在的行(第a行)和列(第b列)，如式(4)所示。

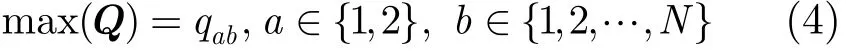
在式(3)中，Q是本文定义的基于匹配矩阵M的投影系数矩阵，以SA和MB构造的投影矩阵为例，Q中的每个元素对应的是形状A与不同角度观察到的形状B的相似程度。

(4)根据最小二乘原理，本文认为使投影系数矩阵Q取得最大值的MB的行或者列是与待匹配形状A最相近的视角观察到的形态的统计链码表示，记为

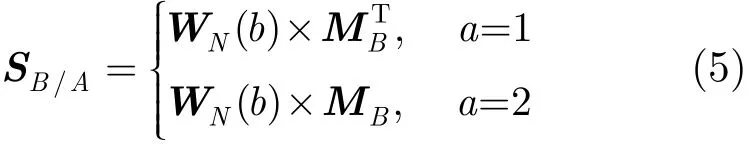
式(5)中，a和b是式(4)中标记的Q的最大值的行列位置，WN(b)定义如式(6)所示。

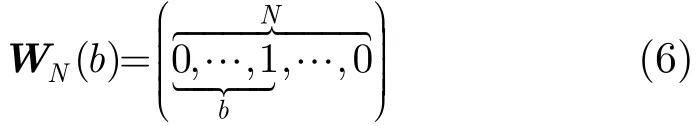
(5)最后，使用L2范数计算SA和SB/A的距离，如式(7)所示，Ds的值越大，则表示形状A和B的相似度越低，显然，Ds(A,A)=0。

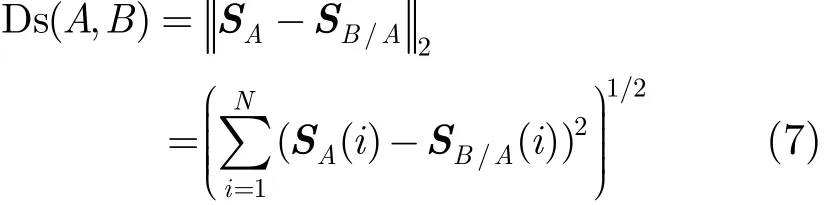
3 中心-轮廓距离(CCD)的特征统计

3.1 基于CCD的传统描述

传统的基于CCD的形状描述方法主要有中心距离函数和中心轮廓距离曲线(CCDC)。中心距离函数将轮廓上的点到形状几何中心的距离描述成中心角度的函数，量化时会舍去部分点的信息；CCDC用序列号取代中心角的方案解决了轮廓点取舍的问题，却也相当于根据轮廓的周长对其进行加权，这与人们平时的视觉处理方式不一致，降低了抗噪性，给匹配带来了困难。

3.2 极半径——统计CCD

由于CCD的尺度不变特征，对其进行角度化处理可能损失部分点的信息，如中心距离函数，而CCDC却由于序列的等间隔性天然地根据周长对CCD进行了加权而引入了匹配过程难以复原的尺度信息，需要对CCDC做分段切割处理，也相当于是一种角度化处理的过程。为了克服上述针对CCD角度化引起的问题，本文提出幅度化的概念，即对CCD的幅值进行统计分类的过程。

(1)本文给出形状几何中心的定义：

(io, jo)是目标形状轮廓的几何中心，图像大小是m×n, f(i,j)是边界坐标(i,j)灰度值，对于二值图象，f(i,j)取值只可能是“0”或者“1”。

(2)首先，顺时针找出目标形状的边界坐标，记做C={(i,j)|f(i,j)≠0}={(i1,j1),(i2,j2),…}。

(3)根据(io, jo)和C给出形状的CCD串，为了区别于是其他基于CCD的描述子，本文定义使用的CCD为极半径R：

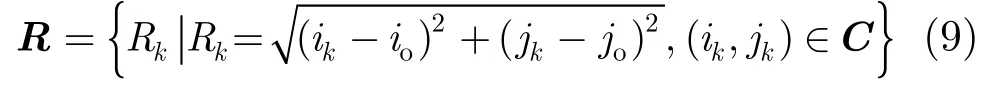
(4)其次，把统计的思想应用到R中，确定精度L后，给出分段步长：

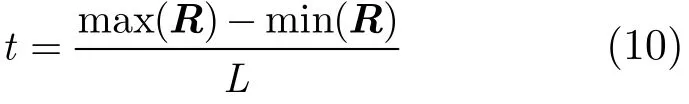
(5)根据t给出统计极半径的定义：

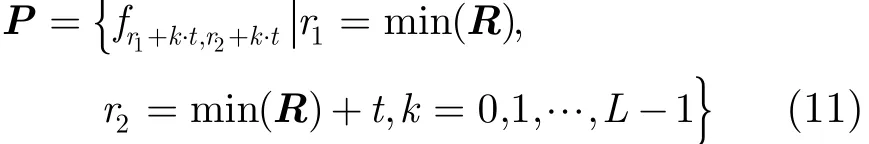
式(11)中，fr1+k⋅t,r2+k⋅t是极半径R落在[r1+k·t,r2+k·t]区间的的频率，即把形状质心映射到一个内径为r1+k·t，外径为r2+k·t的圆环中心，统计圆环内目标形状的弧长总和，再利用形状的周长进行归一化得到极半径在当前区间的出现频率。通过精度确定的步长t来定义圆环宽度，遍历整个极半径区间则得到定义的统计极半径。

(6)最后，同样采用L2范数来定义不同形状的统计极半径的距离：

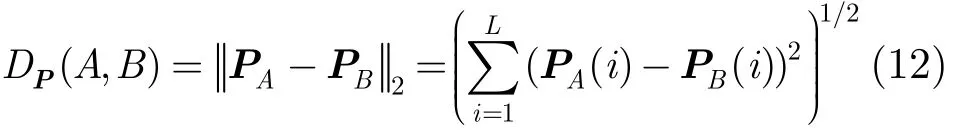
4 CCD和链码的联合统计

针对统计链码和统计极坐半径，为了结合它们在形状描述方面各自的优势，本文提出了联合统计。

4.1 链码和极半径的联合统计描述

首先，本文在Freeman链码的基础之上进行改进，在原始链码中加入了极半径信息，获得链码-极半径的联合描述子，定义如下：

其中，F是对形状A的轮廓进行Freeman编码的结果，R是对应的编码点的极半径，可根据式(9)求得。

定义链码和极半径的联合统计描述子(JSCCDC), JSCCDC在统计链码的同时也统计极半径空间位置，其形式为

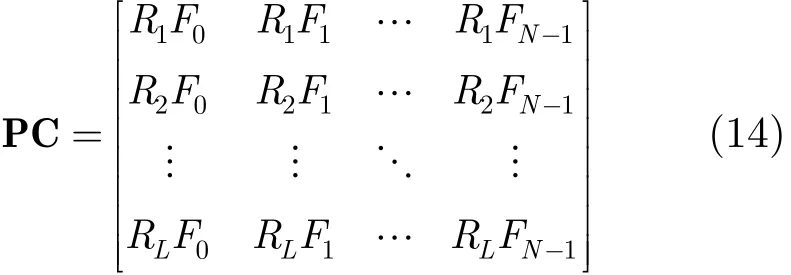
元素RiFj表示的是在第i个极半径空间中坐落的j方向的矢量线段的概率。N是N方向Freeman链码，L是对极半径区间的L等分。如图1(a)所示的蝙蝠轮廓，首先设定参数L=8, N=8，然后根据式(8)标记其几何中心，并根据式(9)和值确定分段步长t，画出等分圆环。最后统计落在每一个圆环内的轮廓的链码分布，并对整个轮廓进行归一化，即可得到式(14)中的PC矩阵，也就是形状的JSCCDC描述，如图1(b)所示。

4.2 JSCCDC匹配

图1 JSCCDC描述子

JSCCDC是一种矩阵描述。本文借鉴图像处理中像素间的城区距离(即模为1的距离)来描述两个矩阵的相似性，即利用式(15)分别计算两个矩阵对应位置的差，取其绝对值和为两个矩阵的距离。同时，也借鉴了文献[8]中距离测量公式，即分别对矩阵的每行以L2范数来衡量其差异度，最后把各行差异度的平方和作为矩阵差异度，定义如式(16)。在5.1节的相似性评测实验中，为了和文献[8]的方法比对，本文采用与其相同的距离测量，即式(16)，但时间复杂度较高，在检索实验中使用城区距离来计算。

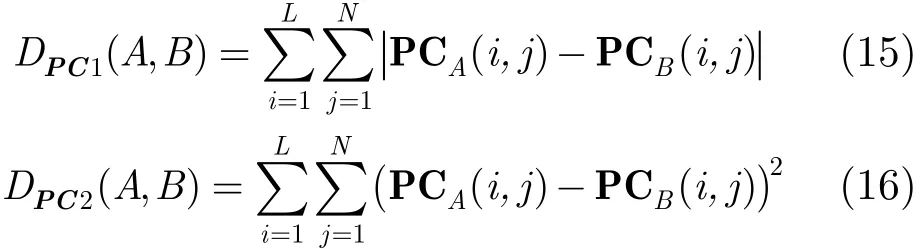
为了实现匹配的鲁棒性，对矩阵PC的行向量引入式(2)的匹配矩阵，以实现JSCCDC描述子对平移、旋转、翻转和尺度变换的鲁棒描述。

5 实验

5.1 相似性实验

本文选取了MPEG7 CE-Shape-1形状数据库中的Hammer图像，对其进行了如图2所示的各种变换，并随机从MPEG7 CE-Shape-1选取了图3所示的其他形状作为类间形状对比，给出了不同方法下形状的类间类内距离测度。实验参数：N=8, L=8。

表1给出了使用JSCCDC结合匹配矩阵方法测得的图2和图3中图例的类内类间距离。通过类内距离来看JSCCDC的表征能力，不仅能够实现对平移、旋转和尺度变换的鲁棒性，由于匹配矩阵的引入，还能还原形状的翻转变换。但由于数字图像的量化问题，对形状的旋转和尺度变换还原还有一定的误差。

结合类间距离再来看JSCCDC的分类能力：JSCCDC测得的Hammer形状的类内距离落在[0,0.0024]，狭义类间距离(类内测试形状与其他形状的距离)落在[0.0255, 0.0376]，广义类间距离(类间形状的相互距离)落在[0.0092, 0.0408]，与类内距离无交集，可以实现形状分类。本文将分类能力定义为广义类间距离与类内距离的比值，由此得出JSCCDC对Hammer形状的分类能力为47.6。

图2 Hammer形状的10种变形

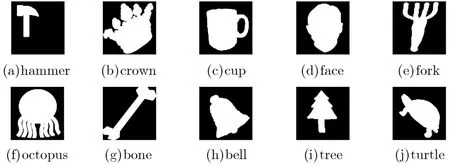
图3 节选自MPEG7的类间形状示例

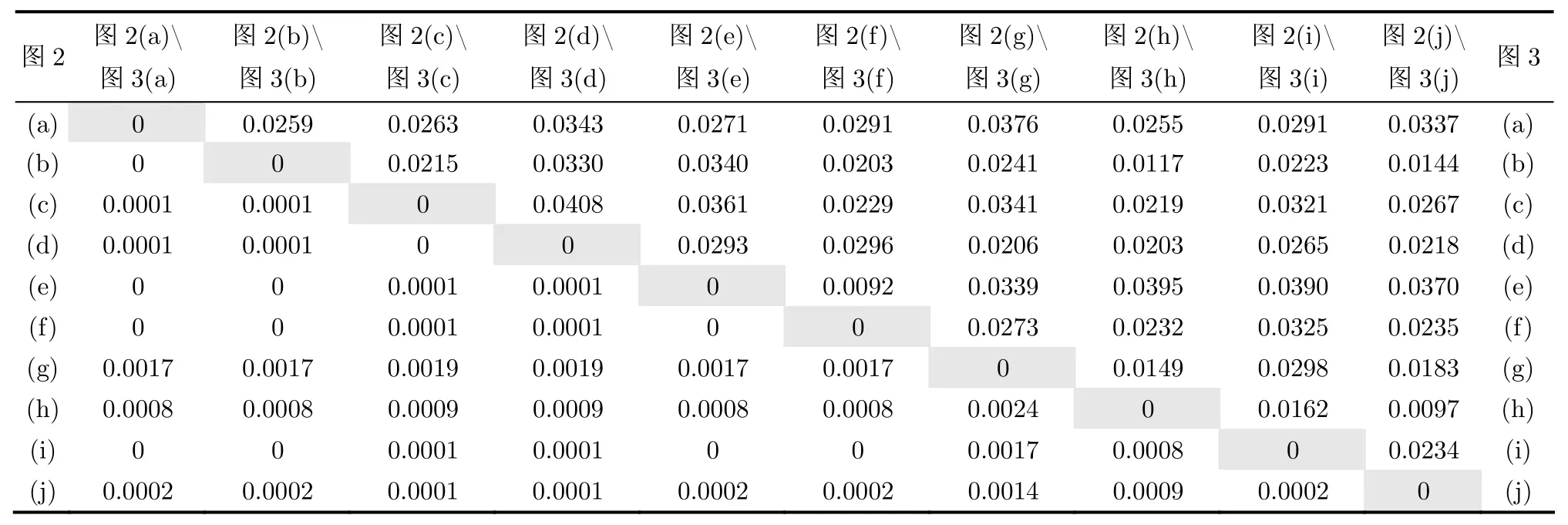
表1 JSCCDC测得的类内类间距离

表2 不同算法相似度评测对比

表2是其他算法在相似度实验中和本文方法的各类指标比较。可以看出，JSCCDC在相似性评测方面的性能是优于很多传统算法的。为了测试实验的普遍性，本文对图3中的其他形状均进行了图2所示的各种变换，代替Hammer形状重复上述相似性实验过程，得到了一个均值统计，表2最后一列所示。

5.2 形状检索实验

5.2.1 MPEG-7数据库 MPEG-7 CE-Shape-1数据库是由文献[11]在2000年发布的，共包含3个部分，其第2部分主要用来衡量基于相似性方法的检索精度，是目前衡量形状描述子的重要参考指标之一。它包含70个类别、每类20幅不同形态共1400张形状图像，如图4(a)和图4(b)所示。使用Bull-eye方法度量检索精度，对每一幅图像检索出最相似的40幅图像，检索率R可通过式(17)计算，其中，T(j)表示检索出的与第j幅待检形状同一类形状的个数。

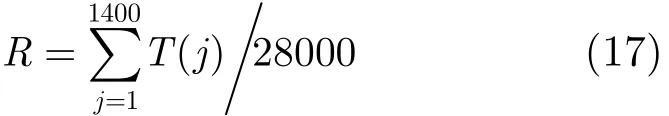
表3是本文算法和部分经典算法在MPEG-7数据库上的检索率。其中，Fourier是经典的傅里叶描述子[12]，CS是一种基于轮廓显著(Contour Salience, CS)的描述[13]，MSSDC是2.1节提到的最小统计和方向码，MI是一种基于不变矩(Moment Invariant, MI )的描述[14]，MS Fractal是一种多尺度分形描述，SSD是一种基于局部距离函数的形状显著性描述子，SSD+GF是加入全局特征(Global Feature, GF)的SSD描述子[2]，JSCCDC+M是应用匹配矩阵的JSCCDC描述。对比3和5以及9和10两组数据，本文提出的匹配矩阵在统计链码的匹配中实现了有效的对齐，检索率都有所提高。虽然相较于加入全局特征的SSD描述子，JSCCDC在检索率表现方面略逊一筹，但对比5和10以及8和11两组数据，本文在统计链码基础之上加入全局特征而提出的JSCCDC描述子提高了统计链码的检索率绝对值达0.28，高达70%，而加入全局特征的SSD描述子在原有基础之上提高了0.10，只有16%，可以看出本文提出的联合统计的方法较传统的特征引入法更能改善描述子性能，因此，JSCCDC这种多特征联合统计的描述方法在形状检索工作中更具优势。

5.2.2 Kimia99数据库 Kimia99数据库由文献[16]提出，共包含9类形状，每一类11个子形状，如图4(c)所示。这些形状中不仅同类形状有局部的变形，还有局部的遮挡，且不同形状甚至还有相似的全局特征。

Kimia99数据库通用的评价标准通常以表格的形式呈现，数据库中的每一个图像都要作为模板对全库进行检索。表4是本文方法和部分其他经典算法的对比，其中SP加权法是本文提出的统计链码和统计极半径平均加权的方法。可以看出JSCCDC的正确识别率不仅优于其他经典的基于单一特征的形状描述子，而且效果优于特征加权方法。

图4 本文引用数据库图例

表3 不同算法在MPEG-7数据库上的检索率

5.3 时效性分析

实验条件：硬件为AMD Athlom(tm)ⅡX2 250 Processor, RAM= 4 GB；软件为Win7, 64位操作系统，MATLAB；数据库为MPEG-7(1400幅，gif格式)，Kimia99(99幅，pgm格式)。

5.1 节的相似性实验和5.2节的检索实验证明了JSCCDC这种联合统计描述子在形状表示方面的优越性，为了进一步验证该算法是否具有实际应用价值，特别设计了时效性实验，主要对比基于链码的各种描述子在MPEG-7数据库和Kimia99数据库上的检索时间和性能，为了体现基于轮廓描述法在处理时间上的优越性，特别加入了基于区域的10阶Zernike矩算法进行对比。实验结果如表5所示。JSCCDC处理速度稍逊统计链码，仍优于MSSDC算法，但检索性能却较两者有大幅度提高。

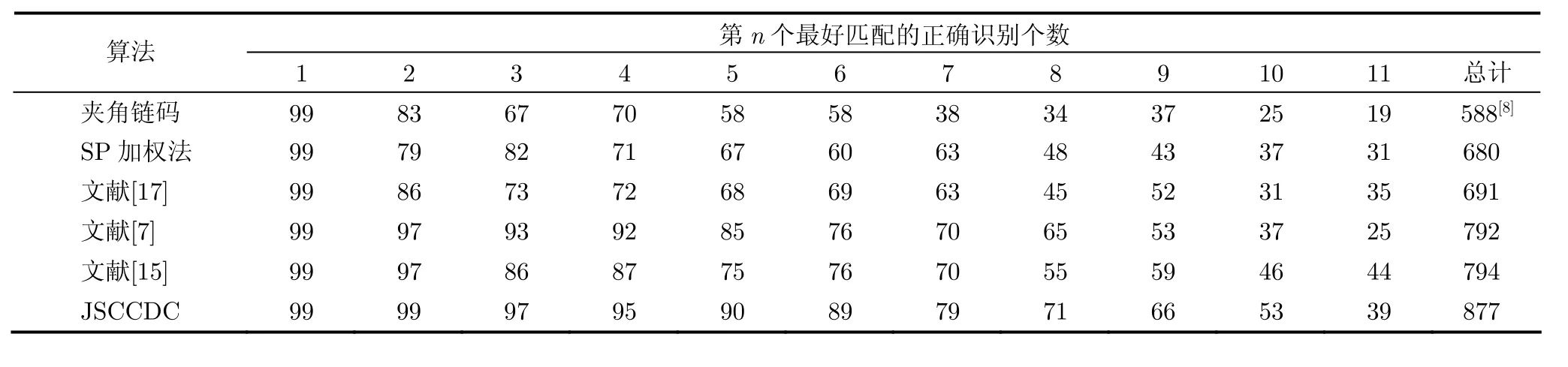
表4 部分算法在Kimia99数据库上的检索效果

6 结束语

本文提出了一种新的基于形状中心-轮廓距离和链码联合统计的形状描述和匹配方法。首先，它通过中心-轮廓距离对形状进行层次分解，然后统计每一层形状映射部分的链码描述，从而形成了中心-轮廓距离和链码的联合统计(JSCCDC)。这种描述方法通过对形状的两种简单特征的联合统计，既描述了形状的局部特征，又包含了全局信息。经典数据库上测试结果表明，这种联合统计的方法不仅优于单一特征描述法，而且优于加权方式结合的局部-全局特征描述。

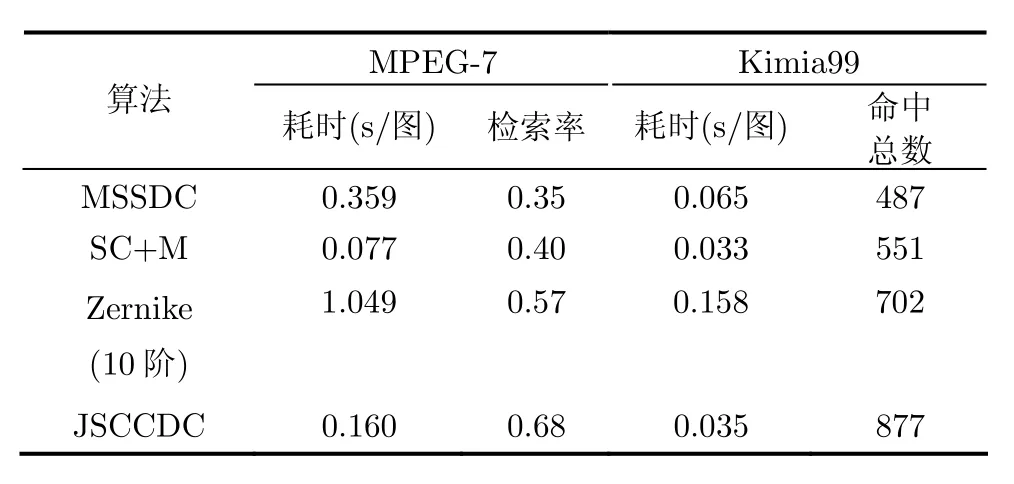
表5 部分链码算法在Kimia99和MPEG-7数据库上性能对比

[1] 周瑜, 刘俊涛, 白翔. 形状匹配方法研究与展望[J]. 自动化学报, 2012, 38(6): 889-910. Zhou Yu, Liu Jun-tao, and Bai Xiang. Research and perspective on shape matching[J]. Acta Automatica Sinica, 2012, 38(6): 889-910.

[2] Glauco V P, Marcos A B, and Celia A Z B. Image feature descriptor based on shape salience points[J]. Neurocomputing, 2013, 120(23): 156-163.

[3] Torres R S, Falcão A X, and Costa L F. A graph-based approach for multiscale shape analysis[J]. Pattern Recognition, 2004, 37(6): 1163-1174.

[4] Alajlan N, Kamel M S, and Freeman G H. Geometry-based image retrieval in binary image databases[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2008, 30(6): 1003-1013.

[5] Belongie S, Malik J, and Puzicha J. Shape matching and object recognition using shape contexts[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2002, 24(4): 509-522.

[6] 孙景乐, 唐林波, 赵保军, 等. 改进的同心离散圆簇形状描述方法[J]. 电子与信息学报, 2013, 35(8): 1901-1906. Sun Jing-le, Tang Lin-bo, Zhao Bao-jun, et al.. An improved shape descriptor of cluster of concentric discrete circles[J]. Journal of Electronics & Information Technology, 2013, 35(8): 1901-1906.

[7] Bernier T and Landry J A. A new method for representing and matching shapes of natural objects[J]. Pattern Recognition, 2003, 36(8): 1711-1723.

[8] 王斌, 舒华忠, 施朝健, 等. 一种基于轮廓线的形状描述与匹配方法[J]. 电子与信息学报, 2008, 30(4): 949-952.

Wang Bin, Shu Hua-zhong, Shi Chao-jian, et al.. A contour-based shape description and matching method[J]. Journal of Electronics & Information Technology, 2008, 30(4): 949-952.

[9] Wang Zhi-yong, Chi Zhe-ru, and Feng Da-gan. Shape based leaf image retrieval[J]. IEE Proceedings-Vision, Image and Signal Processing, 2003, 150(1): 34-43.

[10] 王小玲, 谢康林. 一种新的方向码描述的图像检索方法[J]. 哈尔滨工业大学学报, 2006, 38(9): 1545-1548.

Wang Xiao-ling and Xie Kang-lin. Novel shape-based image retrieval using direction code[J]. Journal of Harbin Institute of Technology, 2006, 38(9): 1545-1548.

[11] Latecki L J, Lakaemper R, and Eckhatdt T. Shape descriptors for non-rigid shapes with a single closed contour[C]. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Hilton Head Island, USA, 2000: 424-429.

[12] Zhang Deng-sheng and Lu Guo-jun. Shape-based image retrieval using generic Fourier descriptor[J]. Signal Processing: Image Communication, 2002, 17(10): 825-848.

[13] Torres R S and Falcão A X. Contour salience descriptors for effective image retrieval and analysis[J]. Image Vision Computing, 2007, 25(1): 3-13.

[14] Liao S X and Pawlak M. On image analysis by moments[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1996, 18(3): 254-266.

[15] Nacéra L, Slimane L, Farouk L, et al.. Curve normalization for shape retrieval[J]. Signal Processing: Image Communication, 2014, 29(4): 556-571.

[16] Sebastian T B, Klein P N, and Kimia B B. Recognition of shapes by editing their shock graphs[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2004, 26(5): 550-571.

[17] 王斌. 一种用于形状描述的拱高半径复函数[J]. 电子学报, 2011, 39(4): 831-836. Wang Bin. Shape description using arc-height radius complex function[J]. Acta Electronica Sinica, 2011, 39(4): 831-836.

郭树旭： 男，1959年生，博士，教授，研究方向为图像处理与信号分析.

赵 静： 女，1989年生，硕士，研究方向为图像处理与模式识别.

李雪妍： 女，1980年生，博士，讲师，研究方向为图像理解与模式识别.

Research on Shape Representation Based on Statistical Features of Centroid-contour Distance

Guo Shu-xu Zhao Jing Li Xue-yan
(College of Electronic Science and Engineering, Jilin University, Changchun 130012, China)

This paper proposes a novel shape representation method based on statistical features. According to the joint analysis on Centroid-Contour Distance (CCD) and chaincode, the silhouette is decomposed into several levels based on CCD. And then, the chaincode describing laying in each level is analyzed to extract the Joint Statistical of Centroid-Contour Distance and Chaincode (JSCCDC) descriptor for the silhouette. The similarity between different shapes can be measured by the city-block distance. Experiment results show that the proposed method describes both global and local features. Compared with traditional feature weighting method, JSCCDC is more accurate and reliable for shape matching and retrieval.

Pattern recognition; Shape representation; Feature statistics; Chaincode; Centroid-Contour Distance (CCD); Matching matrix

TP391.4

： A

：1009-5896(2015)06-1365-07

10.11999/JEIT140960

2014-07-21收到，2015-01-15改回

*通信作者：李雪妍 leexy@jlu.edu.cn