浅析算法及其应用研究

郭梅

（石河子大学机械电气工程学院，新疆石河子832003）

浅析算法及其应用研究

郭梅

（石河子大学机械电气工程学院，新疆石河子832003）

随着计算机应用技术的快速发展，智能算法在工程设计规划领域的重要性不言而喻。本文将PSO算法与工程数学、机构设计优化相结合，通过对PSO算法的初始化参数设置和适应度函数的选取进行全局最优解的求取。结果表明，PSO算法能够快速准确进行复杂工程设计问题的求解。

PSO算法；工程数学；机构优化设计

当前工程设计技术快速发展，传统的优化设计方法在解决线性规划、非线性规划、整数规划、几何规划和动态规划问题中，因其建模难度大、数学模型描述能力低、误差大，其求解能力有限、难以处理复杂和形态不好的问题，难以求得全局最优解，因此可将计算机智能算法应用到工程规划设计和其他各领域的优化求解过程中。

粒子群算法（Particle Swarm Optimization，PSO）作为一种崭新的随机搜索算法，目前已开始应用于诸多领域，比如化工系统、电力系统、生产调度和机械设计等方面，其在多目标、约束和动态等问题优化上的研究已逐渐被人们重视。如龚松建等[1]利用PSO算法结合最小二乘支持向量机（LS-SVM）对未来1 h风速进行预测，模型的预测精度较高、运算速度快。李小为等[2]以六自由度机械臂的运动学正逆解为前提，为使其在不同速度约束下均能够以最短时间运行，提出了PSO优化速度约束下的时间最优3-5-3多项式插值轨迹规划方法。同时PSO算法通用性强、所需调整的参数少、容易实现、收敛速度快，能够满足复杂工程设计要求。

本文通过对PSO算法的研究，在标准PSO算法的基础上采用惯性权重模型提高了算法的全局搜索能力。以工程数学和机构优化设计为例，采用PSO优化算法进行全局最优解的求取，求解结果准确快速。

1 PSO算法简介

PSO算法是由Kennedy和Eberhart共同开发[3]，起源于对鸟群的捕食行为研究，根据群体中个体信息共享使得群体运动在问题求解空间中由无序变得有序，获取全局最优解。其具体步骤如下：（1）初始化粒子群中各微粒的速度、位置、加速常数、最大迭代次数、惯性因子和算法终止的最小允许误差。如果当前搜索空间为d维，则每个微粒中包含d个变量，并将各微粒当前历史最优位置Pbest设置为初始位置，取群体全局最优位置为gbest中最优值。（2）计算各微粒的适应度，将最佳适应值作为当前的全局最优值，并将最佳适应值对应的位置作为全局最优值所在的位置。（3）更新每个粒子当前的飞翔速度，并约束每个微粒的飞翔速度，使其不能超出所设定的最大飞翔速度值。（4）更新每个粒子当前所在的位置，比较当前每个粒子的适应值是否比历史局部最优值好，如果好，则将当前粒子的适应值即为局部最优值，其对应的位置作为每个粒子群的局部最优值所在的位置。同时在当前群中找出全局最优值，并将此时全局最优值对应的位置定为群体全局最优值所在位置。（5）重复步骤3～4，直到满足预先设定的最小允许误差或最大迭代次数。（6）输出粒子群全局最优值和其对应的位置以及每个粒子的局部最优值和其对应的位置。

2 PSO算法的参数选取与算法改进

在基本粒子群算法中，粒子数m、最大飞翔速度νmax、惯性因子ω和加速常数c1与c2等几个参数对算法寻优性能的影响非常显著，因此通常采用对这些参数的调节来改进PSO算法。

粒子数m的取值一般为20～40。经大量试验结果表明，粒子数越多，其搜索范围越大，越容易找到全局最优解，然而算法运行的时间也越长。对于多数问题，粒子数定为30即可，但相对于特殊问题粒子数需100～200。

对于简单的问题，一般情况下加速常数c1=c2=2.0。目前对于加速常数c1和c2的确切取值，各学者观点并不完全相同，表1所列是几位主要研究学者给出的参考值[4]。c1与c2常被用来调整个体经验和社会经验在粒子运动过程中的作用权重，如果c1= 0，c2≠0，则粒子没有自身经验，只有社会经验，对于相对复杂问题，求解过程陷入局部最优的可能性较大。如果c1≠0，c2=0，则粒子群只有自身经验，没有社会经验，由于各微粒之间没有实现信息的共享，粒子群m的搜索行为相当于m个单个粒子在单独运行，因此获取最优解的概率非常低。如果c1=c2=0，则粒子将一直无序地飞往边界，因此只能搜索有限区域，很难找到最优结果。

表1 加速常数参考值

惯性因子ω对于粒子群算法的收敛性起到很大作用，ω值越大，粒子飞翔幅度越大，粒子容易离开原先寻优轨道，在更大的空间进行搜索，致使失去局部的寻优能力，而全局搜索能力越强；ω值越小，则局部寻优能力增强，加快了算法收敛，提高了搜索精度，其全局寻优能力变得越弱。通常在迭代初始时将ω设得较大，在随后的迭代过程中逐渐减小，使得粒子群在初始优化时搜索空间较大，并得到合适的种子，后期逐步收缩至较好的解空间进行更为精细搜索，从而使其成为兼顾全局搜索和局部搜索的一个折中。若ω为变量，可取0～1的随机值，若ω为定值，可取0.60～0.75合适值。

在粒子群算法运行过程中，粒子速度的改变是随机的，容易造成粒子在问题空间搜索的无休止进行。为使粒子进行有效搜索，可使其搜索过程中振幅衰减。传统的方法是使用一个参数最大飞翔速度νmax对粒子运动速度进行限制，从而防止粒子群搜索范围的无序发散和因速度过大而越过最优目标。同时粒子群为跳出局部最优，可将寻优步长增大，当接近最优值时，再将步长减小。若νmax固定不变，常设为每维变化范围的10%～20%。

3 PSO算法在工程数学中的应用

在工程数学求解时，传统的计算方法已逐渐不能适应大数学快速准确计算要求，并且计算的结果常出现错误，为获取快速精确的计算结果，本文尝试将PSO算法思路引用到工程数学计算中。

在利用PSO算法求解Max f（x）=2.1×（1-x+ 2×x.ˆ2）.×exp（-x.ˆ4/2），x∈[-5，5]的全局最大值时，将PSO初始化参数设置如下：最大允许误差为0.001，粒子群规模为100，个体学习因子为2，社会学习因子为2，惯性因子为0.6，最大飞翔速度为0.8。通过算法计算结果如图1所示，可知在x取值为-0.871 36时，该函数取得最大值5.336 1，整个计算过程耗时0.279 3 s，计算结果精确到小数点后4位。其计算结果与传统求解的正确答案一致，然而我们正常求解的耗时却需耗费月30min，大大提高了工作效率。

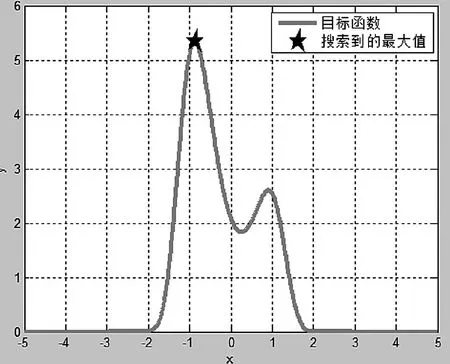
图1 PSO算法搜索函数最大值

4 PSO算法在机构优化中的应用

在机械结构设计过程中，经常涉及到结构优化问题，该类问题也可以通过软件实现，如采用复合形法、随机方向阀或者优化工具箱法，本文尝试将PSO智能算法与平面四杆机构的优化问题相结合获取最优解。

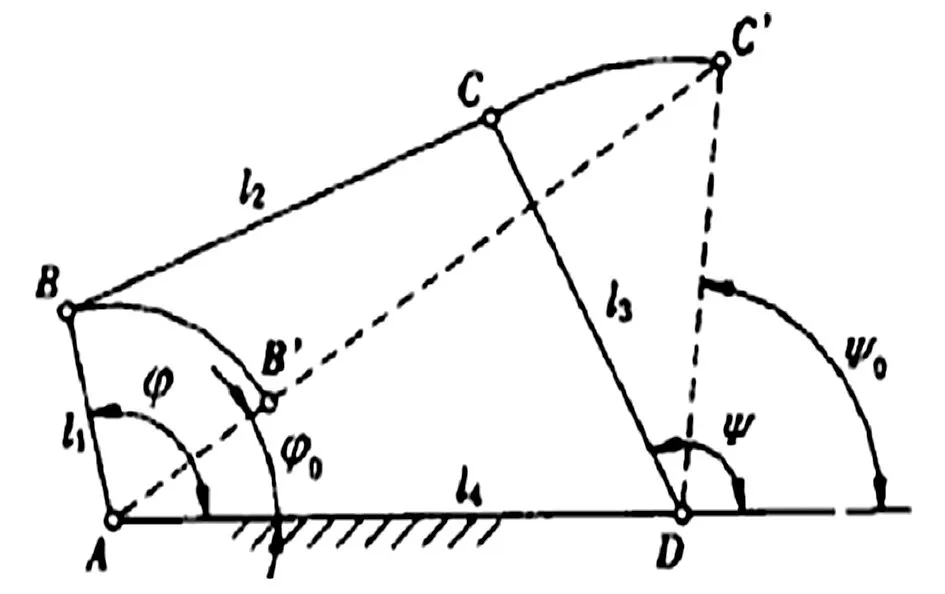
图2 平面四连杆机构极限位置

如图2所示的平面连杆机构，当原动件曲柄的转角φ在φ0～φ0+90°时，要求从动件摇杆的输出角能实现函数Ψ=Ψ0+[2/（3π）]×（φ-φ0）2。其中φ0、Ψ0分别为对应摇杆在右极限位置时，曲柄和摇杆的初始位置角，以水平机架方向逆时针计量，要求机构传动角范围45°≤γ≤135°，曲柄长度设为l1=1，机架长度设为l4=5。

为了使机构传力性能良好，机构传动角范围45°≤γ≤135°，即要使得c o s 1 3 5°；整理后得到约束方程:0；同时为满足曲柄存在的杆长和条件，l2≥l1，l3≥l1，l2+l3≥l1+l4，l4+l3≥l1+l2，l2+l4≥l1+l3整理得g3（X）=x1-1≥0；g4（X）=x2-1≥0；g5（X）=x1+x2-6≥0；g6（X）=-x1+x2+4≥0；g7（X）=x1-x2+4≥0；由图3可知，曲柄存在的杆长之和为无作用约束，起作用的约束条件是机构传动角约束条件g1（X）≥0和g2（X）≥0。同时取机构输出角的平方偏差最小为设计目标：其中输出角，s为φ0～ φ0+90°均匀分布的离散点数，i为各离散点数序号。

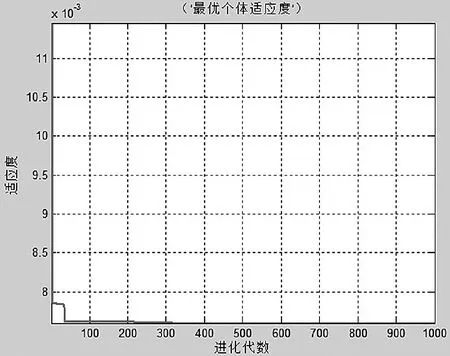
图4 适应度曲线

采用PSO算法求解平面四连杆机构设计问题的最优解，其参数设置如下：粒子群规模设为100，最大迭代次数为1 000，惯性权重为0.729 8，学习因子c1=c2=1.496 18，Vmax=1，Xmax=5，Xmin=1。适应度曲线如图4所示，最终得出函数的全局最优位置为x1=4.131 0，x2=2.319 8；个体最优位置为x1= 4.131 4，x2=2.319 9，函数的最优值为Pbest=0.007 6。

[1]龚松建，袁宇浩，王莉，等.基于PSO优化LS-SVM的短期风速预测[J].可再生能源，2011，29（2）：22-27.

[2]李小为，胡立坤，王琥.速度约束下PSO的六自由度机械臂时间最优轨迹规划[J].智能系统学报，2015（3）：393-398.

[3]Tang Jun，Zhao Xiaojuan.An Enhanced OppositionbasedParticle Swarm Optimization[C].Xiamen，China，2009：149-153.

[4]王凌，刘波.微粒群优化与调度算法[M].北京：清华大学出版社，2008.

2015—10—12