线性规划在政府补贴最小化方面的应用

吉林财经大学 王乔 任俊 杨娅丽

线性规划在政府补贴最小化方面的应用

吉林财经大学 王乔 任俊 杨娅丽

摘 要：“菜篮子工程”是政府为缓解我国副食品供应偏紧的问题而制定的。政府为了促进菜农增加蔬菜的供应量，会采取相应的补贴政策。但是政府的支出预算一般都是有规划的，为了使对蔬菜总的补贴降到最低，本文用线性规划模型来分析一个具体的蔬菜运输案例，分析如何在满足各种外在条件的同时使政府对蔬菜的各种补贴降到最低。

关键词：矩阵算法 产销不平衡 线性规划模型

我国副食品供应偏紧的矛盾已经存在很长一段时间，为了减缓这种供应的矛盾，我国农业部在1988年提出了“菜篮子工程”的方案，并且在相关政策方面，政府也实行了对菜农的蔬菜进行相应的补贴。但是在实际进行补贴时，还会遇到一些具体的问题，比如政府对菜农把蔬菜从种植基地运输到销售点的运输补贴会因为实际路况和运送路线的不同而不同。怎样才能使政府的补贴降到最低，本文用一个简单的案例来解释如何用线性规划解决这个问题。

1 蔬菜运输案例分析及线性规划模型

在A市有8个蔬菜种植基地(A1,A2,…A8)，它们每天的供应量为：40t，45t，30t，38t，29t，35t，25t，28t。每天需要将种植的蔬菜运往市区的35个销售点(1,2,3…35)。当销售点的需求量不能得到满足时，市政府要给予一定的短缺补偿，同时市政府还会按照种植基地供应蔬菜的数量以及路程发放相应的运费补贴0.04元/(1吨.1公里)。

设计出使政府的短缺补偿和运费补贴最少的从种植基地至各销售点的方案，以及各销售点的短缺量一律不超过需求量的30%的方案。

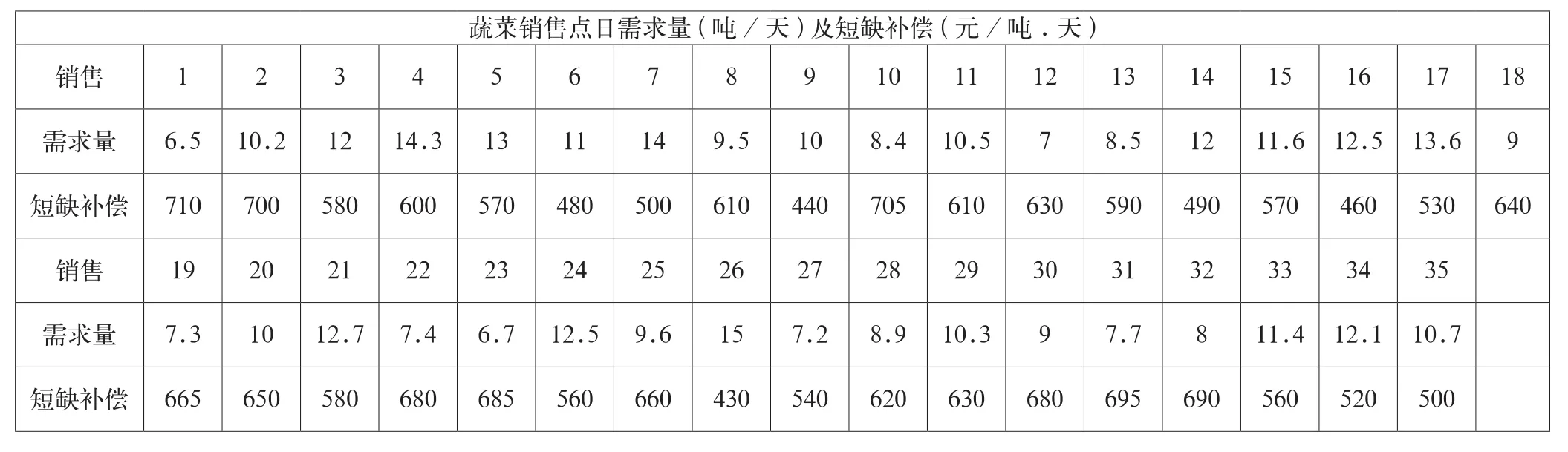
表1 蔬菜销售点日需求量

1.1 使政府的短缺补偿和运费补贴最少的蔬菜运送方案

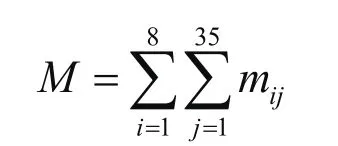
由这一模型可知：将蔬菜从基地i运到销售点j，当运送蔬菜的质量一定时，两点之间的距离越短则这两点之间的政府补贴越少。为了计算各个种植基地和各个销售点的最短距离，将58个点分别编号为A1，A2……A3(种植基地)(销售点)，a1，a2……a15交通路口)，并据此构造的矩阵，用表示第i个点到第j个点的距离，若第i个点和第j个点不相邻，则，根据矩阵并用LINGO求解，如表3所示。

求解得到总费用Z最少为42760.2元，种植基地和销售点之间的具体运输方案如表4。

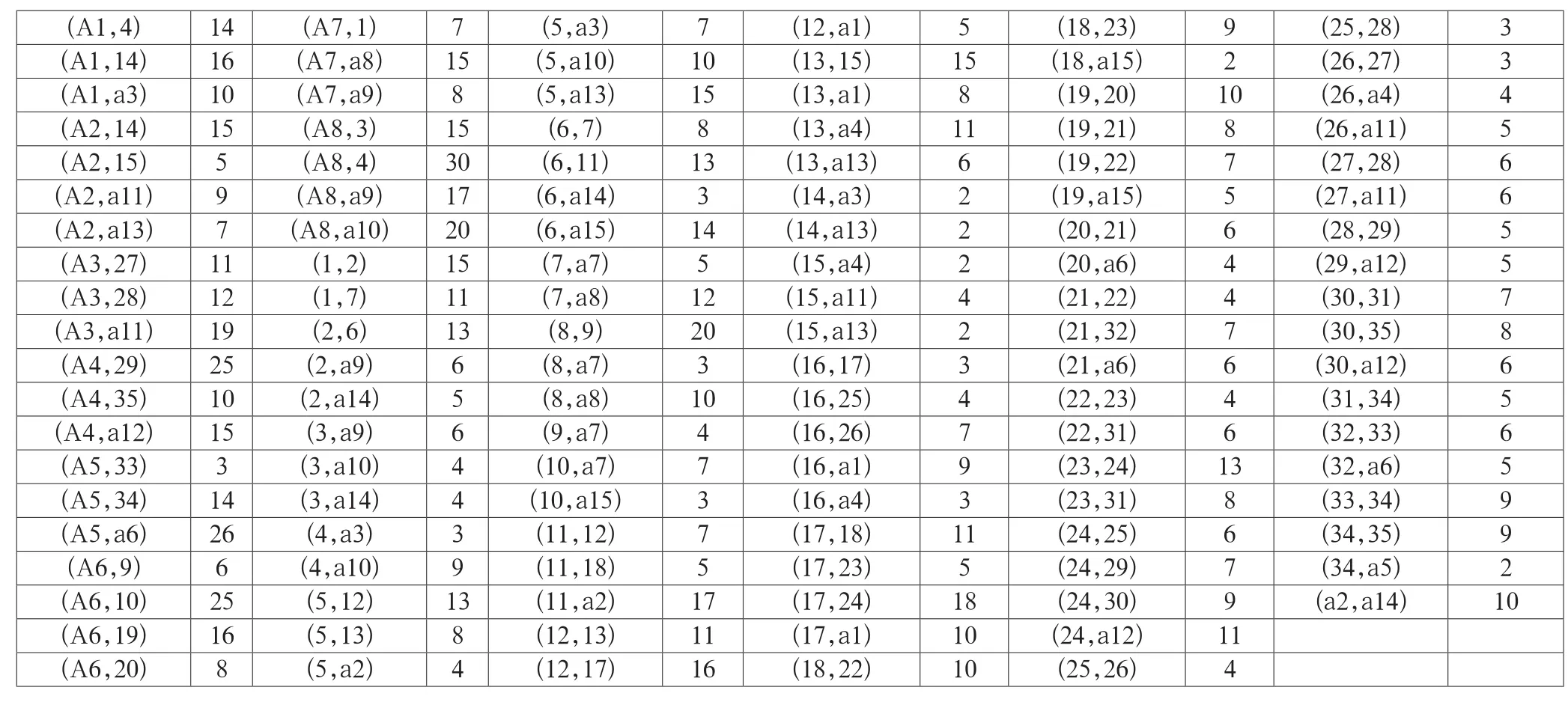
表2 道路交通情况及距离 [基地(A1，A2…A8),销售点(1,2…35),路口(a1,a2…a15)]

表3 种植基地和销售点之间的最短距离

1.2 当各个销售点的短缺量同时满足一律不超过需求量的30%时的运送方案

各个销售点的短缺量都不超过相应需求量的30%，即为各个销售点的总供应量大于其相应需求量的70%，相应的模型为：满足条件为：

根据这一模型并用LINGO解得的使政府短缺补贴和运费补贴最少费用为50407.3元。具体的运输方案为表5：

表4 种植基地和蔬菜销售点之间的运输方案

表5 基地和销售点之间的运输方案

2 结语

菜篮子工程从实施以来惠及了广大居民，但政府的预算支出有限，所以政府要保证惠及居民的同时，尽量节省补贴。本文利用了线性规划模型来解决在满足各种实际状况下使政府总的补贴最少的问题。如果政府面临更加复杂的状况，那么政府可以根据实际情况选择更为有效的线性规划模型来解决问题。

参考文献

[1] 胡运权．运筹学基础及应用(第五版)[M]．北京：高等教育出版社，2012．

[2] 马莉．MATLAB数学实验与建模[M]．北京：清华大学出版社，2010．

[3] 王树祥，武新霞，卜少利．线性规划在企业生产计划中的应用及模型的建立和求解[J]．中国电力教育，2007(S2)．

中图分类号：F812.4

文献标识码：A

文章编号：2096-0298(2015)08(b)-181-03