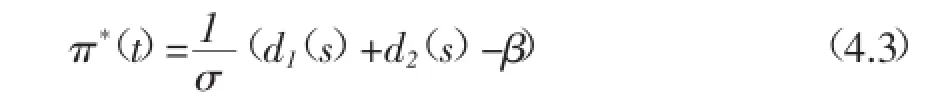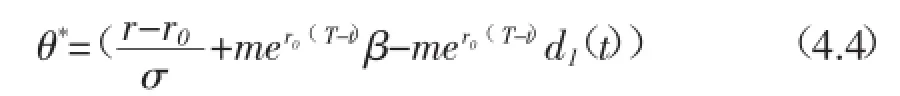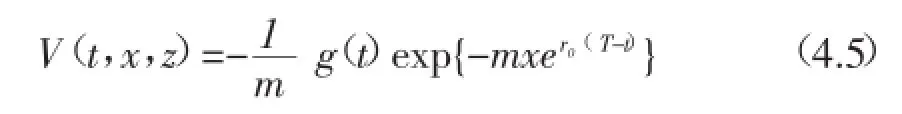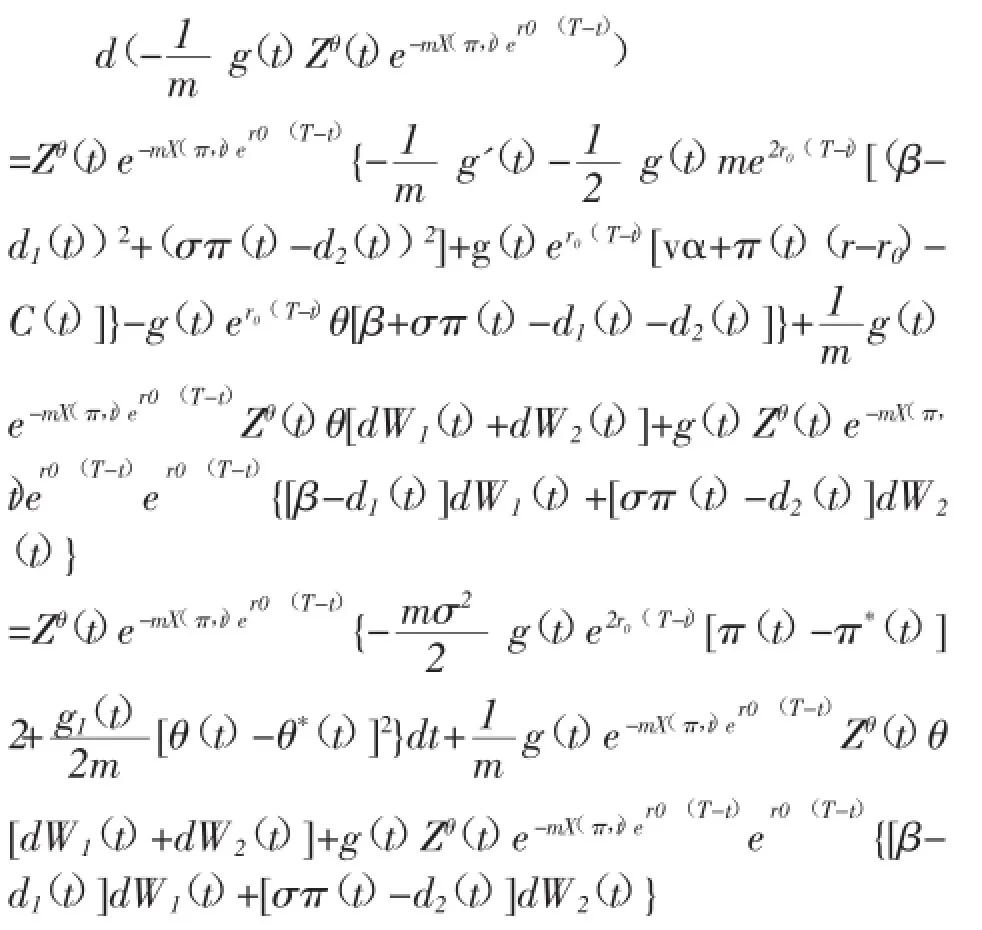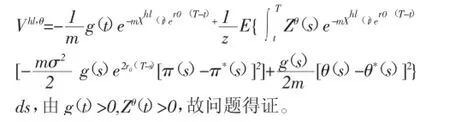基于随机微分博弈的负债型保险公司最优投资策略
王丽霞,李双东
(安徽大学江淮学院,安徽合肥 230601)
基于随机微分博弈的负债型保险公司最优投资策略
王丽霞,李双东
(安徽大学江淮学院,安徽合肥 230601)
在不确定的市场环境下,运用微分博弈理论,建立了带有负债的保险公司与市场的二人零和随机微分博弈风险模型。假定负债过程服从带漂移的布朗运动且与股票价格存在相关性,且保险公司以终值财富期望效用最大化为目标,研究保险公司的投资组合优化问题。应用线性-二次控制方法,在指数效用下,给出保险公司的最优投资策略,市场策略,以及最优策略下终值财富的值函数。
负债;随机微分博弈;线性-二次控制;指数效用
一、引言
现实投资环境下,任何投资个体或投资机构都有可能面临负债,因此研究负债情形下的投资组合问题是风险管理中的重要问题。Xie①Xie S,Li Z,Wang S,“Continuous-time portfolio selection with liability:mean-variance model and stochastic LQ approach”,Insurance:Mathematics and Econom ics,Vol.2,No.3,2008,pp.943-953。研究了负债与股票价格服从不同的布朗运动的情形下均值-方差模型,得到了最优投资策略的显示表达式。荣喜民②常浩,荣喜民:《负债情形下效用投资组合选择的最优控制》,《应用概率统计》2012年第5期,第57-470页。运用随机控制理论通过求解相应的HJB方程给出了负债情形下投资者的最优投资策略的表达式。杨鹏③杨鹏,林祥:《随机微分博弈下的资产负债管理》,《中山大学学报》2013年第6期,第30-33页。研究了负债情形下投资者与市场的随机微分博弈,基于效用最大化原则,求解了最优投资组合策略和市场策略。实际上,多数保险公司也带有负债,李婵娟④李婵娟,李仲飞,曾燕:《带外生负债的保险公司最优再保险——投资策略》,《中山大学学报》(自然科学版)2012年第1期,第1-8页。研究了外生负债影响下保险公司的最优再保险-投资策略,运用随机动态规划方法,得到保险公司分别在能否获取新业务,两种情形下的最优再保险-投资策略以及最优值函数的解析式。张静⑤张静,汪飞星,陈艳萍:《基于风险收益的带负债的再保险——投资策略》,《济南大学学报》(自然科学版)2013年第4期,第15页。则利用变分原理,在一定水平的风险收益下得到保险公司的最优策略以及有效边界。
多数学者对最优投资的研究从投资者的角度出发,而未考虑到市场对投资者的影响。实际上,投资者的决策会随着市场的改变而发生变化。因此,将市场的不确定性因素考虑进来,从投资者和市场两个方面出发,所得模型将更符合实际,这就将问题转化成了随机微分博弈。近年来,很多学者对此作了研究。Browne⑥Browne S,“Stochastic differential portfolio games”,JAppl Probab.Vol.37,No.1,2000,pp.126-147.利用随机微分博弈方法研究了最优投资问题,Korn⑦Korn R,Steffensen M,“On worst-case portfolio optimization”,SIAMJ Control Optim,Vol.46,No.6,2007, pp.2013-2030.研究了微分博弈中"最坏情形"下的组合优化问题,即投资者选择投资组合和他的对手,市场选择最坏情形。Elliott⑧Elliott RJ,Siu TK,“Robust optimal portfolio choice under Markovian Regime-switching Model”,Methodol Comput Appl Probab,No.11,2009,pp.145-157.研究了连续时间马尔科夫市场中的最优投资组合选择问题,在投资者面临不确定性情形下寻求最优投资组合策略。随着微分博弈思想在金融领域发挥的作用越来越大,一些学者开始将该思想运用到保险领域,Korn①Korn R,“Worst-case scenario investment for insurers”,Insur Math Econom,No.36,2005,pp.1-11在保险公司面临市场最坏情形下,建立扩散型风险,研究模型组合优化问题。Zhang②Zhang X,Siu TK,“Optimal investment and reinsurance of an insurer with model uncertainty”,Insur Math Econ,No.45,2009,pp.81-88.基于随机微分博弈思想探讨最优投资及再保险保险策略。Taksar③Taksar M,Zeng XD,“Optimal non-proportional reinsurance control and stochastic differential games”,Insur Math Econ,No.48,2011,pp.64-71.在保险公司以非比例再保险形式分保的情况下建立复合泊松风险模型的扩散逼近模型。Lin④Lin X,Zhang C,Siu T K,“Stochastic differential portfolio games for an insurer in a jump-diffusion risk process”,Mathematical Methods ofOperations Research,Vol.75,No.1,2012,pp.83-100.运用线性二次控制方法基于微分博弈思想研究了跳扩散风险模型及其扩散逼近下保险公司的投资组合策略。
以上文献在运用微分博弈思想研究研究保险公司的投资策略的同时,并未考虑保险公司的负债,负债作为大多数金融机构面临的实际情况,对保险公司的投资决策起着重要的影响。因此,本文在Lin⑤同④。的基础上考虑保险公司带有负债,建立在负债情形下,保险公司与市场之间二人零和随机微分博弈问题,以最大化终值财富期望效用为准则,利用线性二次控制方法,在指数效用下分析保险公司的最优投资策略,和作为保险博弈的对手的市场的策略。
二、模型建立
假设保险公司的平均索赔及索赔波动率分别为α,β,满足α>0,β>0且均为常数,常数v(>0)为保险公司的安全负载,故盈余过程满足如下微分方程

假设投资者初始时刻t=0的财富为w(w>0),负债为l(l∈R),则投资者在初始时刻的财富净值x0=w-l>0。记L(t)为到达t时刻的累计负债,满足

其中c(t),d1(t),d2(t)均为t的确定函数,d1(t)表示由于保险公司保费及索赔的不确定性引起的负债波动率,d2(t)表示由于风险资产价格的波动引起的负债波动率。
假设保险公司将自己的资产进行投资,且在金融市场中有两种金融资产:
(1)无风险资产(银行账户),其价格演化方程为

其中r0>0表示无风险利率;
(2)风险资产,其价格演化方程为
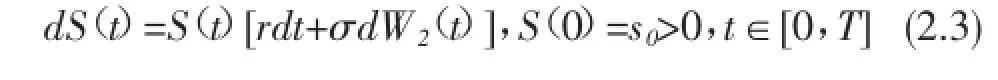
上式中r>r0,σ>0为常数。
设在t时刻保险公司投资于风险资产的投资额为π(t),则无风险资产的投资金额为X(π,t)-π(t),其中X(π,t)为投资策略为π(t)下的盈余过程,结合(2.2)及(2.3)式,盈余过程X(h,t)满足如下随机微分方程
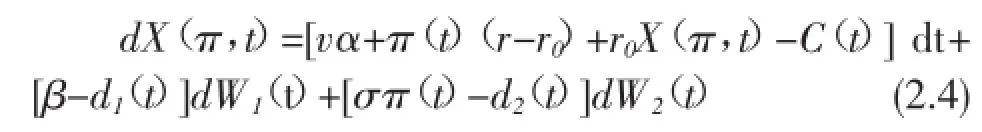
定义:若π(t)是Ft自适应的,对每个t∈[0,T]满足,且随机微分方程(2.4)对策略π有唯一强解,则称之为可行策略。
记所有可行策略的集合为Π。
三、问题形成
本文假设保险公司以最大化终值财富期望效用为经营目标,而市场通过选择适当的概率测度最小化终值财富期望效用,以下引入市场控制的概率测度集,假设Ft可测的随机过程{θ(t),t∈(0,T)}满足,记满足上述条件的θ(t)的全体集合为,对于每个θ(t),t∈(0,T),定义{Zθ(t),t∈(0,T)}如下
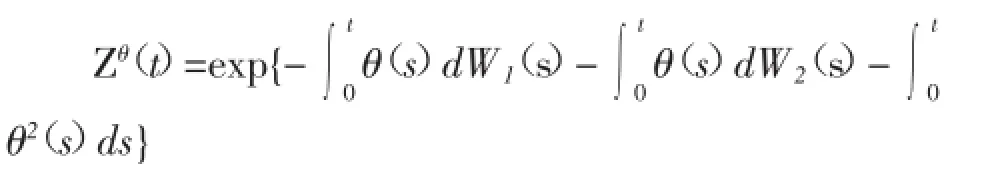
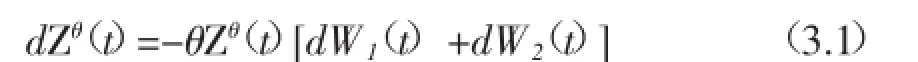
假设{θ(t),t∈(0,T)}几乎处处有界,Zθ(0)=Z0(0 假设u:R→R为一个效用函数,满足u'>0,u"< 0(u是一个严格凸函数)。对每个策略π(t),定义保险公司的终值财富在Pθ下的期望效用函数为 其中Eθ是概率测度Pθ下的数学期望。 保险公司的策略选择依赖于市场,即市场为博弈的主导者,则保险公司的目标是在市场最坏的情形选择一个最优策略π(t),最大化终值财富效用,即 这是保险公司与市场之间的二人零和随机微分博弈问题,其中π*(t)为保险公司的最优投资,θ*为最优市场策略。解决该问题即要找到最优策略(π*,θ*)∈Π×Θ和对应的值函数V(t,x,z)。 本文在指数效用下讨论随机微分博弈问题(3.2)的最优解和值函数。 引理1 g(t)满足如下常微分方程 证解常微分方程(4.1)即可得结论。 定理1在指数效用下,随机微分博弈问题(3.2)的最优投资策略为 市场的最优策略为 对应的值函数满足 其中g(t)满足(4.2)式。 证令π(·)和θ(·)为一组可行策略,X(π,t)满足(2.4)式,对应用公式,结合(4.2)式 其中π*,θ*分别满足(4.3)及(4.4)式,对上式从t到T积分,并在条件X(π,t)=x,Zθ(t)=z及概率测度Pθ下,取条件期望,得 注1定理1表明保险公司的负债会影响保险公司的最优策略及市场策略,最优投资策略随着负债波动率d1(t)及d2(t)的增大而增大,随着索赔波动率β的增大而减小,且当d1(t)+d2(t)<β时,保险公司必须卖空所有资产还对承保风险。最优市场策略随着由保险公司保费及索赔的不确定性引起的负债波动率d1(t)的增大而减小,需要注意的是,影响最优策略的并不是负债数额,而是负债的波动率。 注2当c(t)=d1(t)=d2(t)=0时,即若不考虑负债存在的情形,结论与文①Lin X,Zhang C,Siu T K,“Stochastic differential portfolio games for an insurer in a jump-diffusion risk process”,Mathematical Methods of Operations Research,Vol.75,No.1,2012,pp.83-100.所得结论一致。 Optimal investment strategy for an insurer with liability based on stochastic differential games WANG Lixia,LI Shuangdong In the uncertain market environment,a two-person,zero-sum,stochastic differential game risk model between market and an insurer who faces liability is established by using a differential game theory.In the model,the insurer's portfolio optim ization problem is studied,assum ing that the liability process follows Brownian motion with drift and is comp letely correlated with stock prices,and the aim of the insurer is to maxim ize the expected utility of term inal wealth.With the exponential utility function,the insurer's optimal investment strategies,the best marketing strategies and the value function of terminal wealth under the best strategies are obtained by app lying linear-quadratic controlmethod. liability;Stochastic DifferentialGames;linear-quadratic control;exponentialutility O225 F840.32 A 1009-9530(2015)05-0023-03 2015-08-12 安徽大学江淮学院院级基金资助“带投资的再保险模型的随机微分博弈问题研究”(2014KJ0001);安徽省质量工程项目资助“基于数学建模思想的独立学院学科竞赛体系的研究”(2013jyxm525) 王丽霞(1984-),女,安徽大学江淮学院讲师,概率论与数理统计专业硕士。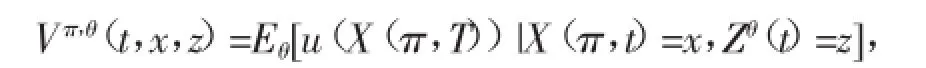
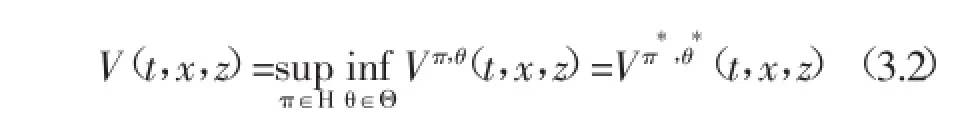
四、最优策略与值函数