失效数据的威布尔分布建模与参数估计方法

顾国梁，王景芹

（河北工业大学电气工程学院，天津 300130）

失效数据的威布尔分布建模与参数估计方法

顾国梁，王景芹

（河北工业大学电气工程学院，天津 300130）

低压电器产品的可靠性与生产生活密切相关，因而对产品进行可靠性评估显得十分重要，分析产品的失效数据是可靠性评估的重要手段．威布尔分布是一种常见的产品寿命分布，低压电器产品的失效数据服从不同参数的威布尔分布．本文研究了基于威布尔分布的失效数据的数据处理过程．首先研究了威布尔分布的图检验法，并用最小二乘法计算拟合直线方程和线性相关度．然后用F检验法对失效数据是否符合威布尔分布进行了验证．对于确定符合威布尔分布的失效数据，本文采用极大似然估计法计算威布尔分布参数的点估计值并由此计算参数和可靠性特征量的区间估计．最后，通过具体算例对一组接触器失效数据进行威布尔分布建模并计算相关参数．关键词威布尔分布；数据处理；极大似然估计；点估计；区间估计

0 引言

低压电器通常是指在低压配电系统与控制系统中起开关、控制、保护、检测、显示和报警等作用的元件或装置[1]，其可靠性水平对生产及日常生活的影响巨大，因而对产品进行可靠性评估显得十分重要．文献[2-3]分别对电力系统和继电保护可靠性评估方法进行了相关报道，而对低压电器产品的失效数据进行威布尔分布建模，进而估计其可靠性特征量的可靠性评估方法还未见报道．

众所周知，绝大部分产品的寿命过程都经历3个阶段：早期失效阶段、偶然失效阶段和耗损失效阶段．分析的失效数据是经过可靠性筛选试验剔除了早期失效产品后得到的，文献[4]对小型断路器可靠性筛选的方法进行了报道．威布尔分布是可靠性理论中常用的最复杂的一种分布，大量工程实践表明，低压电器产品的失效数据服从不同参数的威布尔分布．因此，验证产品的失效数据符合威布尔分布并计算出威布尔分布参数就显得尤为重要．对低压电器产品的失效数据进行分析和对失效规律的研究是电器可靠性研究方向的重要课题．

在IEC 60947-4-1（低压开关设备和控制设备第4-1部分接触器和电动机启动器机电式接触器和电动机启动器）的附录K[5]中给出了确定在功能安全性应用中所用的机电式接触器可靠性数据的步骤，但其数据处理过程过于简略，也未给出威布尔分布参数的数值计算方法和产品可靠度的估计方法．本文对数据的威布尔拟合和参数估计做了细致的研究．在研究过程中，通过大量的验证与查阅资料，修正了一些文献中不正确的公式，给出了恰当的数据处理过程．对于小样本及无失效数据时电器产品可靠性特征量的估计可参考文献[6]．

1 威布尔分布的检验方法

1.1 威布尔分布

1.1.1 威布尔分布的定义及3个参数

若随机变量L的密度函数即失效密度函数为

1.2 威布尔分布的检验方法

对于实际收集到的失效数据，为证实其失效分布类型为威布尔分布．目前常用的检验方法有图检验法和数学方法，即统计分析的方法（如2检验法，K-S检验法等）进行非参数假设检验．

1.2.1 威布尔分布的图检验法

图检验法与统计分析的方法相比具有简单易行、使用方便、直观易懂、容易掌握的特点，可以直观的对失效数据是否符合威布尔分布进行检验．但作图法准确度较差，所得的结果往往因人而异，甚至有时难以得到一个确切的结论．

下面用统计学方法即曲线拟合的最小二乘法对参数进行估计．

根据威布尔分布的特点及威布尔概率纸的原理可知，对于不同的失效时刻ti有

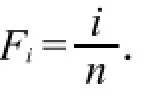
|r|=1时，所有点都在回归直线上，此时称x与y完全线性相关，但实际失效数据很少见到这种情形．

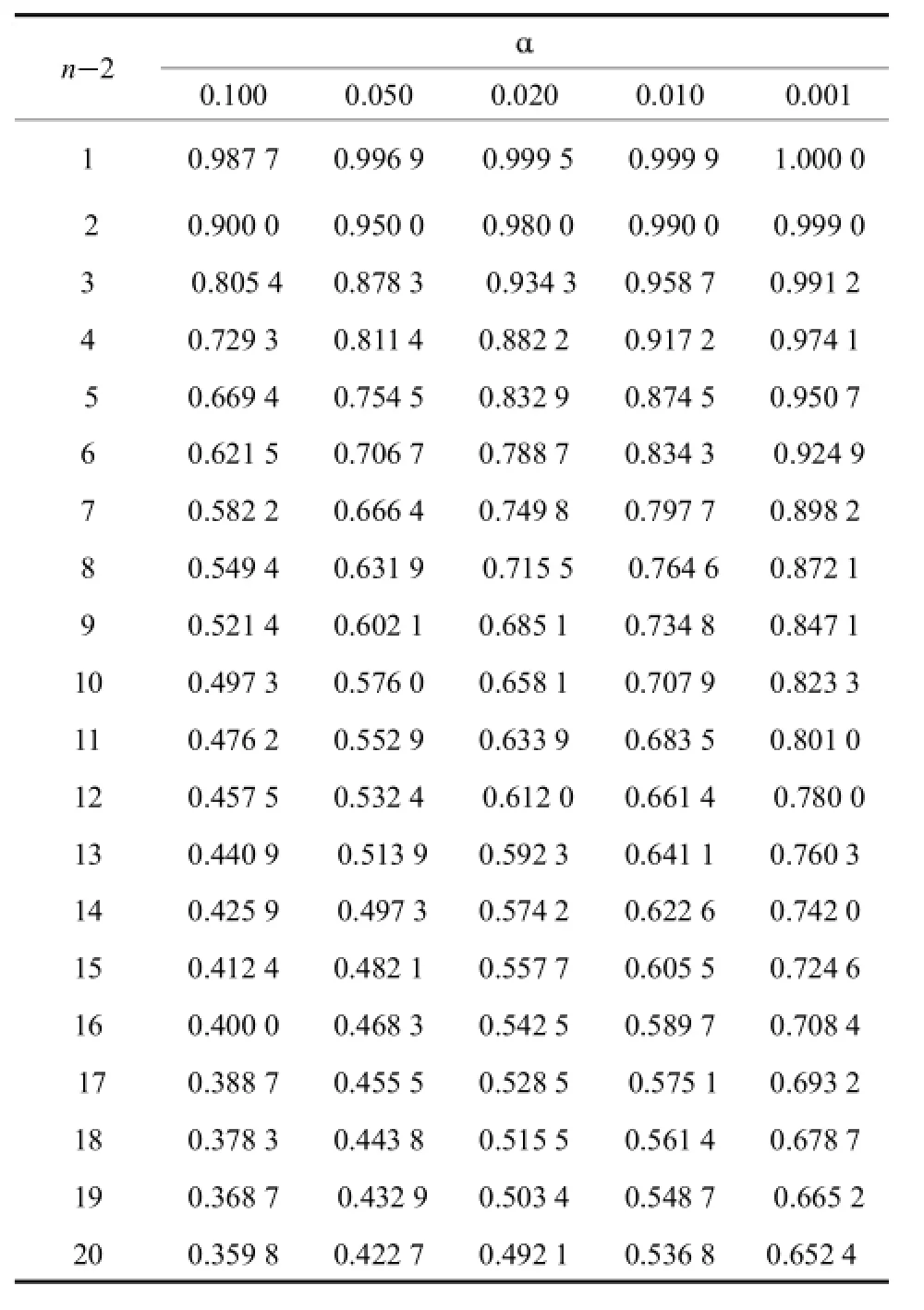
表1 相关系数临界值表（p r＞r=）Tab.1The critical value of the correlation coefficient

对r的检验的临界值可通过查表1得到．当r＞r时，可认为回归效果显著，即可以接受曲线拟合后的回归直线方程；当r＜r时，认为x与y的相关性较差，不能接受曲线拟合后的回归直线方程．表中n 2是自由度，n为失效数据的个数．

1.2.2 威布尔分布的统计检验方法

作图法验证失效数据符合威布尔分布的方法可能会因为人为因素造成作图误差，导致判断不精确．因此，用数理统计的方法验证失效数据满足威布尔分布显得尤为重要．常用的方法有皮尔逊2检验、柯尔莫哥洛夫-斯米尔诺夫检验（K-S检验）以及对威布尔分布的F检验法．但由于x2检验法和K-S检验法需要预先对理论分布函数的参数进行估计，对于威布尔分布的检验较为不利，因而本文采用F检验法来检验．过程如下：

对于定时截尾寿命试验，设截尾时间为t0，将故障时间从小到大排列，则r个故障时间为0＜t1t2t3…trt0，设xi=lnti，建立假设则拒绝原假设，该批数据不是来自威布尔分布的总体，反之则接受．

此方法适用于定时截尾和定数截尾试验数据．其优点是计算时不用查找特殊的专用表格，只使用普通常见的F分布表，列表计算也较为方便．

2 威布尔分布可靠性特征量的估计

2.1 威布尔分布参数的点估计值

在威布尔分布的图检验法中，介绍了参数的最小二乘估计法，用于计算点估计值．文献[12]利用威布尔分布的均值和方差计算参数的估计值．下面本文介绍用极大似然估计法计算威布尔分布的参数．

将式(3)代入式(2)得

式中：ti代表每个参加试验产品的试验时间，n为试验样品数，r为失效数．另外，此方法求出的m的极大似然估计值存在且唯一[14]．

2.2 威布尔分布参数的区间估计

当用极大似然估计法计算威布尔分布参数的点估计值时，本文采用下面的方法计算威布尔分布参数的区间估计．它适用于完全样本及定数、定时试验子样．设有n个试样进行试验，试验截止时间为tr，共有r个产品故障，故障时间为t1t2t3…tr．设由极大似然估计法得到的参数点估计值为m^和^．

2.2.1 参数m的区间估计

式中：A1、A2为系数，其计算分为完全样本（n=r）和截尾样本（r＜n）两种情况．首先计算以下常数

2.3 可靠性特征量的区间估计

2.3.1 可靠寿命tR的估计

对可靠度为R时的可靠寿命，在参数点估计已知时，由式(6)得其点估计

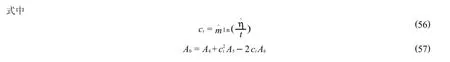
2.3.3 失效率的估计

由式(5)和式(3)可以得到

本文中给出的部分计算公式是通过数值计算后，用拟合法得到的，其误差一般在1%～2%以下，满足工程计算要求．

3 算例

采用具体算例研究对1组失效数据进行威布尔分布类型的检验及相关可靠性特征量的估计．总共有15台接触器（n=15）同时进行试验直到全部失效．其失效时间（r=15）见表2．

3.1 威布尔分布的图检验法

首先检验表2中的数据是否满足威布尔分布，由公式(10)计算F ti计算结果如表2．在威布尔概率纸上，按（ti,F ti）描点，其轨迹如图1所示．

从图1中可以看出，其轨迹近似为一条直线，可以认为接触器的失效数据服从威布尔分布．从软件分析结果可以看出，形状参数和真尺度参数的值分别为m=4.347，=2149130．

取可靠度R=0.9，则F=1 R=0.1，在威布尔概率纸（图1）F t尺上找到F ti=0.1的点向右作水平线与回归直线相交，再由交点向下作垂线，此垂线与t尺交点的读数即为可靠度为0.9时的可靠寿命t0.9的估计值即=1 265 000（次），由=63.38得到拟合曲线方程为

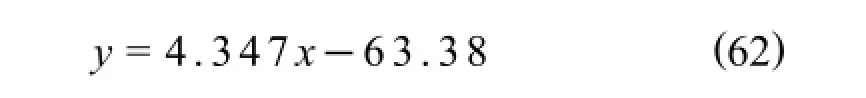
至此，根据在威布尔概率纸上得到的（ti,F ti）的轨迹为一条直线，证明失效数据服从威布尔分布．然后，得到了威布尔分布的形状参数和真尺度参数m，的估计值，并计算出拟合后的曲线方程(62)．下面，通过统计学中的最小二乘法计算拟合曲线方程，并通过相关系数r检验直线的线性相关程度．

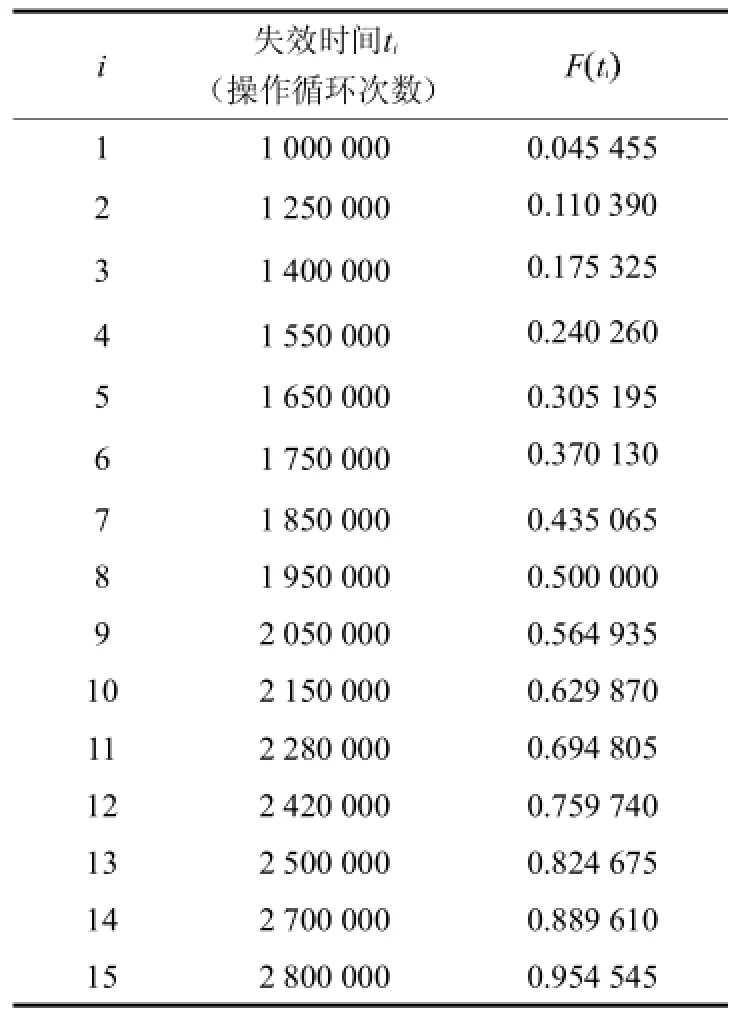
表2 F ti的计算结果Tab.2The value of F (ti)

3.2最小二乘法曲线拟合

将失效数据代入式(9)、式(10)，计算xi，yi．由式(12)、式(13)计算．结果为=3.908，=57，r=0.998 8．

根据计算结果由式(11)得到曲线拟合的线性回归方程为

由计算结果得到r=0.998 8＞r=0.513 9，可以认为线性回归效果显著．

比较式(62)、式(63)可以看出，用最小二乘法得到的拟合曲线方程与图估计法得到的结果接近，但存在一定的偏差，这是由于软件绘图计算的结果是基于直线的整体走向确定的，会忽略偏离直线较远的点．而最小二乘法是基于所有失效数据确定的，由于偶然因素导致个别数据偏离直线较大，其对参数的计算会产生影响．因此，通过软件绘图从直线整体走向计算的结果相对最小二乘法更精确．在计算精度要求不高的条件下，两种方法得到的计算结果都可以用来估计可靠性特征量，同时，两者也都可以说明失效数据近似为威布尔分布．

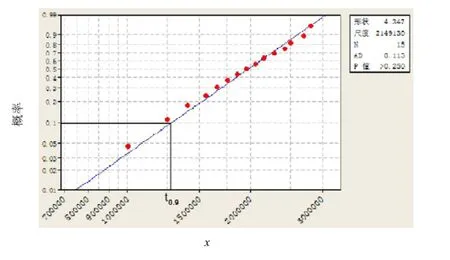
图1 威布尔分布中位秩回归直线Fig.1Plot of Weibull median rank regression

3.3 失效分布类型的统计学检验法（F检验法）由1.2.2节所述，在验证失效数据符合威布尔分布时，通常采用F检验法进行验证，过程如下：将失效数据代入式(22)～式(23)，其中r=15，计算结果如下

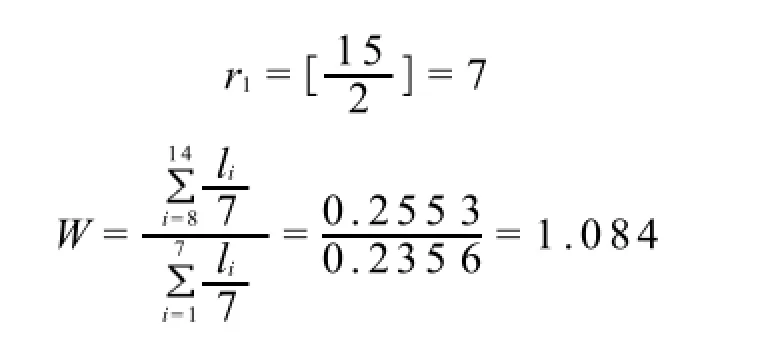
3.4 分布参数的确定

对于已经证实符合威布尔分布的失效数据，要进行威布尔分布参数的确定．首先，由极大似然估计法（MLE）计算参数的点估计值．对于算例中的失效数据，n=r，则式(28)可表达为式(64)

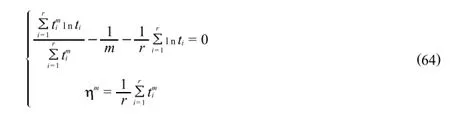
本文采用二分法求解参数m，令

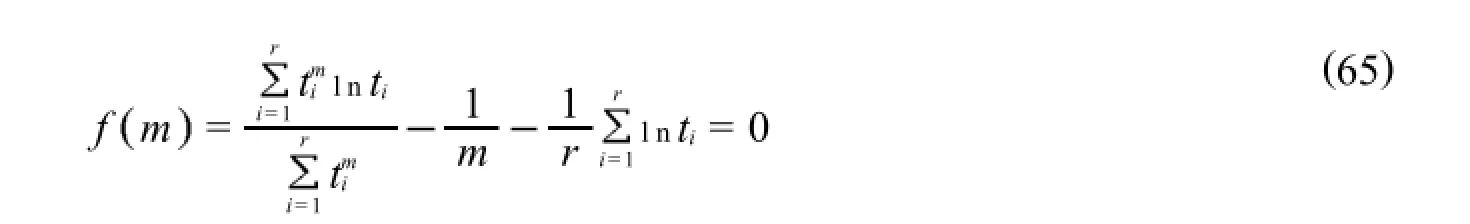
3.5.4 可靠度的估计

对于实际产品使用过程中任意时刻的可靠度，其点估计值可将时刻t代入式(54)求得Q1=0.866，时刻t的可靠度下限可由式(55)求出．

3.5.5 失效率的估计

4 结论

本文对基于威布尔分布的失效数据的检验方法以及威布尔分布参数和可靠性特征量的点估计和区间估计进行了全面细致的研究，提出了对失效数据进行处理的具体方法，为日后进一步的可靠性研究奠定了基础．

参考文献：

[1]陆俭国，李奎，杜太行，等．塑壳断路器可靠性理论与验证试验方法[J]．电工技术学报，2012，27（5）：180-185．

[2]孙羽，王秀丽，王建学，等．电力系统短期可靠性评估综述[J]．电力系统保护与控制，2011，39（8）：143-154．

[3]戴志辉，王增平．继电保护可靠性研究综述[J]．电力系统保护与控制，2010，38（15）：161-167．

[4]骆燕燕，陆俭国，李志刚．小型断路器可靠性筛选方法的研究[J]．电工技术学报，2003，18（2）：36-40．

[5]IEC 60947-4-1，Annex K Procedure to determine data for electromechanical contactors used in functional safety applications[Z]．

[6]王景芹，唐义良，陆俭国．小样本及无失效数据时电器产品可靠性特征量的估计[J]．电工技术学报，2000，15（4）：27-31．

[7]陆俭国，王景芹．低压保护电器可靠性理论及其应用[M]．北京：机械工业出版社，2004：34-38．

[8]陆俭国．电器可靠性理论及应用[M]．北京：机械工业出版社，1996：53-56．

[9]戴志辉，王增平，焦延军等．基于缺陷分析的保护装置可靠性评价研究[J]．电力系统保护与控制，2013，41（12）：54-59．

[10]刘达民，程岩．应用统计[M]．北京：化学工业出版社，2004：86-89．

[11]贺国芳．可靠性数据的收集与分析[M]．北京：国防工业出版社，1995：167-168．

[12]张钊，陈金木，陈昊．一种基于可用率约束的电气设备计划维护优化模型[J]．电力系统保护与控制，2011，39（23）：85-88．

[13]李庆阳，王能超，易大义．数值分析[M]．北京：清华大学出版社，2008：212-214．

[14]曹晋华，程侃．可靠性数学引论修订版[M]．北京：高等教育出版社，2006：407-409．

[15]赵宇．可靠性数据分析[M]．北京：国防工业出版社，2011：161-162．

[16]崔立荣．两参数威布尔分布的统计方法[J]．质量与可靠性，1992，2：30-33．

[17]盘吉安．可靠性维修性可用性评估手册[M]．北京：国防工业出版社，1995：190-191．

[责任编辑 代俊秋]

Weibull modelling and parameter estimation method of failure data

GU Guoliang，WANG Jingqin

(School of Electrical Engineering,HeBei University of Technology,Tianjin 300130,China)

The reliability evaluation of is very important since low voltage electrical appliances are closely related to the production andliving.Analysing thefailure data isa goodaccess tothat.Weibulldistributionisa common lifedistribution，the failure data of low voltage electrical appliances conform to Weibull distribution,but they have different parameters. In this paper,we do research on data processing of failure data which is based on Weibull distribution.Firstly we study the figure testmethod of Weibulldistribution and use theleast square method to calculate thefittinglineequation and linear correlation.Secondly,we use F test method to verify that the failure data conform to the Weibull distribution.If the failure data fit for Weibull distribution.We use maximum likelihood estimation(MLE)to calculate the point estimation of Weibull parameters and we use it to calculate the interval estimation of the Weibull parameters and reliability characteristics.At last,we use the failure data of contactors to do the Weibull modelling and calculate the related parameters.

weibulldistribution;dataprocessing;maximumlikelihoodestimation(MLE);pointestimate;intervalestimate

TM930

A

1007-2373(2015)03-0007-10

10.14081/j.cnki.hgdxb.2015.03.002

2015-01-13

国家自然科学基金（51077039）；河北省自然科学基金（E2012202111）；河北省“百千万人才工程”人才培养资助项目（A2013007001）作者简介：顾国梁（1990-），男（汉族），硕士生．通讯作者：王景芹（1964-），女（汉族），教授，博士生导师．

数字出版日期：2015-06-16数字出版网址：http://www.cnki.net/kcms/detail/13.1208.T.20150616.0928.004.html