FMEA方法改进及其在技术创新风险管理中的应用
罗小芳, 李柏洲, 白 旭
FMEA方法改进及其在技术创新风险管理中的应用
罗小芳1, 李柏洲2, 白 旭3
(1.江苏科技大学 经济管理学院,江苏 镇江 212003; 2.哈尔滨工程大学 经济管理学院,黑龙江 哈尔滨 150001; 3.江苏科技大学 船舶与海洋工程学院,江苏 镇江 212003)
在资源有限的情况下,企业技术创新风险管理的关键是主要风险的识别和防范。首先,基于合理的猜想,从优化结果角度,提出了基于可靠指标矢量-概率网格估算法的改进的FMEA方法,即在传统FMEA方法基础上,基于失效模式相关性进行失效模式替代,得出技术创新过程中的主要失效模式。其次,将改进的FMEA方法应用于一个技术创新风险管理案例,并与传统方法进行比较分析,分析结果表明:改进的FMEA方法用于风险管理不仅能节省企业资源,还能提高企业技术创新风险管理效率,是企业有效的技术创新风险管理定量分析工具。
创新风险管理;FMEA;可靠指标矢量;概率网格法;
0 引言
随着全球知识经济时代的到来,技术创新成为企业生存、发展及在行业中处于不败之地的关键,然而,创新与风险是一个不可分割的统一体[1],技术创新风险管理效率决定了企业创新的成功率。目前已有技术创新风险管理的研究均为定性分析[2,3],其中一个重要原因是缺乏有效的技术创新风险管理定量分析工具。探寻有效的技术创新风险管理定量分析工具,提高企业创新风险管理效率能有效促进企业技术创新的开展与成功。
FMEA(Failure Modes and Effects Analysis,失效模式与影响分析)起源于20世纪60年代中期美国的航空工业公司[4],是一种系统化的工作技术和模式化的思考形式[5]。它考虑产品或服务可能的失效,再确定其频率和影响过程,既可用于风险的事前预防,也可用于其事后改进[6],现已被成功应用于航空航天、机械、汽车及医疗设备等领域的产品、工艺设计失效模式及其效果的分析。针对FMEA存在的缺陷[7~9],已有学者进行了大量改进方面的研究:Keller等人研究了利用模糊逻辑规则来表述各种原因和影响效果之间的相互作用[10]。Bell建立了FMEA的原因推理模型,以FMEA语言方式进行推理表达[11]。Bowles和Pelaez研究了在关键因素分析中利用关系方程进行推理和非模糊化的方法[12]。Chang和Pillay等人将灰色关联决策应用到FMEA的研究框架中[13-14]。Antonio等人将模糊推理系统的方法应用于FMEA中[15]。以上改进均是从优化FMEA分析过程的角度进行的,主要是将模糊集理论和灰色理论应用于FMEA分析过程。
本文运用FMEA方法分析企业技术创新过程中的失效模式及其影响,提供一种企业技术创新风险管理的定量分析工具。鉴于企业用于创新的资源是有限的,不可能花费过多资源和精力用于创新风险的防范与管理,而只能对其中最主要的、发生概率较大的风险进行处理,主要失效模式识别成为企业技术创新风险管理的关键。技术创新风险管理中风险因素、失效模式众多,同时风险因素及失效模式间还存在很强的相关性[1,16],若直接利用FMEA方法分析得出的所有模式中,若干模式间的相关性达到某一标准,则可用其中发生概率最大的模式来代替其它几个模式,对其中发生概率最大失效模式的防范也就意味着同时已对与其相关性较强失效模式进行了处理,能有效避免重复处理,节省企业资源,同时也能将剩余资源用于其它失效模式的防范,提高企业技术创新风险管理效率。因此,基于这一猜想,从优化FMEA分析结果的角度,本文提出了基于可靠指标矢量及概率网格估算法的FMEA方法改进,与传统方法的案例比较分析表明:本文改进的FMEA方法能有效发掘企业技术创新过程中需处理的主要失效模式,既能节约企业资源,又能提高企业技术创新风险管理效率。
1 传统FMEA方法
运用传统FMEA方法进行技术创新风险分析的主要步骤包括[6]:
第一,对创新过程进行任务分解,并得出每一任务中可能产生的失效模式及其风险因素。
第二,确定各种失效模式发生的严重度(S)、频率(O)和可检测概率(D)。
第三,依据S、O、D计算失效模式的风险顺序数(Risk Priority Number,RPN)。
第四,根据最低可接受原则(As Low As Reasonably Practicable,ALARP),判定各种风险是否可接受,若判定结果为可接受,则根据企业实际情况,针对分析结果进行相应的风险管理即可。若判定结果为不可接受,说明该技术创新方案不可行,必须对方案进行方法改进或者采取相应的预防措施后,使风险降至可接受范围后才可施行。
其中,第一、第二步由企业技术创新负责人组织相关人员通过讨论确定,第三步可通过RELEX软件计算得出,第四步由技术创新相关专家根据经验设定可行的RPN范围进行判定,并制定相关政策措施。
2 改进的FMEA方法
2.1 改进的FMEA方法流程分析
本文对FMEA方法的改进是在传统FMEA方法第三步之后,加入失效模式相关性计算及失效模式排序与替代两个步骤。改进后FMEA方法流程如图1。
第一步,通过传统FMEA方法的前三步计算得出RPN值。
第二步,失效模式相关性计算。设失效模式发生的概率为pi(i=1,2,…,n),失效模式影响因素有xk(k=1,2,…,m),xk对pi影响程度为ak(0≤ak≤1)。则pi=akxk。通过将pi转化为矢量,并根据可靠指标矢量相关性的计算可得出ρij(j=1,2,…,n,j>i)。同时,设定ρ0(0<ρ0<1)为判断各失效模式相关程度的依据。若ρ0取值较接近1,失效模式替代原则较严格,技术创新风险管理偏保守;反之,若ρ0取值较接近0,技术创新风险管理偏激进。ρ0的确定应根据企业实际情况做出,可通过计算风险管理过程中的成本-收益率来选择严格或者宽松的风险管理政策,选择使企业达到收益最大化的ρ0值。pi、xk、ak、ρ0均需由技术创新专家确定。
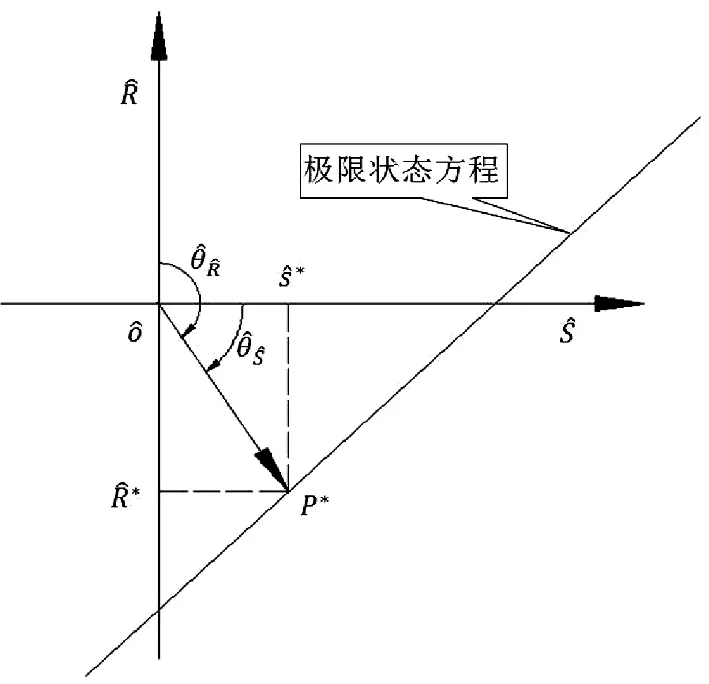
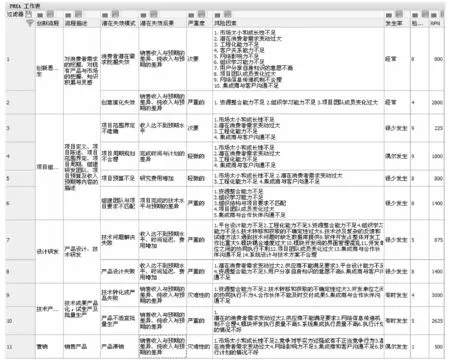
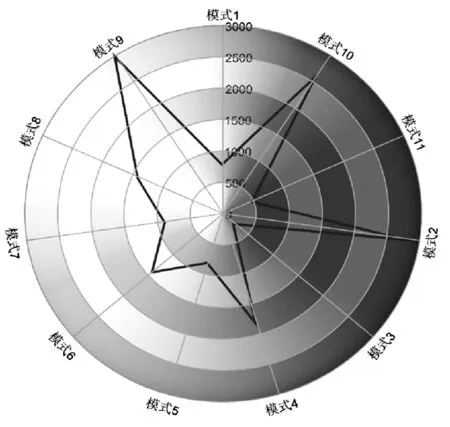
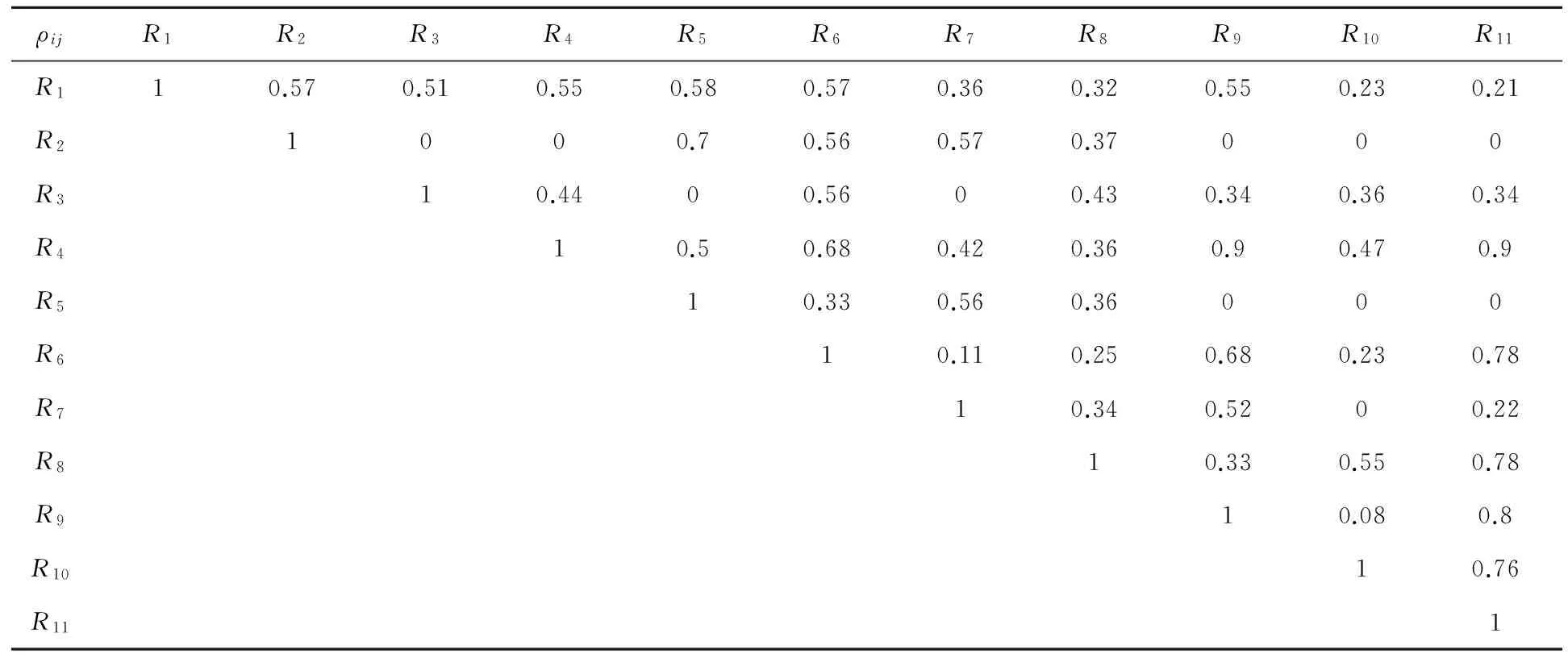
第三步,失效模式的排序与替代。具体过程为:首先,根据第一步中RPN值从大到小的顺序对失效模式Mi(i=1,2,…,n)进行排序,并以Ri(i=1,2,…,n)编号。然后,取R1(R1=max{RPN(Mi)}),R1与R2的相关系数为ρ12。若ρ12≥ρ0,就认为R2可被R1替代;若ρ12<ρ0,则保留R2,Ri与Rj(i 第四步,同传统FMEA方法中的第四步。 改进FMEA方法中,失效模式间的相关系数基于可靠指标矢量计算得出,失效模式的排序与替代采用概率网格估算方法进行,其最终目的是获得技术创新过程中的主要失效模式。第二步的关键是基于可靠指标矢量计算失效模式间的相关系数,第三步的关键是运用概率网格法进行失效模式的替代。 图1 改进的FMEA方法流程图注:图1中两个粗线框表示对传统FMEA方法进行了改进的环节 2.2 基于可靠指标矢量的失效模式相关性计算 2.2.1 可靠指标矢量 可靠指标(Reliability Index,RI)是度量结构可靠度的一种数量指标,为结构功能函数的均值与标准差的比值,与结构的失效概率在数值上有对应关系[17]。在本文的分析中,借鉴结构分析中这一概念,设可靠指标β与失效模式发生的概率ρ相对应。 假设存在两个随机变量R和S,设两个随机变量的极限状态方程可表示为: z=g(R,S)=R-S=0 (1) 式(1)中R和S相互独立并服从正态分布,均值分别为μR和μS,标准差分别为σR和σS。对R和S做标准正态转换,(1)式可以表示为: (2) 图2 极限状态方程曲线 则: (3) 根据矢量运算法则,有: (4) (5) β是基于一次二阶矩阵法的验算点基础上的,忽略二阶以上的高价项,(5)式可表示为 (6) 在验算点在失效边界上,g(x*)=0,则: (7) (8) (9) (9)式表示为矢量的形式为: (10) (11) (12) 2.2.2 可靠指标矢量表示失效模式间的相关性 以两个失效模式为例说明可靠指标矢量如何表示失效模式间的相关性。 设两个失效模式的极限状态方程分别为: G1=a0+a1x1+a2x2+…+anxn (13) G2=b0+b1x1+b2x2+…+bnxn (14) 式中,ai,bi为系数。xi为一组相互独立的随机变量,均值为μ(xi),均方差为σ(xi)。若干个专家对两个失效模式发生概率经验估计的均值和标准差记为μGi和σGi(i=1,2),则相关系数可以表示为: (15) 对G1、G2,可靠指标矢量分别表示为 (16) (17) (18) (19) 以上分析过程都是假设各个基本随机变量服从正态分布,当随机变量不是正态分布时,可以采用映射变化法或当量正态化方法将非正态随机变量转化为正态随机变量[19],具体转换过程见参考文献[20]。通过以上分析发现利用可靠指标矢量计算各个失效模式间的相关性是很方便的,但是是基于各随机变量相互独立的假设,若随机变量间存在相关性,要进行不相关性转换后再进行可靠指标矢量的计算,不相关性转换过程见参考文献[21]。 2.3 基于概率网格估算的失效模式替代 概率网格估算方法(Probability Network Evaluation Technique,PNET)用于技术创新风险管理中的失效模式排序与替代的基本原理是所有的失效模式可用m个主要模式来代替。这些主要失效模式的选择原则为:把所有失效模式分为几组,在同一组中各失效模式与该组中主要失效模式的相关性ρij满足ρij≥ρ0,且这一主要模式在该组所有失效模式中发生的概率最大,可代表该组所有失效模式的发生概率[22]。 根据PNET法的原则,设n个失效模式中,第i个失效模式的发生概率为pfi,则技术创新的成功概率为: (20) 对应的失效概率为: (21) 当Pfi很小时,式(18)可以近似的写成: (22) 为验证本文改进的FMEA方法的可行性,将该方法应用于一个一般的技术创新风险管理过程,并与传统FMEA方法进行比较。 3.1 传统FMEA方法的结果 根据传统FMEA方法分析流程:首先由技术创新负责人组织相关人员将技术创新过程分为创新思想产生、R&D及商业化三个阶段,并对各个阶段进行任务分解(R&D阶段细分为项目定义和设计研发两个任务;商业化阶段细分为技术产品化及营销两个任务),得出各流程可能的失效模式及其影响因素(采用文献[23]中实证得出的29个因素)。然后确定S、O、D(具体见图3)。接下来在对资料和数据进行初步处理后,输入RELEX软件进行计算。同时,确定RPN≤5000为可接受风险,且企业有限的资源最多可进行5项风险的处理。RELEX软件得出企业技术创新FMEA分析表图如图3,绘制出RPN雷达图如图4。 图3中发现max{RPN(Mi)}=3000<5000,均为可接受风险。根据图4,企业在资源有限的情况下需处理的5项失效模式为:技术转化成产品失败(M9);创意演化失败(M2);产品不适宜批量生产(M10);项目周期规划不合理(M4);组建团队与项目要求不匹配(M6)或收入达不到预期水平、时间延迟、费用增加(模式8)。企业可根据图3中列出的失效模式后果及其影响因素分析,制定相应的风险管理措施,但是RPN(M6)=RPN(M8),企业不能确定应对哪个模式进行处理。 图3 技术创新风险管理的传统FMEA分析表图 3.2 改进FMEA方法的结果 图4 传统FMEA方法RPN值 在运用传统FMEA方法计算出各个失效模式的RPN值之后,按照RPN值从大到小的顺序对失效模式的排序为M9>M2>M10>M4>M6=M8>M7>M1=M5>M11>M3,排序后,RPN值从大到小的各失效模式对应的代码见表1。运用改进FMEA方法中失效模式相关性的计算方法,计算出Ri(i=1,2,…,11)之间的相关性系数ρij(见表2)。同时,从图3中可以看出失效模式之间包含共同的风险因素,验证了ρij存在的有效性。假设企业技术创新中相关决策者为中性(既不保守也不激进),其确定ρ0=0.5。运用概率网格估算法进行失效模式替代后,得到主要失效模式代码为R1、R7、R8,对应的失效模式分别为:R1对应技术转化成产品失败(M9)、R7对应技术问题解决失效(M7)、R8对应消费者潜在需求挖掘失败(M1)。企业只需根据图3中M9、M7、M1产生的后果及其影响因素制定相应的风险管理措施即可。 表1 排序后失效模式的对应代码 表2 失效模式相关系数 ρijR1R2R3R4R5R6R7R8R9R10R11R110.570.510.550.580.570.360.320.550.230.21R21000.70.560.570.37000R310.4400.5600.430.340.360.34R410.50.680.420.360.90.470.9R510.330.560.36000R610.110.250.680.230.78R710.340.5200.22R810.330.550.78R910.080.8R1010.76R111 3.3 结果分析 通过案例分析发现改进的FMEA方法得出了企业技术创新过程中需优先进行处理的3个主要失效模式分别是M9、M7、M1,其中,M9是商业化阶段的风险,M7是R&D阶段的风险,M1是是创新思想产生阶段的风险,这三个风险能有效代表技术创新全程的风险。与传统FMEA方法相比较,传统方法得出的需优先处理的风险为:M9、M2、M10、M4、M6或M8。从图3中影响因素的包含关系可以看出:M2、M10、M4、M6、M8与M9相关性较大,可包含于M9中,而另外两个非常重要的风险M7和M1传统方法却没有考虑到。因此,改进的FMEA方法基于失效模式间相关性来进行失效模式的替代,剔除了传统FMEA方法中可能重复处理的风险,同时扩大了风险的防范范围,既能节省企业资源,又能提高风险管理效率,是企业有效的技术创新风险管理定量分析工具。 基于合理的猜想,从结果优化角度,本文提出了一个用于企业技术创新风险管理的改进的FMEA方法。其改进点是在传统FMEA方法基础上,基于失效模式相关性进行失效模式的替代,能得出技术创新过程中主要失效模式。通过一个一般技术创新过程的案例分析表明:在企业资源有限的情况下,运用改进的FMEA方法进行技术创新风险管理,既能节省企业资源,又能提高企业技术创新风险管理效率,是企业有效的技术创新风险管理定量分析工具。本文仅从优化FMEA结果角度提出了改进方法,由于在运用FMEA进行技术创新风险管理过程中,需大量相关专家的经验判断及经验数据,在实践中,可结合文献[10]~[15]中有关FMEA分析过程改进的方法,过程与结果同时改进的FMEA方法能最准确的得出结果,为企业进行技术创新风险管理提供理论依据。同时,将过程和结果优化结合起来的改进的FMEA方法的分析和应用是下一步需研究的问题。 [1] Carl L P. Risk management[M]. Arlington, Virginia, USA: ESI International, 1999. 215-217 [2] 吴涛.技术创新风险管理的方法与策略[J].科学学与科学技术管理,2000,21(5):45- 47. [3] 周寄中,薛刚.技术创新风险管理的分类与识别[J].科学学研究,2002,20(2):221-224. [4] 陈勇飞.FMEA简介[J].机械工程师,2002,(1):31-35. [5] 奚立峰,徐刚.FMEA在过程管理中的应用[J].工业工程与管理,2002,(1):37-39. [6] Stamatis D H.故障模式影响分析:FMEA从理论到实践[M].北京:国防工业出版社,2005:23,171-226. [7] Ben D M, Raouf A. A revised failure mode and effects analysis model[J]. Quality Reliability Managmet, 1993, 3(1): 43- 47. [8] Gilchrist W. Modeling failure modes and effects analysis[J]. Quality Reliability Management, 1993, 10(5): 16-23. [9] Xu K, Tang L C, Xie M, et al. Fuzzy assessment of FMEA for engine systems[J]. Reliability Engineering and System Safety, 2002, (75): 17-29. [10] Keller A Z, Kara Z C. Further application of fuzzy logic to reliability assessment and safety analysis[J]. Microelectron Reliab, 1981, (29): 399- 404. [11] Bell D, Cox L, Jackson S, et al. Using causal reasoning for automated failure and effects analysis(FMEA)[C]. Proceedings of Annual Reliability and Maintainability Symposium,1992. 343-353. [12] Bowles L, Pelaez K. Fuzzy logic prioritization of failures in a system failure modes, effects and criticality analysis[J]. Reliability Engineering System Safety, 1995, (50): 203-213. [13] Chang C L, Wei C C, Lee Y H. Failure mode and effects analysis using fuzzy method and grey theory[J]. Kybernetes, 1999, 28(9): 1072-1080. [14] Anand P, Jin W. Modified failure mode and effects analysis using approximate reasoning[J]. Reliability Engineering and System Safety, 2003, (79): 69- 85. [15] Antonio C F, Guimaraes H, Celso M F L. Effects analysis fuzzy inference system in nuclear problems using approximate reasoning[J]. Annals of Nuclear Energy, 2004, (31): 107-115. [16] 王立新,李勇,任荣明.基于灰色多层次方法的企业技术创新风险评估研究[J].系统工程理论与实践,2006,(7):98-104. [17] 贡金鑫.仲伟秋.赵国藩,结构可靠指标的通用计算方法[J].计算力学学报,2003,20(1)12-18. [18] 孙海.结构体系抗震可靠度的优化与控制研究[D].哈尔滨工程大学博士学位论文,2009. [19] 侯钢领,欧进萍.结构可靠指标矢量及其计算与应用[J].计算力学学报,2002,(2):143-147. [20] 段宇博.高层建筑结构的可靠度分析与优化设计[D].哈尔滨建筑大学博士学位论文,1994. [21] 邵光信,亚海斌,朱绳武.基于GA和PNET的一种可靠度计算新方法[J].金属矿山,2002,(8):51-53. [22] 陈劲,景劲松,童亮.复杂产品系统创新项目风险因素实证研究[J].研究与发展管理,2005,17(6)62-69. Improvements of FMEA Method and Its Applications to the Risk Management of Technology Innovation LUO Xiao-fang1, LI Bai-zhou2, BAI Xu3 (1.SchoolofEconomicsandManagement,JiangsuUniversityofScienceandTechnology,Zhenjiang212003,China; 2.SchoolofEconomicsandManagement,HarbinEngineeringUniversity,Harbin150001,China; 3.SchoolofNavalArchitecture&OceanEngineering,JiangsuUniversityofScienceandTechnology,Zhenjiang212003,China) Because of limited resources, the identification and protection of main risk is the key to risk management of enterprise technology innovation. Firstly, based on reasonable guesses and from the results optimization, we put forward an improved FMEA method based on reliable index vector-probability grid estimation, that is, failure modes are substituted in terms of their correlations, and then find out the main failure modes. Moreover, the improved FMEA method is applied to a risk management case of technology innovation, and the obtained results are compared with the traditional FMEA method. We conclude that our improved FMEA method used for risk management can not only save resources of enterprise, but also improve the efficiency of risk management. It is an effectively quantitative tool for risk management of enterprise technology innovation. innovation risk control; FMEA; reliable index vector; probability grid method; 2013- 03- 04 国家自然科学基金青年基金资助项目(51409128,71402065);国家社科基金重点项目(14AGL001);江苏省高校自然科学研究项目(14KJB57001);江苏高校哲学社会科学研究一般项目(2014SJB818);镇江市软科学项目(RK2014034);国家自然科学基金资助项目(71073034);中央高校基本科研业务费专项资金项目(HEUCF130909) 罗小芳(1987-),女,湖南浏阳人,博士,研究方向为科技管理与创新管理;李柏洲(1964-),男,辽宁彰武人,教授,博士,博士生导师,研究方向为科技管理与创新管理;白旭(1984-),男,江苏徐州人,博士,研究方向为船舶与海洋工程风险评估及管理。 F224.9 A 1007-3221(2015)06- 0264- 08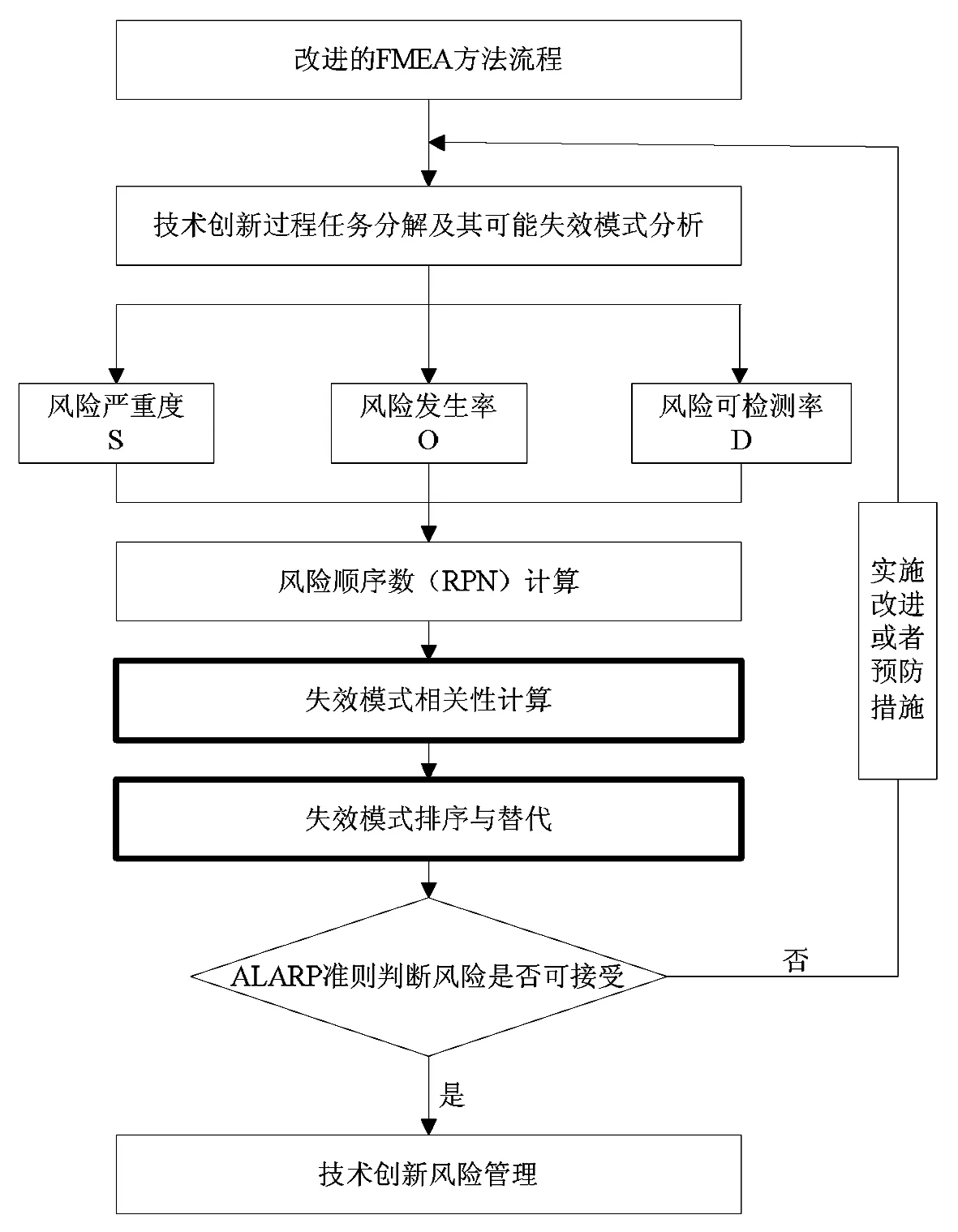
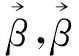
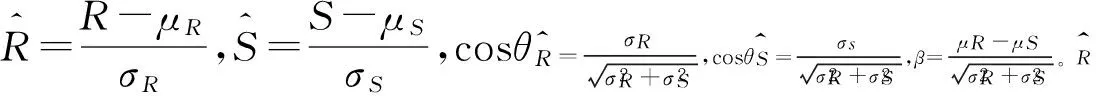
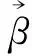
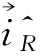
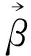
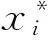
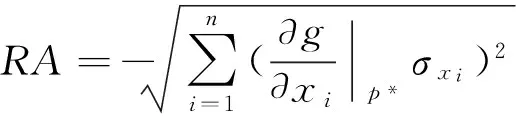
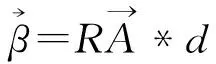
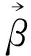
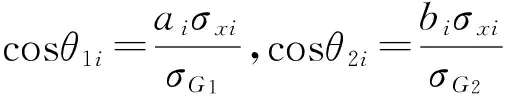
3 应用案例分析

4 结束语

