模糊环境下动态供应商选择的混合整数非线性规划模型

陈浩东， 王志平， 陈 燕

(1.大连海事大学 交通运输管理学院; 2.数学系，辽宁 大连 116026)



模糊环境下动态供应商选择的混合整数非线性规划模型

陈浩东1， 王志平2， 陈 燕1

(1.大连海事大学 交通运输管理学院; 2.数学系，辽宁 大连 116026)

基于供应商选择问题的动态性和模糊性，考虑在每个周期内生产商的需求能力及供应商的供应能力为模糊变量，本文将一个多阶段多商品多渠道的供应商选择问题视为一个0-1混合整数模糊动态非线性规划问题，目标函数为总成本最小化。然后建立了0-1混合整数模糊动态非线性规划模型。为了求解该模型，通过可信性理论把模型中模糊机会约束清晰化，将该模型转化为一个确定型的0-1混合整数动态非线性规划模型。最后给出了一个数值算例验证了模型的可行性。

动态供应商选择;模糊机会约束;混合整数非线性规划;可信性理论

0 引言

在当今激烈竞争的动态环境中，随着经济全球化进程的推进,产品更新换代的速度不断加快，供应商在企业生产中的地位和作用不断增强。因此，动态供应商选择问题日益引起了人们的关注，逐渐成为国内外学术界研究的一大热点。

供应商选择方法的研究大致经历了三个发展阶段:定性方法、定量方法、定性与定量相结合的方法。早期的供应商选择方法采用定性方法,它主要根据以往经验和与供应商关系进行主观判断,由于缺乏科学依据和主观性太强而逐渐被采购管理者抛弃,但在一些小规模、起步阶段的公司里仍然广泛存在, 具有操作简单、节省费用等优点[1]。自从1915 年美国的电气工程师Harris首先提出经济订货批量(Economic Order Quantity, EOQ )模型后,Wilson提出了同样的公式分析了企业库存控制方面各种可能的应用,由此而演变为各种扩展的模型。这时人们采用定量方法来选择供应商,目标是确定采购的经济批量以减小成本。不久,人们发现影响供应商选择的因素有很多,仅仅从库存成本的角度选择供应商是远远不够的。Dickson[2]调查170个采购代理和采购管理者的采购实践总结出23条有关供应商选择准则。Weber等[3]扩展了Dickson的研究成果,通过对74 篇有关供应商选择文献的分析发现:大多数文章中都提到了价格、交货期、质量和能力准则,尤其在JIT(just in time, JIT) 采购中强调运输距离及准时交货的重要性,得出供应商选择问题是一个相互冲突的多准则问题的结论。例如较低的采购价格可能导致质量和交货可靠性的降低等,采购决策者必须权衡这些冲突的目标,选择合适的供应商并合理分配采购数量[4]。此后,供应商选择理论与方法的研究转向定量与定性相结合的方法。目前,关于供应商选择的定量和定性相结合的模型大致包含三大类[5]：(1)多属性决策法：包括层次分析法、网络分析法、优先组织排名改进评估法、逼近理想解排序法(TOPSIS)、简单多属性评估法(SMART)等；(2)数学规划模型：包括数据包络分析(DEA)、线性规划、非线性规划、多目标规划、目标规划、随机规划等；(3)人工智能技术：有遗传算法、灰色系统理论、神经网络、粗糙集理论、基于案例推理(CBR)、粒子群算法、蚁群算法、模糊集理论(FTS)等。本文采用非线性规划模型和模糊集理论研究动态供应商选择问题。

动态供应商选择是供应链管理的一个最重要环节，近年来受到许多专家和企业的关注，其中对供应商选择问题研究最早、影响最大的是Dickson[2],随后许多供应链管理专家对其进行了研究。Sucky[6]从企业投资花费的角度，依据线性规划理论和方法，提出了单目标动态战略供应商选择模型，选择企业的战略合作伙伴。Liao和Rittscher[7]把供应商选择、批量采购和选择运营商决策整合在一起，然后建立了多目标动态规划模型，但该模型考虑的生产商在每个阶段的需求量是已知的。Li等[8]提出了随机动态规划供应商选择模型，同时考虑了混合策略，采购承诺和合同取消的情况。基于蚁群仿真智能算法，Tsai等[9]研究了在动态商业环境中供应商选择的决策方法，给出了模型的算法和使用条件。针对供应商选择和订单分配问题，Mafakheri等[10]提出了一个双阶段多目标动态规划方法。Ventura等[11]考虑多个供应商和一个制造商的二级供应链，提出了针对单一产品的多周期库存批量生产模型。Nilesh等[12]基于供应商选择问题的动态性，提出了混合整数非线性规划模型，数值验证了模型的可行性。文献[6-12]虽然对动态供应商选择问题作了细致研究，但是这些文献均没有考虑动态供应商选择问题中一些变量的模糊性以及不确定性。

在供应商选择的实际问题中，由于各种原因导致供应商和生产商之间的信息不完全共享，从而彼此之间的信息存在一定的模糊性以及不确定性。为此，许多学者尝试建立模糊规划模型解决遇到的这一问题。赵娟和陈华友[13]基于模糊需求量信息，对于多产品供应商问题建立了模糊多目标规划模型。刘诚等[14]考虑供应商的供应能力和生产商的需求能力为模糊参数，给出了一个模糊线性规划模型。Amid等[15]研究供应商选择问题，为了克服选择过程中一些信息的不确定性，建立模糊多目标模型。Arikan[16]在已有文献的基础上，考虑了决策者满意度，并且建立一个模糊多目标供应商选择模型。但是文献[13-16]没有研究供应商选择问题随时间变化而导致的动态性。

基于上述文献均没有同时考虑供应商选择问题的动态性和模糊性，本文在现有文献的基础上，对各供应商的供应能力和制造商的需求量既考虑了各自的模糊性又考虑在每个周期内各自的动态性，建立了动态供应商选择的0-1混合整数模糊非线性规划模型，然后利用可信性理论对该模型进行了求解，数值算例验证了模型的可行性。

1 问题的提出

在实际问题中，往往存在许多不确定因素，为了使问题更加贴近实际，本文研究的多阶段多商品多渠道的动态供应商选择问题考虑供应商供应量和生产商的需求量均为模糊数，同时考虑产品需求的周期性(动态性)。其中本文考虑的周期主要指时间的阶段性，企业在每个阶段都有自身的生产计划，将每个阶段假设为一个周期，各周期之间在时间上连续的，在需求上是独立的。这个动态供应商选择问题可用图1描述如下。通过图1可以看出，动态供应商选择的目的是同时实现企业在多周期内的多渠道多产品的供应商选择和订单分配问题，并且实现各个周期内总花费的最小化。而传统供应商选择问题考虑的只是其中的一个周期，不具一般性。

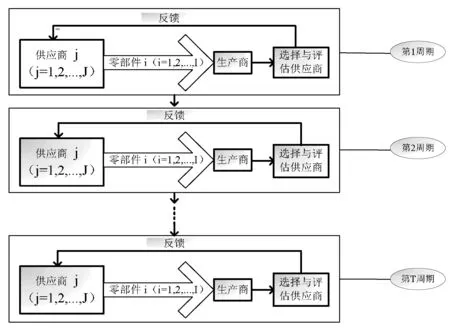
图1 动态供应商选择问题

本文的问题是如何给出一个动态供应商选择方案，确定以下三个问题：(1)生产商在某一时间周期t内需要从哪些供应商预定(或购买)零部件i；(2)根据生产商在周期t内对零部件i的模糊需求量，确定这些零部件分别需要采购的数量是多少；(3)生产商在周期t内需求的某一零部件i应该选择哪些供应商供应，使生产商在各个周期的模糊需求量尽量满足，并且使所产生的总成本最小。

2 建立模型

为了得到该问题的数学模型，引入0-1变量Yijt，其含义如下：

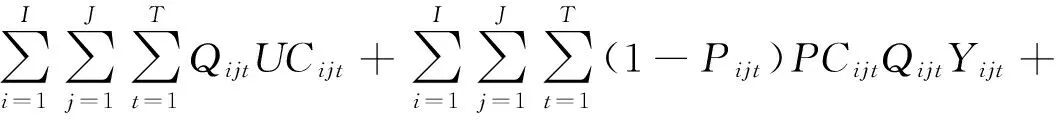
(1)

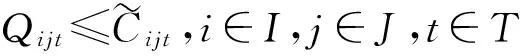
(2)

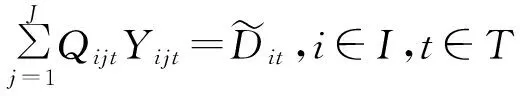
(3)

Pijt≥P0,i∈I,j∈J,t∈T

(4)

Qijt≥0,i∈I,j∈J,t∈T

(5)

Yijt={0,1},i∈I,j∈J,t∈T

(6)

3 模型求解

3.1 模型转化

模型Ⅰ是一个带有模糊约束条件的0-1混合整数动态非线性规划模型，由于该模型存在模糊变量，使得约束条件(2)和(3)没有明确的意义。为了求解该模型，必须进行合理地转化，基于文献[10]和文献[13]的研究基础，模型Ⅰ可以转化为一个模糊机会约束的混合动态非线性规划模型即模型Ⅱ:

模型Ⅱ minZ

(7)

(8)

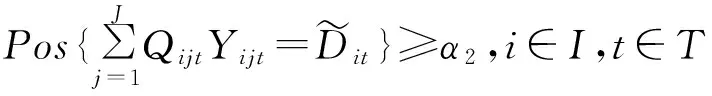
(9)

Pijt≥P0,i∈I,j∈J,t∈T

(10)

Qijt≥0,i∈I,j∈J,t∈T

(11)

Yijt={0,1},i∈I,j∈J,t∈T

(12)

Pos{X}表示{X}中事件成立的可能性。公式(8)和(9)分别表示约束条件得到满足的可能性至少应达到给定的置信水平为α1和α2。

3.2 模糊机会约束规划的清晰化

本文采用文献[17]中的α-切割法，将各模糊机会约束转化为相应的清晰等价类，理论依据见引理。

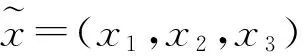
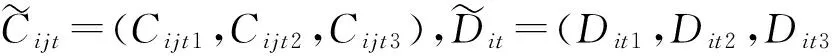
Qijt≤(1-α1)Cijt3+α1Cijt2

(13)

(14)

(15)

由此可得，在将各供应商的供应量和生产商的需求量看成是隶属度函数已知的三角模糊数的前提下，模型Ⅱ中的模糊机会约束(8)和(9)可以转化为各自的清晰等价类。因此可以得到模型Ⅲ：

模型Ⅲ minZ

(16)

s.t.Qijt≤(1-α1)Cijt3+α1Cijt2

(17)

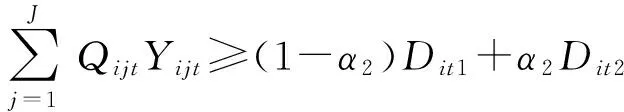
(18)

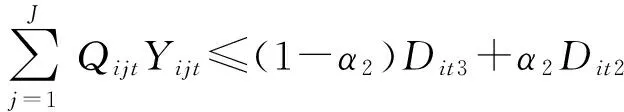
(19)

Pijt≥P0,i∈I,j∈J,t∈T

(20)

Qijt≥0,i∈I,j∈J,t∈T

(21)

Yijt={0,1},i∈I,j∈J,t∈T

(22)

模型Ⅲ是一个确定型的0-1混合整数动态非线性规划模型，可以采用现有的方法求解。

4 数值算例

模型Ⅲ可以用软件LINGO 9.0求解。在这个算例中，一个制造公司作为生产商制造了三类不同的产品，这些产品作为最终商品出售之前，还需要三类不同的零部件(分别用P1，P2，和P3表示)进行组装，这些零部件由三家不同的供应商(分别用S1，S2，和S3表示)提供。由于受市场波动和顾客需求等风险因素的影响，生产商对三种零部件的需求量随时间而变化，根据以往经验，生产商知道在各个时间周期内的零部件的模糊需求量。而且，各个供应商对零部件的供应能力由于受到资金和原材料等风险因素的制约，也随时间的变化而变化，根据以往数据，供应商也知道在各个时间周期内对某一零部件的模糊供应量。

算例中,将一年划分为四个时间周期，即T1为1～3月，T2为4～6月，T3为7～9月，T4为10～12月。三个供应商S1，S2，和S3分别供应三类零部件P1，P2，和P3。表1表示4个时间周期内供应商提供的零部件的单位价格，零部件的质量合格率，不合格产品的单位违约花费，延迟供应零部件的数量，延迟供应的单位花费，以及固定运输花费；表2给出了生产商在4个时间周期内对三类零部件的模糊需求量；供应商在4个时间周期内供应零部件的模糊供应量见表3。质量合格率P0设为0.85。

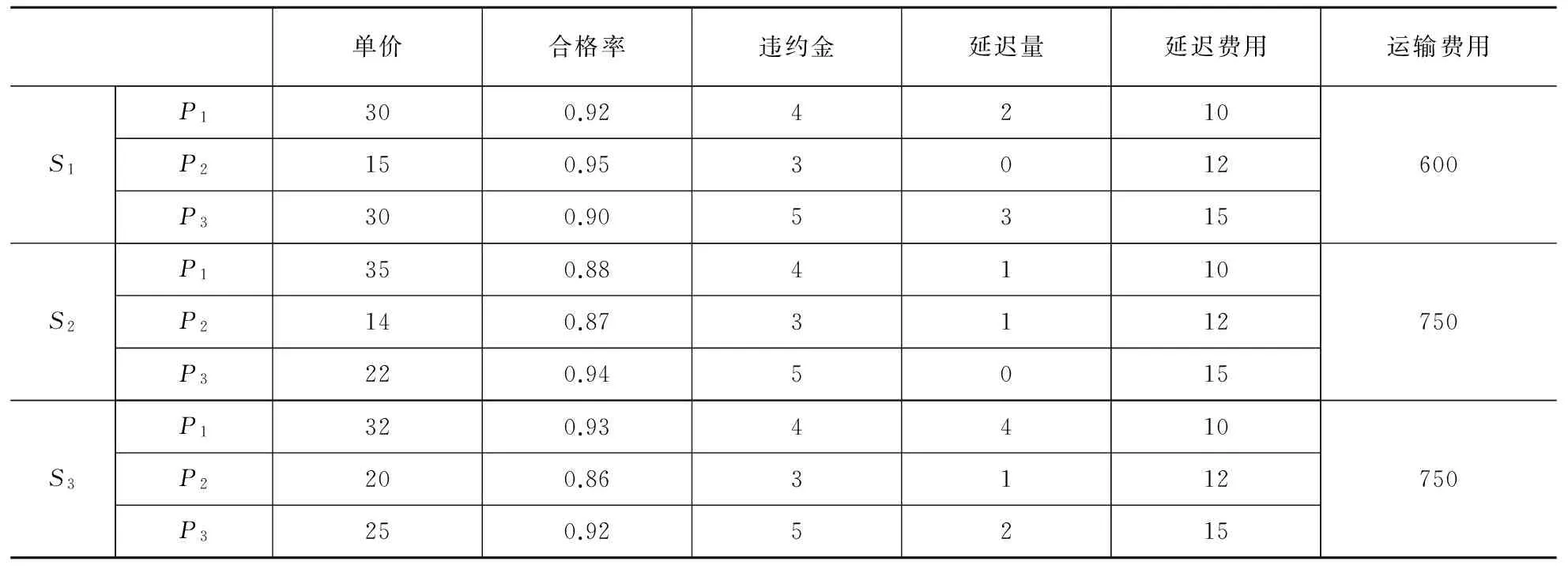
表1 供应商相关数据

表2 生产商在四个周期内的三种零部件的模糊需求量

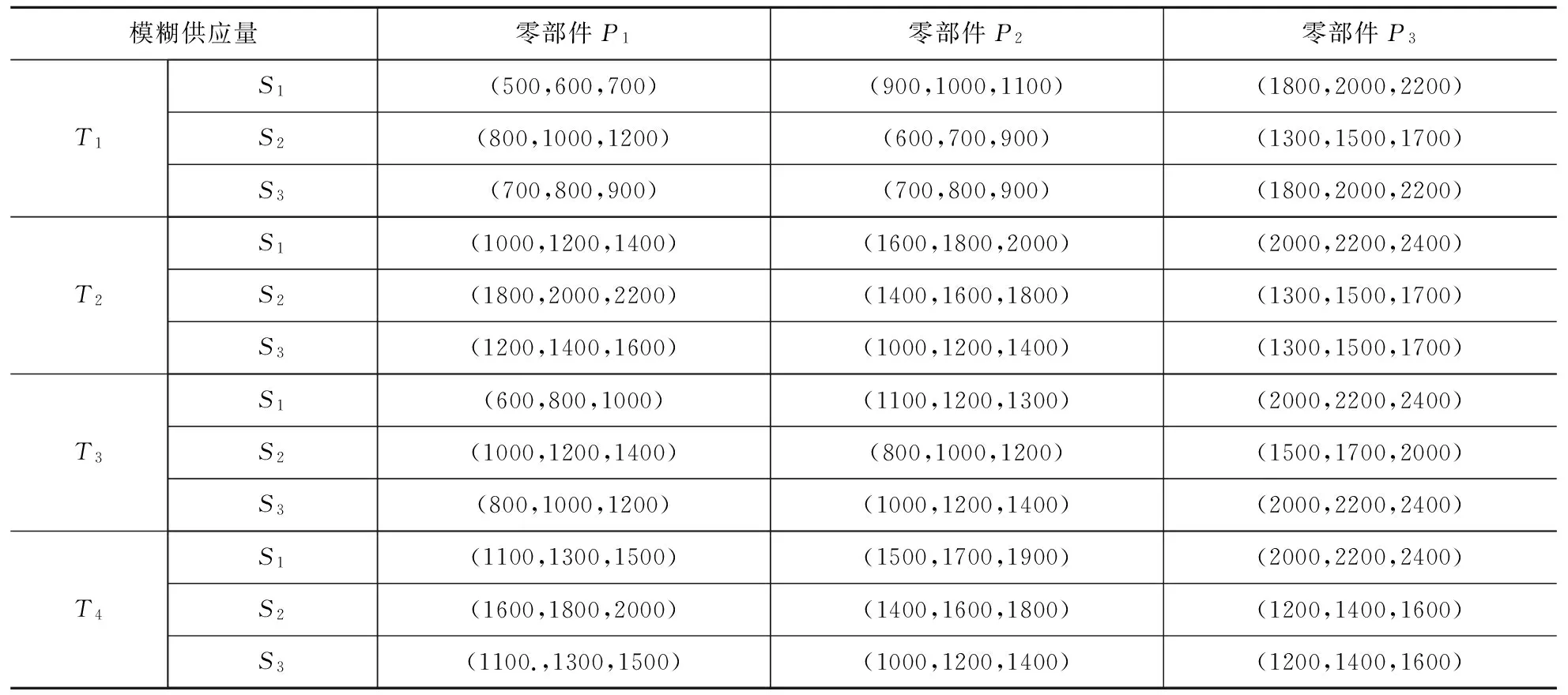
表3 供应商在四个周期内的三种零部件的模糊供应量

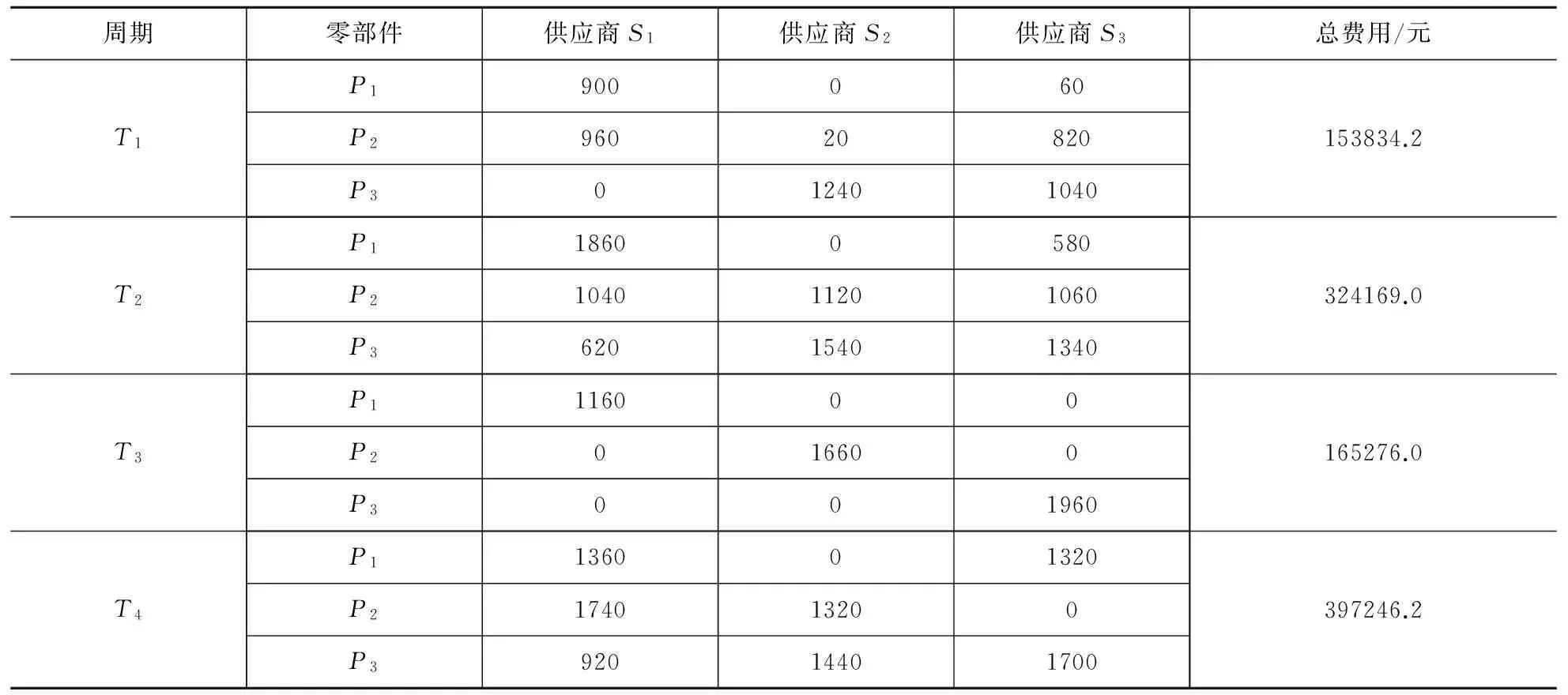
表4 模型Ⅲ的计算结果

通过模型Ⅲ的计算结果可以得出：在第一周期(即1至3月份)，供应商S1供应零部件P1=900件，零部件P2=960件；供应商S2供应零部件P2=20件，零部件P3=1240件；供应商S3供应零部件P1=60件，零部件P2=820件，零部件P3=1040件，总费用为153834.2元。

在第二周期(即4至6月份)，供应商S1供应零部件P1=1860件，零部件P2=1040件，零部件P3=620；供应商S2供应零部件P2=1120件，零部件P3=1540件；供应商S3供应零部件P1=580件，零部件P2=1060件，零部件P3=1340件，总费用为324169.0元。

在第三周期(即7至9月份)，供应商S1供应零部件P1=1160件；供应商S2供应零部件P2=1660件；供应商S3供应零部件P3=1960件，总费用为165276.0元。

在第四周期(即10至12月份)，供应商S1供应零部件P1=1360件，零部件P2=1740件，零部件P3=920；供应商S2供应零部件P2=1320件，零部件P3=1440件；供应商S3供应零部件P1=1320件，零部件P3=1700件，总费用为397246.2元。

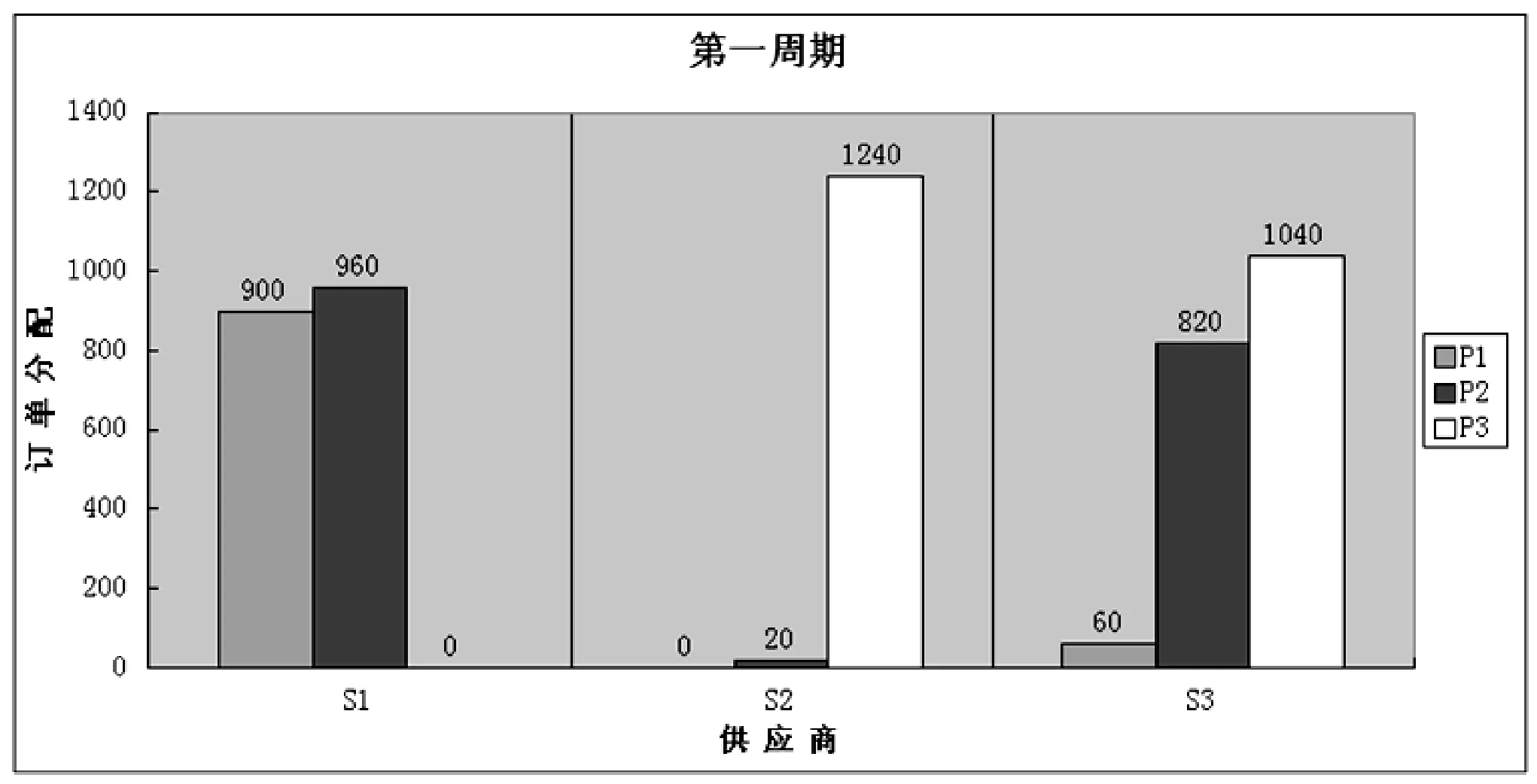
图2 第一周期内的供应商—订单分配

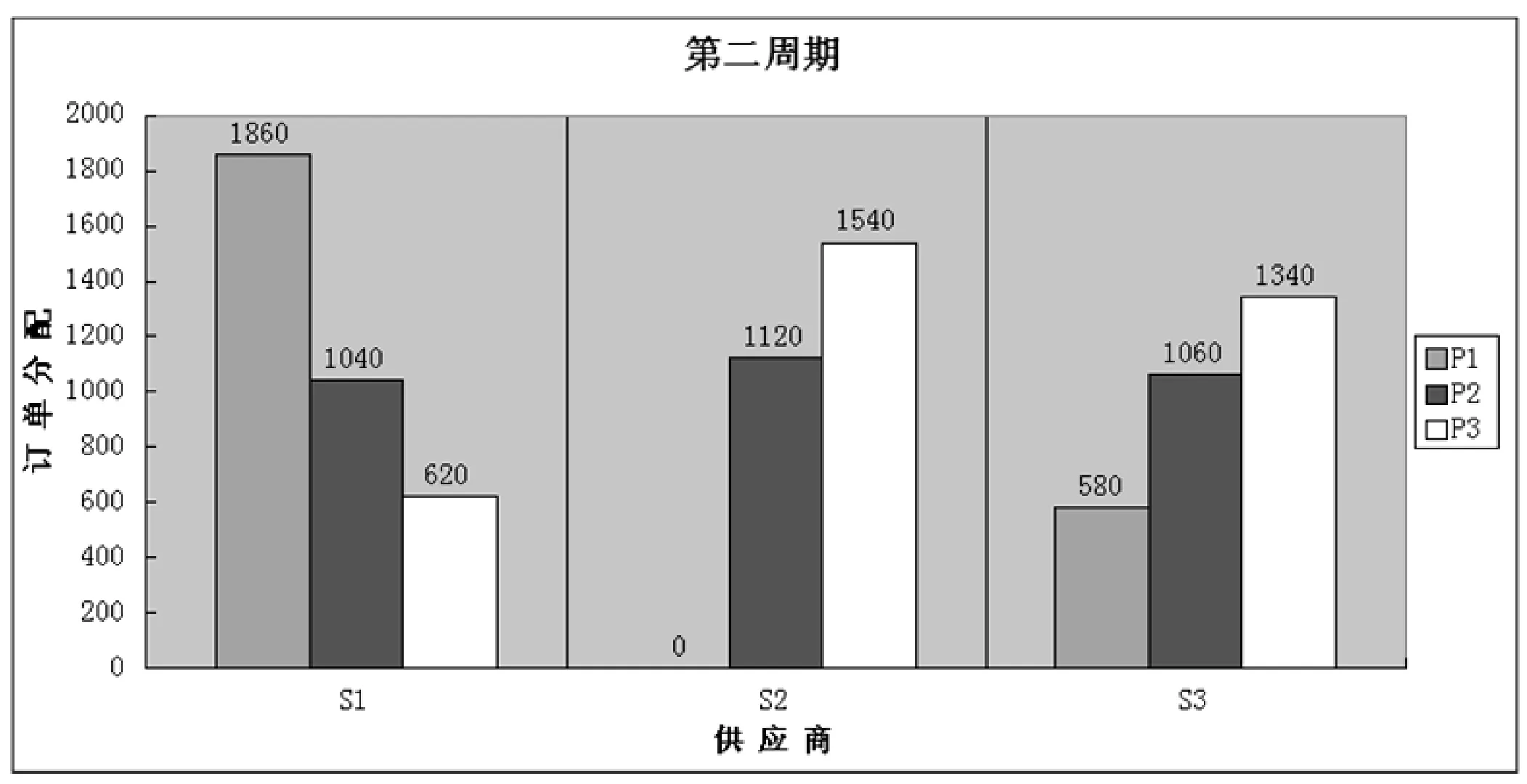
图3 第二周期内的供应商—订单分配

图4 第三周期内的供应商—订单分配

图5 第四周期内的供应商—订单分配

模型Ⅲ中，在T2时对置信水平α进行灵敏度分析。假设置信水平α2=0.8，当α1分别取0.2,0.4,0.6,0.8和1.0时，此时计算结果见图6；假设置信水平α1=0.8，当α2分别取0.2,0.4,0.6,0.8,1.0时，此时结果也见图6。

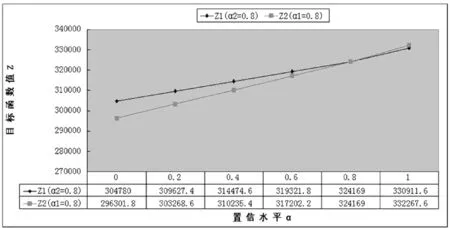
图6 第二周期内置信水平与目标函数值的关系

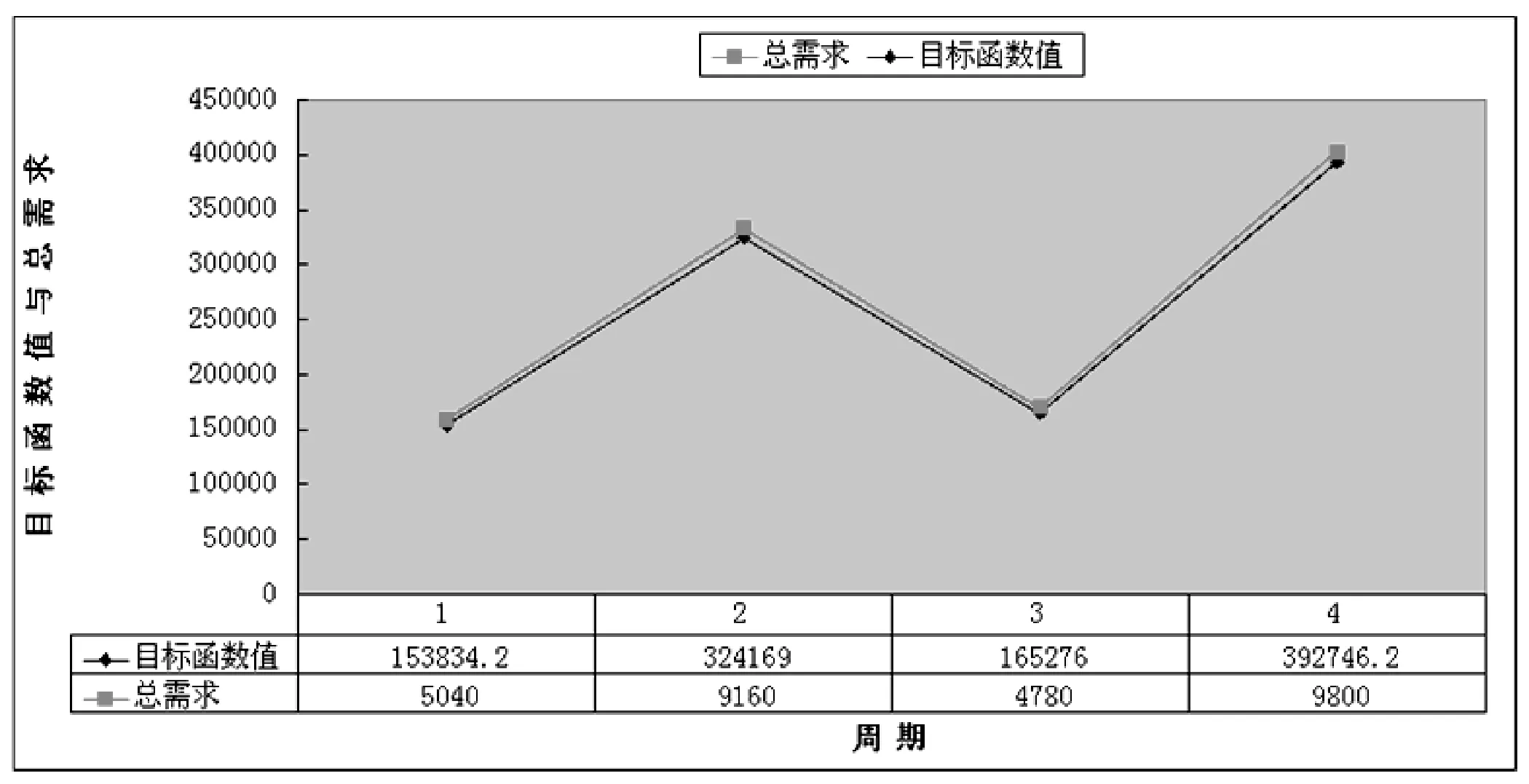
图7 四个周期内零部件总需求和总成本的关系

从图6可以看出，当固定置信水平α1(=0.8)的大小，而改变置信水平α2的大小，随着α2的提高，总成本费用Z2也在逐渐增加。这是因为随着α2的提高，对零部件满足需求的要求也逐渐提高，当α2为1时，生产商的零部件的需求量得到满足，此时，总成本费用最高，这符合实际情况。当固定置信水平α2(=0.8)的大小，改变置信水平α1的大小，随着α1的提高，总成本费用Z1也在逐渐增加，但增速明显低于Z2。这是因为，结合实际情况来说，如果确定了供应商的供应量满足了生产商需求量的最低标准，以及所需总成本的最高限额，则对供应商的供应能力必须高于供应量的要求越高，则零部件的需求量也会有所改变，但变化范围不会太大，所以总成本也不会有大幅变化。从图7可以看出，各个周期生产商对零部件的总需求量与总成本的变化呈现相一致的变化关系，这是因为在各个周期内当其他花费保持不变时，当各类零部件的总需求量增加，总成本花费就增加，反之亦然，这也和实际情况相吻合。

5 结论

本文在已有文献的基础上，给出了动态供应商选择的框架和流程图，考虑供应商选择问题的动态性和模糊性，将生产商的需求量和供应商的供应能力作为模糊变量整合到模型中，建立了0-1混合整数模糊动态非线性规划模型，并利用可信性理论对其进行了合理的转化和求解，进一步对动态供应商选择进行了研究。最后通过一个数值算例仿真模拟了提出的模型，并结合实际进行分析，结果显示可以为决策者提供一个基本依据。未来的研究方向可以考虑中断风险以及库存对动态供应商选择的影响，在这种情况下产品替代和可变生产花费也应该考虑。

[1] 周文坤,蒋文春.基于改进TOPSIS法的供应商选择方法[J].运筹与管理，2005，14(6):39- 44.

[2] Dickson G W. Analysis of vendor selection systems and decisions[J]. Journal of Purchasing, 1966, (2): 5-17.

[3] Weber C A,Current J R,Benton W C. Vendor selection criteria and methods[J]. European Journal of Operational Research, 1991,50: 2-181.

[4] 刘晓,李海越,王成恩,储诚斌.供应商选择模型与方法综述[J].中国管理学,2004,12(1):139-140.

[5] Chai J Y, Liu N K , Ngai W T. Application of decision-making techniques in supplier selection: a systematic review of literature[J] . Expert Systems with Applications, 2013, 40: 3872-3885.

[6] Sucky E. A model for dynamic strategic vendor selection[J] . Computers & Operations Research , 2007, 34: 3638-3651.

[7] Liao Z Y, Rittscher J. Integration of supplier selection, procurement lot sizing and carrier selection under dynamic demand conditions[J]. Int. J. Production Economics, 2007, 107: 502-510.

[8] Li S L, Murat A, Huang W Z. Selection of contract suppliers under price and demand uncertainty in a dynamic market[J]. European Journal of Operational Research, 2009, 198: 830- 847.

[9] Tsai Y L, Yang Y J, Lin C H. A dynamic decision approach fo supplier selection using ant colony system[J]. Expert Systems with Applications, 2010, 37 : 8313- 8321.

[10] Mafakheri F, Breton M, Ghoniem A. Supplier selection-order allocation: a two-stage mul-tiple criteria dynamic programming approach[J] . Int. J. Production Economics, 2011, 132: 52-57.

[11] Ventura J A, Valdebenito V A, Golany B. A dynamic inventory model with supplier selection in a serial supply chain structure[J] . European Journal of Operational Research, 2013, 230: 258-271.

[12] Nilesh R W, Singh S P ,Banwet D K. A mixed-integer non-linear program to model dynamic supplier selection problem[J]. Expert Systems with Applications, 2014, 41: 671- 678.

[13] 赵娟，陈华友.基于模糊需求的多产品供应商选择的多目标规划模型[J].模糊系统与数学，2011, 25(4):148-155.

[14] 刘诚，卢宗娟，梁文冬.模糊环境下供应商选择[J] .系统工程，2011,29(4):104-108.

[15] Amid A, Ghodsypour S H, O’Brien C. Fuzzy multi objective linear model for supplier selection in a supply chain[J]. International Journal of Production Economics, 2006 ,104(2) : 394- 407.

[16] Arikan F. A fuzzy solution approach for multi objective supplier selection[J] . Expert Systems with Applications, 2013, 40(3): 947-953.

[17] 刘宝碇，赵瑞清.随机规划和模糊规划[M] .北京:清华大学出版社，1988.160-172.

Mixed-integer Non-linear Program Model of Dynamic Supplier Selection under Fuzzy Environment

CHEN Hao-dong1, WANG Zhi-ping2, CHEN Yan1

(1.TransportationManagementCollege; 2.DepartmentofMathematics,DalianMaritimeUniversity,Dalian116026,China)

Business of any organization is continuous process and therefore supplier selection problem is dynamic in nature. And firm’s demand and supplier’s capacity for each part changes over time due to market fluctuation and customer demand. Thus supplier selection problem is also fuzzy in real practice. Based on dynamic and fuzziness in nature on supplier selection problem, considering supplier’s capacity and manufacturer’s demand for fuzzy variables in every time period, in this paper, the supplier selection problem for multi-period, multi-parts, and multi-source is considered as a 0-1 mixed integer fuzzy dynamic non-linear programming problem, objective function is minimization of total costs. And then a 0-1 mixed integer fuzzy dynamic non-linear program model is proposed. In order to solve this fuzzy dynamic model, the model is transformed into a deterministic 0-1 mixed integer dynamic non-linear model by converting fuzzy chance constraints to their respective deterministic equivalent formulation by Credibility Theory. A numerical example is illustrated to show that the proposed model is feasible and effective.

dynamic supplier selection; fuzzy chance constrained; mixed-integer non-linear program; credibility theory

2014- 05-13

国家自然科学基金资助项目(70971014);辽宁省自然科学基金资助项目(201102015)

陈浩东(1986-)，男，博士研究生，研究方向：物流与供应链管理；通信作者:王志平(1964-)，男，教授，博士生导师，研究方向：超网络理论，图论，供应链管理等。

F274

A

1007-3221(2015)04- 0128- 09