库存展示量影响需求的促销易腐品最优订货策略
何 伟, 徐福缘
(上海理工大学 管理学院,上海 200093)
库存展示量影响需求的促销易腐品最优订货策略
何 伟, 徐福缘
(上海理工大学 管理学院,上海 200093)
零售商经常会选择多种商品进行促销以提高收益,促销商品与人民群众的日常生活密切相关。本文建立库存影响需求的促销易腐品的订货决策模型,允许缺货发生,且短缺拖后率与已经发生的缺货量和等待时间相关。证明了最优解的存在性和唯一性,提出了求解最优订购策略的搜索算法。通过仿真实验验证模型和算法,得到主要参数的灵敏度分析结果。
库存影响需求;促销商品;变质;模型
0 引言
在经典的库存控制模型中,库存系统的外部需求通常假设为常数,但是实际中市场需求则因为受到诸多因素的影响而发生变化,需求通常会受到物品的库存水平的影响。文献[1]研究了需求依赖即时库存水平的易变质多物品最优订购策略;文献[2]在需求依赖于库存水平下给出了供应商提供延期支付期和量折扣策略的库存模型。文献[3]研究需求率基于库存的变质物品的两货栈模型。有很多学者则基于库存影响需求下的库存模型进行了深入的研究[4~8]。
促销商品是大卖场用来吸引顾客前来购买从而提高商场总销售额的常用营销手段[9]。而实际中卖场为了吸引顾客光顾,促进其它商品销售,一般会选择消耗量大、购买频率高的蔬菜水果等农产品作为促销商品推出,如沃尔玛、家乐福、永辉超市等的天天低价策略,文献[10,11]指出这类产品由于腐烂变质等原因随着时间的推移发生数量和价值方面的损耗。文献[12]提出了电子商务零售中经常会选择多种商品进行促销以提高零售收益。文献[13]研究了等待时间和缺货量的共同影响,认为当接近下次补货点时,由于等待时间较短,顾客一般愿意等待,而此时缺货量较大,如商品补货能力受限,顾客则不愿意等待,但没有考虑促销商品的特点,即库存影响需求和顾客等待时间。
促销商品的销售量较大,缺货时有发生,在传统的库存系统研究中,一般假设短缺不允许发生[14,15],文献[16]假设允许缺货,提出了短缺量完全拖后和部分拖后的库存控制模型,文献[17]对文献[16]中的前两个模型进行理论证明,但是未对模型三进行理论证明,本文从理论上解决了模型三最优解的存在性和唯一性问题。
本文建立库存影响需求的促销易腐品的订货决策模型,根据促销商品的特点,允许缺货发生,且短缺拖后率与已经发生的缺货量和顾客等待时间相关;通过分析,在理论上证明了各种情形下的模型最优解的存在性和唯一性,并提出了求解最优订购策略的搜索算法。最后,通过仿真实验验证模型和算法,并对主要参数进行了灵敏度分析,为销售商制定采购计划和经营决策提供理论依据。
1 模型假设与记号
在以下的分析过程中,使用的主要假设与记号如下:
(1)瞬时供货,提前期为零;
(3)假设物品易腐率θ是一个常数,0≤θ≤1,物品变质后无残值;
(4)允许缺货,且短缺量拖后率函数为:D1(t)=α-γS(t),t1≤t
(5)S(t)表示t时刻等待供货的需求量;
(6)Q是单周期的订货量,S为单周期内的最大缺货量;
(7)T为订货周期,t1表示不缺货的区间长度,t2表示缺货的区间长度,显然T=t1+t2,三者均可作为决策变量,但决策变量实为其中任意两者;
(8)K表示订货费,c是单位商品的购买费用,p是单位商品的销售价,h表示单位商品的库存保管费用,s是商品单位时间的缺货费用,r表示因缺货造成缺销商品的机会成本;M为系统最大库存量;
(9)P(t1,T)为系统的单位时间平均利润。
2 模型建立
根据假设可知在[0,t1]内的库存水平随着需求而下降,因此表示库存水平的状态方程为
(1)
由边界条件I(t1)=0,得微分方程(1)的解
(2)
(3)
缺货期内等待需求量S(t)满足下面的微分方程
(4)
由边界条件S(t1)=0可得(4)式的解
(5)
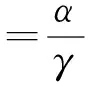
(6)
由此计算一个订货周期T内各项成本如下:
订货成本:K
库存成本:
缺货成本:
短缺拖后供给成本:
订购成本:
销售收入:
所以,系统的平均利润:
P(T,t1)={TR-TCh-TCs-TCr-cQ-K}/T
带入化简可得:
(7)
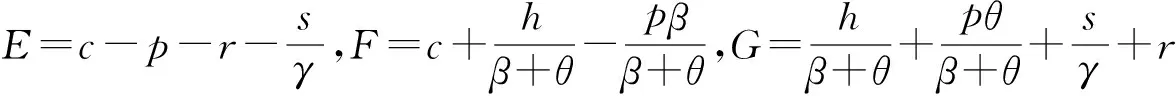
因此,这种库存展示量影响需求的促销易腐品的最优订货策略问题被抽象为下列有约束非线性规划问题:
maxP(T,t1)
(8)
3 模型求解
通过分析 , 可以得到以下关于非线性规划问题 (8) 最优解的一些理论分析结果。
对P(T,t1)关于t1求导可得:
(9)
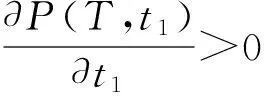
(10)
将(10)式带入(7)式可得
(11)
将(11) 式对t2求导可得
(12)
其中
(13)
由(13)式易得到
(14)
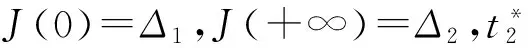
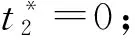
(2)当F>0时,分析如下三种情况:
①当没有短缺发生时,即T=t1,此时有
(15)
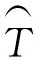
(16)
②当系统一直缺货时,即t1=0,此时有
(17)
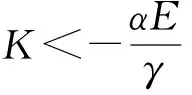
(18)
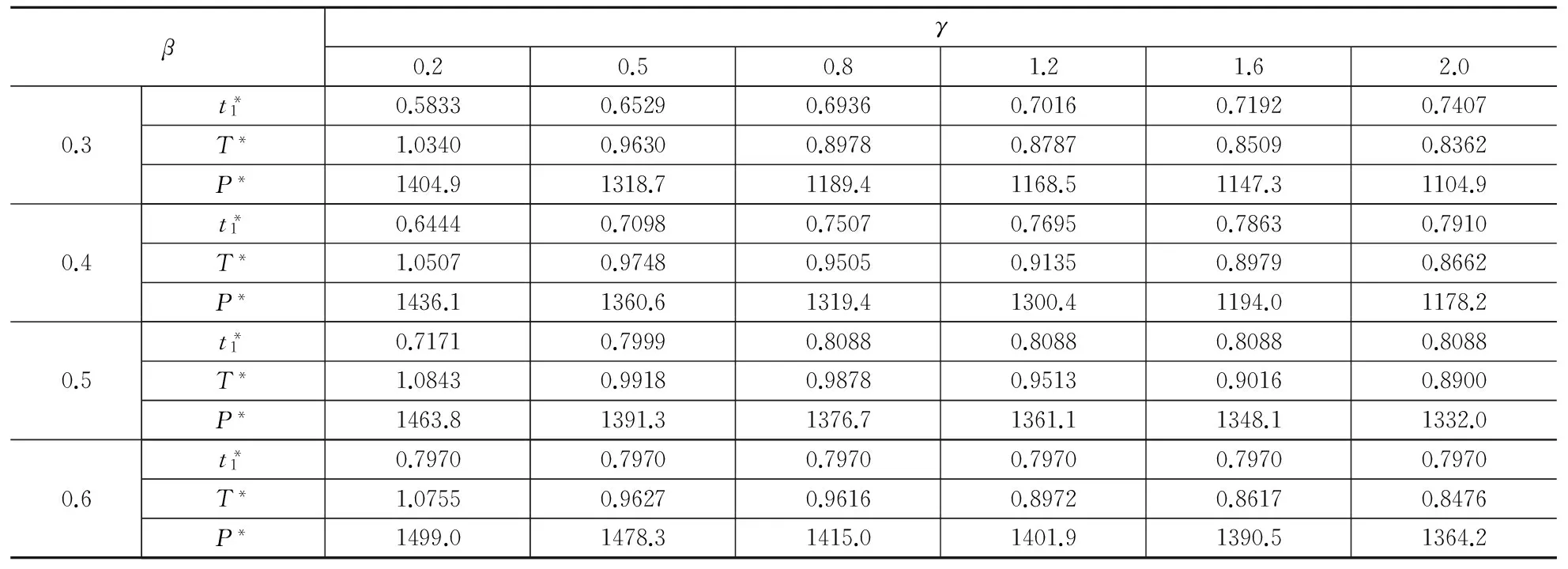
③当0 综合上述分析,可以得到如下定理: 综合所述,求解模型(8)的算法如下: 第1步 输入所有参数的值,计算E,F,G. 根据某大型超市的销售实际情况,在两种情形下模型参数分别设定如下: 模型灵敏度分析如下,通过改变参数β,M的取值,分析利润的变化规律,结果见表1。 表1 F≤0情形下的灵敏度分析 模型灵敏度分析如下,通过改变参数β,γ的取值,分析利润的变化规律,结果见表2。 表2 F>0情形下的灵敏度分析 本文将Padmanabhan & Vrat提出的变质物品库存模型应用到现实零售业销售情形中,考虑促销商品的特点,提出了促销易腐商品的订货决策模型,并且完成了模型最优解存在性和唯一性理论上的证明。假设允许缺货发生,且短缺拖后率与已经发生的缺货量相关,建立了以零售商单位时间内平均总利润为目标函数的库存模型。通过对模型的分析,提供了寻求模型整体最优解的搜索算法。仿真实验表明:采用搜索算法得到的订货周期能使得库存系统利润达到最大,并且可以在存储空间限制范围内通过增大库存水平的办法来增加系统的平均利润。本文为企业优化库存管理决策提供了可行方案,但仅仅是针对变质促销商品的库存优化问题,对于随机变质率或者不同销售属性的多物品联合库存优化问题是下一步研究的方向。 [1] 莫降涛,陈桂梅等.需求依赖即时库存水平的易变质多物品最优订购策略[J].系统工程,2011,29(5):98-101. [2] Sana S S, Chaudhuri K S. A deterministic EOQ model with delays in payments and price discount offers[J]. European Journal of Operational Research, 2008, 184(1): 509-533. [3] 梁培培,黄国华等.需求率基于库存的变质物品的两货栈模型[J].运筹与管理,2013,22(2):201-206. [4] Wu K S, Ouyang L Y, Yang C T. An optimal replenishment policy for no instantaneous deteriorating items with stock-dependent demand and partial backlogging[J].International Journal of Production Economics, 2006, 101(2):369-384. [5] 莫降涛,潘义前等.基于二层信用策略且存货影响销售率的库存模型[J].系统工程,2009,27(9):108-111. [6] 黄菲.基于排污税的易腐品生产库存系统最优生产率控制[J].系统管理学报,2013,22(6): 850-854. [7] Urban T. Inventory models with inventory-level-dependent demand: a comprehensive review and unifying theory[J]. European Journal of Operational Research, 2005, 162: 729- 804. [8] Youhua(Frank)Chen, Ye Lu and Xu Minghui. Optimal inventory control policy for periodic-review inventory systems with inventory-level-dependent demand[J]. Naval Research Logistics, 2012, 59(6):430- 440 . [9] 何伟,徐福缘.需求依赖库存且短缺量部分拖后的促销商品库存模型[J].计算机应用,2013,33(10):2950-2953. [10] 徐永锋.易逝品信用支付集中决策订货策略[J].系统管理学报,2013,22(5): 685- 694. [11] 许甜甜,肖条军.基于数量折扣的时滞变质物品库存协调模型[J].系统工程理论与实践,2013,33(7):1690-1698. [12] 程岩.电子商务中商品交叉销售效果分析及其在促销决策中的应用研究[J].管理评论,2012,24(10):59-65. [13] Duan Yongrui, Li Guiping, James M et al. Inventory models for perishable items with inventory level dependent demand rate[J]. Applied Mathematical Modeling, 2012, 36(10): 5015-5028. [14] Dye C Y, Ouyang L Y. An inventory models for perishable items under stock-dependent selling rate and time-dependent partial backlogging[J]. European Journal of Operational Research, 2005, 163(2): 776-783. [15] Zhou Y W, Yang S L. An optimal lot-sizing model for items with inventory level dependent demand and fixed lifetime under the L IFO policy[J]. Journal of the Operational Research Society, 2003, 54(1): 585-593. [16] Padmanabhan G, Vrat P. EOQ models for perishable items under stock dependent selling rate[J] . European Journal of Operational Research, 1995, 86(2): 281-292. [17] Chung K J, Lan S P. A note on EOQ models for deteriorating items under stock dependent selling rate[J]. European Journal of Operational Research, 2000, 124(3): 550-559. The Optimal Replenishment Strategy for Perishable and Off-price Products with Stock-dependent and Capacity Constraint HE Wei, XU Fu-yuan (BusinessSchool,UniversityofShanghaiforScienceandTechnology,Shanghai200093,China) For improving sales performance, multi-items are often selected for promotion. Off-price item is closely related to people’s daily life. We discuss the inventory problem of perishable and off-price items with stock-dependent demand rate. Some customers are more impatient to wait, therefore the sale opportunity is reduced and a bigger shortage leads to a larger loss. The existence of the optimal solution to the model is discussed, and a search algorithm of the optimal order strategy is provided. Simulation experiments are presented to illustrate the model and the main parameters are carried out. stock-dependent demand rate; off-price item; perish ability; model 2014- 06-16 国家自然科学基金资助项目(71171135);上海市一流学科项目资助(S1201YLXK);沪江基金资助项目(A14006);上海市研究生创新基金资助项目(JWCXSL1301) 何伟(1981-),男,安徽滁州人,博士研究生,研究方向:供应链、企业供需网及其管理;徐福缘(1948-),男,浙江绍兴人,教授,博士生导师,主要研究方向:系统工程企业供需网及其管理。 F274;O227 A 1007-3221(2015)04- 0105- 06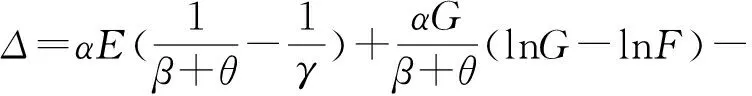
4 模型算法
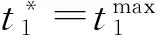
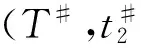
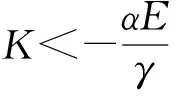
5 数值例子及灵敏度分析
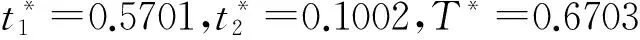

6 结束语
——基于集成射频识别技术

