成品油调和配方优化研究
刘国莉, 叶 同, 王桂玲, 赵 珺
(1.辽宁科技大学 理学院,辽宁 鞍山 114051; 2.大连理工大学 信息与控制研究中心,辽宁 大连 116024)
成品油调和配方优化研究
刘国莉1, 叶 同1, 王桂玲1, 赵 珺2
(1.辽宁科技大学 理学院,辽宁 鞍山 114051; 2.大连理工大学 信息与控制研究中心,辽宁 大连 116024)
成品油调和是石油炼制过程中的重要环节,直接影响炼油企业的经济效益。本文以石化行业为背景,针对成品油调和配方优化问题进行了研究,在满足成品油质量指标约束的条件下,以最小化企业生产成本为目标,建立了混合整数规划模型,提出了基于遗传算法的有效求解策略,并根据某炼油厂的实际生产数据进行了仿真实验,计算结果反映了库存成本与启动成本之间的平衡关系,即:当单位库存成本不变,单位启动成本逐渐变大时,库存总成本随之增大,启动次数随之减少。反之,当单位启动成本不变,单位库存成本逐渐变大时,启动次数随之增大,库存总成本随之减少。
成品油调和;生产库存计划;遗传算法;炼油工业
0 引言
成品油调和是炼油过程中的最后一道工序,也是影响油品质量最关键的工序,它的优化通常是以工艺流程为原理,以生产方案、原油性质、物料平衡、质量指标为约束条件,调和出符合实际需求的成品油。1955年,Nelson[1]提出了用线性规划计算汽油辛烷值的模型。Glismalin和Gruhn[2]针对油品调和问题,建立了非线性调和模型。Jia和Ierapctritou[3]提出了混合整数线性规划模型方法,并利用该方法有效解决了储运调度和油品调和问题。李响[4]针对调和配比模型不够准确和求解速度较慢的问题,建立了新的汽油调和配比模型。罗春鹏和荣冈[5]针对汽油调和生产过程中往往面临诸多不确定因素的问题,建立了一种鲁棒优化模型。江永亨等[6]针对无主炼原油的调和调度问题,建立了相应的数学模型。马义飞和孙晓燕[7]在成品油二次配送体系基础上,建立了配送调度优化数学模型。崔承刚[8]根据油品调和的特点,提出利用可行解和不可行解的活跃约束条件增加辅助函数的方法来加快求解速度。
油品调和就是按照成品油质量指标要求,在满足装置生产能力和成品油需求条件下将组分油作为生产原料加入到产品调和装置生产成品油的过程。因此本文将以石油化工行业为背景,对成品油调和过程进行研究。
1 成品油调和优化模型
在成品油调和过程中,由于汽油和柴油占成品油总量的90%,因此对成品油的调和主要是针对汽油和柴油方面的调和,本文以最小化生产总成本为目标建立成品油调和的混合整数优化模型。
1.1 假设
(1)所有油品的初始库存为0;
(2)炼油厂以按订单生产模式运行,即根据实际需求生产油品;
(3)各种油品独立存储;
(4)成品油的需求已知且相对稳定。
1.2 符号说明
参数:
T—决策区间;
F—组分油的集合;
P—成品油的集合;
hi—单位时间段内采购/生产油品i的单位库存费用,其中i∈F∪P;
Vi—油品i的最大存储量,其中i∈F∪P;
si—在第t个时间段内采购/生产油品i的单位启动成本,其中i∈F∪P;
Pit—在第t个时间段内采购/生产组分油i所需的单位费用,其中i∈F,t∈T;
Dkt—在第t个时间段内成品油k的需求量,其中k∈P,t∈T;
Maxit—在第t个时间段内组分油i的最大使用量,其中i∈F,t∈T;
Capt—在第t个时间段内产品调和装置的最大生产能力,其中t∈T;
ZBi—油品i的质量指标集合,包括辛烷值、柴油凝点、硫含量和烯烃含量,其中的指标用R表示,i∈F∪P;
costk—烯烃的环保成本,其中k∈P;
L—一个很大的正数。
决策变量:
Xit—在第t个时间段内油品i的采购量或生产量,其中i∈F∪P,t∈T;
xikt—在第t个时间段内生产组分油i调入成品油k中的物料量,其中i∈F,k∈P,t∈T;
Iit—在第t个时间段内油品i的存储量,其中i∈F∪P,t∈T;
wit—在第t个时间段内采购/生产油品i时为1,否则为0,其中i∈F,t∈T;
ykt—在第t个时间段内生产成品油k时为1,否则为0,其中k∈P,t∈T。
1.3 数学模型
利用上述假设和符号说明,可将本文所研究的成品油调和问题描述为:
(1)
约束:
Ik,t-1+Xkt-Ikt=Dkt,∀k∈P,t∈T
(2)
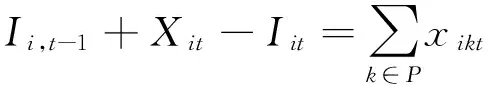
(3)

(4)

(5)Xit≤Maxit,∀i∈F,t∈T
(6)

(7)
0≤Iit≤Vi,∀i∈F∪P,t∈T
(8)
0≤Xit≤L·wit,∀i∈F,t∈T
(9)
0≤Xkt≤L·ykt,∀k∈P,t∈T
(10)
xikt≥0,∀i∈F,k∈P,t∈T
(11)
wit,ykt∈{0,1},∀i∈F,k∈P,t∈T
(12)
目标函数(1)表示成品油调和过程的总成本,由五项组成。其中第一项表示生产成品油时所需组分油的采购/生产成本,第二项和第三项分别表示组分油和成品油的库存成本,第四项和第五项分别表示组分油和成品油的启动成本,最后一项表示烯烃的环保成本。
约束(2)和(3)是库存平衡方程;约束(4)是物料平衡方程;约束(5)表示对成品油中辛烷值、柴油凝点、硫含量和烯烃含量的限制,保证调和出的成品油满足质量指标参数;约束(6)~(8)是对生产能力的限制;约束(9)和(10)限制了组分油和成品油的采购/生产量;约束(11)和(12)是对变量取值范围的限制。
2 遗传算法求解
假设有m种组分油加入的调和装置生产出n种成品油,决策区间为T,参数设计如下:
(1)染色体编码设计:采用浮点型编码方式,每条染色体是一个T*(m+n)矩阵,第t行的前m列表示在第t时间段内组分油的参与量,第m+1列到第m+n列表示在第t时间段内成品油的产量。
(2)构建初始种群:随机产生popsite个个体作为初始种群,每个个体代表着一个周期内组分油的参与量与成品油的产量。
(3)适应度函数的设定:适应度函数一般根据目标函数进行设计。由于本文的模型中需要求的是目标函数f(x)的最小值,因此染色体vk的适应度设为:fitness(vk)=1/(f(vk)+L),其中T为不合理惩罚项,是一个很大的正数。
(4)停止准则:当迭代次数大于设定的最大次数时,终止遗传算法并输出运算结果。本文设定的最大迭代次数G=500。
(5)遗传算子的设计包括:

② 交叉:选取一定的交叉概率pc对染色体采用算数交叉法,设ρk1和ρk2表示第k代中随机选择出的两个染色体,则经过变异操作的后代表示为:θk1=ρk1+(1-α)ρk2,θk2=ρk2+(1-α)ρk1,其中α表示0-1离散均匀分布的随机变量。本文中选取交叉概率pc=0.8。
③变异:对种群中每个个体以变异概率pm随机改变某一基因位的值。本文设定变异概率pm=0.6。
本文借助MATLAB软件进行编程实现此算法,主要步骤为:
Step 1 采用实数编码,构造符合约束条件的染色体,并将种群规模设为100;
Step 2 计算个体的适应度,选择适应度最大的个体;
Step 3 按照交叉概率进行交叉操作;
Step 4 按照变异概率进行变异操作;
Step 5 设定最大迭代次数G=500,如达到500代时算法结束,输出求解结果,如未达到,返回Step 2。
3 仿真实验
假设有六种组分油进入产品调和装置,生产出3种成品油:90#汽油、93#汽油和柴油。实例中成品油的质量指标参数如表1所示:

表1 油品质量指标参数
参数设计:
应用本文采用的遗传算法进行计算,具体设计如下:采用实数编码,种群的大小设为100,进化代数设为500,参数设置如下:T=7,pc=0.8,pm=0.6。选择方法为轮转法,停止的方法设为达到最大进化次数,对比实验设计如下:
(1)组分油的单位采购/生产成本Pit在(1000,1500)内随机产生,最大使用量maxit在(18000,20000)内随机产生;
(2)成品油的需求量Dkt在(3000,5000)内随机产生;
(3)油品的最大存储能力Vi限制在(200000,300000)内随机产生;
(4)单位烯烃环保成本cosk在(100,150)内随机产生;
(5)装置的最大生产能力Capt限制在(400000,500000)内随机产生;
(6)组分油和成品油的单位库存成本hi在(50,100)内随机产生:
①第一组实验中使组分油和成品油的单位启动成本si在(10000,15000)内随机产生;
②第二组实验中使组分油和成品油的单位启动成本si在(15000,20000)内随机产生;
③第三组实验中使组分油和成品油的单位启动成本si在(20000,25000)内随机产生;
(7) 组分油和成品油的单位启动成本sit在(15000,20000)内随机生产:
①第一组实验中使组分油和成品油的单位库存成本hi在(1,50)内随机产生;
②第二组数据中使组分油和成品油的单位库存成本hi的(50,100)内随机产生;
③第三组数据中使组分油和成品油的单位库存成本hi的(100,150)内随机产生。
实验分为两组,每组实验数据运行七次,其运算结果如表2和表3所示:
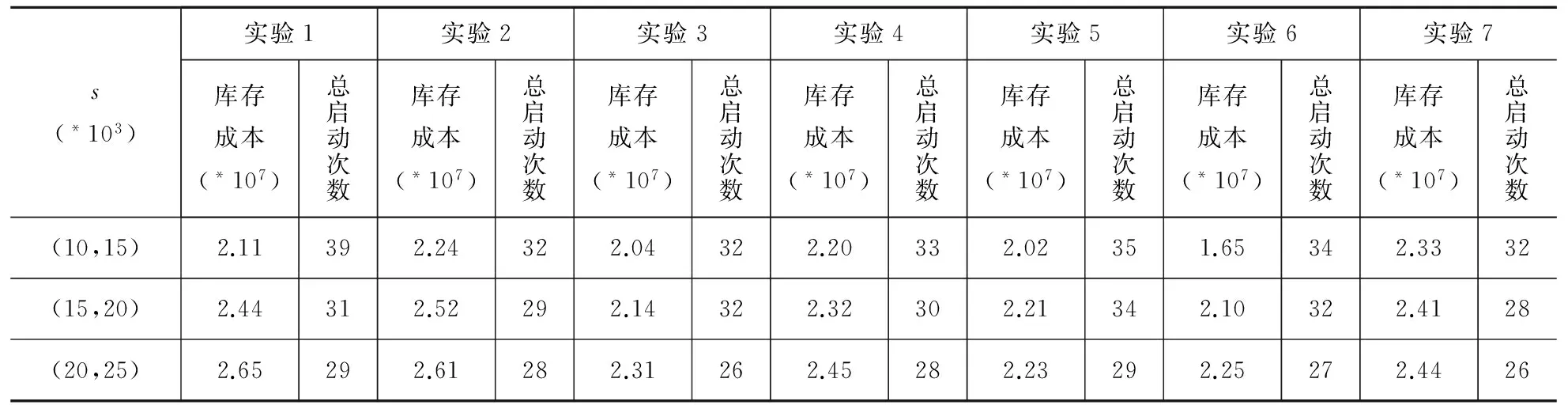
表2 计算结果对比分析表(当单位库存成本不变,单位启动成本逐渐增大时)

表3 计算结果对比分析表(当单位启动成本不变,单位库存成本逐渐增大时)
由上述计算结果不难看出:
(1)当单位库存成本不变,单位启动成本逐渐增大时,库存总成本随之增加,总启动次数随之减少。这是因为在单位启动成本逐渐增大的过程中,相同启动次数对应的启动成本随之增加,因此当单位库存成本给定时,成品油调和配方优化过程倾向于通过增加库存量,减少总启动次数,实现降低生产总成本的目的。
(2)当单位启动成本不变,单位库存成本逐渐增大时,总启动次数随之增加,库存总成本随之减小。这是由于当单位库存成本逐渐增大时,库存总成本对生产总成本的影响随之增加,因此当单位启动成本给定时,成品油调和配方优化过程倾向于通过增加总启动次数,减少库存量来降低企业的生产成本,从而达到提高企业经济效益的目的。
4 结论
本文以最小化企业生产总成本为目标,在需求确定的情况下,针对成品油调和配方优化问题进行了研究,建立了相应的混合整数规划模型,并利用遗传算法对其进行了求解。通过对计算结果的对比分析可以看出,在成品油调和配方优化的过程中充分考虑了库存成本与启动成本的联合优化,从而最大程度地降低了企业的生产总成本,最终实现了最大化企业利益的目的。
[1] Nelson W L. Predict research octane number for gasoline blends[J]. Oil and Gas, 1955, 54 (20): 135-138.
[2] Glismann K, Gruhn G. Short-term planning of blending processes: scheduling and nonlinear optimization of recipes[J]. Chemical Engineering & Technology, 2001, 24(3): 246-249.
[3] Jia Z Y, Ierapetritou M. Mixed-integer linear programming model for gasoline blending and distribution scheduling[J]. Industrial & Engineering Chemistry Research, 2003, 42(4): 825-835.
[4] 李响.油品调和优化问题的研究[D].大连理工硕士学位论文,2010.
[5] 罗春鹏,荣冈.不确定条件下汽油调和调度的鲁棒优化模型[J].石油学报(石油加工),2009,25(3):391- 400.
[6] 江永亨,蔡阳阳,黄德先.无主炼原油的原油调和调度问题[J].化工学报,2010,61(8):2015-2020.
[7] 马义飞,孙晓燕.成品油二次配送调度优化模型及其遗传算法求解 [J].运筹与管理, 2010,19(6): 73-78.
[8] 崔承刚,吴铁军.基于活跃约束条件辅助目标的进化算法求解油品调合问题[J].化工学报,2010,61(11):2881-2888.
Research on the Optimization of the Recipe for Product Oil Blending
LIU Guo-li1, YE Tong1, WANG Gui-ling1, ZHAO Jun2
(1.SchoolofScience,UniversityofScienceandTechnologyofLiaoning,Anshan114051,China; 2.ResearchCenterofInformationandControl,DalianUniversityofTechnology,Dalian116024,China)
Product oil blending is an important step for oil refining, which directly affects the economic benefits of oil refineries. Using petrochemical industry as background, this paper does a research on the optimization of the recipe for product oil blending. A mixed-integer programming model is developed to minimize the total production cost of the refinery on the condition that product quality indexes are satisfied, and an efficient solving strategy based on genetic algorithm is proposed. Then a simulation experiment is made according to the actual production data of an oil refinery and the balance relationship between the inventory cost and the setup cost is showed by computational results. To be specific, the total inventory cost increases and the number of setups decreases, when the unit inventory cost remaines constant and the unit setup cost increases. Conversely, the number of setups increases and the total inventory cost decreases, when the unit setup cost remaines constant and the unit inventory cost increases.
product oil blending; production-inventory planning; genetic algorithm; refinery industry
2012-12-10
国家自然科学基金资助项目(61034003);国家青年基金(71301066);辽宁省教育厅科学研究一般项目(L2013120);辽宁科技大学优秀科技人才基金(2012RC03);辽宁科技大学国家级项目预研项目(2012YY14)
刘国莉(1978-),女,博士后,副教授,硕士导师,主要从事工业过程优化建模、生产库存管理、供应链协调、最优化算法等方向的研究。
F273 TE624
A
1007-3221(2015)04- 0092- 05

