基于市场需求增加的双渠道闭环供应链定价机制研究
李向荣, 张克勇
(中北大学 经济与管理学院,山西 太原 030051)
基于市场需求增加的双渠道闭环供应链定价机制研究
李向荣, 张克勇
(中北大学 经济与管理学院,山西 太原 030051)
针对制造商开辟在线销售渠道现象的普及,考虑混合双渠道销售会增加产品的潜在需求,构建制造商与零售商分散、集中定价两种决策模型,利用博弈理论对模型进行求解分析,研究表明在双方分散、集中两种定价策略模型中,随着双渠道开通导致的市场需求率的增加,制造商的批发价、零售商的销售价格上调,零售商的回收价格下降,闭环供应链系统总利润则呈现先下降后上升的变化。最后,运用数值算例进一步验证和讨论双渠道销售导致的市场需求增加对闭环供应链系统定价策略、双方利润及系统渠道效率的影响。
市场需求增加;制造商双渠道;闭环供应链;定价
0 引言
进入21世纪以来,随着社会的进步和科学技术的发展,产品的使用周期缩短,更新换代速度加快,导致社会上废旧产品存储量快速积累。在资源危机和环境污染的双重压力下,废旧产品的逆向物流受到了政府、企业和学者等各界越来越多的关注。基于此现状及发展趋势,闭环供应链管理的相关研究得到重视。近年来,伴随着目前互联网的逐渐成熟和广泛运用,我国电子商务正在快速发展,越来越多的制造商建立其在线直销渠道以促进企业自身快速发展,并且逐渐成为市场交易过程的重要组成部分。制造商增设在线销售渠道对供应链中零售商以及制造商自身而言既是一种挑战也是一种机遇。本文将围绕制造商开辟在线直销渠道后闭环供应链中定价策略以及利润状况进行研究,为现实中企业开辟在线渠道提供一些决策依据。
关于闭环供应链系统决策与优化问题已有许多相关的研究。Liang Y J等[1]研究了闭环供应链中制造商的定价策略,但没有考虑闭环供应链中零售商等其他节点对制造商制定价格决策的影响。顾巧论等[2]探讨了闭环供应链中逆向物流的定价决策问题,但没有涉及正向物流对逆向物流决策的影响作用。易余胤[3]、Onur K[4]考虑了闭环供应链中各个节点制定价格的策略方式,分别对分散化、协调定价决策进行了分析与验证。Shi J M等[5,6]、Chen J M 等[7]分别从需求、回收随机化以及新旧产品渠道竟争等不同方面建立数学模型,研究了闭环供应链各节点的定价与协调问题,但没有考虑双渠道销售情形下的定价策略。张克勇等[8]、熊中楷等[9]、王玉燕[10]分别研究了基于零售商竞争、经销商从事再造过程以及政府干预等视角下,闭环供应链的定价策略及系统效率问题,但文献未涉及正向物流双渠道或者逆向物流双渠道情形。颜永新等[11]建模分析了销售商和制造商开辟在线渠道两种情形下的决策和收益,并设计了供应链系统协调机制实现了供应链协调和系统效率优化,但研究的是基于制造商Stackelberg博弈的供应链模型。许传永[12]通过对制造商和零售商分别采取单渠道和双渠道情况进行比较分析,研究表明制造商开辟双渠道对其自身收益是有利的,但考虑的是正向物流供应链,并没有考虑逆向物流可能对供应链中决策产生影响。易余胤等[13]构建了双渠道冲突条件下闭环供应链决策模型,分析分散决策以及联合定价决策下各个价格的制定策略,分析了销售渠道冲突和回收渠道冲突对制造商、零售商定价决策和利润的影响,但文献只是探讨双渠道下的定价策略及利润,并没有考虑到制造商双渠道或者零售商双渠道均会带来市场需求量的增加。陈军等[14]探讨了零售商主动开辟外部二级市场环境下供应链系统双方最优定价决策与利润,研究表明零售商开辟二级市场能够提升供应链系统绩效。黄松等[15]、曹二保等[16]均研究了市场需求和成本扰动时双渠道供应链系统决策、收益和协调问题。赵礼强等[17]研究了制造商采取混合渠道所导致的冲突及协调问题,研究发现制造商通过设计改进的收入共享契约可以同时解决双渠道冲突与协调,但文献都没有考虑回收问题,只是传统开环供应链中的研究。于春梅等[18]研究了存在双渠道回收的闭环供应链系统定价与协调问题,结果表明闭环供应链采取双渠道回收模式对系统各方收益和整个闭环供应链再制造系统的效率都是有利的。林杰等[19]则研究了闭环供应链系统中销售与回收均采取双渠道时供应链成员的定价决策与收益问题,但文章并未涉及开辟在线渠道所引起的市场需求增加及其影响问题。
综上所述,已有研究大多集中于单一渠道的定价策略,然而在现实中广泛存在着制造商或者零售商开辟在线渠道的现象,即使有少量的研究文献考虑了双渠道问题,但没有考虑这种混合渠道所带来的市场需求增加的变化及其影响问题。
本文研究有别于以往的研究文献,将在闭环供应链背景下,考虑制造商开辟在线销售渠道会增加产品的潜在市场需求量。构建基于市场需求增加的闭环供应链系统决策模型,分析制造商开辟在线销售渠道所带来的市场需求量增加率对供应链系统各方最优定价决策和利润的影响,以及这种在线销售渠道的开辟对废旧产品的回收及其供应链系统利润的影响。
1 问题描述与模型假设
1.1 问题描述
本文研究背景为单一制造商和单一零售商构成的闭环供应链系统,见下图1。在该闭环供应链系统中,制造商一方面通过零售商的销售渠道进行产品销售,另一方制造商自己开辟第二在线销售渠道进行直销。根据文献[20][21],在再制造闭环供应链中,若制造商自行回收,供应链效率是比较低的,因此本文考虑闭环供应链中仅采用一种回收渠道:零售商先向消费者回收废旧产品,进而制造商再从零售商处回购进行再造。
在本文的闭环供应链模型中,将考虑分散化决策下的模型与集中化决策下的模型在定价策略的不同。在本文中下标“M”表示制造商,“R”表示零售商,“T”表示供应链系统,i=1表示在分散化决策下的模型中,i=2表示在集中化决策下的模型中;上标“*”表示最优,“’”表示在集中定价策略模型中。考虑到回收的产品在再制造的过程中与新产品的单位生产费用存在差异,通常我们把采用全新材料制造的产品称为“新产品”,用cM表示单位成本,而使用回收废旧品进行再制造的产品称为“再造品”,用cR来表示单位成本。显然,cM>cR。

图1 双销售渠道下闭环供应链系统结构模型
1.2 模型假设
本文基于所研究的问题做以下合乎经济学规律的逻辑假设:
假设1:制造商生产的新产品和再造品在质量和功能上完全一致,两种产品在市场上的销售价格相同,即在整个销售过程中,销售的都是一种同质无差异的产品。
假设2:本文参照文献[22]的做法,根据价格敏感的市场需求函数形式,令
在线渠道中,制造商的销售量为:QM=(θ+ρ)·b0-b1·pM+b2·pR
传统渠道中,零售商的销售量为:QR=(1-θ)·b0-b1·pR+b2·pM
其中,θ表示双渠道下在线渠道销售者需求的市场份额;ρ表示制造商引入在线销售渠道之后,市场中增加的产品需求率,考虑现实因素,一般增加的市场需求量不会成倍增长,故假设0<ρ<1,同时新增的产品需求量都由制造商直接在线供给;b0表示市场基准需求量(b0>0);b1表示双渠道下价格需求弹性;b2表示在线渠道和传统渠道的替代率,由销售服务等因素决定(b1>b2>0);pM表示制造商通过在线渠道销售给消费者的产品价格;pR表示零售商通过传统渠道销售产品的产品价格。
假设3:假设制造商开通在线渠道后,产品的市场需求量和废旧产品回收量都会增加,所增加的部分回收量主要体现在基本回收量上,本文在参考相关文献关于废旧品回收量函数的基础上,给出零售商的废旧产品回收量函数为:
DR=ρ·l0+l1·aR
上式中的l0代表废旧品的基本回收量(l0>0);l1代表废旧品回收价格对回收量的影响程度,aR代表废旧品的市场回收价格。
假设4:假设制造商在竞争市场上占据主导地位,零售商为市场跟随者,两者之间为Stackelberg序贯博弈,双方对对方的决策行为信息是完全和充分的,制造商根据零售商的价格决策来做出其自身最优价格策略,双方为完全理性的决策者,均以自身利润最大化作为决策的目标。
2 模型构建及分析
2.1 分散化决策下的双渠道闭环供应链模型
在分散化决策定价策略的双渠道闭环供应链模型中,制造商的利润函数πM与零售商的利润函数πR分别为:
πM=(w-cM)·QR+(pM-cM)·QM+(cM-cR)·DR-aMR·DR
(1)
πR=(pR-w)·QR+(aMR-aR)·DR
(2)
根据逆向归纳法,第一阶段,零售商以最大化自己利润为目标,制定批发价格。先求零售商的反应函数
令R1(pR)=0,R2(aR)=0,得
(3)
(4)
将式子(3)(4)带入式子(1)中,并联立如下方程组:
解得
将结果代入式子中,得到
将求得的所有最优解代入利润函数式子(1)(2)中,得
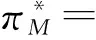
结论1 在分散化决策下,批发价格、销售价格均随制造商开辟在线渠道后增加的市场需求率ρ的增加而上升。
证明:将各销售价格对ρ求一阶导数,易知
即随着增加的市场需求率ρ的增大,分散决策下批发价格w、销售价格pM、pR均上升。
管理启示:结论1表明在制造商开通在线渠道的初期,消费者对这种购买渠道可能不适应,这时候制造商和零售商往往会通过低价来刺激和吸引消费者购买,在集聚相当的消费者后,随着消费者需求的逐渐增多,产品的销售状况越来越好,则批发价格会越来越高,相应的,产品的销售价格也会调高。这告诉我们企业开辟在线渠道初期进行大量的宣传和建设投入是可行的,当在线渠道引起市场需求增加时,制造商和零售商都可以通过提升产品的批发价格和销售价格来获取更多的收益。
结论2 在分散化决策下,回收价格均随制造商开辟在线渠道后增加的市场需求率ρ的增加而降低。
证明 易知
即分散决策下零售商、制造商的回收价格aR、aMR是关于市场需求增加率ρ的减函数。
本文假设的是所有废旧产品均由零售商代为回收,制造商再从零售商处回收。由于开通在线渠道后,产品的宣传力度增大,市场需求总量增加,相应的,废旧产品产生量增加。一般地,随着市场中废旧产品产生量越多,逆向物流中产品的回收价格越低。
管理启示:结论2告诉我们制造商开辟在线渠道会使得市场产品需求增加,从而返回的废旧产品也就越多,此时制造商和零售商则会降低其各自的回收价格从而获取更多的市场收益,即努力开辟在线渠道对供应链双方的回收都是有利的。
结论3 在分散化定价模型中,随着市场需求量的增加,制造商在线渠道销售量与产品回收量逐渐增加,而零售商的销售量没有显著增加。
证明:在分散化定价模型中,即制造商主导的Stackelberg博弈定价策略下,由于
在本文中,假设增加的市场需求均由制造商在线渠道供给,根据结论3,分散定价决策下零售商的销量与增加的市场需求量无关。
结论4 非合作博弈下,零售商的利润与市场增加需求率ρ呈正相关关系;而制造商的利润则为市场增加需求率的严格凹函数。
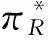
这表明制造商的利润曲线是关于参数ρ的严格凹函数,且存在一个临界值:
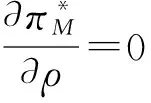


管理启示:结论4表明,制造商通过大量的市场宣传来开辟在线销售渠道使得其总的市场销售量增加。而随着市场的需求量增加,零售商则会提高产品市场销售价格,降低其废旧产品的市场回收价格,双重作用使得零售商的利润不断上升。而作为闭环供应链主导者的制造商,在开辟在线渠道初期,其投入的费用远高于增加的批发、销售价格以及降低废旧品回收价格所带来的收益,然而随着产品市场需求量的不断增长,处于市场主导地位的制造商收益也会随之不断增加,所以在Stackelberg博弈定价模型中,随着市场增加需求量的增大,制造商的利润先降低,后上升。这告诉我们在实践中,零售商应该鼓励制造商进行在线渠道的开辟,共同加大产品的市场宣传力度,并给予制造商开辟在线渠道一些支持,这样就可以从需求增加中获取更多的收益。
2.2 集中化决策下的闭环供应链模型
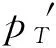

图2 集中化决策下闭环供应链模型
在集中化决策模型中,对于制造商与零售商组成的系统而言,总收入为产品销售收益与利用回收产品再造所节省的费用之和,总支出为废旧品回收过程中支付给消费者的回收费用,因此,系统利润函数为:
求解,得到最优解
代入利润函数,得
结论5 在制造商与零售商联合制定价格策略方式下,系统销售价格随制造商开辟在线渠道后增加的市场需求率ρ的增加而上升;回收价格随制造商开辟在线渠道后增加的市场需求率ρ的增加而下降。
证明 将销售价格、回收价格对ρ求一阶导数,易知

结论6 在合作集中决策中,闭环供应链系统的销售量和废旧品回收量均与市场需求量呈正相关关系;且集中化定价策略下的废旧产品回收量总大于分散定价策略下的回收量。
证明在制造商与零售商联合定价模型中,由于
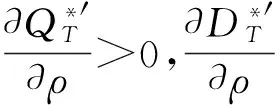
对于不同策略的定价模式,其系统的废旧产品回收量有
即集中定价策略下的回收量总大于分散定价策略下的回收量。
根据结论3,集中化定价策略可以增加废旧产品的回收量,对环境保护有更大的效益。
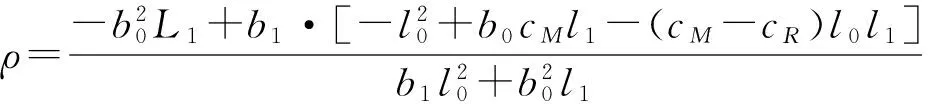


管理启示:在集中定价模型中,制造商进行在线渠道开辟的前期,需要投入大量的宣传费用和相关建设费用,而前期这种在线渠道所引起的市场需求增加量较少,即市场需求增加量所获取的收益要小于宣传和建设费用的投入,因此制造商与零售商组成的系统利润将会降低,随着消费者对这种在线消费的接受程度增加,市场需求量的不断增加,系统利润经过利润函数曲线的最低拐点后不断上升。这告诉我们制造商进行在线渠道的开辟来增加市场需求量也是存在一定风险的,只有通过投入使得市场需求率增加高于某个临界点时,供应链系统利润才会增加,否则就会使得系统利润减少,因此制造商在开辟在线渠道前要对这种投入引起的市场需求增加率进行预测。
3 数值仿真分析
为了对本文所得结论进行验证及更深入的探讨,下面进一步进行数值仿真分析。假设制造商与零售商销售量函数中有关参数为b0=200,b1=4,b2=2;零售商回收量函数中l0=10,l1=20;制造商制造全新产品的制造费用cM=10,采用废旧品再制造的费用cR=4;双渠道销售策略下,在线销售渠道在市场总销售量所占的市场份额θ=0.3。
3.1 增加的市场需求率对价格的影响
根据假设的参数赋值,首先对分散、集中两种决策方式下增加的市场需求率对销售价格以及回收价格的影响进行数值仿真,结果如图3、图4所示。
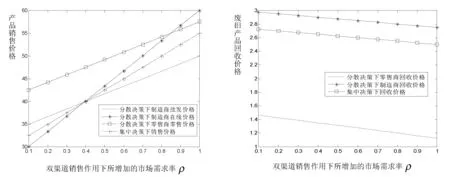
图3 增加的市场需求率对各销售价格的影响 图4 增加的市场需求率对废旧产品回收价格的影响
由图3和图4可以看出:
(1)当销售渠道由原来的单一传统零售商销售渠道变为双渠道后,由于增加了制造商在线销售渠道,相当于增大了产品的宣传力度,导致产品的市场需求增加。由图3,不论制造商与零售商分散定价或者集中制定价格策略,随着市场需求的增加,制造商与零售商的销售价格都会有不同程度的提高,这是由于产品的市场需求增大,销售状况变得越来越好,制造商与零售商会适当调高需求产品的销售价格来增加自身的利益。此仿真结果与结论1、结论5相吻合。
(2)由图4,当增加制造商在线销售渠道后,不管制造商与零售商分散决策还是集中决策,随着市场需求量的增加,导致市场中废旧产品的产量也越来越多,这就意味着回收过程中零售商回收价格会有所降低。由于本文假设的是分散决策下废旧产品的逆向物流渠道是唯一的,仅由零售商负责从消费者手中回收,制造商则再从零售商处以较高的价格获取废旧产品。而对于消费者而言,分散决策下废旧品的回收价格要较集中决策时略低些,对于消费者是更有利的。这也与结论2与结论5中相关分析相符合。
3.2 增加的市场需求率对销售量、回收量的影响
其次,对分散、集中两种决策定价方式下增加的市场需求率对产品的销售量以及回收量的影响进行数值仿真,变化趋势图如图5、图6所示。 由图5和图6可以看出,当增加制造商在线销售渠道之后,随着市场需求量的增加,产品的销售量及回收量都相应增加。需要指出的是,本文假设增加的市场需求全部由制造商在线供应,因此分散定价决策下,零售商的销售量并没有增加。产品的市场需求增大,销售量相应增大,导致市场中废旧产品产生量增加,那么回收量也会增加。仿真结果与模型分析中结论3与结论6相关陈述相吻合。由图6可以明显看出,集中决策时废旧产品的回收量较大,考虑到废旧产品的回收可以带来经济与环境的双赢,因此,制造商与零售商进行集中定价是非常有必要的。

图5 增加的市场需求率对产品销售量的影响 图6 增加的市场需求率对废旧产品回收量的影响
3.3 增加的市场需求率对利润的影响
接下来,对分散、集中两种决策定价方式下增加的市场需求率对制造商、零售商利润的影响进行数值仿真,结果如图7所示。

图7 增加的市场需求率对零售商、制造商利润的影响 图8 增加的市场需求率对系统效率的影响
由图7可以看出,分散决策定价方式下,当销售渠道变为双渠道时,随着市场需求的增加,制造商的利润有了很大幅度的提高,这是源于所假设的增加的市场需求均由制造商在线直接供给;而零售商的利润几乎不变。这与结论4似乎不太相符,实际上,零售商的利润是有所增加的,只是幅度偏小,在利润整体趋势上几乎微乎其微。同时,变化趋势图中制造商利润并没有像结论4中所说先下降再上升,这是由于理论趋势图中的临界点(拐点)位于竖轴的左边,现实生活中增加的市场需求率是绝对大于零的,因此,实际上制造商的利润是随着市场需求的增加而上升的。同理,集中决策定价方式下的制造商与零售商系统利润在现实生活中也是增加的,并且由图可知,分散决策下闭环供应链系统收益要小于集中决策的情形。
3.4 增加的市场需求率对系统效率的影响
由于本文主要研究增加制造商在线销售渠道后,不同决策方式下增加的市场需求量对各个价格以及利润的影响,因此,引入系统效率的计算,系统效率的计算公式如下:
将增加的市场需求率ρ对系统效率的影响进行数值仿真,变化趋势图如图8所示。
由图8可知,开辟在线渠道增加市场需求量会有效提高整个闭环供应链系统效率。这是由于随着双渠道销售模式的深入,市场需求逐渐增大,导致分散决策定价方式下制造商的利润得到迅速提高,并且增长幅度远大于集中决策定价策略下的系统利润,因此,闭环供应链的运作效率有所改善。同时,由图8可以看出,集中定价总利润总大于分散定价总利润,且当双渠道销售带来市场需求翻倍的效果时,系统效率为1,即分散决策下制造商与零售商的总利润与集中决策方式下系统利润相同。因此,若供应链系统成员能够合作进行定价决策,这对于整个供应链系统的运作效率提升是非常有效的。
4 结语
本文建立了单一制造商与单一零售商组成的闭环供应链模型,考虑增加制造商在线销售渠道后会导致市场需求增加,研究了增加的市场需求对零售商与制造商定价及利润的影响,并根据制造商与零售商分散定价策略、集中定价策略情形进行了对比分析。研究表明,分散决策下,制造商的产品批发价、在线销售价格和零售商的产品销售价格与市场需求增加量呈显著的正相关关系,而废旧产品回收价格则与市场需求增加量呈负相关关系,同时制造商在线渠道销售量与产品回收量随市场需求量的增加而逐渐增加,零售商的销售量则没有显著变化,制造商的收益在过临界点后快速提高,但零售商的收益增加的幅度微乎其微;集中定价策略下,随着在线销售渠道开辟所引起的市场需求的不断增加,零售商和制造商的系统销售价格上升,回收价格下降,系统销售量与回收量均逐渐增加,系统利润在到达某一个临界点之后也逐渐增加。最后,本文运用数值算例,分析了不同定价策略下双渠道销售带来的市场需求增加对供应链系统成员定价策略和收益的影响,探讨此时闭环供应链系统运作效率的变化趋势,验证和补充了前面的理论成果。
本文研究了制造商双渠道销售模式下会增加产品的市场需求,为企业的现代化管理提供了一定的理论基础。但结论还可进一步扩展,比如零售商与制造商的在线双渠道销售同时存在的情况,以及废旧产品的回收并不全权由零售商负责的情况等等,并且,本文只验证了制造商与零售商集中制定价格策略是更有效的,没有涉及到集中定价的利润分配问题,即如何制定契约优化供应链运作效率,这些都是值得今后进一步研究的方向。
[1] Liang Y J, Pokharel S, Lim G H. Pricing used products for remanufacturing [J]. European Journal of Operational Research, 2009, 193: 390-395.
[2] 顾巧论,高铁杠,石连栓.基于博弈论的逆向供应链定价策略分析[J].系统工程理论与实践,2005,(3):20-25.
[3] 易余胤.具竞争零售商的再制造闭环供应链模型研究[J].管理科学学报,2009,12(6):45 -54.
[4] Onur K. Incentive and production decisions for remanufacturing operations[J]. European Journal of Operational Research, 2010,201: 442- 453.
[5] Shi J M, Zhang G Q, Sha J C. Coordinating production and recycling decisions with stochastic; demand and return[J]. Journal of Systems Science and Systems Engineering, 2010, 19(4): 385-407.
[6] Shi J M, Zhang G Q, Sha J C. Optimal production planning for a multi-product closed loop system with uncertain demand and return[J].Computer & Operations Research,2011,38(3): 641- 650.
[7] Chen J M, Chang C. The competitive strategy of a closed-loop supply chain with remanufacturing[J]. Transportation Research Part E, 2012, (48) :387-400.
[8] 张克勇,周国华.零售商竞争环境下闭环供应链的协调问题研究[J].技术经济,2008,27 (10) :114-118.
[9] 熊中楷,王凯,熊榆.经销商从事再制造的闭环供应链模式研究[J].管理科学学报,2011,14(11) :1-9.
[10] 王玉燕.政府干涉下双渠道回收的闭环供应链模型分析[J].运筹与管理,2012,21 (3):250-255.
[11] 颜永新, 徐晓燕. 零售商双渠道适应性及协调研究[J].系统管理学报, 2012, 21(5): 603-608.
[12] 许传永. 两层双渠道供应链的优化与协调若干问题研究[D].合肥:中国科学技术大学,2009.
[13] 易余胤,袁江.渠道冲突环境下的闭环供应链协调定价模型[J].管理科学学报,2012, 15(1):54-65.
[14] 陈军,赖信,许茂增,吴庆.零售商开辟二级市场下双渠道供应链定价决策[J].系统工程学报,2013,28(6):786-794.
[15] 黄松,杨超,杨珺.需求和成本同时扰动下双渠道供应链定价与生产决策[J].系统工程理论与实践,2014,34(5):1219-1229.
[16] 曹二保,郑健哲,马玉洁,赖明勇.双渠道供应链应对需求扰动的协调机制研究[J].管理学报,2014,11(2):267-273.
[17] 赵礼强,徐家旺.基于电子市场的供应链双渠道冲突与协调的契约设计[J].中国管理科学,2014,22(5):61-68.
[18] 于春海,李想.闭环供应链双渠道回收系统定价机制与协调策略[J].东北大学学报(自然科学版)2014,35(9):1360-1368.
[19] 林杰,曹凯.双渠道竞争环境下的闭环供应链定价模型[J].系统工程理论与实践,2014,34(6):1416-1424.
[20] Savaskan R C,Bhanttacharya S, Van Wassenhove L N. Closed-loop supply chain models with product remanufacturing [J].Management Science, 2004, 50(2): 239-252.
[21] 洪宪培,张怀阁,王德志.双渠道销售和回收情况下闭环供应链模型研究[J].统计与决策,2012,20:50-54.
[22] 李书娟,张子刚,黄洋.风险规避对双渠道供应链运作模式的影响研究[J].工业工程与管理,2011,16(1):32-36.
Pricing Mechanism Based on Market Demand Increases in the Dual-Channel Closed-loop Supply Chain
LI Xiang-rong , ZHANG Ke-yong
(SchoolofEconomicsandManagement,NorthUniversityofChina,Taiyuan030051,China)
According to the popularity of the phenomenon that more and more manufacturers are opening up online sales channels, the paper constructs the models that the manufacturer and retailer price in decentralized or centralized decision, considering the potential demand from the double channel sales. And then the paper solves and analyzes the models by using the game theory. The study shows that the manufacturer’s wholesale, retailer’s sales prices increase and recycling prices decline with the increasing rate of demand, and at the same time the total supply chain profit decreases firstly and then increases in both models. Finally, the paper verifies and discusses the influence that increases market demand from the double channel sales on the pricing strategy, profits and channel efficiency in closed-loop supply chain by using the numerical examples, and additionally it finds that the potential demand from the double channel sales has a significant positive impact on the efficiency of the closed-loop supply chain.
market demand increasing; double-channel of manufacturer; closed loop supply chain; pricing
2014- 08- 07
教育部青年基金资助项目(13YJC630049);山西省哲学社会科学规划课题(SXZXSKGHKT2013018);山西省社科联重点课题研究项目(SSKLZDKT2013060)
李向荣(1976-),男,博士,中北大学经济与管理学院讲师,硕士生导师,研究方向为供应链管理与公司治理;张克勇(1972-),男,博士,中北大学经济与管理学院教授,硕士生导师,研究方向为闭环供应链管理。
C931
A
1007-3221(2015)04- 0058-10

