灰色实物型投入产出分析的覆盖解研究
李桥兴, 刘思峰
(1.贵州大学 管理学院,贵州 贵阳 550025; 2.兰州理工大学 经济管理学院,甘肃 兰州 730050; 3.南京航空航天大学 经济与管理学院,江苏 南京 210016)
灰色实物型投入产出分析的覆盖解研究
李桥兴1~3, 刘思峰3
(1.贵州大学 管理学院,贵州 贵阳 550025; 2.兰州理工大学 经济管理学院,甘肃 兰州 730050; 3.南京航空航天大学 经济与管理学院,江苏 南京 210016)
由于国民经济系统的复杂性,人们在使用实物型投入产出分析工具时不可能获得各部门产品的投入与产出的确定值。采用灰色系统理论基本原理提出灰色实物型投入产出分析并给出模型及各种灰色分析系数的覆盖解公式。灰色实物型投入产出分析能处理统计数据为区间的情形,可以使决策者在不确定性情况下对复杂经济系统进行分析、预测和控制,提高人们的抗风险能力。模拟案例验证了模型计算的可行性。
数量经济学;灰色实物型投入产出分析;灰色覆盖运算;复杂经济系统;灰色系数
0 引言
实物型投入产出分析是以实物为计量单位、反映一个国家的国民经济在某个时期内投入与产出间数量关系的经济模型,包括投入产出表、投入产出模型及应用,已经在许多领域得到成功应用[1~5]。灰色系统理论以具有贫信息特征的客观事物内涵的认知过程为研究对象,通过加工已知信息达到管理和控制系统发展的目的[6~9]。灰色数学包括灰数运算、覆盖运算、唯一潜真运算和白化运算等形式,是一种新型不确定数学运算[10~12]。灰数是一种来源于信息缺失的不确定数。由于信息的缺失,人们无法得到它的真实值。但是在正确的调查统计手段下,人们可以得到一个数值范围,并使不确定数的真实值落在范围之内。这个数值范围称为灰数的覆盖集,其内任意一个实数称为灰数的白化数。不知道确切取值的数值称为灰数的唯一潜真值[10,11]。灰数的覆盖集可能是连续也可能是离散的,连续的覆盖集用区间表达。当所有的信息都出现时,覆盖集会演变成只包含一个数的集合,灰数变成一个确定的实数[10,11]。区间数与区间覆盖集除了有相似的计算形式外,它们之间有很大的区别。区间覆盖集是灰色朦胧集。有关灰数的详细讨论及区间数和区间覆盖集的差异,读者可参考文献[10~13]等。
在现实中用投入产出分析去预测和管理国民经济时,我们往往要求统计数据是精确的。然而,复杂经济系统受很多因素如技术条件、管理水平、原材料可得性、国家政策等的影响,使我们很难收集足够的信息去得到统计数据的准确值,因此决策时会丢失很多有用的信息。但是通过采用正确的调查统计方法,我们可以得到一个包含准确值的覆盖集。不失一般性,这个覆盖集可以用区间表示。文献[14~18]分别提出灰色价值型投入产出分析、灰色动态投入产出分析、灰色非线性投入产出分析、灰色投入占用产出分析、灰色部门投入产出分析、灰色企业投入产出分析和灰色地区投入产出分析。本文在前文基础上,提出灰色实物型投入产出分析并给出覆盖解公式,同时用一个模拟案例说明结论的可行性。
1 灰色实物型投入产出分析
本文假定读者已经具备实物型投入产出分析的基本知识,也可以参阅文献[1]等。
国民经济系统是一个巨大而复杂的系统。由于信息不充分导致无法获取各部门的投入和产出的精确数据,因而实物型投入产出分析中的数据表现为灰数。在正确的调查统计方法下,我们可以得到每个灰数的区间覆盖集。于是得到灰色实物型投入产出如表1。

表1 灰色实物型投入产出表
表1中变量的含义如下:
qij(⊗):第j个部门投入到第i部门的灰色中间投入实物量或第i个部门供给第j个部门的灰色中间产出实物量(i=1,…,n;j=1,…,n,n+1,…,n+l)。请注意在I栏中的 qij(⊗)(j=1,2,…,n)是列名产品之间的中间产出/中间投入,在II栏中的是qij(⊗)(j=n+1,…,n+l )未列名产品和列名产品之间的中间产出/中间投入。未列名产品是指这样的一些生产部门如交通运输业、建筑业、商业和餐饮业等,这些部门只参与产品的生产过程但是不生产具体的产品。未列名产品对实物型投入产出分析很重要。如果不考虑他们,模型将失去平衡。
yi(⊗):由第i(i=1,…,n)个部门生产的最终使用价值灰色实物量。最终使用是本时期内没有进入生产过程的那部分产品。根据应用领域不同,最终使用可以分为几部分,如固定资产更新改造、基础设施、居民消费、集体消费、非物质部门生产包括运输业、商业、餐饮业及存货和出口商品等。
wi(⊗):从国外进口的产品i(i=1,…,n)的灰色实物量。
Qi(⊗):由第i(i=1,…,n)个部门生产的总产出灰色实物量。
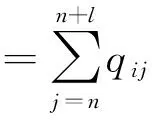
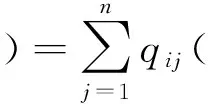
(1)
在正确的调查方法下,我们得到灰数qij(⊗),yj(⊗),wi(⊗)的区间覆盖集分别为

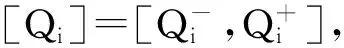
(2)

根据文献[1,8],我们得到以下实物型投入产出分析方法的各种灰色系数及其覆盖集。
1.1 灰色直接消耗系数aij(⊗)及其覆盖集[aij]
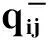
(3)
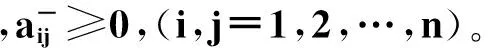
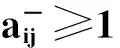
A(⊗)=(aij(⊗))n×n称为灰色直接消耗系数矩阵,[A]=([aij])n×n为A(⊗)矩阵覆盖集。
灰色直接消耗系数反映了在不确定情况下的经济活动期间各列名产品之间的数量依存关系,它的覆盖集反映了这种数量关系的大概范围。在贫信息状态下,灰色直接消耗系数对分析、预测和控制复杂经济系统具有重要作用,可以大大减少调查成本。
1.2 灰色完全消耗系数
设bij(⊗)(i,j=1,…,n)为灰色完全消耗系数,B(⊗)=(bij(⊗))n×n为灰色完全消耗系数矩阵,则由文献[1]等,有B(⊗)=A(⊗)+B(⊗)A(⊗)。显然。如果I-A(⊗)是非奇异矩阵,则它的唯一潜真矩阵I-A°可逆(见文献[6,8]等),其中A°=(aij°)n×n是A(⊗)的唯一潜真矩阵,因此,灰色矩阵B(⊗)=(I-A(⊗))-1及其矩阵覆盖集[B]分别为:
B(⊗)=(I-A(⊗))-1-I, [B]=([bij])n×n=(I-[A])-1-I
(4)
其中[bij]是bij(⊗)(i,j=1,2,…,n)的区间覆盖集,(I-A(⊗))-1称为灰色列昂惕夫逆矩阵或灰色完全需求系数矩阵。显然,(I-A(⊗))-1的矩阵覆盖集(I-[A])-1是问题求解的关键。
1.3 灰色分配系数
由文献[1]等,定义中间产品的灰色分配系数hij(⊗)和最终产品的灰色分配系数hiy(⊗):
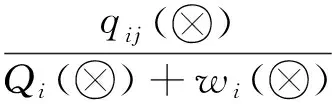
(5)
其中hij(⊗),hiy(⊗)满足以下等式:
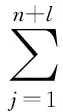
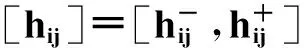
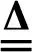
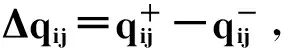
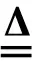
(6)
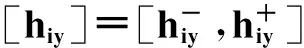
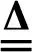
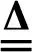
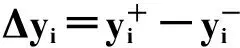
由文献[8]可知,[hij]1和[hij]2都是hij(⊗)的区间覆盖集;[hij]1和[hij]2都是hiy(⊗)的区间覆盖集。只不过前者是相对劣覆盖集,而后者是相对优覆盖集[7,8]。
当我们面临贫信息时,以上灰色系数及其覆盖集可以用来表示各部门间技术经济关系的大概范围。
根据实物型投入产出模型及以上的灰色系数,我们有灰色实物型投入产出模型。
假设灰色向量Q(⊗)=(Q1(⊗),…,Qn(⊗))T和Y(⊗)=(Y1(⊗),…,Yn(⊗))T,以及灰色矩阵I-A(⊗)可逆,则有灰色模型:
Q(⊗)=(I-A(⊗))-1Y(⊗)
(7)
又设[Q]=([Q1],[Q2],…,[Qn])T、[q]=([q1],[q2],…,[qn])T、[y]=([y1],[y2],…,[yn])T、[w]=([w1],[w2],…,[wn])T和[Y]=[q]+[y]-[w]分别是Q(⊗),q(⊗),y(⊗),Y(⊗)的向量覆盖集,则有以下灰色实物型投入产出模型的覆盖模型:
[Q]=(I-[A])-1[Y]
(8)
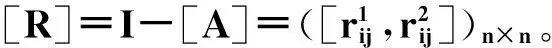
(9)

以下所有定理的证明分别类似于文献[12,15]等。
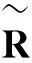
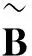
(10)
成立,其中p=col或row,‖‖col为矩阵或向量的列范数,‖‖row表示矩阵或向量的行范数,则对任意ε>0,必存在整数K0满足
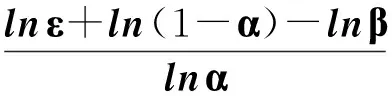
(11)
其中int(x)为不比x大的最大整数,有灰矩阵(I-A(⊗))-1的矩阵覆盖集[R]-1如下:
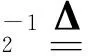
(12)
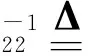
(13)
定理2 设公式(10)成立,并且
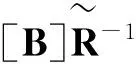
(14)
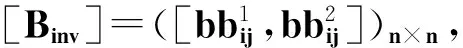
(15)
由于假设唯一潜真矩阵I-A0可逆,公式(10)对逆矩阵覆盖集的计算非常重要。否则,在I-[A]=[R]中将有一些白化矩阵是奇异矩阵,使我们无法计算矩阵覆盖集(I-[A])-1。
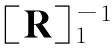
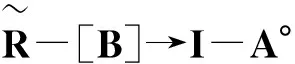
计算(I-[A])-1之后,利用公式(8)可以计算灰色总产出量Q(⊗)的覆盖集[Q],则我们可以采用统计数据的范围实现对经济系统的分析、预测与控制。
根据文献[1],灰色实物型投入产出分析还有另一种灰色模型
Q(⊗)=(I-H(⊗))-1Y(⊗)
(16)
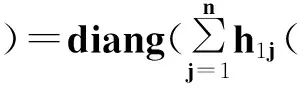
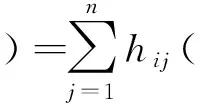
(17)
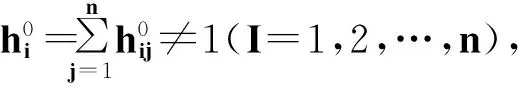
定理3 灰色矩阵I-H(⊗)是非奇异矩阵且逆矩阵为:
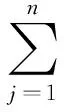
(18)
设[H]为H(⊗)的矩阵覆盖集,即

则有公式(16)的覆盖模型:
[Q]=(I-[H])-1[Y]
(19)
由公式(19)可知,求解Q(⊗)覆盖集[Q]的关键是计算矩阵覆盖集(I-[H])-1。
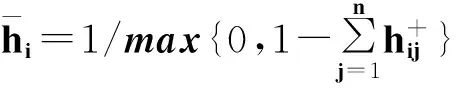
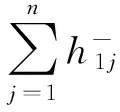
(20)
(21)
也成立,则有如下定理。
定理5 假设公式(21)成立,则(I-H(⊗))-1的矩阵覆盖集为:
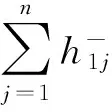
(22)
定理5表明,在贫信息条件下,我们可以实现对复杂经济系统的分析、预测与控制。
下面分别是矩阵覆盖集(I-[A])-1和(I-[H])-1的计算步骤。
算法1:
步骤1 获取数据的覆盖集[qij],[yi],[wi](i=1,…,n;j=1,…,n+l),给出精度ε>0;
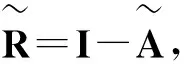
算法2:
步骤1 获取灰色统计数据的覆盖集[qij],[yi],[wi](i=1,…,n;j=1,…,n+l);
步骤3 若公式(21)不成立,则返回步骤1并使所有灰数据的扰动变小;
步骤4 根据公式(22)计算(I-[H])-1。
2 案例研究
下面通过一个简单案例验证本文提出的方法。
国民经济是一个复杂系统并由许多部门组成。为简便起见,假设有6个部门,即粮食(部门1)、棉花(部门2)、石油(部门3)、电力(部门4)、钢铁(部门5)和未列名产品(部门6)等。在贫信息条件下,获得灰色统计数据的覆盖集分别为[qij]、[Yi]和[Qi] (i,j=1,2,…,n)(见表3)。除部门4的单位是千瓦时外,其余部门的单位为万吨。要求在现有技术条件下分析国民经济下一年度的总产出。

表3 灰色数据的覆盖集表

表3 续
步骤1 各灰色统计数据的覆盖集见表3。
步骤2 由式(2)和(6)计算[Qi](见表3)和[hij](i,j=1,2,…,n)及矩阵覆盖集[H];

矩阵覆盖集[H]反映了列名产品间分布系数的大概范围,如[h23]=[0.0567,0.112]意味着每一百万吨部门2的实物产品要被分给部门3的数量在0.0567和0.1121之间。

矩阵覆盖集[A]表明,即使我们不知道列名产品间直接消费系数的真实值,但是可以知道大概范围,如a23∈[0.0214,0.0310]意味着部门3和5之间的直接消费系数的真值一定在[0.0214,0.0310]中。
(I-[H])-1=diag([1.0015,1.0018],[1.2470,1.5706],[2.8745,3.4281],[1.9291,1.9954],[2.8217,2.9416])
步骤5 设[Y′]=([1589,1603],[157,168],[331,336],[2200,2220],[803,809])T,则由公式(19)计算[Q′]:
[Q′]=([1591.4,1605.9],[159.8,263.9],[951.5,1151.8],[4244.1,4429.9],[2265.8,2379.8])T
向量覆盖集[Q′]表明了在技术水平不变条件下,为了满足下一年度的最终消费[Y′],各列名产品的下一年度的总产出。否则,国民经济系统将失去平衡。这个案例表明即使不能获取精确的统计数据,但是可以利用灰色实物型投入产出分析方法对复杂国民经济系统进行分析和控制。灰色实物型投入产出分析方法可以很大程度上减少统计数据的成本,给决策者更多的信息。
3 结束语
基于现实国民经济系统统计数据的贫信息特征,本文采用灰色系统理论的基本原理提出灰色实物型投入产出分析方法,包括灰色实物型投入产出表、灰色实物型投入产出模型及其应用,同时给出各种灰色系数和灰色模型的计算公式,以及采用模拟案例验证了灰色模型计算的合理性。该方法对贫信息条件下管理国民经济系统有非常重要的作用,为不确定环境下研究经济系统提供了有效的分析工具。
[1] 董承章.投入产出分析[M].北京:中国财政经济出版社,2000.
[2] Suh S. A note on the calculus for physical input-output analysis and its application to land appropriation of international trade activities[J]. Ecological Economics, 2004, (48): 9-17.
[3] Hoekstraa R, Berghb J. Constructing physical input-output tables for environmental modeling and accounting: framework and illustrations[J]. Ecological Economics, 2006, (59): 375-393.
[4] Bailey R,Bras B, Allen J. Measuring material cycling in industrial systems[J]. Resources, Conservation and Recycling, 2008, (52): 643- 652.
[5] Zeng L. Effects of changes in outputs and in prices on the economic system: an input-output analysis using the spectral theory of nonnegative matrices[J]. Economic Theory, 2008, (34): 441- 471.
[6] 李桥兴,林益.灰色系统理论基本体系研究[C]. Lanzhou: The 2010 Conference on Management in China, 2010. 158-163.
[7] 邓聚龙.灰理论基础[M].武汉:华中科技大学出版社,2002.
[8] 张岐山.灰朦胧集的差异信息理论[M].北京:石油工业出版社,2002.
[9] 肖新平,宋中民,李峰.灰技术基础及其应用[M].北京:科学出版社,2005.
[10] 李桥兴.灰色投入产出分析及直接消耗系数可拓调整研究[D].江苏:南京航空航天大学,2007.
[11] Li Q X, Liu S F. The foundation of the grey matrix and the grey input-output analysis[J]. Applied Mathematical Modelling, 2008, 32(3): 267-291.
[12] Li Q X, Liu S F. Some results about grey mathematics, kybernetes[J]. 2009, 38(3/4): 297-305.
[13] 李桥兴,王乃昂,吴妤.灰色朦胧集定义体系研究[J].系统科学学报,2014,22(3):39- 41.
[14] Li Q X. Grey dynamic input-output analysis[J]. Journal of Mathematical Analysis and Applications, 2009, (359): 514-526.
[15] Li Q X, Liu S F. The grey input-occupancy-output analysis[J]. Kybernetes, 2009, 38(3/4): 306-313.
[16] Li Q X. The grey departmental input-output analysis[J]. The Journal of grey system, 2011, 23(1): 101-112.
[17] Li Q X, Liu S F, Lin Y. Grey enterprise input-output analysis[J]. Journal of Computational and Applied Mathematics, 2012, (236): 1862-1875.
[18] 李桥兴,刘思峰.灰色地区投入产出分析[J].统计与决策,2014,(9):33-36.
Grey Physical Input-output Analysis
LI Qiao-xing1,2, LIU Si-feng2
(1.School of Management, Guizhou University, Guiyang 550025, China; 2.School of Eeconomics and Management, Lanzhou University of Technology,Lanzhou 730050, China; 3.College of Economics and Management, Nanjing University of Aeronautics and Astronautics,Nanjing 210016, China)
Because national economy is complex, we can not obtain the exact values of input and output of every product as we utilize the physical input-output analysis. By using grey system theory, we propose grey physical input-output analysis and get the covered solution formulas of grey model and grey coefficients. The grey physical input-output analysis can dispose the situation that the statistic datum are intervals, and the decision-makers can analyze, forecast and control the economic system under the uncertain situation, and the ability to resist risk can be improved. The modified case illustrates our method.
quantitative economics; grey physical input-output analysis; grey covered operation; complex economic system; grey coefficient
2012-12-25
中国博士后科学基金特别资助项目(200902321)
李桥兴(1973-),男,广西平乐人,副教授,博士后,系统科学与管理复杂性研究,数量经济理论与方法等。
F223
A
1007-3221(2015)03- 0165- 07

