三角直觉模糊决策的变权方法

余高锋, 李登峰， 邱锦明

(1.三明学院 信息工程学院,福建 三明 365004; 2.福州大学 管理学院,福建 福州 350108)



三角直觉模糊决策的变权方法

余高锋1, 李登峰2， 邱锦明1

(1.三明学院 信息工程学院,福建 三明 365004; 2.福州大学 管理学院,福建 福州 350108)

研究了属性值为三角直觉模糊数的多属性决策问题,提出了一种基于变权综合的决策方法。首先,针对三角直觉模糊数,提出一种新的三角直觉模糊排序方法;其次,定义了三角直觉模糊变权加权算术平均算子和三角直觉模糊变权加权几何平均算子;然后,提出一种基于三角直觉模糊变权集成算子的多属性决策方法;最后,数值算例说明了该方法的有效性。

变权向量；三角直觉模糊数;决策；集成算子

0 引言

自Atanassov[1,2]1986年提出直觉模糊集的概念, 由于直觉模糊集的特点是同时考虑隶属度、非隶属度和犹豫度三方面的信息, 直觉模糊集理论得到迅速发展, 其理论和方法也引起了研究人员的广泛关注。 文献[3～5]定义了三角直觉模糊数及其代数运算和排序方法, 并应用在多属性决策。文献[6]定义三角直觉模糊数的加权算术平均算子和加权平均几何算子, 并且用于多属性决策中。 文献[7]提出基于三角直觉模糊数的欧式期权二叉数定价模型。文献[8～10]定义了直觉模糊集集结算子及其在多属性决策中的应用和直觉模糊集多属性决策线性规划求解方法。文献[11,12]定义了直觉模糊梯形数的运算法则、大小比较方法、直觉模糊梯形集结算子, 并应用于多属性决策中。文献[13,14]对区间直觉模糊信息的集成方法进行了研究, 提出了区间直觉模糊算术平均算子、区间直觉模糊加权几何算子、区间直觉模糊加权平均算子、区间直觉模糊有序加权平均算子和区间直觉模糊混合集结算子，并应用于决策中。文献[15,16]利用数学规划方法和贴近度建立区间直觉模糊集多属性决策求解模型。文献[17]讨论直觉模糊梯形数的可能性均值方差, 提出一种可能性均值和方差排序方法。文献[18]建立基于决策者Vague信心度的模糊多准则方法。文献[19]建立基于模糊LINMAP法的具有不同类型信息的混合型多属性决策。文献[20]定义了三角直觉模糊的可能性均值和方差, 给出了一种基于可能性均值和方差之比的排序方法。文献[21]系统研究了三角直觉模糊的可能性均值、方差和相关系数，证明了其满足代数运算法则。文献[22]定义了关于三角直觉模糊数隶属函数和非隶属函数的可能性系数, 提出一种基于可能性系数的三角直觉模糊排序方法。

显然, 上述研究成果主要研究了直觉模糊数排序和信息集结方法, 该集结方法都是线性加权综合, 称其为常权综合方法。 然而在实际应用中, 这种方法具有一定的片面性, 有时候会导致不科学的决策结果。为了避免这个问题, 我国著名学者汪培庄教授于80年代率先提出变权综合思想。 文献[20～27]对变权的本质和原理进行了系统的研究, 定义了变权向量, 状态变权向量和均衡函数等一系列概念, 提出了变权综合原理, 并且得到了一种变权向量构造方法, 对状态变权向量和均衡函数的性质及其构造方法进行研究。综上所述，国内外关于考虑决策者心理状态和认知程度的三角直觉模糊决策方法文献还比较少, 因此本文提出一种基于变权综合的三角直觉模糊决策方法, 是有意义的。

1 预备知识

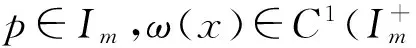
(1)ω(x)≥0;

(2)eTω(x)=1;

(4)变权综合函数v(x)=xTω(x)单调递增。则称ω(x)以p为激励策略的变权向量, 简称变权向量; 称p为变权向量ω(x)的激励策略。

2 三角直觉模糊决策的变权方法

2.1 三角直觉模糊数

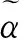
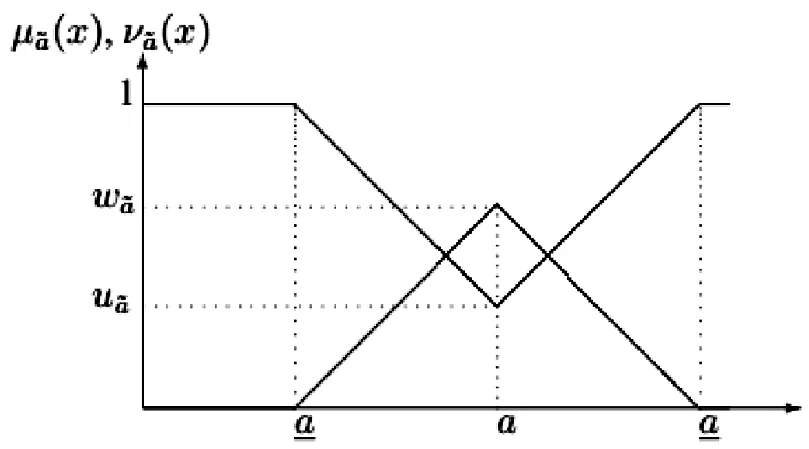
图1 三角直觉模糊数

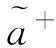
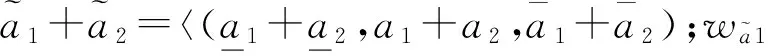
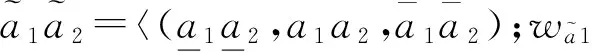
类似于直觉模糊集截集的定义，文献[2]定义了三角直觉模糊数的截集。

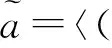
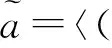
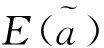
(1)

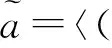
(2)

设λ∈[0,1]，λ反映决策者的偏好。若λ>0.5，决策者是风险型；若λ<0.5，决策者是保守型；若λ=0.5，决策者是中立型，一般情况下取λ=0.5。

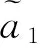
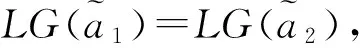
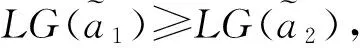
类似地可以定义小于关系、小于等于关系。

由于定义7给定的基于总精确度的三角直觉模糊排序方法具有一些有用的性质, 具体如下：

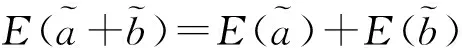
由式(1)和(2)可知, 性质1～4成立。

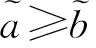
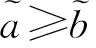
2.2 三角直觉模糊变权集成算子

根据三角直觉模糊数的运算法则, 定义三角直觉模糊信息集成相关算子, 如下:

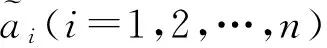
(3)

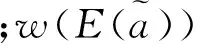
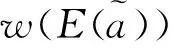
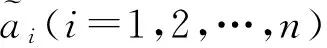
(4)

则称函数TIFN-WGA为n维TIFN的变权加权几何平均算子。

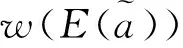
三角直觉模糊变权加权算术平均算子和三角直觉模糊变权加权几何平均算子与传统的算子相比,引入了变权的思想,综合考虑了属性值的期望值。当期望值高于参考点,权重函数是属性值的期望值增函数,即对于期望值高于参考点进行激励;反之,当期望值低于参考点,权重函数是属性值的期望值减函数,即对于期望值低于参考点进行惩罚,因此比传统的算子更加合理和科学,更能体现决策者的心理状态和认知程度。

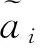
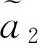
定理1和定理2利用数学归纳法证明,证明步骤如文献[12],因此这里省略。

2.3 决策方法

综上所述,提出一种基于三角直觉模糊变权集成算子的三角直觉模糊多属性决策方法,具体步骤如下:

(5)

(6)

Step 3 计算各个属性值得期望值。利用式(1), 可计算得各个属性值的期望为

Step 4 根据决策者的偏好和心理状态,给出参考点,构造变权向量。

Step 5 计算方案的综合值。利用式(5)或式(6),对方案xi(i=1,2,…,n)进行信息集成。

Step 6 对方案进行优劣排序。利用式(2),计算方案xi(i=1,2,…,n)的总精确度,从而得到方案xi(i=1,2,…,n)的优劣排序和最满意方案。

3 实例分析

3.1 数值例子

假定某个高校要招聘1位教师,经过初步筛选后,需要对3位候选人即x1、x2和x3,进行面试考核与最终招聘。该高校拟定如下5个考核指标即:科研能力g1、教学能力g2、工作经验g3、个性g4、自信g5假设初始权重为w=(0.14,0.3,0.12,0.3,0.14)T。假设各个候选人在各属性的评估信息经统计处理后,可表示为三角直觉模糊数,如表1所示。

表1 三角直觉模糊矩阵

决策步骤:

(1)各属性均为效益型, 选择式(6)进行规范化。 结果如表2所示。

表2 规范化的三角直觉模糊矩阵

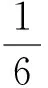
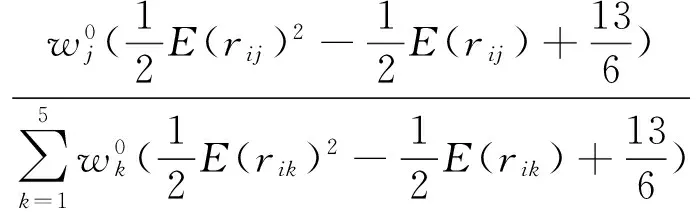
(3)利用三角直觉模糊变权集成算子，计算结果如表3所示。

(4)计算总精确度, 对候选人进行排序如表4所示。

表3 综合评价

表4 候选人排序

3.2 与相关文献比较分析

若将上例用文献[5]方法计算,得到各个方案与三角直觉模糊正理想方案的相对接近度分别为:ρ1=0.333,ρ2=0.526,ρ3=0.671。于是，三个候选人的排序为x3>x1>x2因此,最优的候选人为x3而本文最优候选人也是x3。

由此可知,本文的方法是合理的,TIFN-VWAA计算的结果比常权综合的区分度更加明显。由于规范化三角直觉模糊数的期望值都低于0.5,都受到了惩罚,所以TIFN-VWAA计算的值都比常权综合的值都低,因此变权决策效果比常权决策效果更能体现决策者的认知程度和心理状态, 即参考点可以取不同的值, 充分体现了决策过程的柔性, 结果更加合理。

4 结论

针对属性值是三角直觉模糊数的多属性决策问题，本文提出了一种三角直觉模糊变权集成算子决策方法,该方法的优点体现在：1)本文定义的三角直觉模糊变权加权算术平均算子和三角直觉模糊变权加权几何平均算子与传统的算子相比,引入了变权的思想,综合考虑了属性值的期望值,对于期望值高于参考点的进行激励,对于期望值低于参考点的进行惩罚,因此比传统的算子更加合理和科学,更能体现决策的心理状态和认知程度。2)本文定义的一种新的三角直觉模糊排序方法,比文献[3,4]的计算更方便,复杂度更低。

[1] Atanassov K T. Intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems, 1986, 20(1): 87-96.

[2] Atanassov K T, Gargov G, Interval valued intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems ,1989 (31): 343-349.

[3] Li D F, Nan J X, Zhang M J. A ranking method of triangular intuitionistic fuzzy numbers and application to decision making[J]. International Journal of Computational Intelligence Systems, 2010, 3(5): 522-530.

[4] Li D F. A ratio ranking method of triangular intuitionistic fuzzy numbers and its application to MADM problems[J]. Computers and Mathematics with Applications, 2010, 60(6): 1557-1570.

[5] 张茂军,南江霞,李登峰,等.带有三角直觉模糊数的多属性决策的TOPSIS[J].运筹与管理,2012,21(5):96-101.

[6] Zhang X, Liu P D. Method for aggregating triangular fuzzy intuitionistic fuzzy information and its application to decision making[J]. Technological and Economic Development of Economy, 2010, 16(2): 280-290.

[7] 张茂军,秦学智,南江霞.基于三角直觉模糊数的欧式期权二叉数定价模型[J].系统工程理论与实践,2013,33(1):34-140.

[8] Li D F, Chen G H, Huang Z G, Linear programming method for multiattribute group decision making using IF sets[J]. Information Sciences, 2010, 180(9): 1591-1609.

[9] Li D F, Multiattribute decision making method based on generalized OWA operators with intuitionistic fuzzy sets[J]. Expert Systems with Applications, 2010, 37(12): 8673- 8678.

[10] 万树平,董九英.多属性决策的直觉模糊梯形数法[J].控制与决策,2010,25(5):773 -776.

[11] 万树平.基于区间直觉模糊梯形的多属性决策方法[J].控制与决策,2011,26(6):857-- 860.

[12] 徐泽水,陈剑.一种基于区间直觉判断矩阵的群决策方法[J].系统工程理论与实践,2007,27(4):126-133.

[13] 徐泽水.区间直觉模糊信息的集成方法及其在决策中的应用[J].控制与决策,2007,22(2):215-219.

[14] Li D F, Closeness coefficient based nonlinear programming method for interval valued intuitionistic fuzzy multiattribute decision making with incomplete preference information[J]. Applied Soft Computing, 2011, 11(4): 3402-3418.

[15] Li D F, TOPSIS-based nonlinear-pogramming methodology for multiattribute decision making with interval valued intuitionistic fuzzy sets[J]. IEEE Trans on Fuzzy Systems, 2010, 18(2): 299-231.

[16] 万树平,张小路,李登峰.直觉梯形模糊群决策的可能性均值方差方法[J].系统工程学报,2012,27(6):782-788.

[17] 王坚强,张红宇,秦育智.基于决策者Vague信心度的模糊多准则方法[J].系统工程学报,2011,26(1):17 -22.

[18] Wan S P, Li D F. Fuzzy LINMAP approach to heterogeneous MADM considering the comparisons of alternatives with hesitation degrees[J]. Omega-The International Journal of Management Science, 2013, 41(6): 925-940.

[19] Wan S P, Li D F. Possibility mean and variance based method for multi-attribute decision making with triangular intuitionistic fuzzy numbers[J]. Journal of Intelligent & Fuzzy Systems, 2013, 24: 743-754.

[20] Wan S P, Li D F. Possibility mean, variance and covariance of triangular intuitionis-tic fuzzy numbers[J]. Journal of Intelligent & Fuzzy Systems, 2013, 24: 847- 858.

[21] Wan S P. Multi-attribute decision making method based on possibility mean,variance and covariance of triangular intuitionistic fuzzy numbers[J]. Int J of Uncertainty, Fuzziness and Knowledge-Based Systems, 2013, 2(21): 223-243.

[22] 汪培庄.模糊集与随机集落影[M].北京:北京师范大学出版社,1985:47-59.

[23] 李洪兴.因素空间理论与知识表示的数学框架(Ⅷ)[J].模糊系统与数学,1995,9(3):1-9.

[24] 刘文奇.均衡函数及其在变权综合中应用[J].系统理工程论与实践,1998,17(4):41- 47.

[25] 刘文奇.变权综合中的惩罚――激励效用[J].系统工程理论实践,1998,18(4):41- 47.

[26] 刘文奇.一般变权原理与多目标决策[J].系统工程理论与实践,2000,3(3):1-11.

[27] Wang X Z, Kerre E E. Reasonable properties for the ordering of fuzzy quantities(I)[J]. Fuzzy sets and systems, 2001, (118): 375.

Variable-weight Based Method for Intuitionistic Triangular Fuzzy Decision Making

YU Gao-feng1, LI Deng-feng2, QIU Jin-ming

(1.School of Information, Sanming University, Sanming 365004, China; 2.School of Management, Fuzhou University, Fuzhou 350108, China)

For multi-attribute decision making problems where the attribute values are intuitionistic triangular fuzzy numbers, a new decision making method is developed on the basis of variable-weight vector. Firstly, the concept of triangular intuitionistic fuzzy numbers is introduced, and a new ranking method of triangular intuitionistic fuzzy numbers is presented. Secondly, the triangular intuitionistic fuzzy variable-weight weighted averaging operator and triangular intuitionistic fuzzy variable-weight weighted geometric averaging operator are proposed. Then, a method for multiple attribute decision making based on triangular intuitionistic fuzzy variable-weight aggregation operators is developed. Finally, an illustrative example shows the effectiveness of the proposed approach.Key words:variable-weight vector; triangular intuitionistic fuzzy number; decision making; aggregation operators

2013-10- 09

国家自然科学基金重点项目(71231003);国家自然科学基金项目(71171055，70871117);福建省自然基金项目(2012J012802;2015J01287);福建省教育厅科技项目(JA14295);福建省大学生创新创业训练计划项目(201311311023) 。

余高锋(1986-) 男,助教,硕士,研究方向决策分析和博弈论等研究；李登峰( 1965-)，男，广西人，教授，博导，研究方向决策与对策。

C934

A

1007-3221(2015)03- 0120- 07