一种改进马氏距离的最近邻数据关联算法

王晓君,裴福俊,刘红云

(北京工业大学电子信息与控制工程学院,北京 100124)

一种改进马氏距离的最近邻数据关联算法

王晓君,裴福俊,刘红云

(北京工业大学电子信息与控制工程学院,北京 100124)

针对最近邻数据关联算法关联正确率较低,容易导致错误关联的问题,本文提出了一种改进的最近邻数据关联算法。该算法通过计算传感器的测量值与地图已有特征之间数据关联的概率,分析了预测向量和观测向量的协方差对数据关联算法的影响机制,提出了预测向量和观测向量的协方差辅助计算马氏距离的改进最近邻数据关联算法,并给出了算法的具体实现流程。最后,通过仿真实验结果表明,改进的最近邻算法在几乎不增加计算时间的情况下,具有更高的数据关联正确率,将该算法应用到同时定位与地图创建中,运动轨迹的估计更接近于实际的轨迹。

同时定位与地图创建;数据关联;最近邻算法;马氏距离

文献[1-2]于1986年提出机器人同时定位与创建地图(simultaneous localization and mapping, SLAM),并成为了在室内、室外、海下等多种环境中解决机器人自主导航的重要技术。SLAM算法可描述为:首先,移动机器人在运动过程中,为了逐步增量式地建立一个连续的环境地图,根据自身的传感器来测量周围环境信息;然后,利用数据关联对传感器测量的环境特征与地图中保存的特征进行匹配,建立地图辅助的观测信息模型;最后,应用最优估计方法完成对机器人位姿和环境地图的同步估计[3]。因此,在SLAM计算过程中,为了完成最后的状态估计,数据关联是其中关键的条件与基础,在对机器人定位与地图创建的准确性上,数据关联的正确率对其造成很大的影响。数据关联算法必须满足2个要求:(1)关联准确率高;(2)算法运行时间少。当前,最近邻域(nearest neighbor,NN)[4]算法、联合概率数据关联算法[5](joint probabilistic data association,JPDA)以及联合相容分枝定界算法[6](joint compatibility branch and bound,JCBB)是最基本的数据关联算法。JPDA和JCBB算法虽然数据关联正确率略高,但是若所观测的特征较多时,由于其计算复杂度较高,限制了其实时应用。而NN算法由于其原理简单,易于实现的特点,仍然是应用最为广泛的数据关联算法。但是,NN算法采用马氏距离最短的特征作为最佳匹配条件,其数据关联正确率低,容易造成机器人的状态估计误差。针对NN算法的问题,很多学者提出了NN算法的改进算法。文献[7]提出了一种最近邻联合概率数据关联方法,其思想是将JPDA算法与NN算法相融合;文献[8]分析了最近邻数据关联算法的不足,并在此基础上提出了联合兼容性检验的关联算法;文献[9]提出了一种基于最近邻动态联合数据关联算法,该算法采用多帧观测数据的关联结果来动态去除观测特征中的伪特征;文献[10]在基于马氏距离规则最近邻算法基础上提出了一种基于多规则的数据关联算法,该算法采用多规则联合匹配的方式,从多个可能的关联假设中识别出正确的关联假设。上述几种算法存在以下不足:1)均通过融合其他关联算法来提高数据关联的准确性,不可避免的增加了计算复杂度;2)均重点关注了关联匹配正确率,并未考虑传感器的测量值与地图已有特征之间数据相关联的概率,忽略了观测信息与预测信息误差对匹配结果的影响。

在SLAM计算过程中,错误的数据关联有以下三种可能:1)由于对机器人运动方程和传感器观测方程的线性化处理而导致的数据关联假设错误;2)环境特征密集而造成的测量误差;3)机器人位置误差的积累。针对这些问题,最近邻算法仅依靠马氏距离并不能得到正确的数据关联。本文通过将预测向量和观测向量协方差引入到数据关联公式,提出了一种改进的最近邻关联算法,重点解决由测量误差所带来的错误数据关联问题。将本文提出的改进算法与基于马氏距离的数据关联算法相比较,改进算法在计算复杂度和系统运行时间两方面性能几乎与NN算法相同,但数据关联的正确率显著提高,将改进的算法应用到SLAM系统中,仿真结果表明了改进后的算法估计精度更高,运动轨迹更加接近其真实路径。

1 基于最近邻算法的数据关联

1.1 SLAM数据关联的数学模型

数据关联是用于完成传感器的观测值与地图中已有特征之间的关联匹配,是SLAM算法实现的关键技术。

即在一个状态向量中,将地图环境特征与机器人位姿状态存储进去,通过传感器来观测周围环境的特征信息并建立观测向量。利用最优估计理论来估计地图特征和机器人位姿,从而实现对机器人的同时定位与创建地图,SLAM算法流程如图1所示[10]。

从图1中可以看出,数据关联是SLAM过程的关键步骤,也是整个算法实现状态估计的前提和基础,其关联正确率将直接影响机器人定位与地图创建的准确性。

图1 SLAM算法流程图

1.2 最近邻算法

在SLAM过程中,应用最近邻数据关联算法的具体步骤如下。

2 改进的最近邻关联算法

2.1 最近邻算法的局限性

在数据关联过程中,导致错误关联的可能性有3种:(1)把已有特征看作新的特征,导致计算复杂度增加;(2)把新的特征看作已有的特征,有可能导致地图的发散;(3)把已有的特征与另一已有的特征相关联,从而出现错误的数据关联。

虽然基于马氏距离的最近邻算法考虑了传感器观测周围环境的概率特性和特征参数表达的位置信息,但仍然不可避免的存在错误关联的可能性,最近邻算法造成错误关联的情况主要有以下三种情况:

(1)由于对机器人的运动方程和传感器的观测方程进行了线性化处理,使机器人的位姿和地图出现过于乐观的估计,从而使得正确的数据关联假设造成过大的马氏距离,导致其不能识别正确的数据关联假设,出现多重数据关联[11],而为了解决该问题,则需要增大马氏距离的阈值,但增大阈值又会导致计算量的增加,影响计算速度。文献[11]引用了动态阈值的概念,对关联门进行限制,从而减少了所需计算的数据关联数量,在不影响数据的正确关联率的情形下,缩小了计算时间。

(2)在环境特征相对密集,并且机器人里程计的误差又较大的情况下,容易出现错误的数据关联。

(3)而随着机器人运动距离的增加,其位置误差会不断积累,仅仅依据马氏距离进行数据关联将无法给出正确的关联结果。文献[8]的思想是将数据关联的范围限制在局部的可能区域中,为了实现这一思想调整传感器的有效量程和机器人的位姿,在一定程度上改善了由于位置误差积累所造成错误的数据关联假设。

综上所述,数据关联的正确与否关键在于测量误差的大小,而最近邻算法中的马氏距离作为数据关联的依据无法保证产生正确的数据关联结果,在实际应用中,最近邻算法其中一项复杂而又难以完成的任务就是找到一个适合的马氏距离阈值。本文研究的重点在于如何改进马氏距离来减小由于测量误差所带来的影响,从而提高关联正确率。

2.2 改进的最近邻算法

针对最近邻数据关联算法的不足,一般的改进方法是引入其他算法来动态调整马氏距离的阈值,从而提高最近邻算法的准确性。但是,这些改进方法不可避免的会增加算法的计算复杂度,同时,这些方法只是关注了关联匹配过程本身,并未考虑由于传感器测量误差带来的影响。

由(11)式可知,地图中已有特征与观测值的关联程度不仅仅与马氏距离有关,而观测值和预测值的协方差同样也影响着数据关联的准确性。

为了阐明观测值和预测值的协方差对数据关联准确性的影响,分别在如图2所示的两种不同的情况下进行分析。图2中,O1和O2表示观测值, P1和P2表示预测值,左图表示两个观测值同时对应于同一个预测值,右图表示同一个观测值对应于两个预测值。从左图可以看出,无论应用NN算法还是NLML算法,其数据关联的结果均为O1与P1相匹配。相反,右图中若应用NN算法,其马氏距离O1P1O1P2,O1与P2相匹配,则得到正确的关联结果。由以上两种情况可知,当判定数据关联时,其马氏距离的最小化并不等同于NLML的最小化,观测值和预测值的协方差也影响着关联匹配结果,而当环境相对复杂时,仅仅应用马氏距离并不能得到正确的关联结果,而必须考虑观测值和预测值的协方差的影响。

基于以上分析,在关联过程中,本文通过引入观测与预测信息,提出了改进马氏距离的数据关联算法,该改进算法通过计算传感器所观测到的特征值与地图中已有特征相关联的可能性概率,并对其所求概率取负对数得到,简称NLML算法, 当NLML取值最小时,则其关联概率最高,同时得到关联最佳匹配。本文提出的数据关联算法的具体流程如表1所示。

图2 NN算法与NLML算法的对比分析

表1 NLML算法的流程

3 仿真与分析

3.1 仿真实验模型

本文所采用的SLAM问题的数学模型为:一个在未知环境中自主移动的机器人,其模型示意图如图3所示。

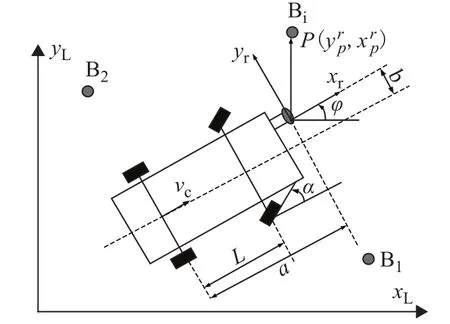
图3 移动车辆模型

图3中,xL与yL是车辆中心在全局坐标系下的位置坐标,L为车辆前轴与后轴之间的距离,a为激光器中心到车辆后轴中心之间的距离,b为激光器中心到车辆中轴之间的距离。移动机器人的运动模型通常用以下模型表示为

式(12)中,X(k)表示机器人在第k步时的运动状态,u(k)表示机器人的运动控制,w(k)为高斯噪声,其协方差为Q(k)。则在全局坐标系中机器人的运动模型可以表示为式(13),其中x(k)、y(k)、φ(k)为k时刻机器人的位置和方位角,α表示车轮转过的角度,vc表示车辆行驶的速度,ΔT为采样时间间隔。则移动机器人的运动模型表示为

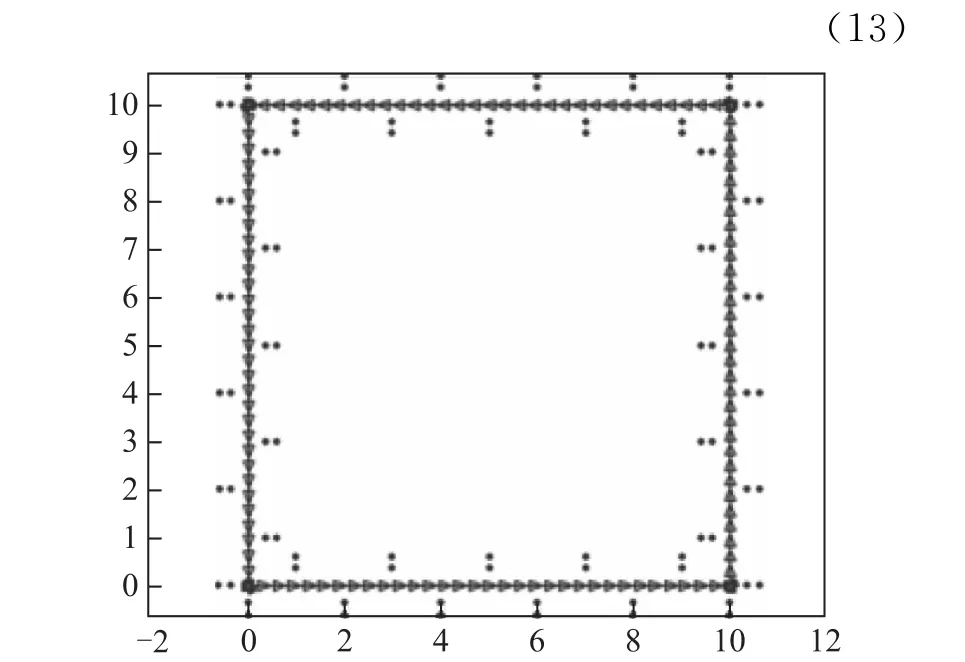
图4 仿真环境示意图

SLAM系统的观测模型如式(14)所示,

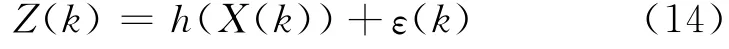
式(14)中,Z(k)表示为k时刻观测到的环境特征点,h(X(k))为特征点的观测函数,ε(k)为高斯白噪声,其协方差为R(k)。在全局坐标系下机器人的观测模型可表示为

式(15)中,下标p表示环境特征点的坐标在机器人坐标系下的投影。

3.2 仿真结果分析

实验所用的环境是文献[8]设计的仿真实验平台,如图4所示。在仿真试验中,系统围绕一个正方形(10 m×10 m)的轨迹移动,总共走了168 步,图4中圆点表示可观测的路标,三角形表示移动机器人,在移动过程中机器人用激光传感器持续测量了88个路标,且路标平均分布在轨迹的内外两侧。

图5分别为采用NN、NLML两种数据关联算法时每一步所需的执行时间。NLML算法与NN算法相比,虽然理论上其计算复杂度有所增加,但从图5中的仿真结果可以看出,NLML算法在数据关联过程中的执行时间并没有大幅度的延长,每一步的运行时间仅比NN算法平均多用0.007 s。图6和图7中黑色区域表示系统每一步的正确关联率,白色区域表示系统每一步的错误关联率。其中:

图5 NN和NLML每一步运行时间对比

·True positive:相关联的正确率。

·True negative:新路标加入地图中的正确率。

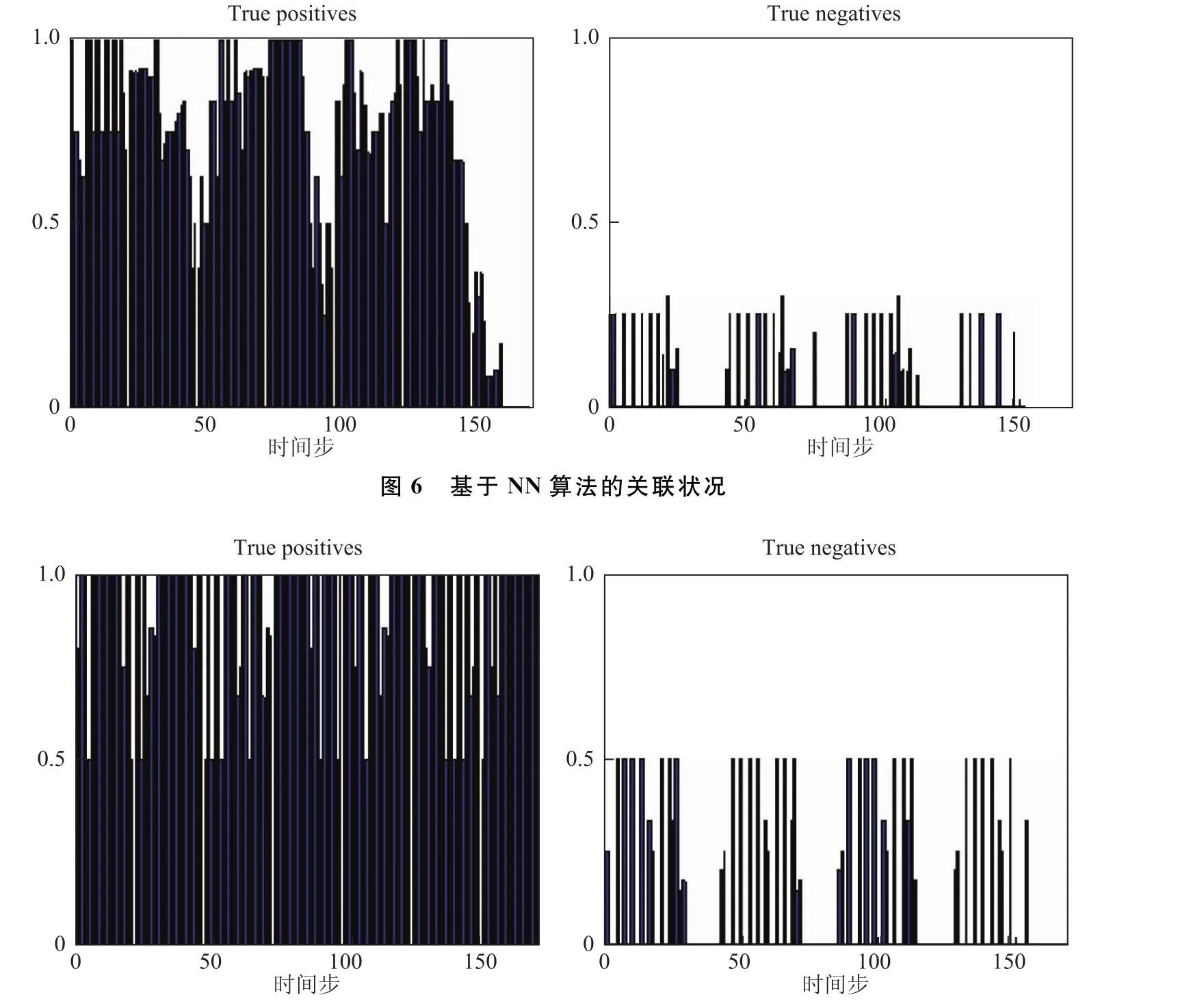
图7 基于NLML算法的关联状况

由图6中可见,由于受机器人运动模型和观测模型线性化处理以及里程计误差较大的影响,基于NN算法的每一步数据关联正确率并不高,相比之下,由条件概率所求得的NLML算法,考虑到了传感器观测特征与地图已有特征的所有关联可能性,能够很好的弥补NN算法的局限性。从图6和图7的分析比较可看出,基于NLML算法的每一步关联正确率大大提高,同时将传感器所观测到的特征值作为新路标加入地图中的正确率也有很大的提高。

通过图8可以看出:与NN算法相比较,本文的NLML算法具有更高的定位精度,车辆在x方向、y方向以及角度的定位误差更小。

图9和图10是分别采用NN算法与NLML算法实现的SLAM算法的估计结果:图9和图10中红色线为车辆的真实路径,红色点为环境的真实路标点,蓝色线为SLAM系统估计的车辆运动轨迹,蓝色点为SLAM系统估计的特征点坐标。将图9和图10进行对比分析可以看出,相对于基于NN算法的SLAM系统,基于NLML算法的SLAM系统所估计的机器人运动轨迹也更接近于真实的路径,特征点也更接近于真实的特征点。

由以上仿真实验可以证明,NLML算法有效弥补了NN算法的局限性,同时NLML算法的计算复杂度并不会影响系统的整体实时性,大大提高了数据关联的正确率。相较于NN算法,基于NLML算法的SLAM系统具有更好的估计精度。

4 结束语

针对最近邻数据关联算法关联准确度问题,本文通过对数据关联的条件概率进行分析,可以得出数据关联度的精度不仅仅与马氏距离有关,观测值和预测值的协方差同样影响着数据关联的准确性。基于这一分析,本文将观测值和预测值的协方差引入到数据关联过程中,提出了一种改进马氏距离计算方法的最近邻数据关联算法,并给出了算法的具体实现流程。最后,通过仿真实验对提出的改进最近邻算法进行验证,通过仿真结果可以看出,本文提出的改进最近邻算法在几乎不影响算法运行时间的情况下,数据关联正确率有了明显的提高。同时,将该算法应用到SLAM系统中,仿真结果表明应用该算法的SLAM系统能够很好地估计出车辆的运动轨迹,更加接近机器人的真实路径。因此,本文提出的改进最近邻数据关联算法具有更好的计算效率和关联准确度,更适合于SLAM系统的实际应用。

图8 基于NN和NLML算法定位误差对比

图9 基于NN算法的运动轨迹

图10 基于NLML算法的运动轨迹

[1] DISSANAYAKE M W M G,NEWMAN P,CLARK S,et al.A solution to the simultaneous localization and map building (SLAM)problem[J].IEEE Transactions on Robotics and Automation,2001,17(3):229-241.

[2] SMITH R,SELF M,CHEESEMAN P.Estimating uncertain spatial relationships in robotics[EB/OL].(2005-10-12) [2014-08-12].http://www.cs.uml.edu/～holly/91.549/readings/smith90stochastic.pdf.

[3] DURANT-WHYTE H,BAILEY T.Simultaneous localization and mapping:part I the essential algorithms[J].Robotics and Automation Magazine,2006,13(2):99-110.

[4] BAILEY T.Mobile robot localisation and mapping in extensive outdoor environments[D].Sydney:The University of Sydney,2002.

[5] FITZGERALD R J.Development of practical PDA logic for multitarget tracking by microprocessor[C]//The Institute of Electrical and Electronics Engineers(IEEE).Proceedings of American Control Conference,1986.Seattle:IEEE,1986:889-898.

[6] NIETO J,GUIVANT J,NEBOT E.DenseSLAM:simultaneous localization and dense mapping[J].The International Journal of Robotics Research,2006,25(8):711-744

[7] CHANG K C,BAR S Y.Joint probabilistic data association for multitarget tracking with possibly unresolved measurements and maneuvers[C]//The Institute of Electrical and Electronics Engineers(IEEE).Proceedings of American Control Conference,1983.San Francisco:IEEE,1983:466-471.

[8] NEIRA J,TARDÒS J D.Data association in stochastic mapping using the joint compatibility test[J].IEEE Transactions on Robotics and Automation,2001,17(6):890-897.

[9] 周武,赵春霞,张浩峰,等.动态联合最近邻算法[J].电子学报,2010,38(2):359-365.

[10]郭帅,马书根,李斌,等.VorSLAM算法中基于多规则的数据关联方法[J].自动化学报,2013,39(6):883-894.

[11]HUANG Shoudong,DISSANAYAKE G.Convergence analysis for extended Kalman filter based SLAM[EB/OL].(2006-01-31)[2014-08-12].http://services.eng.uts.edu.au/～sdhuang/ICRA06_438_final_IEEE.pdf.

[12]STONE L D,BARLOW C A,CORWIN T L.Bayesian multiple target tracking[M].Norwood,MA:Artech House,1999.

Novel Nearest Neighbor Data Association Algorithm Based on Improved Mahalanobis Distance

WANG Xiaojun,PEI Fujun,LIU Hongyun
(College of Electronic Information and Control Engineering,Beijing University of Technology,Beijing 100124,China)

In the mobile robot simultaneous localization and map building,nearest neighbor data association algorithm has been widely applied,because of its simple principle and easy to implement,but its correct association is low,and easily to cause the error correlation.In view of its shortcomings,this paper puts forward an improved nearest neighbor data association algorithm.By calculating the probability of the data association between the observed value of the sensor and the existing map features,analysis of the prediction and observation vector covariance influence mechanism on data association algorithm,proposed the prediction vector and the observation vector covariance auxiliary calculating the Mahalanobis distance to improve the nearest neighbor data association algorithm,and gives the specific implementation process of the algorithm.In the end,the simulation results show that the improved mahalanobis distance algorithm can’t affect the overall system uptime,at the same time,its data association has a higher accuracy,applied to the robot positioning and map building,the estimated trajectory is more accurate.

simultaneous localization and mapping;data association;nearest neighbor;mahalanobis distance

P228

A

2095-4999(2015)-04-0050-07

2014-10-18

北京市青年拔尖人才培育计划(CITTCD201304046)。

王晓君(1990—),女,黑龙江大庆人,硕士生,从事机器人自主导航算法的研究。

王晓君,裴福俊,刘红云.一种改进马氏距离的最近邻数据关联算法[J].导航定位学报,2015,3(4):50-56,73.WANG Xiaojun,PEI Fujun,LIU Hongyun.Novel Nearest Neighbor Data Association Algorithm Based on Improved Mahalanobis Distance[J].Journal of Navigation and Positioning,2015,3(4):50-56,73.

10.16547/j.cnki.10-1096.20150410