一堂探究活动课的学习心得体会
尉琳
2014年10月中旬,笔者参加了北师大举办的《中国梦﹒教育梦》培训班,其中一节探究课给我留下了深刻的印象,现将本节课及其听课的一些心得体会呈现如下:课题是:《探索三角形分割成两个等腰三角形的条件》,执教者浙江省绍兴市柯桥区教师发展中心的特级教师姚志敏,本节课生动幽默. 一、教学过程精彩呈现
公开课的教学过程:
1. 新旧知识联系
师:有一个三角形,我任意剪一刀,会得到哪两个图形?如果我要得到两个等腰三角形,我该如果剪呢?
众生:不知道原三角形的角度,无法分.
师:如果三角形的度数分别是36°,72°,72°,你可以帮忙办到吗?生1:平分36°.
师追问:好的,还有其他分法吗?生2:平分72°.
师:很好,很聪明,姚老师真的很高兴!(哈哈,活跃气氛),如果内角改成25°,50°,105°,你能办到吗?
生3:从105°大角中分出一个25°小角.
师:非常聪明,请你设计一个三角形,使这个三角形可以被分割成两个等腰三角形.
学生陷入了沉思,积极开动脑筋,教师让学生把想到的写到黑板上来,答案有:(1)45°,45°,90°;(2)30°,60°,90°; (3)108°,36°,36°;(4)41°,123°,16°.
师:真的很聪明啊,有些我们老师都没有想到啊,特别是第四名同学写的. 任何三角形都能被分割成两个等腰三角形吗?揭示本节课课题:探索三角形可以被分割成两个等腰三角形的条件.
2. 探索猜想,获得新知
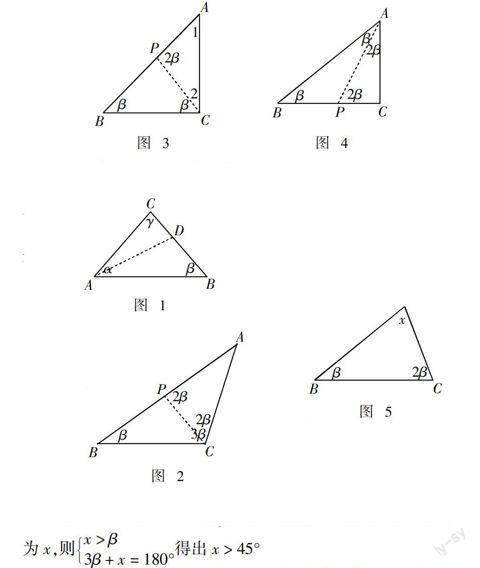
师:如图1,△ABC中,∠A = α,∠B = β,∠C = γ,α,β,γ满足什么条件时,原三角形能被分割成两个等腰三角形.
生在师的点拨下,共同推导出结论. 若从α分割出β,则△ABD是等腰三角形,下面说明△ACD能否是等腰三角形.
分类讨论:若CA = CD,则α = 3β;若DA = DC,则可推出α = 90°;若AC = AD,则2β = γ.
分别得出结论:(1)原三角形有一个角是另一个角的2倍;(2)原三角形是直角三角形;(3)原三角形有一個角是另一个角的3倍.
3. 验证猜想,举例应用
师:(1)已知△ABC中,∠B = β,∠C = 3β,△ABC一定能够被分割成两个等腰三角形吗?(图2)
生:分3倍角.
师:如果把三角形的内角改成37°,111°,32°,你还能分吗?
师:(2)已知△ABC是直角三角形,∠C = 90°,△ABC一定能够被分割成两个等腰三角形吗?
生:分直角.
师:如何说明呢?
师生共同说明:利用同角的余角相等可证明△ACP是等腰三角形. (图3)
生:还可取AP的中点.
师:非常好,利用刚学过的在直角三角形中,斜边的中线等于斜边的一半. 不从直角分,能不能分出来?若∠A比∠B大,可得∠B = 22.5°,即可得一个角是另一个角的3倍(图4),为了体现分类的严谨性,我们把这种情况就归到3倍角的情形.
下面感受第3种2倍角的情形:
师:(3)△ABC中,设∠A = 38°,∠B = 76°,∠C = 66°,怎么分呢?生:分2倍角.
师:△ABC中,设∠A = 36°,∠B = 96°,∠C = 48°,如何分?生:分2倍角.
(好像有疑问?下面开始有小范围不同的声音)
生:不能画.
师总结:三角形有一个角是另一角的2倍,不一定能分成两个等腰三角形. 需要增加什么条件呢?这个角有什么限制呢?如果,P为△ABC中BC边上一点.
问题:你会计算“当原三角形一个角为另一个角的2倍时,若分割成两个等腰三角形”,第三个角有取值范围吗?
(这个问题对初二的学生来说是有很大难度的,下面主要是教师在讲过程)
师:要能从第三个角分,肯定不能为最小角. 设第三个角为x,则x > β3β + x = 180°得出x > 45°
师生共同总结出以下结论:一个三角形可以被分割成两个等腰三角形的条件:
(1)原三角形一个角是另一个角的2倍(分第三个角,第三个角要大于 45°);
(2)原三角形一个角是另一个角的3倍(分3倍角);
(3)原三角形是直角三角形(分直角).
本节探究课涉及的数学思想有:猜想—验证、分类讨论、反例说明等.
这时再回过去验证同学们一开始写在黑板上的例子是否正确,前后呼应.
二、对本节探究课的几点思考
(1)探究课课题的来源
本节课是初二学生在刚学习过全等三角形,等腰三角形等内容后的一堂探究课,姚老师说一般的探究课课堂需要一个小时左右,本节课的课堂是执教者在做题的过程中摸索出来的. 如何将一个三角形分割成两个等腰三角形学生在学习新课时作业中是遇到过的,或许还不止一次遇到同类型的题目,教师在学生有了部分感性认识的基础上,通过设计各种问题串,层层追问,设计有阶梯性的问题,让学生在感性认识的基础上获得理性认识.
(2)探究课带给学生的好处
有些探究课虽然不一定能够上升为某种高度,但我想至少能够收获某些结论,这些结论能够帮助我们快速地解决一些小问题,所以这种探究课在初中课堂上应该多加呈现,这是对教师教学工作的一种促进,也是对学生思维的一种训练.