对一堂操作型问题复习课的反思

周继云

三角板是学生最常用的学习工具， 以三角板为道具，以学生常见、熟悉的几何图形为载体， 并辅之以平移、旋转等变换手段的问题， 能为学生提供动手实践操作设计的空间，较好地考查了学生观察、实验、比较、联想、类比、归纳的能力以及运动变化、分类讨论思想等的综合运用能力. 这类操作性的题目格调清新，立意新颖， 充分体现了课标中提出的“培养学生动手动脑、实践探索的能力”的要求，既注重基础知识，同时又具有很强的综合性.

1. 设计思路

初三年级第二轮专题复习中所用的问题不仅要起到复习知识的作用，更要用经过精心设计的问题反映解决一类问题的思想与方法. 本节课主要借助三角板的旋转变换，选择一些注重知识形成过程、体现数学思想方法的探索性问题，通过动手操作和理性的思考，总结归纳出解决此类问题的一些基本思路和方法.

为了体现复习课的知识目标，并关注技能与思想方法目标的实现，本课的设计思路为“特殊到一般”，具体表现为：

（1）题目的设置从特殊到一般，即从两个直角顶点重合、一个直角顶点与斜边中点重合，到一个直角顶点与斜边上任意一点重合、一个锐角顶点与斜边上的中点重合；

（2）相应的解题方法从特殊到一般，即从利用三角形全等，到利用三角形相似.

2. 复习课题目来源

最初是在历年的中考试题中挑选复习题的，目标是那些以三角板为载体的试题，比如：

题1 （山东临沂07中考25题）如图1，已知△ABC中，AB = BC = 1，∠ABC = 90°，把一块含30°角的直角三角板DEF的直角顶点D放在AC的中点上（直角三角板的短直角边为DE，长直角边为DF），将直角三角板DEF绕D点按逆时针方向旋转.

（1）在图1中，DE交AB于M，DF交BC于N. 证明DM = DN；

（2）继续旋转至如图2的位置，延长AB交DE于M，延长BC交DF于N，DM = DN是否仍然成立？若成立，请给出证明；若不成立，请说明理由；

（3）继续旋转至如图3的位置，延长FD交BC于N，延长ED交AB于M，DM = DN是否仍然成立？请写出结論，不用证明.

题2 （徐州08年中考28题）如图4，一副直角三角板满足AB = BC，AC = DE，∠ABC = ∠DEF = 90°，∠EDF = 30°【操作】将三角板DEF的直角顶点E放置于三角板ABC的斜边AC上，再将三角板DEF绕点E旋转，并使边DE与边AB交于点P，边EF与边BC于点Q

在旋转过程中，

（1）如图5，当■ = 1时，EP与EQ满足怎样的数量关系？并给出证明.

（2）如图6，当■ = 2时EP与EQ满足怎样的数量关系？，并说明理由.

（3）根据你对（1）、（2）的探究结果，试写出当■ = m时，EP与EQ满足的数量关系式为 ，其中的取值范围是 （直接写出结论，不必证明）

题3 （湖南常德06中考试题26）把两块全等的直角三角形ABC和DEF叠放在一起，使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合，其中∠ABC = ∠DEF = 90°，∠C = ∠F = 45°， AB = DE = 4，把三角板ABC固定不动，让三角板DEF绕点O旋转，设射线DE与射线AB相交于点P，射线DF与线段BC相交于点Q.

（1）如图7，当射线DF经过点B，即点Q与点B重合时，易证△APD∽△CDQ.此时，AP × CQ = .

（2）将三角板DEF由图7所示的位置绕点O沿逆时针方向旋转，设旋转角为α.其中0° < α < 90°，问AP × CQ的值是否改变？说明你的理由.

由于本课的主旨在于让学生在图形变换的“变化”过程中寻找“不变”的量和关系，因而初稿就直接删掉了研究变量之间的函数关系这一类题.

3. 试教反思

经过试讲发现几个问题：

（1）课题引入“三角板中蕴含了哪些数学知识？”问题设置不合理，范围太广学生回答时有如大海捞针，与本课相关的知识回答不到位，所用时间太多.

（2）山东临沂的试题与徐州试题的第一题 本质上是相同的，故显得重复；

（3）由于这些题都是操作探究型问题，相对有些思维的难度，直接在课堂上解决，学生的思考时间太短，未能达到预期的教学目标.

修改方案：

（1）引入问题：“三角板中蕴含哪些数学知识？”调整成“三角板中蕴含的知识分类：与边有关的有哪些？与角相关的有哪些？与高相关的有哪些？”

（2）把山东临沂与徐州的两个试题进行了改编合并成一个题，在小题的设置上作出相应的调整：【探究一】即问题1，将其第二小题的“如图”改成让学生根据题意画出相应图形，意在训练学生的审题、画图等能力.

（3）将改编的【问题】提前发给学生进行课前预习，课堂主要解决的问题是方法点拨和归纳；问题3作为课堂练习“试一试”，其中也设置了根据题意画图这个环节，检查学生的掌握情况.

修改后如下：

4. 施教教案

【课题引入】：三角板这个学习工具包含的数学知识很多，我们可以将其简单分类：与边相关的有哪些？与角相关的有哪些？与斜边上的高相关的有哪些？

【基础练习】

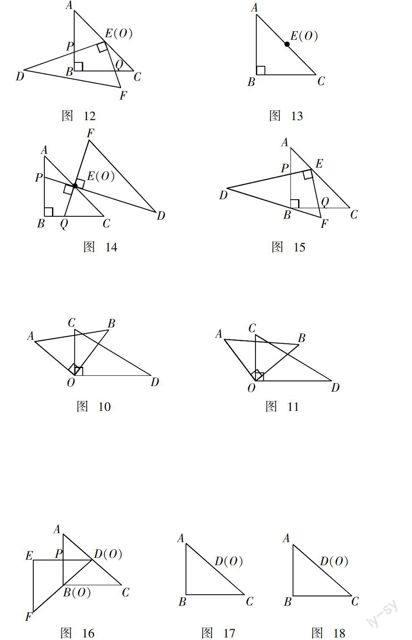
1. 如图（10），将一副三角板的直角顶点重合，摆放在桌面上，若∠AOD = 145°，则∠BOC = 度，∠AOD + ∠BOC =

度.

变式：若∠AOD = α，则∠AOD + ∠BOC = 度.

2. 如图（11），将一副直角三角板重叠，直角顶点重合，若∠AOC = 40°则∠DOB = 度.

变式：若∠AOC = α，则∠DOB = 度.

【探索发现】

问题：一副直角三角板满足AB = BC，AC = DE，∠ABC = ∠DEF = 90°，∠EDF = 30°，将三角板DEF的直角顶点E放置于三角板ABC的斜边AC上，再将三角板DEF绕点E旋转，

【探究一】当E与AC中点O重合（即■ = 1）

（1）如图12，在旋转过程中，边DE交边AB于点P， 边EF交边BC 于点Q， 猜想并写出EP与EQ 满足的数量关系，证明你的猜想.

（2）若继续旋转，当边DE与AB的延长线交于点P，EF的延长线与BC延长线交于点Q，请在图13中画出图形，（1）中的结论是否成立？若成立，写出结论不需要证明. 若不成立，说明理由.

（3）如图14，FE延长线与BC边交于Q，DE延长线与AB边交于P，（1）中的结论是否成立？若成立，写出结论，不需要证明；若不成立，说明理由.

【探究二】当E不与AC中点O重合，如■ = 2时，如图15，边DE与边AB交于点P，边EF与边BC交于点Q，猜想EP与EQ满足的数量关系？并证明你的猜想.

【探究三】根据你对一、二的探究结果，试写出当■ = m时（边DE与边A B交于点P，边EF与边BC交于点Q），EP与EQ满足的数量关系式为 （直接写出结论，不必证明）

【学以致用】

试一试：把两块全等的直角三角形ABC和DEF叠放在一起，使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合，其中∠ABC = ∠DEF = 90°，∠C = ∠F = 45°， AB = DE = 4，把三角板ABC固定不動，让三角板DEF绕点O旋转，设射线DE与射线AB相交于点P，射线DF与线段BC相交于点Q.

（1）如图16，当射线DF经过点B，即点Q与点B重合时，易证△APD∽△CDQ.此时， AP × CQ = .

（2）将三角板DEF由图16所示的位置绕点O沿逆时针方向旋转，设旋转角为α.其中0° < α < 90°，画出图形并猜想AP × CQ的值是否改变？证明你的猜想.

5. 施教反思

修改过的方案试讲后又有一些想法：引入部分—三角板中的数学知识很多与本课重点联系不紧密，因此把知识梳理重点放在等腰直角三角形这个特殊三角形上，以它及其斜边上的高组成的图形为一个基本图形，为下文在复杂图形解决问题作铺垫. 基础练习及其变式也提炼出一张基本图形：两个直角顶点重合的直角三角形，根据同角的余角相等可以找到一对相等的角. 在上课过程中把基本图形画在黑板上，以及每个小题的不同解法相应的图形和辅助线都画在黑板上，给学生以参考、提示.

对问题的解决进行方法点拨：

（1）猜想从何而来？特殊情况

【探究一】中有两种特殊情况：一、△DEF的一条直角边经过B点（如图19、20）；二、△DEF的两条直角边分别与△ABC的两条直角边互相垂直（如图21）. 容易证明EQ = EP，因此大胆猜想一般情况下结论相同.

【探究二】中由于交点位置的限制只有一种特殊情况：△DEF的两条直角边分别与△ABC的两条直角边互相垂直（如图22）.这时容易证得■ = ■ = 2，因此可以猜想一般情况下结论相同.

（2）如何论证你的猜想？把一般情况转化成特殊情况

【探究一】需要证明线段相等，只需证明线段所在的三角形全等. 学生根据两种特殊情况，提出构造全等三角形的方法有两种.

（法一） 如图23，连接BE，转化成第一种特殊情况，构造出直角顶点重合的基本图形，根据基本图形可知∠PEB = ∠QEC，从而可证得△PEB ≌ △QEC.

（法二）如图24，作EM⊥AB于点M，EN⊥BC于点N，转化成第二种特殊情况，同样构造出直角顶点重合的基本图形，根据基本图形可知∠MEP = ∠NEQ，从而可证得△PEM ≌ △QEN. 两种方法各有一半左右的学生选用，思路很清楚.

【探究二】需要证明线段成比例，只需证明线段所在的三角形相似，绝大多数学生根据特殊情况提出方法一，极少数学生类比【探究一】提出方法二，只有唯一一名学生提出方法三.

（法一）如图25，作EM⊥AB于点M，EN⊥BC于点N，转化成图22的特殊情况，构造出直角顶点重合的基本图形，根据基本图形可知∠MEP = ∠NEQ，从而证得△PEM ∽ △QEN.

（法二）如图26，作EG⊥AC交AB于点G，构造直角顶点重合的基本图形，根据基本图形可知∠PEG = ∠QEC，从而可以证得△PEG ∽ △QEC.

（法三）如图27，在△ABC中以E为顶点构造∠AEG = ∠CEQ，可证得△AEG ∽ △CEQ，■ = ■.然后证明GE = PE，同样可以证得结论.

（3）根据【探究一】的三个小问，你可以概括出一个什么结论？

在旋转过程中，当直线DE交直线AB于点P，直线EF交直线BC 于点Q时，EQ = EP.

【探究三】是将前面的结论推广到更一般的情况，其中m的取值是有限制条件的，这个问题留给学生作为课后思考题. 小结：

【探究一】→【探究二】→【探究三】一连串的问题通过直角顶点E在AC边上的位置变化从特殊到一般，相应的结论从特殊的线段相等到一般的线段成比例，解决问题的方法也从特殊的三角形全等到一般的三角形相似，其中包含了重要的数学思想方法：从特殊到一般.

解决问题的基本思路：旋转过程中的特殊情况→得出猜想→论证猜想.

“试一试”让学生根据小结得出的基本思路自己独立去解决，其中第二题注重审题，在旋转过程中有两种不同情况需要分类讨论：如图28、29

学生在解决问题过程中出现了以下问题：①图形画错，原因主要有起始位置搞错或者旋转方向错，都属于审题不清；②相当一部分学生只画出了一种情况，简单的线段与线段相交（旋转角度小于45度时），属于考虑问题不全面. 对于学生出现的问题当场进行讲评. 指出这个问题的本质：在旋转过程中，始终保持△PAD ∽ △DCQ.

本课研究的解题思路同样适用于其他图形变换.