数学思想方法在数学课堂中的应用

姜瑞娥

教学是老师的教，学生的学的一个双边活动。老师的教直接影响到学生学习的效果，作为一名有远见的数学老师，绝不是让自己的学生整天埋头在题海中。而是要让我们的学生学的轻松、学的愉快，学得越来越聪慧。这就要求老师对教材完整的分析和研究，理清教材的体系和脉络，统揽教材全局，明确每一阶段的教学目标，教学要点。在知识的发生及运用中渗透数学思想方法，形成数学知识，方法和思想的一体化。

课堂上，一方面要注重基本功的落实，另一方面要注重思想方法的点拨。在课堂教学中应努力实现从过去的偏重知识技能的落实这单一的目标，转向体现“知识与技能、过程与方法、情感态度价值观”三维的课堂教学功能，做到知识技能、数学思考、解决问题、情感态度价值观多元整合，使数学课堂教学不再只是让学生获得必要的数学知识、技能，还要放眼未来，注重培养学生的数学思想方法、创新精神、实践能力，使学生在数学思维能力、解决问题能力、情感态度等方面充分发展，以便为学生的终身可持续发展打下基础。

在数学教学活动中，数学思想方法和数学知识是两个有机组成部分，数学知识是载体，我们应将数学思想方法有机的渗透在我们的课堂活动中。掌握了思想方法可产生和获得知识，而知识中又蕴藏着思想方法。因此，我们在教学中，强调知识的同时还得突出思想方法教学，从而加强学生数学认知结构形成的指导，让学生从中领悟学习数学的方法，学会学习。

数学思想方法的形成与应用是一项长期而艰巨的任务。因此，我们教师在平时的教学中，要不断的总结和归纳所学的数学思想和方法，在知识教学的同时，始终渗透必要的思想方法传授。对于七年级学生来说，才开始可能并不理解，但我们在教学中必须给学生通过例题形式归纳和总结这种思想和方法。让学生体会各种思想的精髓所在，为应用做好准备，为学会学习打下良好的基础。在这里，我将初中阶段几大数学思想及应用总结如下：

一、数形结合思想

在研究问题的过程中，由数思形、由形思数，把数和形结合起来，分析问题的思想方法。“数无形，少直观，形无数，难入微”。直观形象，激发学生的学习兴趣，人的思维是从具体到抽象，从而数形结合思想，有助于学生从形象思维向抽象思维转化的。

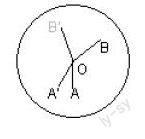
例1：某人晚上6时后外出时表上时针与分针的夹角是110°，晚上7时前回家时针表上时针与分针的夹角仍为110°，求此人外出了多少分钟？

分析：如图所示，假设OA、OB分别是此人外出时时针与分针的位置，OA′，OB′分别是此人回家时时针和分针的位置，则∠AOA′是时针转过的角，分针则从OB转到了OB′的位置，∠BOA+∠AOA′+∠A′O B′是分针转过的角，它们转过的角相差2×110°，借助方程这一数学模型，就可解决问题。

解：设这个人外出了x分钟，则时针转过了（0.5x）°，分针转过了（6x）°，由题意得 6x-0.5x=220 解得x=40

本题根据已知和所求之间的内在联系，既分析其数量关系，又揭示其图形的意义，并充分的利用这种结合，使问题得以解决。很好的考查了学生的观察能力，以及分析能力、解决问题能力。

在今后的数学学习中，要重视“数形结合”的思维训练，任何一道题，只要与“形”有关，就应该根据题意画出草图来分析一番。这样做，就会慢慢养成一种“数形结合”的好习惯。

二、整体思想

就是将局部放在整体中观察、分析，寻找整体与局部之间的联系，进而使问题的到简便解决的一种思想。

例2：将一个可自由转动的转盘平均分成5等份，分别标上数字1，2，3，4，5，自由转动转盘后，指针不指向数字3的可能性是多少？

分析：由于指针指向每个数字的机会都是均等的，若直接求指针不指向数字3的可能性，就是求指针指向数字1，2，3，4，5的可能性，显然比较繁琐。我们可以根据指针指向数字3和不指向数字3的可能性和为1，利用整体的思想来求就较为简单。

三、分类思想

当被研究的问题包含多种可能情况时，不能一概而论，必须按可能出现的所有情况来分别讨论，得出各种情况下相应的结论。这种处理问题的思维方法称为分类思想。比如，-a的正负问题，︱a︱等于多少的问题等等。

例3：若︱m-n︱=n-m，且︱m︱=4， ︱n︱=3，则（m+n）2=__________。

分析：由︱m-n︱=n-m，可知m-n<0，说明m比n小。

四、归纳思想

归纳就是从特殊、个别的事例推出一般规律的过程。归纳的过程就是创新的过程，这种方法常用于探索规律问题。

例如：

将你找的规律用代数式表示出来：___________________。

分析：观察比较已知算式中的数据，先横向观察：等号左边都是一個乘积加1，右边都是一个平方数，而且左边的乘积中的两个因数与右边的平方数中的底数是三个连续的整数，即左边是三个连续整数中较大数与较小数的积与1的和，右边是中间数的平方。在纵向观察：等号左边第一列是从1开始的连续整数直到，第二列数比第一列对应各数大2，第三列各数都为1.左边等于第一列乘以第二列加1.右边是一个数的平方，这数是左边第一列与第二列两个中间的整数。归纳这个规律可以表达为

数学应用，它不仅表现为一种工具，一种语言，而且是一种方法，是一种思维模式。课堂上重视数学思想的挖掘和渗透，是我们教学的核心任务。常见的数学思想除以上所述外还有许许多多，数学题目是无限的，但数学的思想和方法却是有限的。我们只要让学生学好有关的基础知识，掌握必要的数学思想和方法，学生就拿到了打开数学之门的金钥匙，就能独立地解决无限的题目，充分挖掘学生的智慧与潜力，真正体现教育的意义。