基于压缩多信号分类算法的森林区域极化SAR层析成像

张冰尘王万影*③毕 辉③赵 曜洪 文

①(微波成像技术重点实验室 北京 100190)

②(中国科学院电子学研究所 北京 100190)

③(中国科学院大学 北京 100190)

基于压缩多信号分类算法的森林区域极化SAR层析成像

张冰尘①②王万影*①②③毕 辉①②③赵 曜①②洪 文①②

①(微波成像技术重点实验室 北京 100190)

②(中国科学院电子学研究所 北京 100190)

③(中国科学院大学 北京 100190)

该文研究了一种基于压缩多信号分类算法的森林区域极化SAR层析成像方法。其具体步骤包括：全极化的SAR接收成像区域的反射回波，利用各极化通道的信号建立多观测向量模型；应用小波基对高程向结构进行稀疏表示，采用压缩多信号分类算法对观测区域的高程向后向散射系数进行重建，实现对森林区域层析成像。最后，通过仿真实验、PolSARpro仿真数据和德宇航E-SAR的P-波段数据验证了该方法在同等测量精度的要求下可以有效减少SAR层析成像所需的航过数，同时降低了虚假目标的出现概率。

极化SAR；层析；压缩多信号分类；小波基

1 引言

3D-SAR成像技术既继承了传统SAR系统所具备的全天时、全天候、高分辨率成像等优点，又避免了2维成像中处于同一散射单元内的目标散射点与雷达间斜距相等时存在的叠掩效应，能够将目标的高度向与距离向完全分离，实现对目标的3维分辨能力[1,2]。

SAR层析成像具有3维成像能力。SAR层析成像是沿垂直于视线的法线方向排列多个天线或利用同一天线在法线方向的不同轨迹高度对同一目标区域成像，来获得高度向上的分辨力。SAR层析成像技术不仅能够获得目标散射体的高程信息，同时还可以获得散射体在高度向上的分布，能完全恢复真实3维场景。SAR层析成像能够有效、快捷地实现3维成像，极大地扩大了SAR的应用范围，因此，已成为SAR技术发展的重要方向。SAR层析成像的方法包括谱估计和压缩感知，其中，压缩感知被广泛应用于雷达成像[3]。

1998年，德国宇航局(DLR)利用机载E-SAR系统进行了层析成像飞行试验，并采用傅里叶变换聚焦的算法成功实现3维成像。2000年，Reigber等人[4]提出了机载SAR层析模型，介绍了多基线SAR层析成像的原理，并采用频谱估计的方法实现了多基线L波段的层析成像。在SAR层析成像中，常用的谱估计算法有快速傅里叶变换(FFT)、多信号分类(MUSIC)以及CAPON等[5]。

传统的频谱估计方法信号序列长度受限，所能达到的高程向分辨率受限于高程向合成孔径的大小，所以高程向分辨率相对较低。为了解决这一问题，压缩感知的方法被应用于SAR层析成像[6,7]。压缩感知可以应用于SAR层析成像的前提是高程向的散射体分布是稀疏的，或者经过稀疏基处理之后满足稀疏性[8]。这种方法实现了高程向的超分辨率成像，然而仍然需要大量的航过来保证重建精度，这在实际实验中需要较高的成本。为了减少SAR层析成像所需的航过数提出了多信号的压缩感知处理方法[9,10]。

文献[11]提出了压缩多信号分类(CS-MUSIC)算法，该算法采用压缩感知的方法来识别部分支撑集，剩余的部分则利用一种广义的MUSIC算法进行恢复。该方法结合多观测向量实现对场景的重建，通过仿真实验证明该算法在保证恢复精度的同时，又可以大大地减少所需的航过数。本文结构如下，第2节给出森林区域SAR层析的多观测问题模型，通过小波基对森林区域场景进行稀疏化，并在后面的实验验证部分对实测P-波段数据结果进行多视处理；第3节介绍了CS-MUSIC算法的具体实施步骤；第4节利用仿真实验说明该算法应用于SAR层析成像中与其他算法相比的优越性；最后，第5节对全文进行总结。

2 信号模型

SAR层析成像的目的在于对同一目标场景在不同位置进行多次重复观测，以获得一个目标的多个投影，利用这些投影来计算物体的3维图像。SAR层析成像利用垂直于斜距方向的不同基线形成高程向的一个合成孔径，来获得在高程方向上合适的分辨率。

SAR层析成像沿着每一个轨道获得的回波信号都是一幅由方位-距离像素点组成的2维SAR图像，每一个像素点代表该方位-距离分辨单元内高程向所有目标点散射回波的叠加，表示如下[4]：

其中，a, r和v分别代表方位向、距离向和高程向，ym(a,r)为第m条基线处获得的2维SAR图像中位于(a,r)处的像素值，x(a,r,v)为高程向后向散射系数，λ为载波波长，r为观测点到场景中心的斜距，bm为第m条基线高程向高度。

对其进行高程向的离散化处理，得到SAR层析问题的数学模型，可表示为

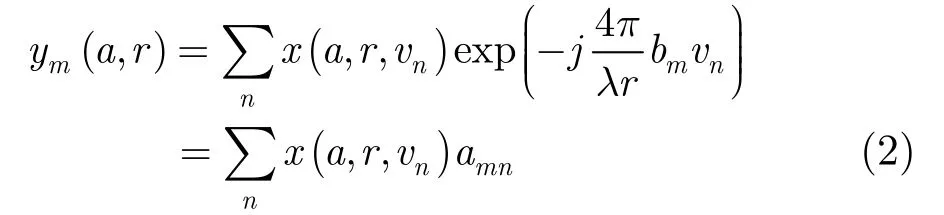
此时，对于有M次航过的SAR层析成像情况，我们可以用下面的矩阵相乘的形式来表示HH通道方位-距离分辨单元的回波采样向量，且。此时SAR层析成像数学模型可以表示为

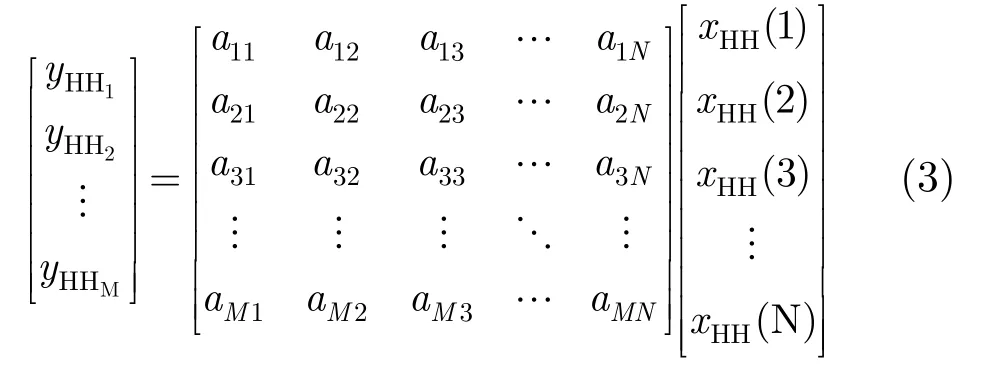
其中N为高程向网格数。我们称A为观测矩阵，单观测的SAR层析成像问题可以表示为

我们所要求解的是后向散射系数向量XHH，且XHH∈CN×1，即可获得高程向散射体分布情况。对于文中多极化信号的情况，回波信号由3个极化通道信号组成，此时回波采样矩阵，且满足X∈CN×3。此时，多信号SAR层析问题数学模型表示为

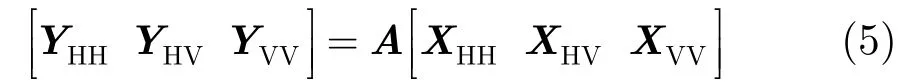
由于不同极化通道获得的回波信号具有一定的相关性，并且都是针对于同一目标场景，所以我们可以假设不同通道高程向后向散射系数均具有相同的支撑集[9]。

此时，我们所要解决的多信号压缩感知问题表示为

实际上，森林区域高程向一般并不具备稀疏性。所以在应用压缩感知的方法进行森林区域层析成像时，需要先将其在小波域进行稀疏表示[12]。这里令W∈CN×L代表小波基，α∈CL×3代表小波系数，则=XWα，此时，问题模型表示为

此时，观测矩阵表示为H=AW，通过多信号的正则化求解方法直接获得小波系数α，根据公式X=Wα，可以求得森林区域的后向散射系数。

这种多观测问题主要是求解具有相同支撑集的输入向量。目前，其求解方法分为两类，分别为阵列信号处理和压缩感知。然而，两种方法各有其局限性，所以本文采用结合了这两种方法的CS-MUSIC算法进行重建。

3 CS-MUSIC算法

传统的SAR层析成像是对同一场景进行重复观测，获得多幅2维复图像，每一幅复图像上的方位-距离像素点可视为本点高程向后向散射系数x(a,r,v)的傅里叶变换在某点的取值。若有多幅单视复图像，即有了x(a,r,v)的傅里叶变换在多点的取值，则可利用频谱估计的方法进行重建。

但是，传统的频谱估计方法信号序列长度受限，所能达到的高程向分辨率受限于高程向合成孔径的大小，所以高程向分辨率相对较低。如果要提高高程向分辨率就必须增加观测次数，来增加信号序列的长度，因此就需要多次的航过。

为了减少航过数，利用多极化通道信号之间的相关性，并引入了处理多观测向量(MMV)问题的CS-MUSIC算法。CS-MUSIC算法将所要求得的支撑集分为两部分，其中，k-3个支撑集元素用压缩感知的方法进行恢复，其余的3个元素通过一种广义的MUSIC准则求得。其具体步骤如下[11]：

(1)利用HH, HV以及VV通道的信号，构建多信号的像素点矩阵；

(2)确定像素点矩阵的列秩r =3，预估场景的稀疏度k，设置像素点矩阵和支撑集初值分别为

(3)利用同步的正交基追踪(SOMP)[13]算法求出k-3个场景支撑集的索引值，更新支撑集；其中，该步骤SOMP算法又可以分为以下子步骤：

(a)J次迭代之后，更新支撑集和残差信号

其中，I为单位矩阵，lj为第j次迭代求得的索引值，PSJ为回波信号在alj上的正交投影，为观测矩阵A的第lj列。

(b)选择1Jl+，满足

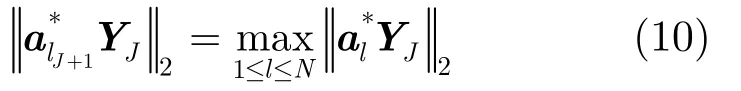
更新索引集，使

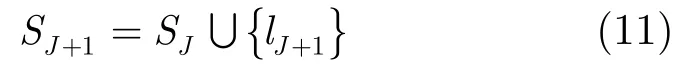
(c) 确定迭代终止条件，当J+1=k-3 时，终止迭代，并令Ik-3=SJ+1，否则，继续步骤(a)和(b) 。

(4)利用广义MUSIC算法估计出其余的3个支撑集元素，并将其与步骤(3)获得的支撑集进行合并，得到我们所需要的完整支撑集。其中，该步骤又可以分为以下子步骤：

(a)求得步骤(3)之后残差信号的自相关矩阵，根据目标点个数划分信号子空间U和噪声子空间Q；

(b)构造谱搜索函数

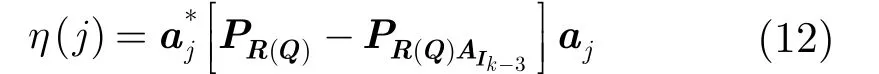
(c)将上一步搜索函数的结果进行升序排列，取前3个值对应的索引，并将其与Ik的元素一起放入S中，则S为我们所要求得的支撑集。

CS-MUSIC算法结合了压缩感知和谱估计两种方法，将支撑集分为两部分进行恢复，3k-个元素利用压缩感知的方法进行恢复，其余的3个元素则采用谱估计的方法获得。这种方法利用了压缩感知在欠采样的情况下可以进行精确恢复，同时也保证了MUSIC算法在已知目标个数情况下的精确重建，大大减少了虚假峰值的出现概率。

4 实验

以下通过仿真和真实数据实验来验证CS-MUSIC算法在森林区域极化SAR层析成像中的有效性和优越性。主要从两方面对算法性能进行评估：一是散射中心位置估计的准确性；二是减少航过数时高程向后向散射系数恢复情况以及虚假目标的出现概率。

4.1 仿真数据实验

根据文献[14,15]中介绍的森林场景体散射模型，给出森林区域在3个极化通道情况下的高程向能量分布情况，如图1所示

仿真数据实验1设计如下：选择不同极化通道情况下的散射模型，取高程向80 m范围内散射体分布，其散射中心分别在10 m和50 m处，分别代表地面和树冠散射中心，取10次航过，高程向均匀基线，基线间隔10 m，中心斜距5494 m，下视角45o，波长0.86 m，信噪比30 dB，选择Daubechies小波对高程向进行稀疏化处理。分别在航过数为10和6的情况下，将IST(迭代软阈值)[16]，MUSIC, CAPON[17]和CS-MUSIC算法的重建结果进行对比。

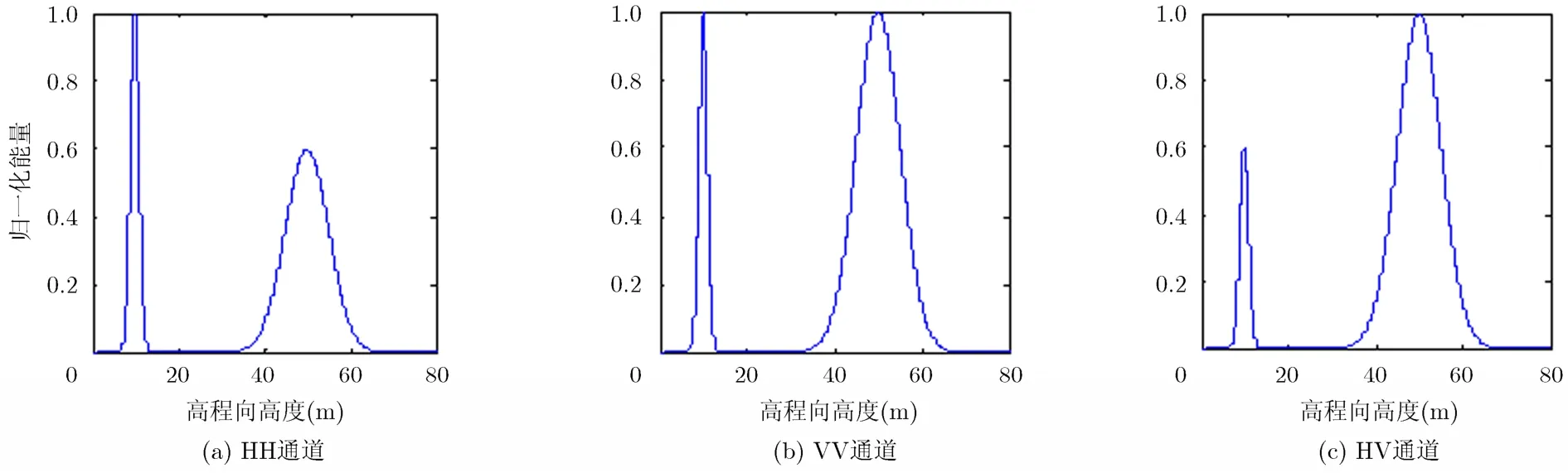
图1 3个极化通道高程向归一化能量分布

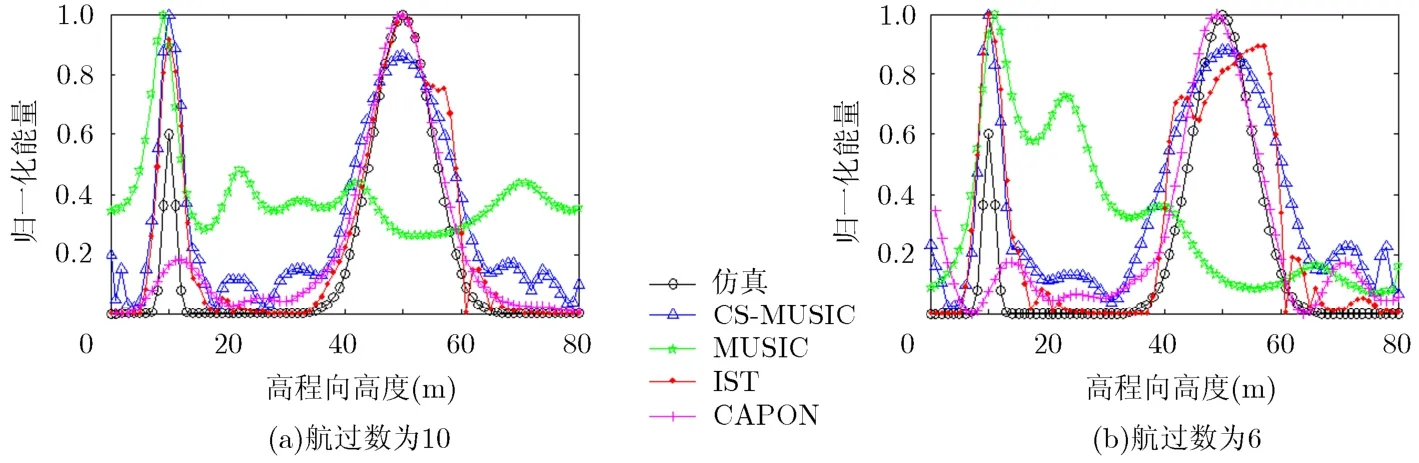
图2 不同航过数时各种算法获得的高程向后向散射能量分布与给定的仿真结果对比

仿真数据实验的结果表明，CS-MUSIC算法可以实现森林区域的SAR层析成像，在航过数为10时，IST, CAPON和CS-MUSIC算法都能准确的估计出10 m和50 m处散射中心的位置，并且树冠区域后向散射系数与仿真结果基本相符，而MUSIC算法只能估计出10 m处散射中心的位置，不能估计出另一处散射中心；当航过数减少为6时，IST和MUSIC算法均不能准确估计出两处散射中心位置，CAPON算法估计的散射中心位置发生偏移，并且估计的结果中出现很多虚假目标，干扰了对散射中心的判断，而CS-MUSIC算法在减少航过的情况下仍能准确地估计出两处散射中心的位置，并且后向散射系数变化趋势与仿真结果基本相符。

4.2 实测P-波段SAR数据实验

为了验证CS-MUSIC算法的有效性，我们使用了10组已聚焦和校正的P波段SAR图像数据，该数据是德国宇航局(DLR) 与瑞典国防研究局(Swedish Defence ResearchAgency, FOI)应用机载E-SAR 系统于 2007年 3 月到 5 月在瑞典Remingstorp 获取的，为欧空局(ESA)BioSAR 计划的一部分，称为 BioSAR 2007，主要树种为挪威云杉(Picea abies)，苏格兰红松(Pinus sylvestris)和桦树(Betula spp)，图3所示为该场景P-波段主影像的Pauli基。地形相对比较平坦，海拔从 120 m 到 145 m 之间，树高从 10 m 到 30 m。P-波段数据水平基线间隔大约为 10 m，水平总基线大约为 70 m，飞机多次观测几乎处于相同的高度。其他参数如下：飞行高度大约4005 m，空间分辨率斜距约为3 m，方位向为 1 m，入射角由近距的 25°到远距的 55°变化，中心频率为0.35 GHz。

图3 P-波段主影像 Pauli 基

我们选取了距离向800 m处的距离门包含的1800个方位向连续点，进行高程向的后向散射系数重建。从Pauli图中可以看到我们选择的实验区域(蓝色矩形框标注的距离门)以树木为主，对于验证CS-MUSIC算法在森林区域SAR层析成像中的应用具有代表性。实验中，IST算法和CS-MUSIC算法使用的小波仍然是消失矩为4的Daubechies小波，两组实验参数4种算法获得的实验结果，均进行窗口大小为64的方位向多视处理。如图4所示，在航过数为10时，CS-MUSIC算法与迭代软阈值(IST)算法、CAPON算法以及MUSIC算法高程向重建结果进行的对比。在航过数为10时，4种算法均可以将地面和树冠区域区分开，相比于MUSIC和CAPON算法，CS-MUSIC算法可以获得完整的地面信息，树冠信息更加完整，同时出现的虚假目标数目较少；与IST算法相比，CS-MUSIC算法很大程度上减少了虚假目标的出现概率。图5为航过数等于6时，CS-MUSIC算法与迭代软阈值(IST)算法，CAPON算法以及MUSIC算法高程向重建结果进行的对比。当航过数减少时，IST, MUSIC和CAPON算法已经不能找到地面和冠层的散射中心位置，并且出现很多虚假目标，这与前面的仿真结果一致。而CS-MUSIC算法仍然可以清晰地将地面与冠层区分开，并出现相对较少的虚假目标。

5 结束语

本文将CS-MUSIC算法应用于森林区域极化SAR层析成像，针对传统的SAR层析成像需要较多航过数的问题，提出了应用全极化SAR各极化通道信号之间的相关性构建回波观测向量矩阵，应用小波基对高程向结构进行稀疏表示，并采用多信号的CS-MUSIC算法进行高程向的后向散射系数重建，相比于常见的单信号SAR层析成像方法，该方法可以准确地估计出地表和树冠散射中心的位置，同时降低虚假目标出现概率，在同等重建精度的情况下，降低森林区域极化SAR层析成像时所需的航过数。

图4 航过数等于10时各种算法高程向重建结果(图示为50×1800的高程-方位向2维平面，对方位向进行平滑滤波的结果)

图5 航过数等于6时各种算法高程向重建结果(图示为50×1800的高程-方位向2维平面，对方位向进行平滑滤波的结果)

致谢 感谢中国林业科学研究院资源信息研究所陈尔学教授提供的Biomass数据集(龙计划项目第3期支持，ID10609)，帮助我们验证了算法的实用性。

[1] 张福博, 刘梅. 基于频域最小二乘APES 的非均匀多基线SAR 层析成像算法[J]. 电子与信息学报, 2012, 34(7): 1568-1573.

Zhang Fu-bo and Liu Mei. Uneven multi-baseline SAR tomography base on frequency domain least squares amplitude and phase estimation (APES)[J]. Journal of Electronics & Information Technology, 2012, 34(7): 1568-1573.

[2] 彭学明, 王彦平, 谭维贤, 等. 基于跨航向稀疏阵列的机载下视MIMO 3D-SAR三维成像算法[J]. 电子与信息学报, 2012, 34(4): 943-949.

Peng Xue-ming, Wang Yan-ping, Tan Wei-xian et al.. Airborne downward-looking MIMO 3D-SAR imaging algorithm based on cross-track thinned array[J]. Journal of Electronics & Information Technology, 2012, 34(4): 943-949.

[3] Zhang Bing-chen, Hong Wen, and Wu Yi-rong. Sparse microwave imaging: principles and applications[J]. SCIENCECHINA Information Sciences, 2012, 55(8): 1-33.

[4] Reigber A and Moreira A. First demonstration of airborne SAR tomography using multibaseline L-band data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(5): 2142-2152.

[5] Mariotti d’Alessandro M and Tebaldini S. Phenomenology of P-band scattering from a tropical forest through three-dimensional SAR tomography[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(3): 442-446.

[6] Zhu Xiao-xiang and Bamler R. Super-resolution power and robustness of compressive sensing for spectral estimation with application to spaceborne tomographic SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(1): 247-258.

[7] Budillon A, Evangelista A, and Schirinzi G. Three-dimensional SAR focusing from multipass signals using compressive sampling[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(1): 488-499.

[8] 王金峰, 皮亦鸣, 曹宗杰. 一种机载SAR 层析三维成像算法[J]. 电子与信息学报, 2010, 32(5): 1029-1033.

Wang Jin-feng, Pi Yi-ming, and Cao Zong-jie. An algorithm for airborne SAR tomography 3D imaging[J]. Journal of Electronics & Information Technology, 2010, 32(5): 1029-1033.

[9] Aguilera E, Nannini M, and Reigber A. Multisignal compressed sensing for polarimetric SAR tomography[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(5): 871-875.

[10] Aguilera E, Nannini M, and Reigber A. A data-adaptive compressed sensing approach to polarimetric SAR tomography of forested areas[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(3): 543-547.

[11] Kim J M, Lee O K, and Ye J C. Compressive MUSIC: revisiting the link between compressive sensing and array signal processing[J]. IEEE Transactions on Information Theory, 2012, 58(1): 278-301.

[12] Aguilera E, Nannini M, and Reigber A. Wavelet-based compressed sensing for SAR tomography of forested areas[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(12): 5283-5295.

[13] Tropp J A, Gilbert A C, and Strauss M J. Algorithms for simultaneous sparse approximation. Part I: Greedy pursuit[J]. Signal Processing, 2006, 86(3): 572-588.

[14] Treuhaft R N and Siqueria P. Vertical structure of vegetated land surfaces from interferometric and polarimetric radar[J]. Radio Science, 2000, 35(1): 141-177.

[15] Cloude S R and Papathanassiou K P. A 3-stage inversion process for polarimetric SAR interferometry[J]. IEE Proceedings-Radar, Sonar and Navigation, 2003, 150(3): 125-134.

[16] Daubechies I, Defriese M, and Mol C D. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint[J]. Communications on Pure and Applied Mathematics, 2004, 57(11): 1413-1457.

[17] Tebaldini S. Algebraic synthesis of forest scenarios from multibaseline PolInSAR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(12): 4132-4142.

张冰尘： 男，1973年生，研究员，主要研究方向为微波遥感与雷达技术、稀疏信号处理.

王万影： 女，1989年生，硕士生，研究方向为信号与信息处理、稀疏微波成像算法.

毕 辉： 男，1991年生，硕士生，研究方向为信号与信息处理、稀疏微波成像算法.

赵 曜： 男，1984年生，助理研究员，主要研究方向为信号与信息处理、稀疏微波成像算法.

洪 文： 女，1968年生，研究员，主要研究方向为合成孔径雷达成像与系统及其应用、极化/极化干涉合成孔径雷达数据处理及应用、3维微波成像新概念新体制新方法等.

Polarimetric SAR Tomography for Forested Areas Based on Compressive Multiple Signal Classification

Zhang Bing-chen①②Wang Wan-ying①②③Bi Hui①②③Zhao Yao①②Hong Wen①②

①(Science and Technology on Microwave Imaging Laboratory, Beijing 100190, China)
②(Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China)
③(University of Chinese Academy of Sciences, Beijing 100190, China)

This paper focuses on the polarimetric SAR tomography for forested areas based on compressive Multiple Signal Classification (MSC). First, full polarimetric SAR receives the reflected echo of the imaging area. Then, the signals from polarimetric channels are used to build multiple measurement vector model, and a wavelet basis is used in order to sparsely represent vertical structure. For achieving the measurement of forested area, the backscattering coefficients are reconstructed by Compressive Multiple Signal Classification (CMSC) algorithm. Simulated data from PolSARpro software and P-band data acquired by the E-SAR sensor of the German Aerospace Center validate that the method can effectively reduce the passes for SAR tomography and the probability of occurrence of spurious spikes under the same measurement accuracy.

Polarimetric SAR; Tomography; Compressive Multiple Signal Classification (CMSC); Wavelet basis

TN958

A

1009-5896(2015)03-0625-06

10.11999/JEIT140584

2014-05-06收到，2014-10-09改回

国家973计划项目(2010CB731905)和中国科学院创新团队国际合作伙伴计划“先进微波探测与信息处理”资助课题

*通信作者： 王万影 wangwanying0913@126.com