编组站作业计划自动执行功能研究

刘 欣，杨 扬，黄金成，罗 薇

（1. 西南交通大学 信息科学与技术学院，成都 610031；2.卡斯柯信号有限公司，上海 200071 ）

编组站作业计划自动执行功能研究

刘 欣1，杨 扬1，黄金成1，罗 薇2

（1. 西南交通大学 信息科学与技术学院，成都 610031；2.卡斯柯信号有限公司，上海 200071 ）

实现编组站作业计划的自动执行能力，核心在于实现编组站内各作业所需进路的自动优化选择，为每一项作业合理的安排走行进路及进路排序时机。本文以某编组站为背景，通过绝缘节和道岔节点，构建了车站网络的抽象描述方法。以作业准点率最大，作业总延误时间最小及进路总路径长度最短为优化目标，以进路冲突、作业时间冲突、满足作业计划要求等为约束条件建立了编组站进路选择的多目标优化模型。利用进路选择的0-1特性，提出了适合求解进路选择模型的遗传算法。实际案例证明：该模型可以较好地实现优化目标，有效调整进路在时间和空间上的相互干扰，实现了作业计划的自动执行功能。

编组站；作业计划；进路选择；遗传算法

编组站作业计划包括班计划、阶段计划和调车计划，在列车到站后对其进行到达、集结、解体、编组、出发等作业。按照编组站作业过程的不同，编组站办理的作业可分为改编货物列车作业（列车到达、解体、编组、出发），无改编中转列车作业（较简单只停留在到发场），货物作业车作业（取送车），机车整备和检修作业（机车出入段），车辆检修作业，其他辅助作业（摘挂列车作业等）。在进行编组站作业计划自动执行时，由于作业对象类型复杂繁多，根据作业过程对作业进行分类不利于作业进路的选定与优化。因此将编组站作业按照技术作业类型分为列车作业和调车作业：列车作业主要办理接发列车作业，到达作业、出发作业、通过列车作业；调车作业主要办理列车解体作业、编组作业、摘挂列车作业，取送车作业。

目前，国内外不少学者对车站作业计划的进路安排问题进行了深入研究，建立了优化模型，在求解模型时用了各种不同算法。周再玲等人研究技术站咽喉区道岔组的占用优化问题，分别确定每个子网的最小费用最大流，以此来选择进路[1]。史峰从有利于后续作业的进路排列出发，按序列化逐项作业排列进路的规则，分别提出了铁路车站咽喉区最大平行进路和最大概率进路的紧侧优化方法[2]。李莹慧通过对衔接点和锚点的定义，建立了车站网络的描述方法，从数学规划的角度建立了进路选择优化模型，采用免疫算法进行求解[3]。龙建成等人在李莹慧的基础上，定义了衔接点和承载点，在模拟退火算法的基础上采用复合优化算法进行模型的求解[4]。崔炳谋以各作业任务的延误时间加权值总和最小为最优目标，以任务的前后工序路径为动态约束，建立编组站进路调度数学模型，采用遗传算法进行求解[5]。吕红霞提出了基于道岔组的车站拓扑结构图的建立方法，并基于此模型运用最大最小蚂蚁系统设计了进路优化算法[6]。

研究发现，上述方法在求解列车进路安排问题时，车站现场错综复杂，不能简单地完全用数学模型描述，对于多目标优化模型，某些目标之间可能存在相互矛盾，在求解该问题时，对现有模型都进行了一定程度的简化，这便使得建立模型和实际要解决的实际之间存在一定差距。至今仍未形成一套系统的方法和理论体系，对于此类问题的求解目前仍处于探索阶段，因此，本文根据实际建立的模型对算法进行改进。

1 进路选择模型的建立

1.1 站场结构模型描述

李莹慧[3]与龙建成[4]等人将车站通过定义衔接点和锚点(承载点)，建立了车站网络图。车站设备道岔、轨道电路、绝缘节均能在图上体现，该种方法建立的车站拓扑图能够准确的反映车站结构，满足分段解锁的要求。但该描述方法对于大型编组站来说，站场结构描述过细，车站拓扑图上节点过多，导致在进路选排时，问题规模大，计算复杂度高。本文定义节点集合将信号机，轨道电路，道岔，绝缘节集中表示，结合站场型数据结构的左右设备连接关系表示站场网络图。定义如下抽象设备。

1.1.1 节点

以实际战场图（如图1）为例，图1中，X1表示进站信号机，D1，D2，…，D13表示调车信号机，将信号机、绝缘节、道岔与线路的交叉点、交叉渡线的交点定义为节点，由于信号机所在点均有绝缘节，故用信号机名表示此时的绝缘节，该处绝缘节用信号机名命名，抽象后如图2中的节点X1，节点集合抽象为绝缘节和道岔的节点集合。道岔与线路的交点用道岔名表示如节点1、3，道岔绝缘节节点用C1、C2、C3表示，交叉渡线的交点用m1表示，非信号机绝缘节用B1表示。

1.1.2 边

相邻两节点之间的线路定义为边，边的集合可以有效地表示进路的走行路径。相邻两绝缘节节点的边成为轨道区段如（X1，D1）。图1的抽象图如图2所示。

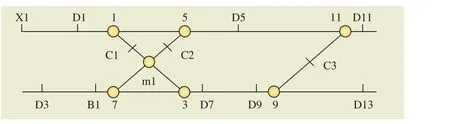
图2 站场网络拓扑图

1.2 变量定义符号说明

Nr，Er，Br分别表示进路r上节点的集合、边构成的集合、绝缘节构成的集合，P为需要安排进路的作业集合，|P|作业项数，作业P的可行进路集合为Rp，即进路表，进路数量为|Rp|，进路r的路径长度Dr，作业P的进路计划排列时间t0p，进路r起点到轨道绝缘节b的路径长度Drb，作业P的作业车长度Lp，作业P采用进路r占用轨道绝缘节b的时间长度tbp,r，作业P采用进路r从进路排列到进路占用结束的总时间tAp,r，作业P采用进路r进路占用的结束时刻tOp,r，作业P的准备时间，即实际占用与进路排列的时间差tcp，作业P的进路排列时刻tp假设车站进路都采用分段解锁，且进路各分段的解锁时间为0，进路开始排列时刻，作业车的中心处于进路起始点，进路一旦排列，进路上包括信号机、轨道电路、道岔等设备同时被占用，若为作业p分配进路r，则进路r上所有节点在同一时刻被占用，进路r上所有节点开始占用的时刻tkp为：

给定作业p∈P，进路r∈Rp，作业车在进路排列以后，于tkp时刻以平均速度vp依次通过进路上各节点, 当作业车尾部通过轨道电路绝缘节点b 时，进路进行分段解锁，得到：

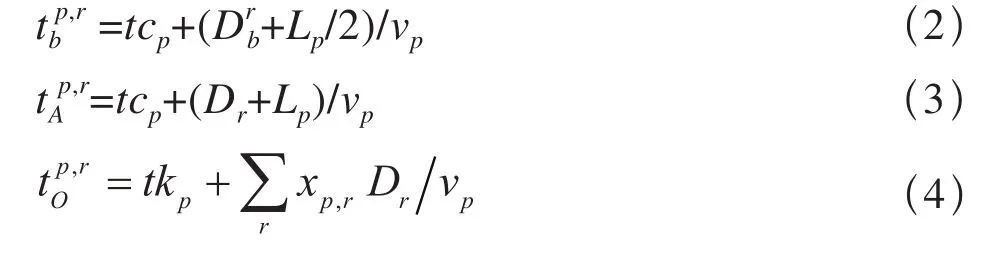
1.3 进路选择模型目标函数

编组站作业计划的自动执行必须要满足作业的准点完成，因此进路计划安排时段内，作业的总晚点时间最小，准点率最大为进路选择的总目标，该目标又直接由所选择进路的走行路径决定，因此将目标函数归纳如下：

作业准点率最大：

作业总延误时间最小：

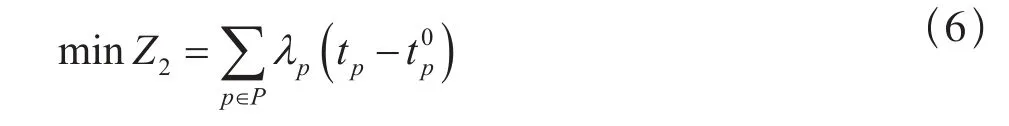
进路总占用时间最短：

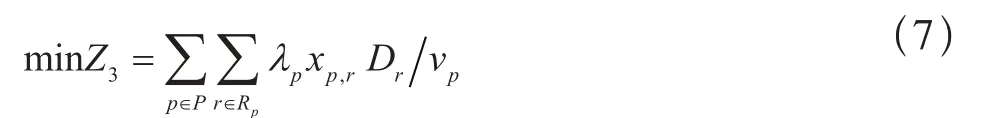
对目标函数进行归一化处理：

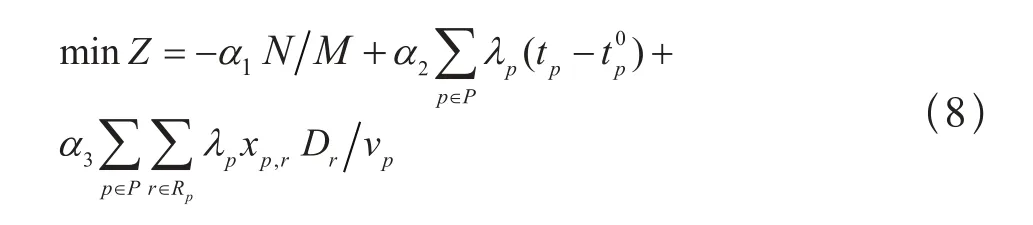
其中N为准点办理作业数，M为总的作业数， λp为每项作业p所对应的作业权重系数，将编组站作业分为列车作业和调车作业，优先保障列车作业的正点更为重要，其权重相对较大，式中α1, α2, α3为两目标函数的权重大小，α1＞α2＞α3，保证作业的准点更为重要 。

1.4 约束条件及说明

1.4.1 对每一项作业只能安排一条进路

xp,r为0-1变量，当作业p采用进路r时xp,r=1，否则xp,r=0

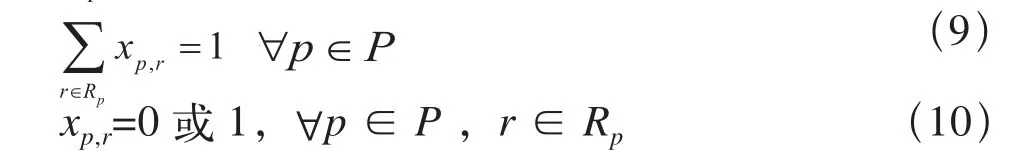
1.4.2 每一项作业的进路安排需要满足计划要求

1.4.3 两作业待安排进路在空间上存在交叉

需要在作业安排时间上进行疏解，以交叉渡线存在敌对进路的复杂情况为例，作业p1、p2分别采用进路r1、r2, Vr1, Vr2分别表示进路设备集合，φr1,r2为0–1变量，当进路有冲突时，即Vr1∩ Vr2≠φ，φr1,r2=1； 当进路无冲突时，Vr1∩Vr2≠φ，φr1,r2=0。为进路r1开始排列至p1的尾部通过绝缘节br1所需要的时间，如图3所示。

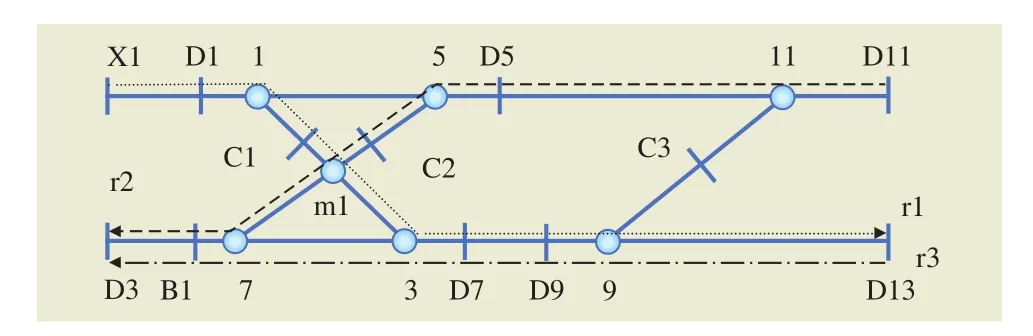
图3 冲突进路调整

进路r1的节点集合Vr1={X1--D1--1--C1--m1--3--D7--D9--9--D13}，进路r2的节点集合Vr2={D11-11--D5--5--C2--m1--7--B1–D3}，Vr1∩ Vr2={m1}，若进路r1先排列，则r2需要r1出清节点m1所在进路区段（C1，D7），即驶离后绝缘节D7，所用时间为，若进路r2先排列，则需要r2出清节点m1所在进路区段（C2，B1），即驶离后绝缘节B1，所用时间为，即满足关系如下：

或

设ξp1,p2为0-1变量，当tp1＜tp2时，ξp1,p2=1，ξp2,p1=0，否则ξp1,p2=0，ξp2,p1=1，取Q为足够大的正数，式（11）、式（12）等价于：

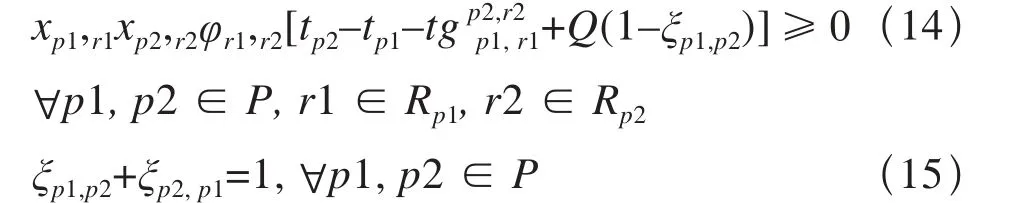
1.4.4 前后项作业间的关联

若作业p2需要在作业p1完成以后才能排列，则称作业p2是作业p1的后项作业，进路r1的最后两绝缘节间的边（轨道区段）是进路r2的第1个轨道区段，例如图2中的X1–D13（r1）和D13–D3（r3）即为前后项作业，两作业需要满足最小作业间隔时间为tmp1,p2则对任意p2是p1的后项作业有：

由式（15）、式（1）得：

1.4.5 作业p2是作业p1的后项作业

此时，若存在作业p，需要占用作业p1的终点，p2的起点时，则称作业p是作业p1，p2的相关作业，如图中若有作业p需要占用r1，r3的终端始端区段（D9，D13）时，p办理时机需要满足条件为p要么先于p1排列，要么后于p2出清共用设备时排列：

或者

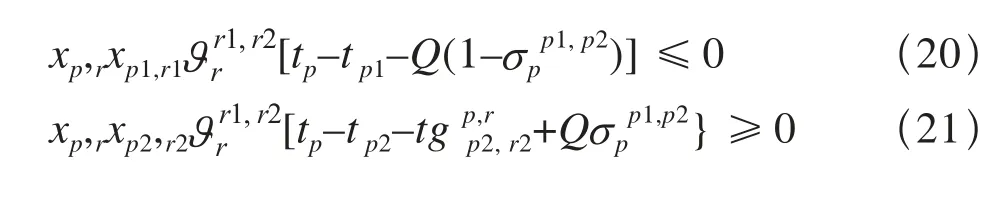
2 模型的求解算法

遗传算法在组合优化，自动控制领域有着广泛的应用，具有求解简单、快速、实用的特点。本文建立的模型是典型的多目标非线性优化问题，以上进路模型中，在给定进路选择x后，对应的进路排列时机可以直接由t=g(x)满足约束条件的线性规划模型决定，考虑到进路选择的0-1特性，采用二进制编码规则产生初始群体，具体流程如图4所示。

2.1 确定编码规则，产生初始种群

针对每项作业只安排一条进路的原则，将每一项作业的编码分成一个小模块，模块大小为|Rp|，共产生|P|个编码模块如下：

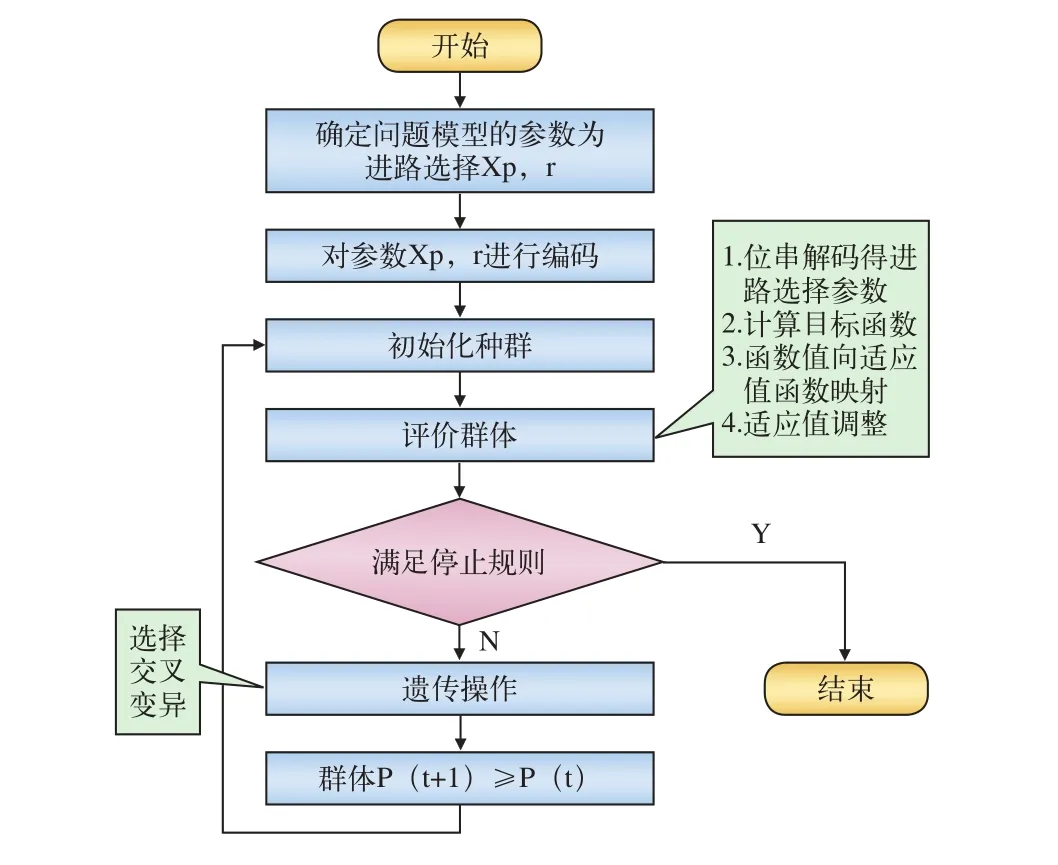
图4 遗传算法求解流程

|x1,1x1,2…x1,|R1||x2,1x2,2…x2,|R2||…|x|p|,1x|p|,2…x|p|Rp||，每一个符号“|”之间表示每项作业p的进路选择变量编码，表示一个编码模块，对于每个编码块用随机函数产生一个不超过其大小的正整数，将编码块中位数为此正整数的基因位定为1，而其他基因位为0，则产生了一个满足基本条件的个体，可以随机产生2M个个体，然后从中挑选较好的M个作为初始群体。

2.2 适应度函数的确定

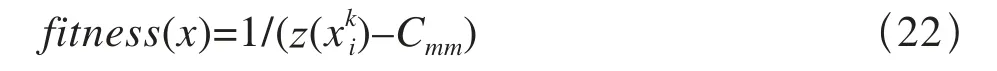
2.3 遗传操作

计算产生初始群体的每条染色体检查的适应值fitness，选择出适应值较大的前M个个体，然后进行交叉、变异操作，形成新一代种群。

2.4 终止规则

判断种群的适应度函数是否达到最优标准，或种群是否达到最大迭代次数，如果没有则返回2.3小节进行遗传操作，若达到则停止。

3 实例分析

以编组站到达场为例，根据作业参数表1，模型及算法参数设置如下：

α1=10, α2=5, α3=1种群规模NP=20，最大迭代次数NG=40，交叉概率PC=0.9，变异概率PM=0.04。

本例设计了4项作业用于验证模型的正确性，其中D21-3G是IG-D21的后项作业，作业时间间隔为2 min，IG-D21与4G-XQ时间、空间上有冲突，属于敌对进路，采用设计的算法得到最优进路选择方案及进路排列时机如表2所示，此时列车的准点率到达了100%。

图5中的进路安排结果表明，由于XN-IIG，4G-XQ属于列车作业应优先安排，考虑作业时间相近，通过模型求解安排了两条平行进路，受发车作业4G-XQ的影响，调车作业IG-D21时间上进行了调整，安排了进路交叉最少的r3，D21-3G是IG-D21的后项作业，受前项作业延误影响，后项作业也作出相应的时间调整，本模型可以优化调整进路的排列时机和排列次序。

表1 作业参数表

表2 作业排列时机安排

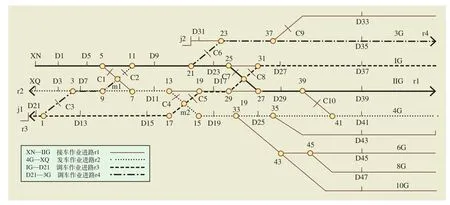
图5 进路走行方案

4 结束语

编组站作业计划的自动执行主要在于为每项作业计划选择最优的走行路径及排列时机。本文以编组站到达场为例，将作业计划根据权重系数不同简化为列车和调车作业，通过构建车站网络的平面拓扑结构将问题抽象为一个0-1选择的多目标优化模型，通过遗传算法可以有效的求解进路优化模型，获得较高的列车准点率。通过验证，该算法避免了进路在空间和时间上的交叉，正确、有效地实现了多项作业计划的自动执行功能。

[1]周再玲，游 斌，李雪婷.铁路技术站咽喉区道岔组占用安排的模型和算法[J].四川工业学院学报，2002，21（3）.

[2]史峰，谢楚农，于桂芳. 铁路车站咽喉区进路排列优化方法[J].铁道学报，2004，26 （4）.

[3]李莹慧. 铁路车站进路选择的免疫进化算法研究[D]．北京：北京交通大学，2006．

[4]龙建成，高自友，马建军，等. 铁路车站进路选择优化模型及求解算法的研究[J]. 铁道学报，2007（5）.

[5]崔炳谋，马钧培，张 朴.编组站进路调度优化算法[J].中国铁道科学，2007(2).

[6]吕红霞. 铁路大型客运站作业计划智能编制的优化技术和方法研究[D].成都：西南交通大学，2008.

[7]杨 扬.车站信号控制系统[M].成都：西南交通大学出版社，2012.

[8]吕红霞,陈 韬，张 杰.铁路大型客运站运转作业优化理论及系统设计[M].成都：西南交通大学出版社，2011.

[9]吴海辉.基于遗传算法的铁路编组站阶段计划编制研究[D].南昌：华东交通大学，2009.

[10]陈 鹏.遗传算法的改进及在调度优化中的应用[D].北京：中国地质大学，2011.

[11]北京全路通信信号设计院.成都北编组站综合集成自动化系统CIPS需求分析说明书[Z]. 2004.

责任编辑 陈 蓉

Automatic execution function of marshalling station operation plan

LIU Xin1, YANG Yang1, HUANG Jincheng1, LUO Wei2
( 1. School of Information Sciences and Technology, Southwest Jiaotong University, Chendu 610031, China; 2. Kasco Signal Company Limited, Shanghai 200071, China )

To implement the function of marshalling station operation plan automatically, the key point was to implement the automatic optimization of needed route of marshalling station, s every operation, arrange the running route of every operation in stations and the route setting time reasonably.This paper was based on a marshalling station. By def i ning the insulated joints and switch points, the abstract description method of station was constructed. Punctuality rate maximum and total delay time reasonably minimum of operation as well as total route traveling length shortest were taken as optimization targets. To establish the marshalling station route choice of the multi-objective optimization model, route conf i lict，operation time conf l ict, operating planning requirements should be considered as constraint conditions. Considering 0-1 characteristics of route choice, the paper proposed Genetic Algorithm which was suitable for solving the route choice model. The actual case proved that the model could implement the two goals, avoiding mutual interference of route in time and inter space effectively, implementing the automatic execution function of marshalling station operation plan.

marshalling station; operation plan; route choice; Genetic Algorithm

U291.4∶TP39

A

1005-8451（2015）10-0014-05

2015-01-25

中国铁路总公司科技研究计划项目（2013X012-A-1，2013X012-A-2，2014X008-A）

刘 欣，在读硕士研究生；杨 扬，副教授。