基于PID算法ATO系统的仿真研究

王先明，陈荣武，蔡哲扬

（西南交通大学 信息科学与技术学院，成都 610031）

基于PID算法ATO系统的仿真研究

王先明，陈荣武，蔡哲扬

（西南交通大学 信息科学与技术学院，成都 610031）

基于现有列车运动模型，设计了列车速度闭环仿真模型，其中控制器采用PID控制算法，当系统输入波浪形V-S曲线时，在PID控制器控制参数设置恰当的情况下，系统输出的V-S曲线具有较为满意的跟随性，在输出的加速度曲线中在列车的启动阶段和中间速度波动阶段会有尖峰波动现象。针对基于PID控制算法的ATO系统出现的问题进行了分析。

城市轨道交通；ATO系统；PID控制；仿真

ATO控制城轨列车自动运行的主要目的是模拟司机在最佳状态下的驾驶，实现一般情况下的高质量的自动驾驶，从而提高列车的运行效率，改善列车运行的舒适度和节约能源。寻找适合ATO系统的算法，并且研究出科学、成熟的ATO系统是行业进步的关键点之一。

本文重点分析了ATO系统的功能，基于现有列车运动模型，设计了列车速度闭环仿真模型，其中控制器采用PID控制算法，针对基于PID控制算法的ATO系统出现的问题进行了分析。

1 列车自动运行系统的研究

列车自动驾驶（Automatic Train Operation, ATO）系统是列车自动控制系统（Automatic Train Control，ATC）的子系统，它与列车自动监督（Automatic Train Supenvsion, ATS）子系统、列车自动防护（Automatic Train Protection，ATP）子系统协调合作，共同完成列车的自动控制。

ATO系统接收来自ATS发送的目的地编码、运行时分等信息，并且接收来自ATP发送的当前列车速度、加速度，目标速度，当前位置等信息，跟随ATP生成的速度-距离曲线，在ATP的防护下安全运行，实现列车的自动驾驶。

2 PID控制算法的研究

PID控制算法是基于偏差在过去、现在和将来做出调节量估计的一种简单而有效的控制算法。PID控制算法被广泛地应用在许多工业控制当中，采用PID控制理论来实现地铁列车的速度控制也应运而生。

传统PID控制系统结构如图1所示。

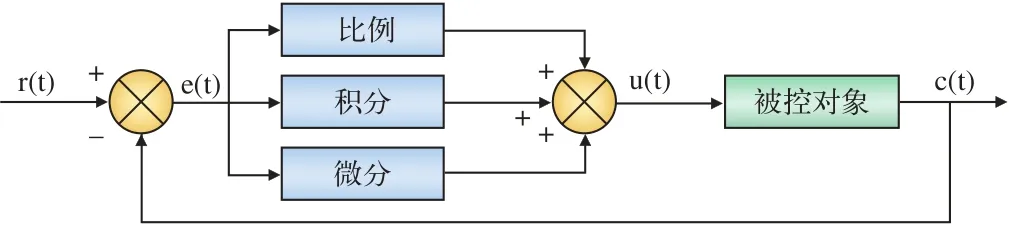
图1 PID控制系统结构图

传统PID控制系统主要由PID控制器和被控对象组成。PID控制部分又由比例（P）、积分（I）和微分（D）3个环节构成，该控制器具有传递函数：

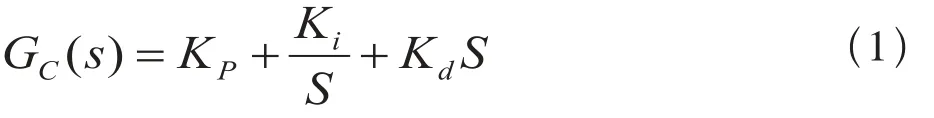
3 PID控制算法在ATO系统上的应用

在控制理论中，PID控制器是一种非常经典且常用的控制器，它使用简单、方便，而且通常能够获得较好的控制效果。

闭环PID控制系统的系统原理图如图2所示。

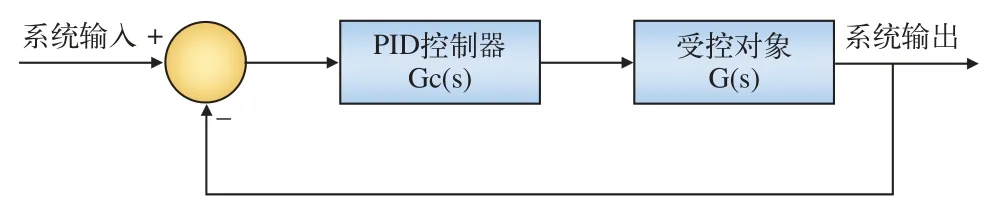
图2 闭环PID控制系统原理图

根据参考文献[7]，得到列车目标系统的传递函数形式为：

参考昆明地铁线路在设计时候的标准，假设系统的调整时间为11 s≤t s≤15 s，系统超调时间不超过10%。根据图2闭环PID控制系统原理图，得出系统的闭环传递函数为：

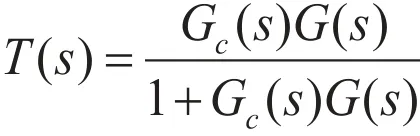
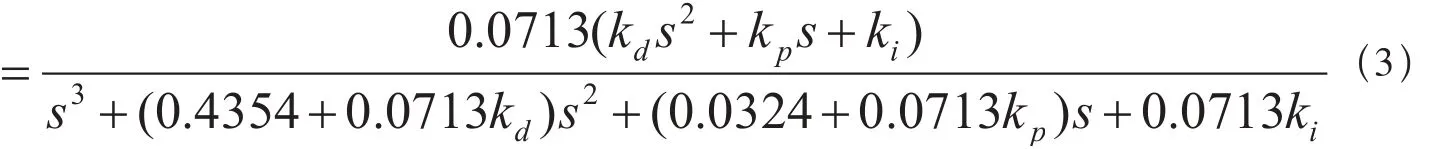
[9]可知，对于一个三阶系统，只要主导极点的实部小于第3个根的实部的1/10，三阶系统的响应就可以用二阶系统的主导极点近似表示。因此，通过极点配置，将该系统降为二阶系统来考虑。假设第3个极点为r3=–a，可以得到KP=6.9056a，Ki=0.454a，Kd=14a。将这3个参数作为PID控制器的参数时，系统的零极点将会相消，最后简化为一阶系统，取a=0.36，得到KP=2.49，Ki=0.16，Kd=5.04。

根据这3项参数，利用MATLAB软件建立仿真模型，如图3所示。

图3 MATLAB simulink仿真测试图

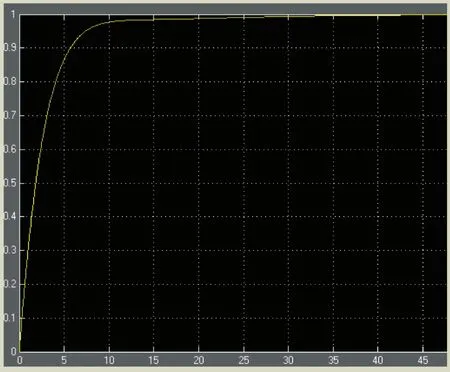
图4 阶跃响应曲线图

从图4的图像中可以看出，调整参数之后的系统阶跃响应，超调量基本上为零，调整时间ts也约等于14 s，基本达到了设计要求。

4 ATO系统仿真及分析

本节将对上文得到的列车运行模型和系统PID控制参数利用Matlab软件进行相应系统的设计。

4.1 ATP曲线的生成

参考昆明地铁线路的数据生成V-S曲线，如图5所示。

4.2 simulink仿真模型

设计出仿真模型，如图6所示。考虑到线性系统的叠加特性，将线路中坡度、弯道对列车运行的影响也考虑进去，作为对系统的干扰加到控制回路当中。4.3 ATO系统仿真结果

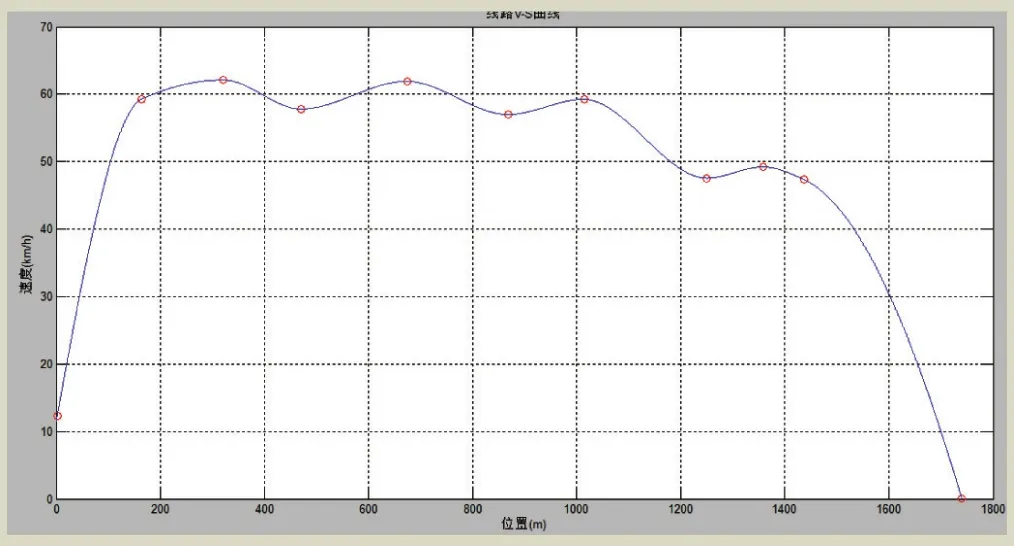
图5 列车V-S曲线

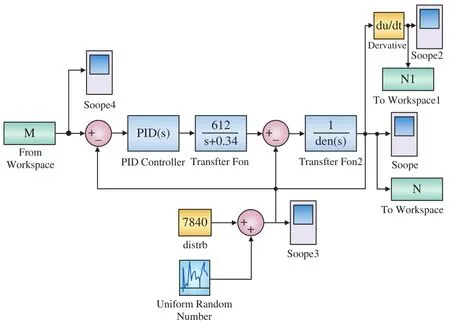
图6 simulink仿真模型

基于昆明地铁线路，在PID控制下得到的列车在依次经过牵引-惰行-制动阶段得到的速度-位置曲线和加速度-位置曲线如图7和图8所示。

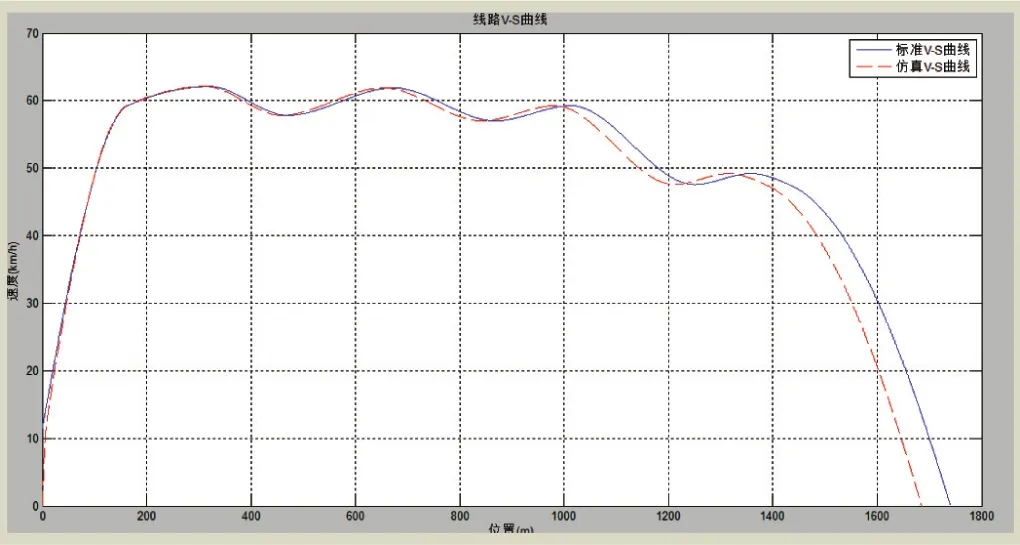
图7 经过牵引-惰行-制动阶段速度-位置曲线图

图8 经过牵引-惰行-制动阶段加速度-位置曲线图

4.4 ATO设计系统仿真结果分析

从图7和图8可以看出，在列车的启动阶段，目标初始速度不为零，实际情况下列车速度要从零开始启动加速，所以相应会出现一段时间的速度延时情况。列车实际运行速度相对于目标运行速度出现了偏差，但是速度偏差还是在允许的范围内。但在列车的最后制动停车阶段，速度偏差逐渐增大，最后实际的定位停车误差大约为50 m，明显不符合要求。因此，有必要对该初步设计的系统进行相应的改进和优化。

4.5 ATO仿真系统的改进和分析

改进的主要对象是列车最终的稳态误差，经过分析，考虑在系统的前面添加一个前置滤波环节。引入具有零点的校正装置来调整闭环传递函数极点位置的同时，消除引入到闭环传递函数中的零点的影响。 现在需要确定的是前置滤波模块的具体参数。

没有添加前置滤波模块的系统的闭环传递函数表达式为：

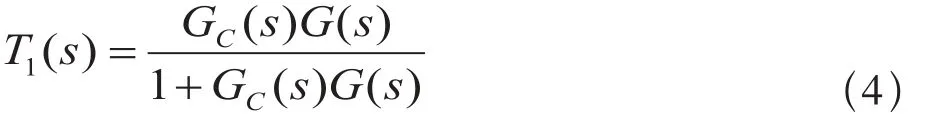
将具体参数带入，最后化简后得到：

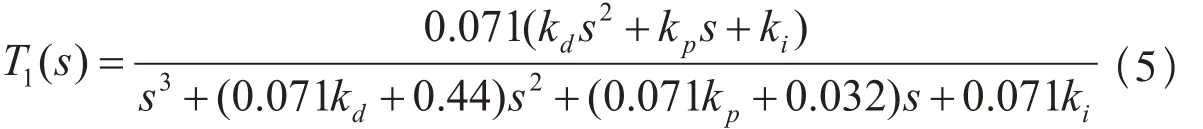
ITAE是系统设计的一个重要的性能指标，基于ITAE准则，T(s)对于阶跃输入的最优系数为：

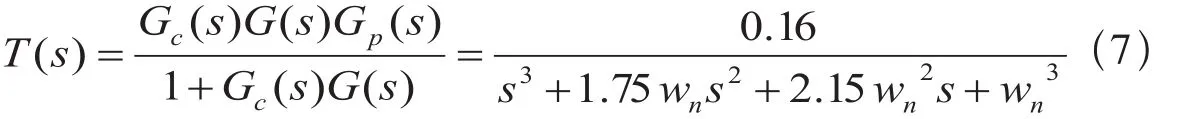
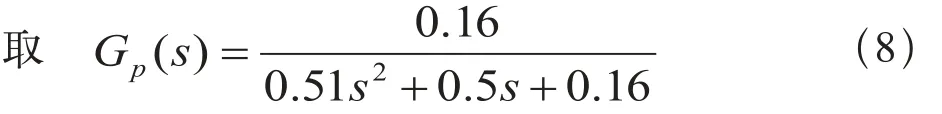
改进后系统的设计，如图9所示。

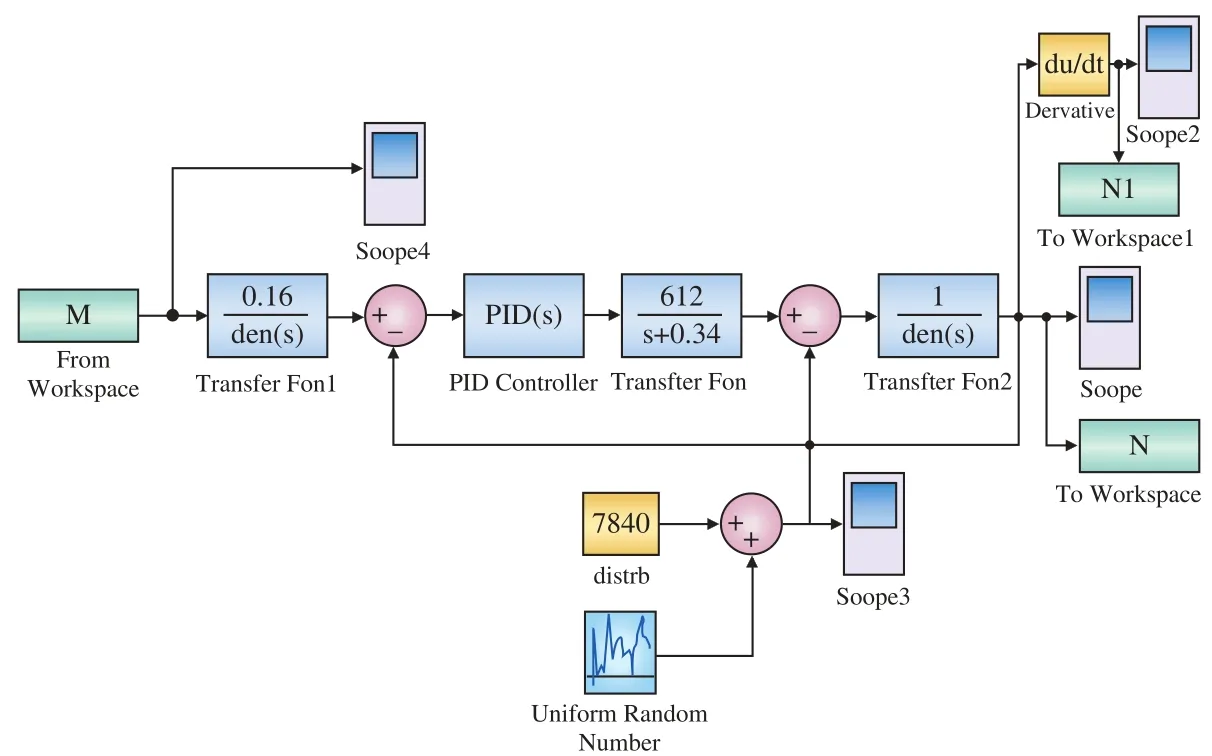
图9 改进系统设计图

改进之后导入列车经过牵引-惰行-制动阶段的线路数据，得到如图10和图11所示的仿真图像。

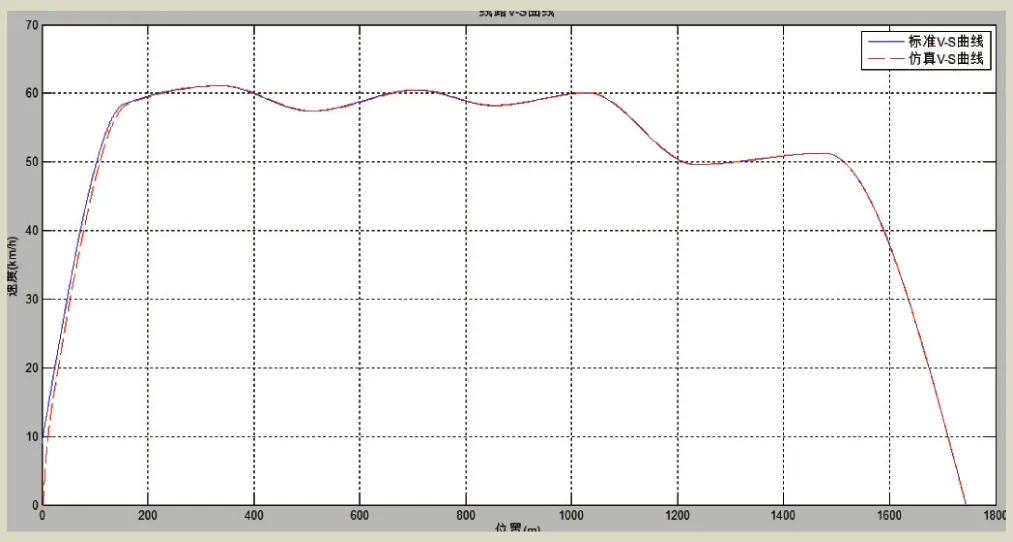
图10 改进系统经过牵引-惰行-制动阶段速度-位置曲线

图11 改进系统经过牵引-惰行-制动阶段加速度-位置曲线图

从图10中看到原系统经过添加前置滤波模块之后，列车在经过牵引-惰行-制动阶段的速度跟随性效果有了显著提高，相比于原系统，列车在后面惰行-制动阶段列车实际速度与参考速度的速度差有了很大减少，最后列车的对位停车的误差也缩小到了要求的±25 cm之内，解决了原来系统出现的停车误差较大的问题，同时在图11看到，列车在启动阶段加速度仍然有稍微大的波动，虽然列车启动延时是无法消除的，但是在行驶中途和制动阶段的加速度变化量是在可以接受的范围内。

5 结束语

本文以城市轨道交通ATO系统为背景，着重研究了ATO系统的性能指标和控制算法，并且设计了仿真系统，对相应数据进行了仿真测试和分析，以此来判断ATO算法的可行性。

参考文献:

[1]唐 涛，黄良骥. 列车自动驾驶系统控制算法综述[J].铁道学报，2003，25（2）：100.

[2]毛保华. 列车运行计算与设计[M]. 北京：人民交通出版社，2008，1.

[3]金奇，邓志杰. PID控制理论及参数整定方法[J].重庆工学院学报，2008，22（5）：91-94.

[4]安志强. ATO 目标速度曲线优化及跟随控制研究[D]. 成都：西南交通大学, 2011.

[5]姚 理. 基于智能控制算法的列车自动驾驶系统的优化研究[D]. 北京：北京交通大学, 2009.

[6]彭其渊, 石红国, 魏德勇. 城市轨道交通列车牵引计算[M].成都：西南交通大学出版社, 2005.

[7]王洪坡. 磁悬浮列车速度控制与自动驾驶系统研究[D]. 长沙：中国人民解放军国防科学技术大学, 2002.

[8]吴玉生. 磁浮列车自动驾驶 (ATO) 系统控制算法研究与仿真[D]. 长沙：中国人民解放军国防科学技术大学, 2005.

[9]多尔夫, 毕晓普, 赵千川, 等. 现代控制系统[M]. 北京：清华大学出版社, 2008.

[10]任晓莉. 城轨列车ATO 性能指标确权算法研究[D]. 成都：西南交通大学, 2012.

责任编辑 徐侃春

Simulation research on ATO System based on PID Algorithm

WANG Xianming, CHEN Rongwu, CAI Zheyang
( School of Information Science & Technology, Southwest Jiaotong University, Chengdu 610031, China )

Urban Transit; Automatic Train Operation System; PID control; simulation

U284.482∶TP39

A

1005-8451（2015）04-0044-04

2014-09-18

王先明，在读硕士研究生；陈荣武，高级工程师 。

Abstrac:The thesis reviewed the development of the Automatic Train Operation(ATO) System and designed the train speed closed-loop simulation model, in which the PID Algorithm was used, when the V-S curve was input to the System in the PID controller, the output was satisfactory followed the start-up phase of the train. During the intermediate speed fl uctuation stage, there would be a spike wave phenomena in the output of the acceleration curve. Problems of ATO System based on PID Algorithm was analyzed.