基于MapReduce的时序数据离群点挖掘算法

刘 峰，延婉梅，李洪人

（1.北京交通大学 计算机与信息技术学院，北京 100044；2.朔黄铁路发展有限公司 原平分公司，忻州 034100）

基于MapReduce的时序数据离群点挖掘算法

刘 峰1，延婉梅1，李洪人2

（1.北京交通大学 计算机与信息技术学院，北京 100044；2.朔黄铁路发展有限公司 原平分公司，忻州 034100）

针对海量数据中离群点的挖掘，将网格聚类和MapReduce编程模型相结合，排除不可能包含离群点的网格，再用LOF算法对剩余网格中的数据进行离群点检测。为了提高网格聚类的检测精度，本文提出了一种基于聚类半径的改进算法。实验表明了该算法的有效性，同时分析了在节点数不同的情况下，网格聚类所用时间，证明了基于MapReduce的网格聚类适合处理海量时序数据。

海量时序数据；网格聚类；MapReduce；LOF；聚类半径

多变量时间序列（MTS）在各个领域中是非常普遍的，比如动车组数据。动车组在运行过程中接收到的闸片数据可以用多个变量的MTS描述，MTS矩阵通常用m•n矩阵来表示，其中m是记录的个数，n是属性的个数。

在分析时间序列时，经常会发现一些特殊的数据或数据段，它们的波动显著不同，这种极少出现的数据点或者数据段就称为异常点[1]。异常点的出现严重影响了数据利用的效率和决策质量，同时，时序数据中的离群数据使人们能够发现一些潜在有用的知识，如动车运行中环境因素对闸片的影响。

目前异常检测方法主要包括以下几种[2]：基于统计的孤立点检测方法；基于距离的孤立点检测方法；基于密度的孤立点检测方法；基于聚类的方法[3]。

针对单变量时间序列，基于离群指数[4]和基于小波变换[5]的异常数据的挖掘方法得到了应用。针对多变量时间序列，有学者提出了基于滑动窗口[6]和基于局部线性映射[7]的异常数据诊断方法。然而，随着各种数据的急速增长，目前，对如何从海量的多变量时间序列中挖掘出异常数据这方面的研究很少。

本文在此基础上对时序数据的异常值进行检测，将MapReduce与网格聚类相结合，利用基于网格的聚类对数据进行划分，有助于快速发现可能的离群点，快速找到可能离群点的k-近邻。同时对基于网格的聚类进行改进，提高检测精度。最后以动车组闸片数据验证了算法的有效性和合理性。

1 MapReduce简介

MapReduce编程模型的原理是[8]：利用一个输入key/value对集合来产生一个输出的key/value对集合。用户可以用两个函数表达这一计算：Map（映射）和Reduce（规约）函数。MapReduce将大数据集分解为成百上千的小数据集，每个（或若干个）数据集分别由集群中的1个节点并行执行Map计算任务，并生成中间结果，然后这些中间结果又由大量的节点并行执行Reduce计算任务，形成最终结果。

为了适合MapReduce计算模型，数据记录都是以行形式存储的。将网格聚类和MapReduce编程模型相结合，程序可以在Map阶段读入网格划分数据，然后并行处理每行数据，各个节点分别进行计算，能够提高效率。

2 网格聚类

基于离群指数的离群点检测中，算法的时间复杂度主要集中在查找一个点的k个邻居，同时，当数据海量时，频繁地遍历数据集合会消耗很多的时间，因此，很可能会出现机器内存不足，不能完成任务的情况。所以，本文引入网格聚类的方法。基于网格划分的离群点检测方法是离群点挖掘的一种非常重要技术，该方法的核心思想：先将数据空间的每一维进行划分，原数据空间被分割成彼此不相交的网格单元，距离较近的点归属于同一个网格的可能性比较大，快速地查找一个点的k个邻居。同时，由于离群点的数目只占整个数据集的一小部分，因此在计算LOF 值之前，把不可能成为离群点的点集提前删除，然后对剩下的点集作进一步检测，选出符合条件的点作为结果[9]。该算法的优点是：采用聚类方法把非离群点集筛选出来删除掉，再对剩下的可能成为离群点的点集做进一步考察，减少了不必要的计算，节省了算法的运行时间。

2.1 网格密度定义

在网格数据结构中，由一般的方法是指定一个数值δ于每个网格单元都有相同的体积，因此网格单元中数据点密度的计算可以转换成简单的数据点个数，即落到某个单元中点的个数当成这个单元的密度[9]。一般的方法是指定一个数值δ，当某网格单元中点的个数大于该数值时，就说这个单元是密集的。

2.2 网格的划分

在基于网格划分的聚类分析与离群点检查中，如何确定网格单元格划分的方法是问题的关键。最常用也是最简单的一种划分方法是将每个维度做等距离划分。例如，在对d维数据空间进行网格划分时，每一维度的距离为k，划分后所得到的网格单元数为。

2.3 相邻网格单元定义

该定义表明，两个网格相邻当且仅当这两个网格单元有一个公共的边或面。

2.4 网格编号

对网格编号：首先保证d维属性的顺序固定A1，A2，…，Ad，对于其中的每个属性Ai（1≤i≤d），将其均分为s个间隔段，按照范围从小到大编号为1，2，…，s。那么一个网格的编号即为Ai（1≤i≤d）中范围编号的集合。之所以这样定义网格编号，是为了方便查找一个网格的邻居网格，假设一个网格的编号为那么一个网格的邻居网格编号为

3 Mapreduce实现网格聚类

3.1 Map函数与Reduce函数的基本思想

Map函数的任务是判断每条记录属于哪个网格，网格的划分都是提前定义好的，生成的网格范围存储到hashMap中。那么，hashMap的key值为当前网格的编号gridNumber，value值为网格范围rangeneighbor。Map函数的输入是各条记录数据，输出为各个记录所属的网格编号。伪代码如下：

HashMap(gridNumber,range);//网格范围都存储在HashMap中

For each data p//对数据集中的每条记录p

For each gridNumber //循环遍历每一个网格的范围

compare(p, range);//比较p和每个网格的范围

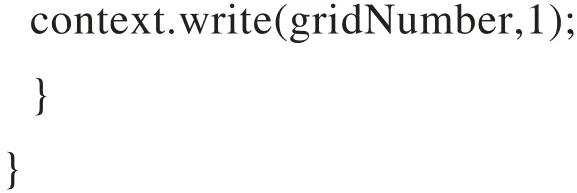
Reduce函数的任务是筛选出网格密度最小的n个网格，伪代码如下。

sum+=1;//计算每个网格中的数据个数

hashMap1.add(gridNumber,sum);//将计算后的数值存储到hashMap1中

sort();//根据sum值升序排列

Iterator iter = map.entrySet().iterator();

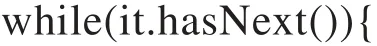
for i from 0 to n-1//循环遍历hashMap它的前n个数，即为网格密度最小的n个网格

上述过程是一般的网格聚类方法，但是网格的划分与划分间隔大小的选择直接影响着算法的正确性与算法的执行效率。如果间隔 w 选择过大，则会导致一个含有离群点的网格单元的相邻单元都不为空，该单元作为非边界网格单元被删除，其离群点不能被检测到，从而引起有用数据的丢失；如果 w选择过小，网格单元的计算量会大大增加；可能导致比较稀疏的聚类点不容易被检测到，这样就会增加后面 LOF 的计算工作。因此，合理地划分每一维是算法的关键所在，也是本文的研究重点。

同时，利用网格中数据点的个数作为网格密度的标准是不严谨的，如果一个网格中数据点分布的较为集中，不管数据点的个数是多少，这些数据是离群点的可能性都较小。相反，如果一个网格中数据点的个数较多，但是数据分布的特别分散，那么这些数据点是离群点的可能性也是较大的。

3.2 基于聚类半径的改进算法

本文提出一种改进方法，可以减小网格划分的影响，对于每个网格内的数据密度，不单纯使用数据个数的方法，而是通过网格质心与网格内最远点的距离来衡量，即聚类半径。规定网格质点为所有数据点的平均值。直观的想法是聚类半径大的数据分布的较为稀疏，聚类半径小的数据分布的较为密集。

那么在Map阶段，输出的value值不能只是计数的，因为在reduce阶段求质心时需要数据值，相应的Map阶段的伪代码为：

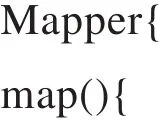
HashMap(gridNumber,range);//网格范围都存储在HashMap中

For each data p//对数据集中的每条记录p

For each gridNumber //循环遍历每一个网格的范围

compare(p, range);//比较p和每个网格的范围

sum+=1;//统计数据点个数

sumValue+=value;//统计一个网格内所有记录的数据和

average=sumValue/sum;//求质心

context.write(gridNumber,p);//给每条记录标记所属网格，便于删除不可能成为离群点的点集

for each gridNumber //第2次遍历

Max = distince(p,average);//计算每个点和质心的距离,即簇半径，每次只保留最大值

hashMap1.add(gridNumber,Max); //将计算后的数值存储到hashMap中

sort();//根据sum值升序排列

Iterator it = map.entrySet().iterator();

while(it.hasNext()){

for i from 0 to n-1//循环遍历hashMap,取出值最大的n个数

print hashMap.getKey();//将这些网格编号输出

4 LOF算法的应用

为了降低LOF的时间复杂度，设定Nk(p)为点p的k–近邻点，则定义点p的k–近邻分布密度为[4]：

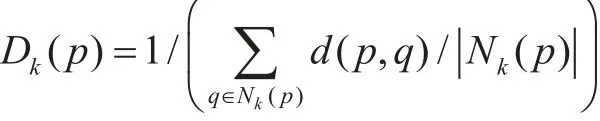
则p的局部离群点因子（LOF）为：

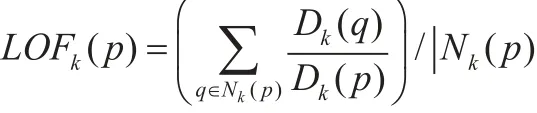
在用LOF算法进行离群点检测的时候，只需要簇半径最大的n个网格中的数据和它的邻居网格中的数据，其它编号的网格数据就可以删除了，此时，大数据集已经大大减少了。

5 验证

实验中总共使用10台机器来搭建云计算环境，其中一个是主节点（master），用来管理其它的节点，其它9台作为工作节点（slave），用来运行MapReduce任务。实验数据是国内某公司2013年动车组运行的所有闸片数据。

闸片数据说明如表1所示。

表1 闸片数据说明

实验1：为了证实网格聚类算法改进的有效性，选取2 GB动车组闸片数据，每条数据由6个属性组成，每维数据分别均分为2，5，10，12个等长的间隔，选取9个节点参与计算，实验结果如图1所示。

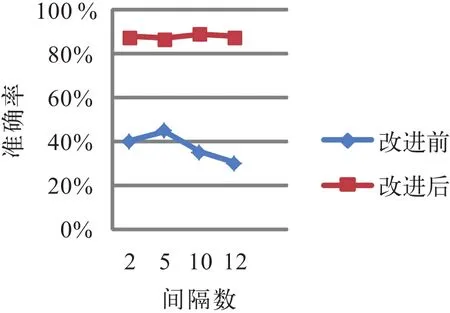
图1 改进前后结果对比

实验结果表明：算法改进前，网格聚类的准确率变化很大，说明网格划分对正确率影响较大，并且聚类结果不甚理想。算法改进后，不管网格如何划分，聚类正确率都保持在一个较高并且平稳的状态。说明算法改进是有效的。

实验2：比较在Hadoop分布式运行环境下，数据量和节点数不同时，程序运行时间。实验分别采用3组数据集，数据大小分别为5 GB，10 GB，15 GB，每条记录由22维数据值的数据组成，除速度和总里程外，其它数据都是以十六进制形式存储的。每维数据均分为5个等长的间隔，分别选择1, 3, 5, 7, 9个节点参与计算，实验考察在逐渐增加节点的情况下，网格聚类算法的执行效率。

网格聚类过程中对记录标识网格编号，生成结果如图2所示 。

图2 网格聚类实验结果

执行时间如图3所示。

从实验中可以看出每个作业的执行时间随着节点数的增加而降低。由此证明，增加节点数可以显著提高系统对同规模数据的处理能力。

图3 网格聚类时间

6 结束语

本文旨在利用基于离群点因子的离群点检测算法LOF来查找多维海量时序数据中的离群点，在MapReduce基础上利用网格聚类减小数据集，能够有效减小LOF算法的时间复杂度。实验证明了提高网格聚类检测精度所做的改进是有效的。

[1] 刘明华，张晋昕.时间序列的异常点诊断方法[J]. 中国卫生统计，2011，28（4）：478-481.

[2] 郭逸重. 一种基于孤立点挖掘的Hadoop数据清洗算法的研究[D]. 广州：华南理工大学, 2012.

[3] 杨正宽.基于距离的离群挖掘算法研究[D]. 重庆：重庆大学，2011.

[4] 郑斌祥，席裕庚，杜秀华．基于离群指数的时序数据离群挖掘[J]．自动化学报，2004，30（1）：70-77．

[5] 文 琪，彭 宏．小波变换的离群时序数据挖掘分析[J]．电子科技大学学报，2005，34（4）：556-558．

[6] 翁小清，沈钧毅．基于滑动窗口的多变量时间序列异常数据的挖掘[J]．计算机工程，2007，33（12）：102-104．

[7] 杜洪波，张 颖．基于LLM的时间序列异常子序列检测算法[J]．沈阳工业大学学报，2009，31（3）：328-332．

[8]江小平，李成华，向 文，等.k-means聚类算法的Map-Reduce 并行化实现[J].华中科技大学学报（自然科学版），2011，39 （增刊I）：120-124.

[9] 曹洪其, 余 岚, 孙志挥. 基于网格聚类技术的离群点挖掘算法[J]. 计算机工程，2006，32（11）：119-122.

[10] 张天佑. 基于网格划分的高维大数据集离群点检测算法研究[D].长沙：中南大学，2011.

责任编辑 陈 蓉

Outlier Mining Algorithm for time series data based on MapReduce

LIU Feng1, YAN Wanmei1, LI Hongren2
( 1.School of Computer and Information Technology, Beijing Jiaotong University, Beijing 100044, China; 2. Yuanping Brach, Shuo Huang Railway Development Company Limited, Xinzhou 034100, China )

Aiming at outlier mining in massive time series data, the paper combined grid clustering with MapReduce programming model to exclude grids that was impossible to contain outlier, and then used LOF Algorithm to detect outliers from the rest grids. In order to improve the detection accuracy of the grid clustering, this paper proposed an improved algorithm based on clustering radius. Experimental results showed the effectiveness of the improvement. Experiment also analyzed the execution time grid cluster cost under the circumstances with different number of nodes, which proved it was suitable for handling massive time series data combined MapReduce with grid clustering.

massive time series data; grid clustering; MapReduce; LOF; clustering radius

U266.2∶TP39

A

1005-8451（2015）04-0001-05

2014-09-23

刘 峰，教授；延婉梅，在读硕士研究生。