探究化归思想,提高教学效益
李珍
【摘 要】初中数学课本虽然没有明确提出化归思想,但化归思想存在并贯穿于整个初中数学教学中,现如何将化归思想作为重要的数学学习思想纳入学生的认识结构中呢?本文从四个阶段依次来说明化归思想在数学教学中的运用。
【关键词】数学;化归思想;阶段
贝尔特拉米曾说“如果我们让学生用有意义的方式学习数学,他们应该学会数学地思维。”随着新课程的改革,对广大农村中学大面积提高教学质量,提出了新的挑战。学生知识掌握的程度严重参差不齐,要提高数学成绩确实存在很多困难。初中阶段的学生基本上能够阅读教材,大概明白所要学习的内容,但理解的不一定确切、全面、透彻,也不一定能抓住要领,常感到学习上有困难,同时没有掌握一套自学方法和养成独立解题习惯。因而不能独立学习,只能在老师的指导下一课一课或一章一节地进行相对独立的学习。初中数学课本虽然没有明确提出化归思想,但化归思想存在并贯穿于整个初中数学教学中,现如何将化归思想作为重要的数学学习思想纳入学生的认识结构中呢?为此,结合教学实践,对化归思想的教学历程作如下探究。
首先是化归思想的渗透阶段
这一阶段主要从初一上学期开始,初一的教材中有很多地方就体现了化归思想。因此,我们在平时的备课中应理清其思想脉络,适时渗透归纳,如课本中诸如“当作”、“看成”等等的表述就是渗透化归思想的信号,同时,我们还应看到每一个定理、公式都是化归思想的一个范例。因此,教师要在课堂教学中把每一个定理的证明思路暴露给学生,讲清定理证明的思维过程,讲清定理的化归思想,每一个定理的证明,就是一道非常好的化归例题,所以,教师在定理的教学中不应只注重定理的应用,更应重视定理的证明。在教学中,如果有意识地加强对化归能力的训练,可有效地促进学生思维的发展,帮助学生克服思维障碍,使知识产生正迁移,从而提高学生的解题能力。初一学生刚跨入中学的大门,是兴趣和情感的高峰期,我们要抓住时机,有计划、有意识、逐步地把化归思想渗透到学生的认识结构中,以孕育化归的潜意识,以便提高教学质量和解题技巧。如:七年级一道练习题“一条直线上有3个点,则这条直线上有几条线段? 4个点呢? 5个点呢? n个点呢?”。通过学生讨论交流、教师引导得出结论1-2 n(n-1),我们可以转化引导学生解决同样问题:①我们年段5个班参加篮球比赛(每个班之间都要打一场),共有几场比赛?②平面上有公共端点的n条射线,能组成几个角(小于平角的角)?
其次是化归思想在教学中的意识阶段
这一阶段一方面在认识活动中,教师要有意识地提供数学知识发生的背景材料,展示知识的发生过程,因为数学史是由曲折反复的事件构成,数学发展的每个时期都充满了可歌可泣的故事,数学故事展示了数学思想与数学方法及人类其他活动的相互关联,其本身就是文化历史和人情世故产物,具有生动、幽默的特质。若在教学中融入相关数学史的知识,既有助于学生数学知识的学习,又能提升数学的文化功能,更能激起学生的好奇心,使学生更好地领会所学的知识,并能调动学生学习的积极性。另一方面,在教学解题活动中,教师要有意识地引导学生将问题转化,使之变为已经解决的问题或较易解决的问题,并展示化归脉络。如:化生疏为熟悉、化抽象为直观、化含糊为明朗、化减法为加法、化除法为乘法、化繁为简、化难为易、化未知为己知、化复杂的图形为简单图形、化多元为一元、化高次为低次、化二元一次方程组为一元一次方程、化分式方程为整式方程、化梯形为特殊四边形或三角形问题等等,都是解决问题的一种最基本的思想,从而将化归意识潜移默化地纳入学生的思维轨迹。
再次是化归思想在教学中的形成阶段
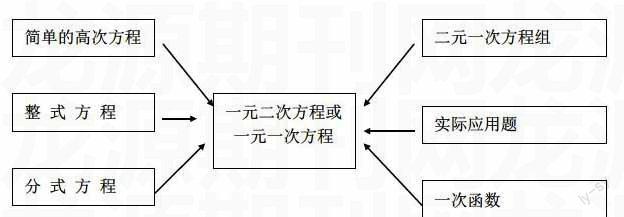
化归思想在学生解决问题过程中的形成阶段,主要从初三开始,如九年级一元二次方程教学中,我们可以让学生自己先根据教师有意识的化归启发,观察、比较、分析寻找答案,得出解方程規律,并在学完本章后,可引导学生运用化归思想将解各种方程的思路作出如下梳理:
通过梳理展示,不仅突出了本章的知识重点,而且明确了解各类方程的化归目标,更重要的使化归意识同步渗入学生的认识结构,这时可抓住时机介绍化归思想,揭示其内涵、外延及其功能和作用,并出一些练习题强化化归意识的形成。如:解方程:(3x+5)2-4(3x+5)+3=0此题我们要有意识有目的地引导学生转化解题思想,设3x+5=y,则原方程可化为y2-4y+3=0,然后利用已学知识解出y的值,再把y的值代入3x+5即可求出原方程的解,从而使问题简单化。
最后是化归思想在教学中的应用阶段
数学家路莎·彼得曾说“数学家们也往往不是对问题进行正面攻击,而是不断地将它变形,直到把它转化成能够得到解决的问题”。解题是数学的心脏,一旦学生形成了一定的化归意识,我们就可以让学生就用化归思想分析和解决问题。事实上,解题的过程就是从题目的重要条件不断向解题目标变形、靠近的过程,因此,利用目标导航,进行灵活转化是让解题思路来得自然的重要途径。首先在应用阶段我们主要有三种途径:①在自学或接受新知识时,让学生回忆联想,对知识追根求源,理清知识的来龙去脉;②在复习时,让学生对知识进行归纳梳理,形成系统;③在解题时让学生学会分析,执课索因,不断变换转化问题。第二我们在运用同时也要有目标,必须要遵循四个原则:①熟悉化原则,将陌生的问题转化为熟悉的问题,以利于运用熟悉的知识、经验和方法来解决;②简单化原则,将复杂的问题转化为简单问题,通过对简单问题的解决,达到解决复杂问题的目的,或获得某种解题的启示和依据;③和谐化原则,转化问题的条件和结论,使其表现形式更符合数与形内部所表示的和谐统一的形式;④直观化原则,将比较抽象的问题转化为比较直观的问题来解决。总之,这些途径和原则既可应用于沟通数学各分支学科的联系,又能调动各种方法与技术,从而使化归思想从意识应用过渡到有意识应用阶段,让化归思想真正成为他们今后学习数学、应用数学的思想武器,最终达到解题的简捷性。
总之,以上四个阶段并无严格的界限,而是彼此交错、循环往复、螺旋上升的。因此,化归思想的教学是一项系统工程,它的形成要经历漫长的过程,从模糊到清晰,从无意识到有意识。我们应从长计议,潜心研究,精心设计教学活动,使化归思想和数学基础知识产生共鸣,并伴随教学过程为学生掌握、应用和发展。