平行双导线电磁场特性可视化模拟实现
安爱民,张爱华,张浩琛,丁守成
(兰州理工大学电气工程与信息工程学院电子信息系,甘肃兰州730050)
0 引言
“电磁场与电磁波”是电子信息专业一门重要的专业基础课,平行双导线的电磁场特性及分布是该课程中较为重要的知识点,平行双导线涉及的电磁波的理论本身比较复杂和抽象,学习者不仅需有较好的数学基础,还需有较强的空间想象能力和逻辑思维能力来理解它[1]。通过对平行双导线电磁场特性的理解,有助于加深对“电磁场与电磁波”主要理论知识的认识与理解。在教学过程中,常对场分布特性进行定性和定量的分析[2],理解与掌握这种分析过程对于初学“电磁场与电磁波”的学生来说有较大的难度,需要通过仿真与模拟实验等相关辅助教学环节帮助学生加深理解与认识。因此,常使用电磁场仿真软件或Matlab软件对一些电磁现象进行仿真描述,然而这些方法的仿真效果不太直观[3,4];同时,由于条件与课时的限制,学生不能亲自动手完成。针对上述教学环节存在的不足,本文通过引入VC环境下的科学计算与模拟平台就可,实现对平行双导线电磁场分布特性的可视化仿真模拟[5,6]。教学实践表明,该方法有助于学生对相关电磁场理论知识点的深入理解与掌握。
1 平行双导线及其电磁场描述
平行双导线是能传输TEM波的双导体系统,在传输TEM波条件下,电场与磁场只有横向分布[7]。
平行双导线的外形结构如图1所示,该系统由两根几何尺寸相同的导线平行布放构成。单根导线直径为d,两根平行导线圆心之间距离为D。假设所处环境的介质其介电常数和磁导率分别为ε和μ。
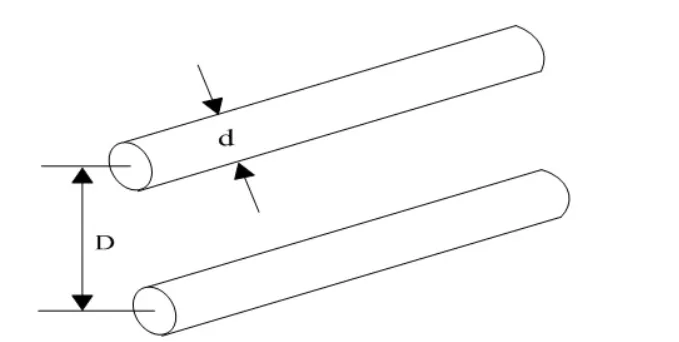
图1 平行双导线示意图
1.1 平行双导线的电场描述
现设平行双导线两导线单位长度带电量分别为+ρι和-ρι,同时满足 D≫d/2,可近似认为电荷均匀分布在两根导线的表面上。选取平行双导线中一根导线的横截面中心为坐标原点,建立如图2所示的坐标系。我们应用高斯定律和叠加原理,可以得到两导线之间的平面上任意一点P的电场强度为[5]

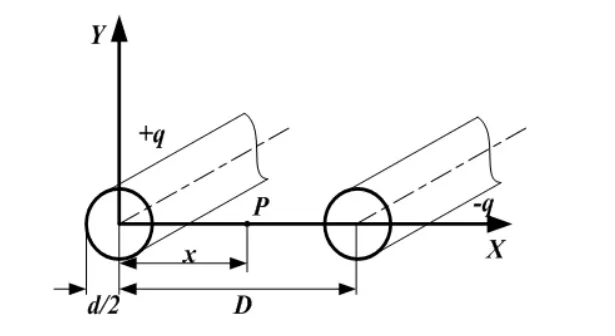
图2 平行双导线电场描述坐标系
1.2 平行双导线的磁场描述
设导线及其周围媒质的磁导率皆为μ,两导线中通过的电流为Ι,如图3所示,因为D≫d/2,故在计算导线外部的磁场时,可近似地认为电流集中于导线的几何轴线上。根据安培环路定理和叠加原理,可求得平行双导线之间的平面上任意一点P的磁感应强度为
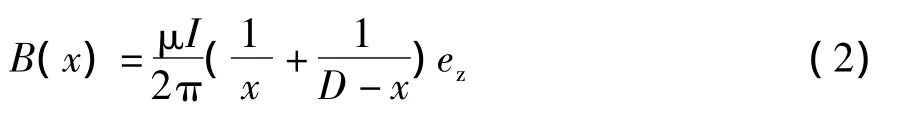
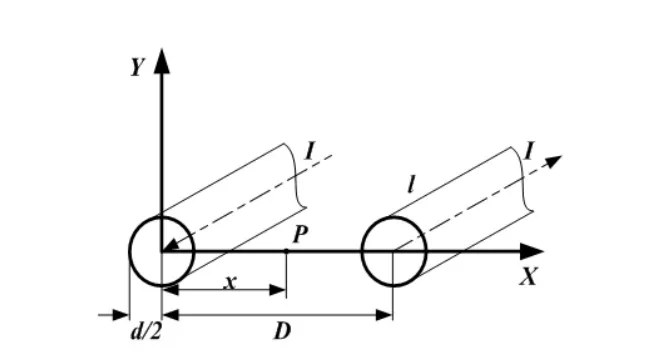
图3 平行双导线磁场描述坐标系
2 平行双导线电磁场特性可视化
平行双导线电磁场分布特性的可视化仿真实现步骤分为平行双导线模型建立、平行双导线电场强度分布可视化实现和平行双导线磁场强度分布可视化实现。本文使用的仿真环境是科学计算与模拟平台。该平台是在VC环境下开发出来的用于模拟以微分代数方程表述的一切动态变化物理现象的平台,具有容易掌握、使用灵活等优点[8]。
2.1 平行双导线的模型建立
在科学计算与模拟平台下,没有现成用于输入平行双导线模型的C输入函数。故在建立平行双导线模型时可以通过绘制两个圆柱体示意为平行双导线的两根导线。两个圆柱体的直径相同,轴向相同,长度相同,而高度不同,两者之间的高度用来表示平行双导线之间的距离。同时还应注意圆柱体的放置方向、圆柱体起点位置和中心点的选取及两个圆柱体之间的距离。在设计中将平行双导线两条导线的中心点和起点分别用以下语句定义为

2.2 平行双导线电场分布的模拟
在仿真实现中,用电场线来表示电场的分布特性。即用带箭头的矢量线来表示电场的方向,用电场线的疏密来表示电场的强弱程度。
当平行双导线两根导线是理想导体时,其电场方向是从带正电荷的导线指向带负电荷的导线,并且其电场分布为均匀的平行直线,如图4所示。
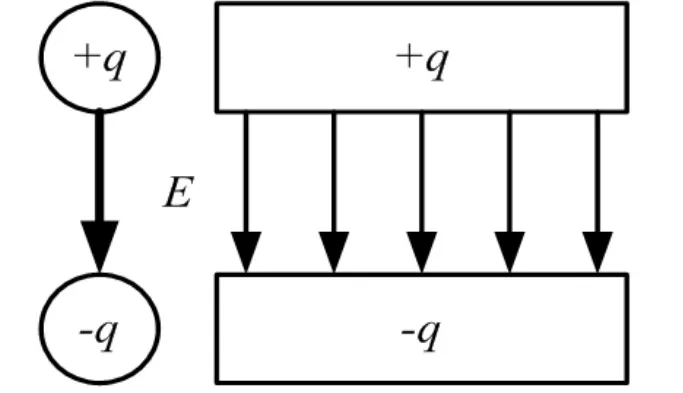
图4 平行双导线电场分布示意
平行双导线所产生的电场是随着位置的变化而变化,并遵循波动方程。在可视化仿真中,通过对平行双导线周围不同位置处的连续波动方程进行离散化,计算出每一个位置处产生电场值的大小,进而模拟出不同时刻平行双导线周围的电场变化规律。
在科学计算与模拟平台中,采用三个for循环产生的输出矩阵来表示每个点的位置,使用箭头表示电场在这一点的方向;将这些不同位置的点显示在科学计算与模拟平台中,将同一电力线的点用直线连接起来就可实现三维空间中平行双导线中电场分布的模拟。具体的程序流程如图5所示,模拟的效果如图6所示。
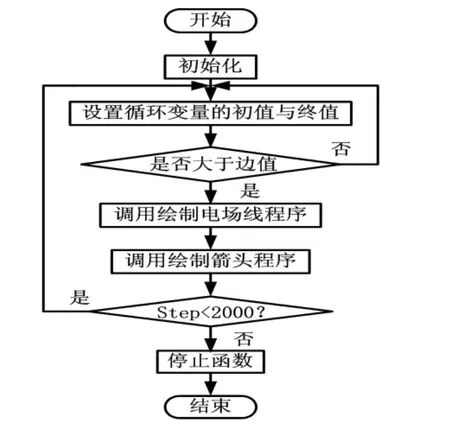
图5 平行双导线电场描述程序流程图
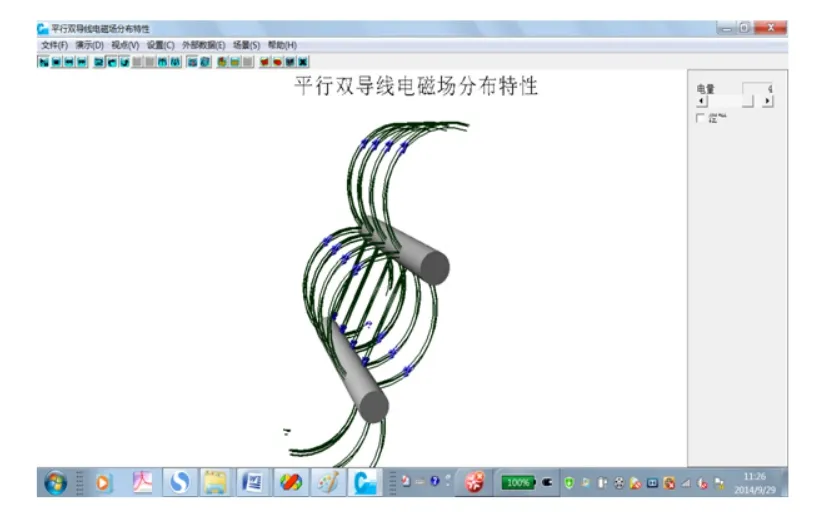
图6 平行双导线电场描述模拟示意图
在图6中,上面的导线带正电荷+q,下面的导线带等量负电荷-q,从图中可以看出,电力线是从上面带正电荷的导线发出,终止于带负电荷的导线,这与平行双导线电力线分布情况是一致的。
2.3 平行双导线磁场分布的模拟
平行双导线周围的磁场由每一根导线上传输的电流激发。本文中采用带箭头的圆线圈表示平行双导线的磁场分布,箭头的方向表示磁场的矢量方向,由右手法则确定。平行双导线两条导线的电流方向如图7所示。根据安培定律,可以得到如图7所示平行双导线磁场分布。对于平行双导线而言,可以通过离散磁场波动方程求出平行双导线周围不同位置的磁场分布。这些点处的磁场大小依据波动方程来确定,进而就可以描绘出平行双导线周围磁场分布的可视化动态图。
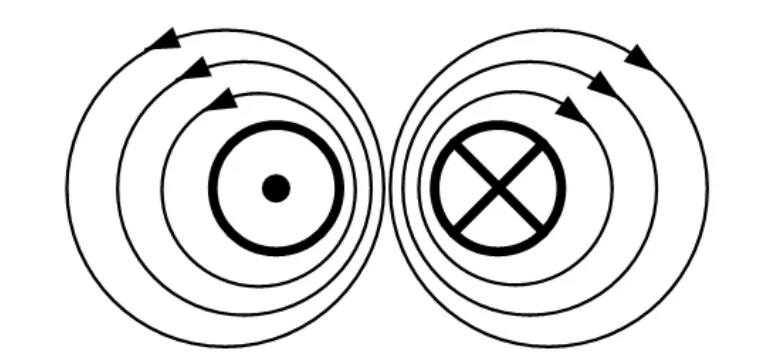
图7 平行双导线磁场描述示意
在科学计算与模拟平台中,输出的矩阵值只能代表该点在三维空间里的坐标,并非这一点的磁场值。根据这一特点,在程序设计的过程中采用三个for循环,输出的矩阵表示每个点对应的位置,而箭头的方向表示磁场在这一点的矢量方向;将其不同位置处的磁场值显示在科学计算与模拟平台中,将同一磁力线上的点连接起来,以体现平行双导线中磁场分布。每个循环表示该时刻不同位置处磁场的方向和大小,执行程序就可以画出连续的磁力线,箭头表示任意时刻磁场的矢量方向。具体的程序流程如图8所示,可视化模拟效果如图9所示。
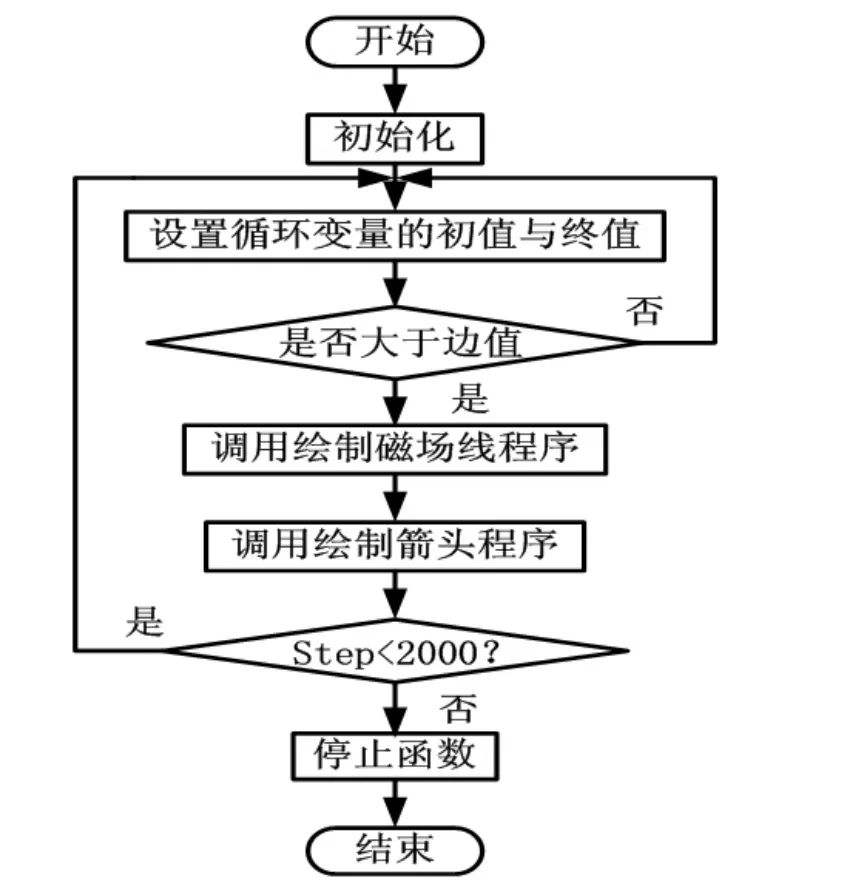
图8 平行双导线磁场描述程序流程图
2.4 平行双导线电磁场分布的模拟
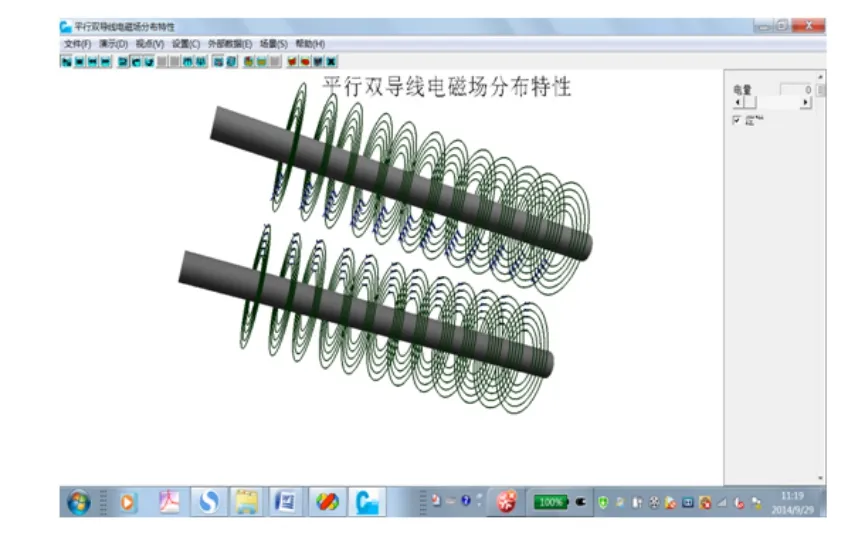
图9 平行双导线磁场描述模拟示意图
将上面平行双导线电场与磁场分布进行叠加,就可以得到平行双导线的电磁场分布。在程序实现上,就是把电场程序与磁场程序进行组合。具体仿真效果如图10所示。图10(a)和图10(b)分别表示了平行双导线在不同时刻带电量不同时其电磁场的分布情况。

图10 平行双导线电磁场分布
3 结语
针对“电磁场与电磁波”的教学环节中平行双导线电磁场分布特性学生较难理解和掌握这一问题引入了科学计算与模拟平台对其分布特性进行仿真模拟。利用科学计算与模拟平台强大的运算能力和图形可视化环境,将平行双导线电磁场分布特性直观地向学生进行展示。教学表明,这种方法不但可以加深学生对电磁场相关理论的理解,激发了学生的学习兴趣,同时也提高了学生对VC语言的使用能力,取得了很好的教学效果。
[1]马愈昭,许明妍,范懿.电磁场与微波技术课程的三种特色教学手段[J].武汉:武汉大学学报(理学版),2012,58(2):109-112.
[2]姜宁.在“电磁场与电磁波”教学中建立创新理念[J].南京:电气电子教学学报.2009,31(1):95-97.
[3]张祥军.“电磁仿真软件在电磁场与电磁波”课程教学中的应用[J].北京:中国电力教育,2010,2:150-152.
[4]吕秀丽,牟海维,李贤丽.Matlab在电磁场与电磁波实验教学中之应用[J].上海:实验室研究与探索,2010,29(2):110-112.
[5]安爱民,张爱华,黄玲.可视化数字模拟创新教学在“电磁场与电磁波”中的探索与实践[J].北京:电工技术学报.2014,28(8):204-208.
[6]安爱民,张爱华,张浩琛.同轴电缆的电磁特性可视化模拟与仿真实现[J].北京:电工技术学报.2014,28(8):167-171.
[7]苏东林.电磁场与电磁波(第二版)[M].北京:高等教育出版社,2009.
[8]李元杰,陆果.大学物理学(第二版)[M].北京:高等教育出版社,2008.

