时域分析法的教学难点及应对方法
骆 建,谢 榕
(华中科技大学电气与电子工程学院,湖北武汉430074)
0 引言
“电路理论”是一门非常成熟的课程。但在教学上仍有改进的必要。特别是对一些教学难点,即使学生课上能理解接受,课下仍难以应用自如。由于教学大纲要求和课时等原因,在教学时往往对于有些重点内容的深入探讨一带而过,对于大纲不作要求的一些教学难点更是无暇顾及。然而有些教学难点正是重要的教学内容,解决不好会直接影响学生对课程的掌握。因此,熟悉和掌握相关的应对方法,对教学是有益的。本文针对该课程中时域分析法这一教学难点,提出一些好学、好用的应对方法,与同行交流。
1 阶数判别
1.1 判别原则
时域分析法适合于一、二阶电路,对于一阶更为有效。如何辨别电路是一、二阶还是高阶,是决定是否采用时域分析法的第一步。一阶电路直观的辨别原则就是仅包含一个(等效)电容或一个(等效)电感的电路。否则,就是二阶以上的电路。
实际上电路的阶数决定于电路的齐次微分方程的阶数,所谓齐次就是与外施激励为零。因此,只要将外施激励置零,即电压源视为短路,电流源视为开路,简化电路的结构关系,电路的阶数就一目了然了。例如:在图1(a)中,当电源置零后即可知电路为一阶RC电路,而且二个电容结构关系是并联,时间常数也随之可定;在图1(b)中当电源置零后,就可以判断电路大于二阶,则该电路不适合用时域分析法来分析。
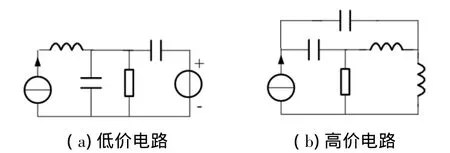
图1 有关阶数举例用图
1.2 应对方法
电源置零简化电路结构可以直观方便地判别属于时域分析法范畴的电路阶数(一阶或二阶),无需繁琐的列方程等数学推导。如是一阶电路,用此法同时也可以确定时间常数。使用时要注意独立电源的类型和换路开关的动作方向。当然上述方法也适合二阶电路的特征根的求解。
2 初始值的确定
初始值就是所求响应在换路后的瞬时值(设换路时间t=0),即t=0+时刻的值。它可由电容电压和电感电流的初始值及0时的等效电路求得。而电容电压和电感电流的初始值与其换路前一瞬间(t=0-)的值,即原始值有关,如换路时电容上电压和电感电流不跳变,则电容电压和电感电流的初始值等于其原始值,它们具有连续性;否则就须用电荷守恒或磁链守恒原理来求出[1-3]。
2.1 连续性的问题
初始值求解首先碰到的问题就是动态元件连续性的辨别问题。
在一般情况下,如电容有电阻串联(或广义串联),或电感有电阻并联(或广义并联),换路后一瞬间不会出现跳变问题。这是因为电阻起了缓冲作用(即电阻分压或电阻分流),使电容电压连续或电感电流连续。在外施激励有限的情况下,由于和电容串联的电阻上电压和电流有限,流过该电容的电流就不是冲激函数,即有电阻串联的电容上的电压就不会跳变;同理,有电阻并联的电感的电流也不会跳变。
例如,在图2(a)中,C1有电阻串联,其电压连续。C2和C3无电阻串联,如果C2和C3的电压原始值相加之和不等于电压源US,换路时强行使C2和C3的电压初始值之和等于US,则C2和C3电压不连续。假如并于电压源US的C2、C3路径上有一个电阻串联,或形成一个广义的串联,C2和C3电压就连续了。C4电压为US,不受换路影响。在图2(b)中,L1有电阻并联,其电流连续。L2和L3无电阻并联,如果L2和L3的电流原始值之和不等于IS,换路时强行使L2和L3的电流初始值相加之和等于电流源IS,则流经L2和L3的电流不连续。假如L2和L3支路节点上有一电阻支路并联,或形成广义的并联,其电流就连续。L4电流为IS,不受换路影响。
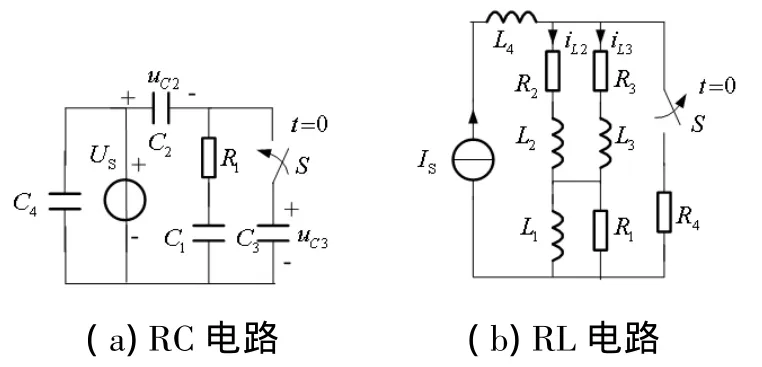
图2 有关连续性举例用图
2.2 应对方法
动态元件是否连续性的判别方法就是动态元件是否有电阻“作伴”,即:电容有电阻串联(或广义串联),或电感有电阻并联(或广义并联),则具有连续性。它直观方便地判别电容电压或电感电流是否有跳变问题。如果电容电压、电感电流连续,其初始值求解不难,为教学重点。如果不连续,则需用节点(割集)电荷守恒或回路磁链守恒原理来求,属教学难点。
3 三要素法
3.1 三要素法通式的理解
三要素法由线性时不变一阶微分方程的通解和特解演变而来,对于典型的外施激励(直流、正弦、非正弦周期),无需列写微分方程,直接可以通过三要素法的通式模型就可以求出符合初始条件的全解y(t),这可视为“无条件”[1-3]。
三要素法的通式模型为
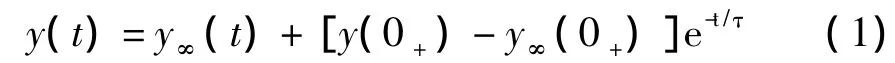
式中的 y∞(t)为 y(t)的稳态解,y∞(0+)为 y∞(t)在t=0+时的值,y(0+)为y(t)的初始值,τ为时间常数。
当外施激励为直流时,y∞(t)=y∞不随时间变化,式(1)通式模型则为
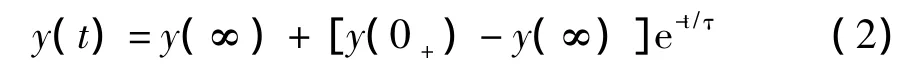
我们需要注意的是零状态响应通式模型y(t)=y(∞)(1-e-t/τ),而且,零输入响应通式模型y(t)=y(0+)e-t/τ是有条件使用的。首先尽管零状态响应来自于三要素法的通式模型,但零状态响应通式模型只能求解直流作用下的电容电压或电感电流,电路其他电压电流量的零状态响应则要酌情求解。其次,如所求响应稳态值不为零,则不能使用零输入响应通式模型。例如,在图3(a)中若电容电压初始值不都为零或不相等,或在图3(b)中若电感电流初始值不都为零或不相等,二个电路都是零输入响应,但各电容电压或电感电流不能单纯的套用零输入通式模型,但若用三要素法的通式模型就不受这些条件限制。所以一阶电路不管什么响应,可直接用三要素法的通式模型求响应。
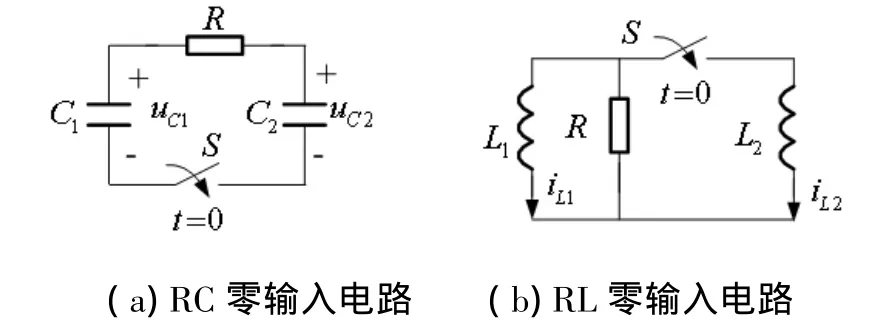
图3 有关通式举例用图
3.2 时域的表示
任何求得的响应表达式,都应赋予时域条件。
对于换路发生在t=0时的响应,有
我们要注意t≥0或t>0的区别,如果y(0+)=y(0-),则用t≥0,一般用于不跳变的电容电压或电感电流等的响应;如果y(0+)≠y(0-),就用t>0。
时域表达式还可以用单位阶跃函数ε(t)来表示,对于阶跃响应、冲激响应都有ε(t)伴随。对于式(4)其等价表示为
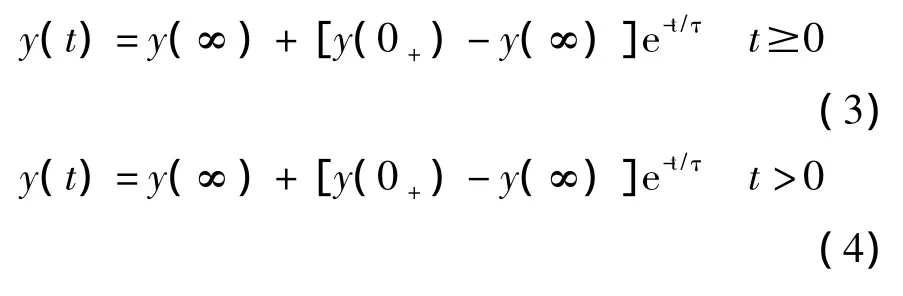
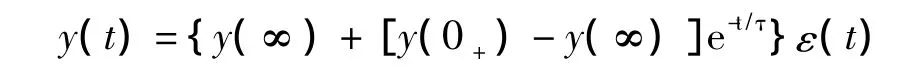
这种时域表示方式不仅只用一个数学表达式就能反映出各时段的状态,还可以在其运算中捕捉到换路时刻的瞬间状态。例如电感电流的全时间域响应为
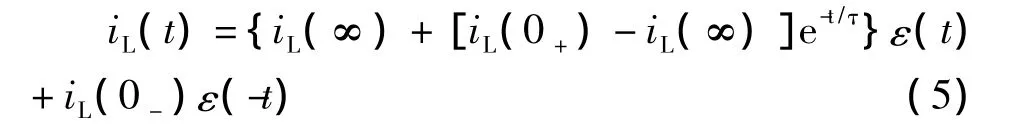
则电感电压为
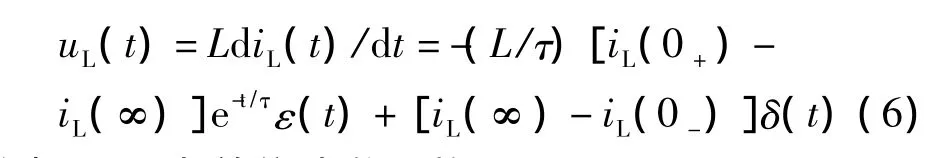
式中,δ(t)为单位冲激函数。
由此例可以看出这种方法不仅能得出t>0响应描述,还可以捕捉到t=0瞬间状态,如iL(0+)=iL(0-),就没有冲激分量。它与时域分段分析吻合,分析既严谨又方便。不过要注意的是解答一定要是全时域上的表达式,如式(5)中的iL(0-)ε(-t)项不能漏掉,否则结果就不正确[4]。
3.3 应对方法
对于一阶电路的分析,要注意理解三要素法通式模型的“有条件”和“无条件”,包括伴随的状态和时域等细节。细节决定成败,归根到底还是概念的问题,不注意细节,三要素法这个重点的掌握就只在表面上。
4 阶跃响应和冲激响应求解的局限
4.1 阶跃响应和冲激响应的问题
阶跃响应是在单一阶跃函数激励下的零状态响应,实际就是在单一直流作用下的零状态响应。单位阶跃响应设为S(t)。
冲激响应是在单一冲激函数激励下的零状态响应,实际上是由冲激函数改变零状态的零输入响应。单位冲激响应设为h(t)。
求解阶跃响应和冲激响应常用的方法有二种[5]:①直接法,其中求冲激响应的直接法多采用二步法,即先求电压或电流跳变量,再转化求零输入响应;②通过两者之间的关系来求,它们之间的关系可表达为
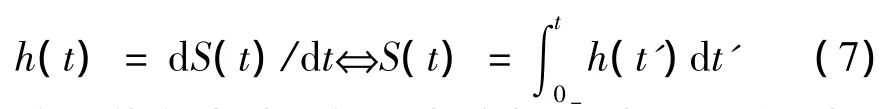
这二种方法对大部分电路都可以通用,但对于有些电路是有局限性的。例如:在图4(a)和图4(b)电路中,若用阶跃响应来求冲激响应就难行得通。又如,在图4(c)电路中,直接求冲激响应也比较困难。
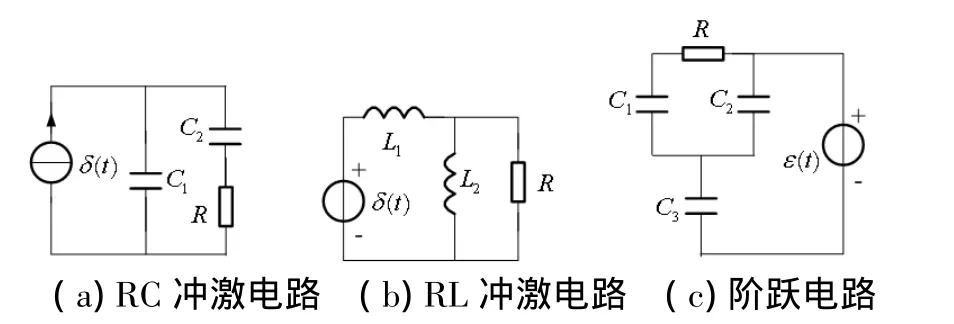
图4 有关求响应局限举例用图
按前面的电路阶数判定方法,图4(a)和图4(b)电路是一阶电路;求阶跃响应稳态解时,由于在直流电路中电容开路,电感短路,图4(a)电路中电流源出现开路,图4(b)电路中电压源出现短路情况,因此电路理论上是不能工作的,所以其冲激响应不能借助于阶跃响应来求。
这二个电路直接求冲激响应用二步法不难,也无需列写微分方程,例如在求图4(a)电路的冲激响应时(设各电容电压方向上正下负),第一步求冲激电源所建立的电路的初始条件,在t=0(0+~0-)等效电路中电容零状态可视为短路,C1的电流为冲激电流δ(t),则其电压跳变量为uC1(0+)=1/C1,C2无冲激电流,其电压uC2(0+)=uC2(0-)=0;第二步求初始状态引起的零输入响应,t>0后冲激电源为零视为开路,其分析与图3(a)电路相同。
图4(c)电路也是一阶电路,若用二步法直接求冲激响应,第一步求冲激电源所建立的电路的初始条件。因电容零状态视为短路,电压源就面临短路问题,此时电路实际是不能工作的,所以其阶跃响应不能借助于冲激响应来求。这个电路用三要素法求阶跃响应时,涉及到电荷守恒原理求跳变值和稳态值,其三个要素求解为(设各电容电压上正下负)。
(1)求初始值:在换路时刻,C1有电阻串联,这时其电压不会跳变,C2和C3会发生跳变,于是根据-C2uC2(0+)+C3uC3(0+)=0及uC2(0+)+uC3(0+)=1两个式子求解便可得C2和C3的电压初始值;
(2)求稳态值:稳态时电容视为开路,则根据-C1uC1(∞)-C2uC2(∞)+C3uC3(∞)=0和 uC2(∞)+uC3(∞)=1及uC1(∞)=uC2(∞)三个式子求解便可得C1、C2和C3的电压稳态值;
(3)求时间常数:根据前述的电源置零方法,电压源视为短路后,电容的等效关系显而易见为C1串联于C2和C3并联,则时间常数τ=RC即可求之。
4.2 应对方法
处理阶跃响应或冲激响应就是依据电压源是否短路、电流源是否开路来选择可行的方法。当然阶跃响应或冲激响应电路的数学描述可以借助于对应的求导或积分得出。
5 结语
本文所讨论的内容为教学中常见的知识点,并非偏僻内容。合理用好这些知识点,有助于巧妙地解决教学难点。探索对应的教学方法对提高教学质量无疑是很有意义的。
[1]汪建.电路原理[M].北京:清华大学出版社,2008
[2]颜秋容,谭丹.电路理论[M].北京:电子工业出版社,2009
[3]邱关源,罗先觉.电路(第五版)[M].北京:高等教育出版社,2006
[4]田社平,陈洪亮.动态电路全时域响应的求解[J].南京:电气电子教学学报,2009(1):19-21
[5]汪建.用时域分析法求解冲激响应的方法[J].南京:电气电子教学学报,2011(6):103-105

