“信号与系统”中的STFT概念引入

闫允一，郭宝龙，朱娟娟，孟繁杰

(西安电子科技大学空间科学与技术学院智能探测系，陕西西安710071)

0 引言

“信号与系统”是电子信息类专业的主干基础理论课程，是后续众多专业课程的前导[1，2]。我们在本课程体系内引入与其他后续专业课程的相关概念，可以给学生和读者打开一扇通向专业领域的窗户。其中的专业内容和涉及理论，可以依据各校自身的办学特色进行变更或调整。

现行的“信号与系统”内容体系中大多以傅里叶变换、拉氏变换和Z变换为核心展开，内容涉及连续以及离散系统的分析。但三大变换均不具备对信号进行时域局部分析的能力，而具体的应用场景中则往往需要对信号进行时域局部分析，因此有必要在“信号与系统”课程中增加时域局部分析工具的介绍。其中，短时傅里叶变换STFT(Short Time Fourier Transform)是比较经典的具备时域局部分析的工具。它和傅里叶变换又是小波分析中绕不过去的铺垫，其发展历史也决定了其必然性。短时傅里叶变换中的时频联合分析概念在小波变换WT(Wavelet Transform)得到了进一步的发展和改进[3]。因此，通过对傅里叶以及短时傅里叶变换及其局限的分析，能够比较顺畅地引入小波变换。

傅立叶变换得到的傅立叶系数是不随时间变化的常数[4]。事实上，求傅立叶系数是全时间域上的平均(因为系数计算是整个时域上进行积分)，局部突变的作用很难反映出来。为此，人们首先想到的解决方案就是对傅里叶变换的时域作用区间进行限制，也称加窗傅里叶变换的STFT应运而生。

1 平稳信号与非平稳信号

实际上一种数学变换是否适合于某个领域，除了与变换本身的特性有关之外，还跟待分析的信号的特性有非常大的关系，而信号是否平稳是一个非常关键的要素。对于确定信号，如果信号的频率成分随着时间而发生变化，那么这样的信号称为非平稳信号;若信号的频率成分与时间无关，则称为平稳信号。

很多实际信号都是非平稳信号。比如脑电图波形因激动、放松、浅睡、熟睡和深睡等不同状态而大为不同，即便是在每个状态之内信号的非平稳性也非常明显。傅里叶变换给出了信号中包含的频率信息，但是并没有告诉我们某个频率信号是在何时出现的，分析非平稳信号具有明显局限。[例1]试对如下信号做傅里叶幅频特性分析

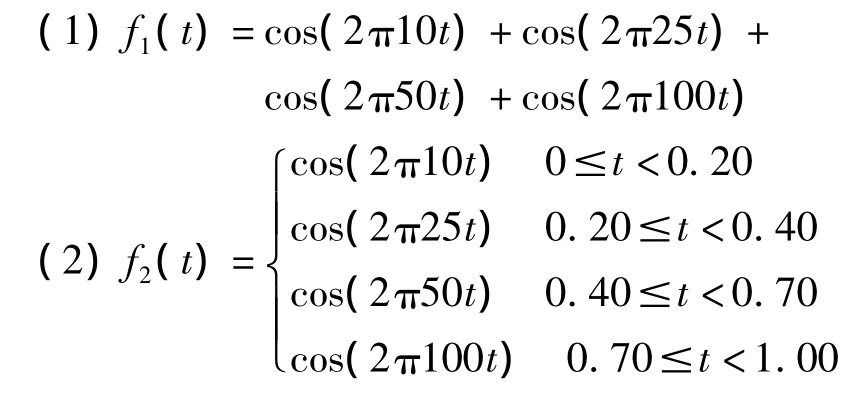
解:f1(t)是一个平稳信号，频率为10Hz，25Hz、50Hz和100Hz的分量出现在整个时域内，其时域波形如图1(a)所示。从图1(b)的幅频特性图中，可以明显地看到四个频谱分量分别对应着相应的频率。

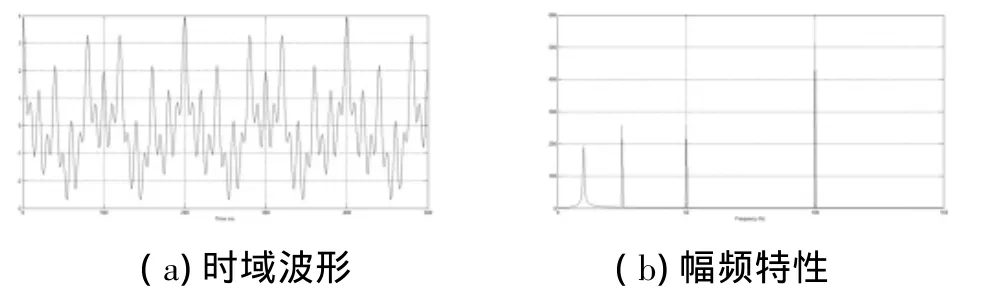
图1 f1(t)时域波形和幅频特性

f2(t)包含四个频率分量的信号，它们分别在不同时刻出现，因此这是一个非平稳信号，其时域波形如图2(a)所示。由图2(b)的幅频特性可以看到依然有四个尖峰，且50Hz和100Hz分量的幅度比25Hz和 10Hz分量大，这是因为高频信号时长(300ms)比低频信号时长(150ms)大。若忽略掉因频率突变引起的毛刺(有时候他们与噪声很难区分)和两幅图中各频率分量的幅值(这些幅值可以做归一化处理)，图1和图2的频谱图几乎是一致的，虽然相应的时域信号之间差别很大。这说明:平稳信号与非平稳信号在时域内可能具有完全不同的波形，但在频域内却可能具有非常相似的傅里叶频谱特性。

图2 f2(t)的时域波形和幅频特性

2 傅里叶变换的局限

傅里叶变换无法有效地处理这样的非平稳信号。傅里叶变换的实现过程可以写成如下的形式:

傅里叶变换隐藏了原信号的时间位置信息，不能区分频率成分出现时间不同的信号，不具备时域的分辨率。因此傅里叶分析不适合于分析频率随时间而变化的非平稳信号。分析非平稳信号时，我们往往要兼顾时间和频率两方面的信息。短时傅里叶变换STFT是一个比较常用的解决方案。

3 短时傅里叶变换STFT

很多实际的系统分析中，需要同时知道局部范围内的频率信息和时间信息，而不是全局或者整体的平均数值，此时傅里叶变换就不合适了。实际系统中的非平稳信号往往在一定的时间区间内的是保持平稳的，通过时域内的窗函数提取出非平稳信号的平稳部分，然后进行傅里叶变换就可以知道其频率信息，而窗函数的位置就提供了时间信息。

[定义]对时域内平方可积信号x(t)∊L2(R)和窗函数 W(t)，定义

为x(t)的短时傅里叶变换，其中，x(t)是信号本身，W(t－τ)是中心位于τ位置的时域窗函数。需要注意的是，一般而言，τ落后于t，且其分辨率要低于t。τ往往是离散的几个点，而不是像t一样是连续的。当窗函数为高斯函数时，该变换被称为Gabor变换。

STFT只不过是对乘了一个窗函数的信号做傅里叶变换。STFT将信号在时间域内分为若干足够小的片段，每个片段都可以看成是平稳信号。STFT需要窗函数的宽度应与信号片段的宽度相匹配，以确保窗内信号平稳性有效。因此，短时傅里叶变换又被称为加窗傅里叶变换WFT(Windowed Fourier Transform)。[例2]已知0.25，0.25i)，并且窗函数 W(t)=e-1000t2/2，试对该信号用短时傅里叶变换进行分析。

解:f3(t)实际上是一个分段平稳的非平稳信号，其时域波形如图3(a)所示。信号共有四个频率分量分别为 400Hz，200Hz，100Hz和 50Hz，振幅分别为1，2，3和4，按照时间顺序它的各分量分别作用0.25秒。该信号的STFT结果如图3(b)所示。

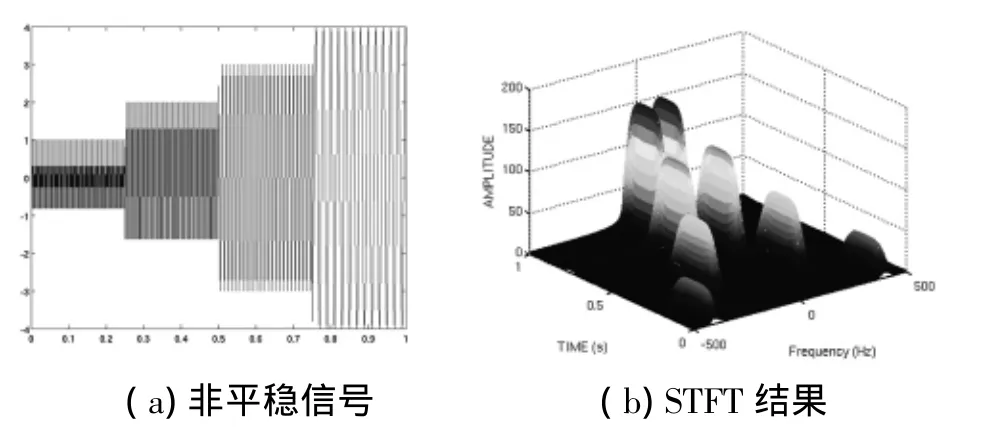
图3 一个非平稳信号及其STFT结果

从STFT结果可以看到，STFT以频率中线为轴对称的。因为STFT只不过是加过窗的函数的傅里叶变换。四个波峰对应着四个分量，在时间轴上对应着不同的位置，这意味着原始信号的四个频率分量也都出现在不同的时间段内。因此，我们得到的是原始信号的一个时—频联合表示，即不仅表明了信号中都有什么频率分量，还给出了各分量的作用时间。

4 短时傅里叶变换的局限

STFT给出了信号的时频表示，看起来已经解决了时间和频率共存的问题。但测不准原理表明，在实际的物理系统中不能获取信号绝对精确的时频表示。在短时傅里叶变换中，时间窗口宽度不变，在较长的时间窗内，高频信号的变换系数可能是很多周期的平均值，无法对局部特征进行刻画;若减小时间窗，高频信号能够被捕捉到，但无法刻画低频信号，因为在一个很短的窗口内观察到的低频信号变化可能小到无法检测。

综合考虑傅里叶变换和短时傅里叶变换，我们会发现存在这样一个矛盾:如果给定一个无限长的窗函数，会得到完美的频率分辨率，但是变换结果中完全不包含时间信息;要使用傅里叶变换进行分析，其前提是信号应该是平稳的，那么为了获得平稳性，我们必须要用一个宽度足够短的窗函数，时间分辨率较高，信号平稳性也越好，但频率分辨率却越低。

在使用STFT之前首先面临的问题就是窗函数的选择问题。如果原始信号中的频率分量能被分离出来，或者能通过其他手段来估算频段构成，那么可以牺牲一定的频率分辨率，用一个较窄的窗来追求更高的时间分辨率;否则，若无法获得原始信号的频率信息，那么完全没有办法保证窗函数能够适于进行信号的时频分析。

短时傅里叶变换试图通过窗函数来兼顾时间和频率分辨率，但在整个变换过程中保持恒定，本质上是一种分辨率单一且固定的分析方法。要想对依据非平稳信号的频率特性进行自适应分析，需要分析工具具备多分辨分析能力。小波变换中时移—尺度联合分析在一定程度上解决了信号分析中能兼顾时域分辨率和频域分辨率的问题。

5 结语

传统的“信号与系统”课程体系以傅里叶变换为代表的三大变换为核心展开。但傅里叶变换不具备局部时域分析的能力，这在实际工程应用有一定的局限性。短时傅里叶变换STFT通过引入时间窗，可以实现对特定时域范围内信号的分析，一般无法依据信号自适应地进行调整窗口宽度，是一种单一分辨率的分析方法。STFT所蕴含的时频联合分析概念，在实际应用中具有极大价值，并且对进一步引入多分辨分析概念具有前导和铺垫作用。

[1]郑君里谷源涛，信号与系统课程历史变革与进展[J]，南京:电气电子教学学报，2012(02).

[2]郑君里，试谈电工程与信息科学领域基础课程教学改革[J]，南京:电气电子教学学报，2006(01).

[3]邓东皋，彭立中，小波分析[J]，北京:数学进展，1992(03)

[4]李亚峻，史兴荣，李毅 傅里叶变换在信号处理中的优越性[J]，长春:数学学习与研究，2012(07)