等同双原子Jaynes-Cumm ings模型的量子特性及系统光谱
张丹凤,吕树臣
(哈尔滨师范大学光电带隙材料省部共建教育部重点实验室,黑龙江哈尔滨 150025)
等同双原子Jaynes-Cumm ings模型的量子特性及系统光谱
张丹凤,吕树臣*
(哈尔滨师范大学光电带隙材料省部共建教育部重点实验室,黑龙江哈尔滨 150025)
在全量子理论的背景下提出两个二能级原子分别与一单模腔场相互作用的系统模型,利用量子主方程和数值模拟计算等方法,研究该体系中腔场平均光子数、Mandel's Q因子及二阶量子相关度在非稳态时的变化规律。此外,对体系中原子及腔场中光谱结构进行了分析。结果表明:减小腔场耗散系数,增大原子间耦合系数,体系量子特性愈加明显。体系光谱呈现出Mollow三重峰结构,且原子辐射谱强度远大于腔场辐射谱强度。当原子跃迁频率与腔场跃迁频率为近共振时,Mollow峰值为三峰中最大值。此外,增大原子与腔场间耦合系数,可增大原子光谱的中峰强度;而增大腔场光谱的中峰强度,则需减小原子与腔场间耦合系数。
量子主方程;双耦合二能级系统;亚泊松分布;反群聚效应;自发辐射光谱
1 引 言
Jaynes-Cummings[1](简称J-C)模型是描述单个理想二能级原子与单模辐射场相互作用的可精确求解的模型。人们基于这一模型做了大量的研究,利用全量子理论及近代科学实验手段,发现了该系统中许多有趣的量子特性,如原子的压缩效应[2]、真空拉比分裂[3-4]、辐射光谱的坍缩和复起[5-6]、原子辐射的反群聚现象和光子数的亚泊松分布[7-8]等,并被实验所证实[9-10]。然而,在J-C量子体系中,多体耦合效应可能会对该系统产生巨大的影响。近年来,基于两个全同的二能级原子与量子化光场相互作用的Tavis-Cummings[11](简称T-C)模型受到了研究者的广泛关注,人们开始研究双原子与单模光场相互作用系统中的双光子过程[12-13]、双原子与双模光场的压缩态[14]以及多能级原子对T-C模型的影响[15]。研究结果表明:原子与辐射光场间均存在明显区别于经典辐射场的量子纠缠演化特性,而较好的量子纠缠态有助于量子计算及量子通讯[16-17],对于实现具有高保真度的量子信息技术的发展有着巨大的推进作用。Li等[18]研究了双原子与两个相互分离单模腔场的纠缠特性,但并未考虑两原子间的相互作用对体系的影响。
本文研究了具有相同耦合系数的双耦合二能级原子与两个单模腔场相互作用体系的量子起伏特性,考虑在两原子间相互耦合条件下,其腔场耗散系数、腔场耦合系数对系统平均光子数、Mandel's Q因子及二阶量子相关度的影响。除此之外,为了推理腔场内光场与物质相互作用的过程,加深对体系量子特性的理解,本文通过单光子近似过程,利用数值计算模拟等方法,对腔内原子的辐射谱及腔内光场的辐射谱进行了深入的研究。结果表明:原子辐射谱强度强于腔场辐射谱强度;当原子跃迁频率与腔场跃迁频率相比拟时,增大原子与腔场耦合系数可增大原子辐射光谱强度。
2 双原子-双腔耦合系统模型及基本原理
双原子-双腔耦合系统理论模型如图1所示,包括两个彼此分离但相互耦合的单模腔场C1、C2,两个全同的二能原子1和2,且分别位于两腔场中。
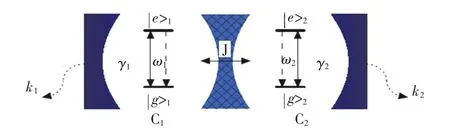
图1 双原子-双腔耦合系统模型Fig.1 Double atoms-double cavities coupling system model
考虑两原子在初始时刻均处于激发态,在旋波近似(RWA)下,该体系的Hamiltonian(=1)表示为:
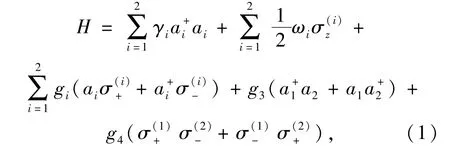
其中ωi(i=1,2)表示第i个原子的跃迁频率, γi(i=1,2)为第i个腔场的跃迁频率,、ai(i=1,2)分别表示第i个腔场中光子的产生和湮灭算符分别为第i个原子的反转、状态变迁(升与降)算符,gi(i=1,2)表示原子与腔场的耦合系数(其中g1表示第一个原子与第一个腔场的耦合系数,g2表示第二个原子与第二个腔场的耦合系数),g3表示两腔场间的耦合系数,g4表示两原子间的耦合系数。在玻恩-马尔可夫近似下,包括原子与腔场损耗的Lindblad形式的量子动力学主方程可表示为:

其中k1、k2分别为两腔场的耗散系数。
为计算腔场内的平均光子数〈a+1a1〉(本文以第一个腔场为例),可利用对算符求期望值的定义及其结果对时间求导关系式:

而算符a、a+、σ+、σ-、σz满足如下对易关系:

联立方程(1)~(4),并利用在求迹符号下算符乘积次序的可轮换性质,可得出双原子-双腔耦合系统算符期望值的运动方程。利用数值模拟仿真等方法,即可研究该体系的量子效应。
为计算原子和腔场的辐射光谱,可在单光子近似〈σza〉=-〈a〉下,由方程(1)~(4)推导得出如下微分方程组:
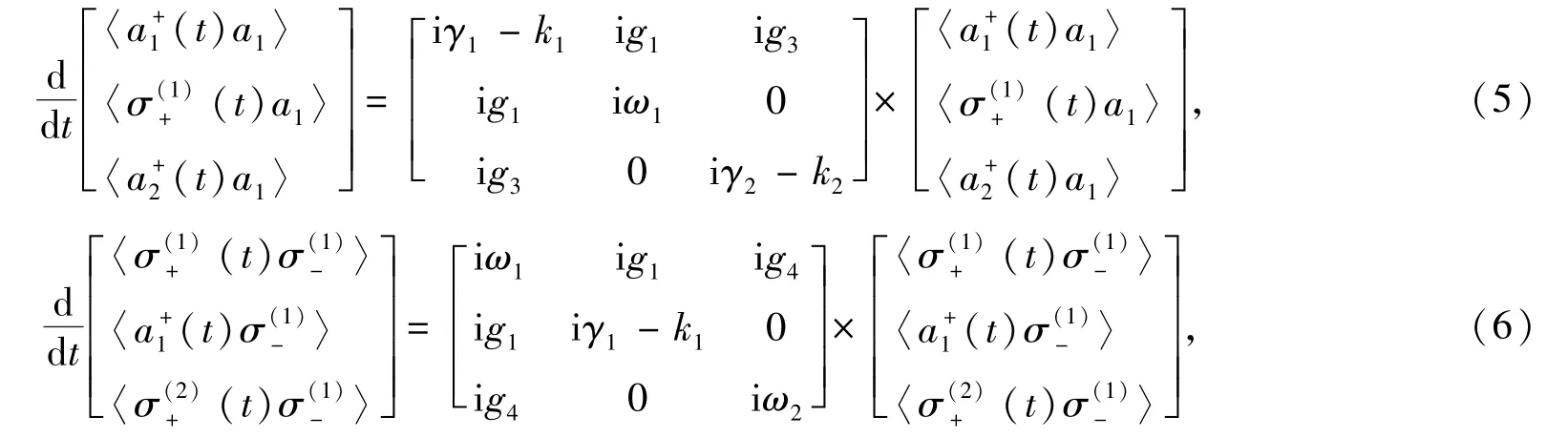
根据威纳-亨钦定理,该系统的辐射光谱[19]可按照下式计算:

3 辐射光场的量子效应
本节在考虑两等同双原子与两单模腔场耦合系数相同且两原子处于强耦合状态,即g=10k条件下,讨论了第一个腔场的平均光子数、二阶量子相关度、腔场Mandel's Q因子随时间的演化特性,得到辐射光场的量子效应。
取定两原子的跃迁频率为ω1=ω2≈1015Hz,腔场的跃迁频率为γ1=γ2≈1015Hz,腔场耗散系数为k1=k2≈109Hz,原子与腔场间耦合系数、两腔场间耦合系数、两原子间耦合系数为g1=g2= g3=g4≈1010Hz。
3.1 平均光子数的时间演化
下面根据双原子-双腔耦合系统的运动方程,通过数值模拟计算,分别讨论了在不同腔场耗散系数及腔场-腔场耦合系数的影响下,腔场平均光子数随时间的演化图像。

图2 (a)不同腔场耗散系数k1=k2=0.015,0.020, 0.025,0.030下的腔场平均光子数的时间演化规律;(b)原子间无耦合及强耦合对比时的腔场平均光子数的时间演化规律,其中嵌图为gt轴上106.5<gt<107间的一段曲线。Fig.2 (a)Mean photon number of the cavity field as a function of the scaled time(gt)for various values of the cavity dissipation coefficient,k1=k2=0.015, 0.020,0.025,0.030,respectively.(b)Mean photon number of the cavity field as a function of the scaled time(gt)for various values of the atom-atom coupling coefficient,g4=0,50.0,respectively.Inset shows the expanded view of the region of 106.5<gt<107 on the gt axis.
取腔场1的初始平均光子数为50,腔场2的初始平均光子数为100。图2(a)所示为在不同腔场耗散系数,即k1=k2=0.015,0.020,0.025, 0.030情况下,腔场1的平均光子数随时间gt的演化曲线。其中原子-腔场耦合系数、腔场-腔场耦合系数及原子-原子耦合系数为g1=g2=g3= g4=1.0。结果表明:无论腔场耗散系数如何变化,腔场平均光子数均由最初值50逐渐衰减最终趋近于0。而在衰减过程中伴随着周期性的量子起伏,即腔场平均光子数呈现Rabi振荡,说明二能级原子由激发态跃迁到基态向外辐射光子后,能够再次吸收满足一定频率条件的光子而返回到激发态,继续向外辐射光子。起初Rabi振荡比较剧烈,起振幅度较大;但随着时间的增加,拉比振荡幅度逐渐减小,最终曲线趋于平滑。在相同时间上,可以看出腔场耗散系数越大,则Rabi振荡幅度越小,且每次振荡时腔场平均光子数所达到的最大值也在逐渐减小,Rabi振荡趋于平缓的时间也在缩短,但腔场耗散系数的大小并不影响每次Rabi振荡的周期。图2(b)所示为原子间无耦合(g4=0)及强耦合(g4=50.0)时的腔场平均光子数的时间演化规律,其中腔场耗散系数为k1=k2=0.030,其余参数均与图2(a)相同。由图2(b)可以看出,无论原子间是否存在耦合,腔场平均光子数均出现Rabi振荡,似乎原子间是否存在耦合对Rabi振荡并无影响。但事实上并非如此。我们发现当原子间存在强耦合时,Rabi振荡的频率比原子间无耦合时明显加快,如图2(b)嵌图所示。该嵌图为取图2(b)的gt轴上在区间106.5<gt<107中的一段曲线(任一段都类似)。从嵌图中可以看出,当原子间无耦合时,腔场平均光子数在趋近于0的过程中几乎没有量子噪音出现;而当原子间存在强耦合时,腔场中平均光子数在趋近于0的过程中伴随着明显的量子噪音。
图3所示为不同腔场-腔场耦合系数影响下的腔场平均光子数随时间的演化规律。其中两腔场的耗散系数为k1=k2=0.05,原子-腔场耦合系数、原子-原子耦合系数为g1=g2=g4=1.0。图中为两腔场间耦合系数分别为g3=0.5,1.0, 1.5,2.0的情况。图3表明:无论腔场间耦合系数为何值,腔场平均光子数均随时间的延长而逐渐减少至0,此过程仍然伴随着Rabi振荡,且每一次振荡所达到的光子数最大值及振荡所持续的时间均不改变。但可以明显看出,随着腔场-腔场耦合系数的增大,振荡的周期在逐渐减小。
3.2 光场二阶量子相关度的时间演化
为了描述在已检测到一个光子或几个光子的情况下再次检测到另一光子的概率,定义光场二阶相关度g(2)(t):
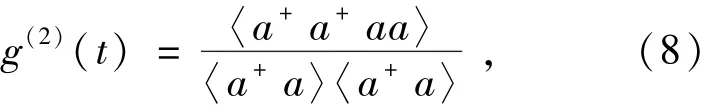
若g(2)(t)>1,说明光场中的光子间具有正关联,此时光场处于群聚状态;若g(2)(t)=1,说明光场中的光子间具有无关联,此时光场处于随机散布状态;若g(2)(t)<1,说明光场中的光子间具有负关联,此时光场处于反群聚状态,此类光场称为量子性光场,是量子光学所特有的特征场。
图4所示为不同腔场耗散系数,即k1=k2= 0.02,0.04,0.06情况下的腔场的二阶量子相关度随时间的演化图像。其中原子-腔场耦合系数、腔场-腔场耦合系数及原子-原子耦合系数为g1=g2=g3= g4=1.0。结果表明:初始时刻,g(2)(t)=0,光子数趋向不同时被检测到;随着时间的增加,二阶量子相关度出现周期性回复,且回复的幅度逐渐减小,最终曲线趋近于0变得平滑。从图中还可以看出,随着腔场耗散系数的增大,二阶量子相关度周期性回复所对应的最大值在逐渐减小,周期性回复所持续时间在减少。这表明腔场衰减程度越大,腔场二能级原子由激发态跃迁到基态检测到一个光子后,不易再次发生辐射跃迁。因此,系统光子的检测率降低,更加不容易检测到光子。但图像均表现为g(2)(t)<1,即光场表现出反群聚效应,此时光场具有明显的量子特性。
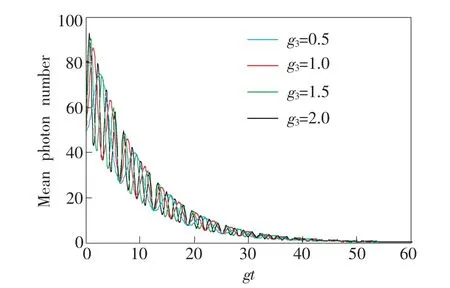
图3 不同腔场-腔场耦合系数g3=0.5,1.0,1.5,2.0情况下的腔场平均光子数的时间演化规律。Fig.3 Mean photon number of the cavity field as a function of the scaled time(gt)for various values of the cavity-cavity coupling coefficient,g3=0.5,1.0,1.5, 2.0,respectively.

图4 不同腔场耗散系数k1=k2=0.02,0.04,0.06情况下的腔场二阶量子相关度的时间演化规律。Fig.4 Quantum degree of second-order coherence g(2)(t)as a function of the scaled delay time(gt)for various values of the cavity dissipation coefficient k1=k2= 0.02,0.04,0.06,respectively.
图5所示为不同腔场耦合系数影响下的腔场二阶量子相关度随时间的演化规律。其中两腔场的耗散系数为k1=k2=0.05,原子-腔场耦合系数、原子-原子耦合系数为g1=g2=g4=1.0。结果表明:在相同时刻,两腔场间耦合系数越大,则相应的二阶量子相关度的值越大,变化的周期越短,即辐射光子越容易被检测到。在整个过程中,光场仍表现为反群聚状态。

图5 不同腔场-腔场耦合系数g3=0.5,1.0,1.5情况下的腔场二阶量子相关度的时间演化规律。Fig.5 Quantum degree of second-order coherence g(2)(t) as a function of the scaled delay time(gt)for various values of the cavity-cavity coupling coefficient g3=0.5,1.0,1.5,respectively.
3.3 M andel's Q因子的时间演化
为了研究量子光场区别于经典光场的统计特性,常引入Mandel's Q因子来描述光场的光子数分布特性,其定义为:
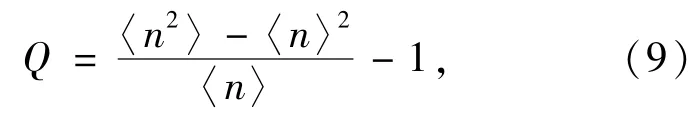
若Q>0,腔场的光子数分布统计为超泊松分布;若Q=0,腔场的光子数分布统计为经典的泊松分布;若Q<0,腔场的光子数分布统计为量子光学中特有的亚泊松分布,此时光场表现为量子特性。
图6为在不同腔场耗散系数下的腔场Mandel's Q因子的时间演化规律。其中原子-腔场耦合系数、腔场-腔场耦合系数及原子-原子耦合系数为g1=g2=g3=g4=1.0。结果表明:腔场Mandel's Q因子随时间的延长逐渐增加。在此过程中,Mandel's Q因子均由小于0最终趋近于0,说明腔场中的光子数分布由亚泊松分布统计逐渐趋于泊松分布,光场由量子性光场转变为相干光场。而Mandel's Q因子在变化过程中伴随着周期性振荡,说明腔场中的光场并不是线性变化的,这也是不同于经典光场的一个重要特性。若在相同时间上看,Mandel's Q因子随着腔场耗散系数的增大而逐渐增大,其偏离泊松分布的程度逐渐减小,光场越来越趋近于相干光场,量子特性逐渐削弱。

图6 不同腔场耗散系数k1=k2=0.015,0.020,0.025, 0.030情况下的腔场Mandel's Q因子的时间演化规律。Fig.6 Mandel's Q parameter as a function of the scaled time (gt)for various values of the cavity dissipation coefficient k1=k2=0.015,0.020,0.025,0.030, respectively.

图7 不同腔场-腔场耦合系数g3=0.5,1.0,1.5情况下的腔场Mandel's Q因子的时间演化规律。Fig.7 Mandel's Q parameter as a function of the scaled time (gt)for various values of thecavity-cavity coupling coefficient g3=0.5,1.0,1.5,respectively.
图7描绘了在腔场-腔场耦合系数不同时,腔场Mandel's Q因子随时间的演化规律。其中两腔场耗散系数均为k1=k2=0.05,原子-腔场耦合系数、原子-原子耦合系数为g1=g2=g4=1.0。结果表明:在不同腔场-腔场耦合系数下,腔场的Mandel's Q因子均随时间的延长而逐渐增大至0进而保持不变。在增加过程中仍伴随着量子振荡,且振荡幅度在逐渐减小,而腔场耦合系数仅影响其振荡周期。同时,Mandel's Q因子在变化过程中均为负值,说明光子数分布呈亚泊松分布,光场表现出量子特性。
4 辐射光场的谱结构
本节分别讨论了腔场跃迁频率、原子-腔场耦合系数对双原子-双腔耦合系统辐射光谱的影响,并将原子及腔场的谱结构进行了对比分析。取原子本征频率为ω0≈1014Hz,原子的跃迁频率为ω1=ω2≈1014Hz,腔场的跃迁频率为γ1=γ2≈1014Hz,腔场的耗散系数为k1=k2≈109Hz,原子和腔场间耦合系数、两腔场间耦合系数、两原子间耦合系数为g1=g2=g3=g4≈1010Hz。即g=10k为强耦合情况。
4.1 腔场跃迁频率影响下的谱结构
图8为不同腔场跃迁频率下的耦合系统的原子及腔场的辐射光谱随原子跃迁频率的变化曲线,γ1=9 998,9 999,10 000,10 001,10 002。结果表明:原子及腔场的谱线均出现3次起伏现象,即为Mollow三重峰结构,当且仅当腔场跃迁频率与原子本征频率共振,即γ=ω0=10 000时, Mollow三峰表现为对称性,其余情况均为非对称三峰。且随着腔场跃迁频率的增大,光谱整体均向低频段漂移。除此之外,还可以观察到当腔场跃迁频率越来越逼近于原子跃迁频率,即γ≈ω时,光谱峰值为Mollow三峰中的最大值,其余两峰峰值依次降低。对比可以发现,在相同条件下,原子中的光谱强度要高于腔场中的光谱强度。
4.2 原子-腔场耦合系数影响下的谱结构
图9所示为在不同原子-腔场耦合系数下,原子及腔场辐射谱的变化规律,g1=1.0,1.5, 2.0,2.5。结果表明:辐射光谱结构均出现对称的Mollow三重峰结构,且中间峰的位置固定不变(位于ω=ω0处),边峰位置均向两侧对称性移动,即高频段边峰向高频段移动,低频段边峰向低频段移动,并且移动距离随着原子-腔场耦合系数的增大而逐渐增大。在原子的辐射谱中,随着原子-腔场耦合系数的增大,中峰的高度呈逐渐递增趋势,而边峰的高度则呈现逐渐递减的趋势。在腔场的辐射谱中,其增减趋势恰恰相反,即中峰的高度随着原子-腔场耦合系数的增大而逐渐递减,边峰的高度则随着原子-腔场耦合系数的增大而逐渐递增。对比图9(a)、(b)仍可看出:原子中的光谱强度仍强于腔场中的光谱强度。

图8 腔场跃迁频率影响下的原子(a)和腔场(b)的辐射光谱随原子跃迁频率的变化关系Fig.8 Emission spectra of the atom(a)and cavity filed (b)as a function of the atomic transition frequency under the influence of the cavity field transition frequency

图9 原子-腔场耦合系数影响下的原子(a)和腔场(b)的辐射光谱随原子跃迁频率的变化关系Fig.9 Emission spectra of the atom(a)and cavity filed (b)as a function of the atomic transition frequency under the influence of the atom-cavity coupling coefficient
5 结 论
在考虑原子-原子间耦合的条件下,研究了双原子-双腔耦合体系的量子特性及系统光谱结构。结果表明:系统平均光子数呈现出Rabi振荡形式,光子数呈亚泊松分布且光场具有反聚束效应。而Rabi振荡幅度随腔场耗散系数的增大呈递减趋势,振荡趋于平缓时间也在逐渐缩短;腔场-腔场耦合系数影响Rabi振荡周期,逐渐增大两腔场间耦合系数,其振荡周期在逐渐缩短。这说明减小腔场耗散系数,增大两腔场间耦合强度,体系量子特性愈加明显。此外,通过分析耦合系统的光谱结构,发现原子及腔场辐射光谱均呈现出Mollow三重峰结构,且原子的光谱强度要高于腔场中光谱强度。
[1]Jaynes E T,Cummings FW.Comparison of quantum and semi-classical radiation theorieswith application to the beam maser[J].Proc.IEEE,1963(51):89-109.
[2]Rosenhouse A.On the squeezing of coherent states by themultiphoton Jaynes-Cummings Hamiltonian with an intensity dependent coupling[J].J.Mod.Opt.,1991,38(2):269-286.
[3]Agarwal G S.Vacuum-field Rabi splitting inmicrowave absorption by Rydberg atoms in a cavity[J].Phys.Rev.Lett., 1984,53(18):1732-1734.
[4]Peter E,Senellart P,Martrou D,et al.Exciton-photon strong-coupling regime for a single quantum dot embedded inmicrocavity[J].Phys.Rev.Lett.,2005,95(6):067401-1-4.
[5]Eberly JH,Narozhny N B,Sanchez-Mondragon JJ,etal.Periodic spontaneous collapse and revival in an simple quantum mode[J].Phys.Rev.Lett.,1980,44(20):1323-1326.
[6]Knight P L,Reamore PM.Quantum origin of dephasing and revivals in the coherent state Jaynes-Cummingsmodel[J]. Phys.Rev.A,1982,26(1):676-679.
[7]Martini U,Ginzel C,Schenzle A,etal.Optical bistability and nonclassical photon counting statisticswith few atom[J]. Opt.Commun.,1993,102(3):379-390.
[8]Hekmatara H,Tavassoly M K.Sub-poissonian statistics,population inversion and entropy squeezing of two two-level atoms interaction with a single-mode binomial field:Intensity-dependent coupling regime[J].Opt.Commun.,2014,319: 121-127.
[9]Thompson R J,Rempe G,Kimble H J.Observation of normal-mode splitting for an atom in an optical cavity[J].Phys. Rev.Lett,1992,68(2):1132-1135.
[10]Rempe G,Walther H,Klein N,etal.Observation ofquantum collapse and revival in a one-atom master[J].Phys.Rev. Lett.,1987,58(4):353-356.
[11]Tavis M,Cummings FW.Exact solution for an N-molecule-radiation-field Hamiltonian[J].Phys.Rev.Lett.,1968, 170(2):379-384.
[12]Ji Z L,Gao SY.Two-photon scattering by a cavity-coupled two-level emitter in one-dimensional waveguide[J].Opt. Commun.,2011,285(6):1302-1307.
[13]Obada A SF,Ahmed M M A,Khalil EM,etal,Entangled two two-level atoms interactingwith a cavity field in the presence of the Stark shift terms[J].Opt.Commun.,2013,287(5):215-223.
[14]Liang M L,Yuan B,Zhang JN,et al.Complete entanglement transfer between light and qubits[J].Opt.Commun., 2009,283(1):203-208.
[15]FaghihiM J,Tavassoly M K,Hatami M,et al.Dynamics of entanglement of three-level atom in motion interaction with two coupled modes including parametric down conversion[J].Phys.Rev.A,2014,407:100-109.
[16]Feng C,Sa CE F,LiH X.Entanglementofan atom interactingwith Glauber-Lachs state inmultiphoton Jaynes-Cummings model[J].Acta Optica Sinica(光学学报),2013,33(5):0527001-1-6(in Chinese).
[17]Song L J,Yan D,Li Y D,et al.Properties of spin squeezing in the quantum chaotic system[J].Chin.J.Lumin.(发光学报),2007,28(3):336-340(in Chinese).
[18]LiW Z,Zhang C L,Shen L T,et al.Entanglement dynamics and maintenance for two atoms in coupled cavities[J].Opt.Commun.,2014,315:213-219.
[19]Tan R,Li C X,Ficek Z,et al.Squeezed single-atom laser in a photonic crystal[J].Phys.Rev.A,2008,78(2): 023833-1-5.
Quantum Properties and Spectra of A Pair of Equivalent Atom s Jaynes-Cumm ings M odel
ZHANG Dan-feng,LYU Shu-chen*
(Key Laboratory ofPhotoelectric Bandgap Materials,Ministry of Education,Harbin Normal University,Harbin 150025,China)
*Corresponding Author,E-mail:hsdlsc63@126.com
Based on the all-quantum theory,the system which includes two double-level atoms interacting with two single-mode cavity fields separately was studied.With making the Markoff and the rotating-wave approximations,using quantum master equation and the numerical simulation,we investigated the influence of the cavity dissipation coefficient and the cavity-cavity coupling coefficient on the mean photon number distribution under the unsteady situation.In the meantime,we discussed how the Mandel's Q parameter and the second-order coherence were changing,and then analyzed the quantum effects of the system.Besides that,we analyzed the spectra of the atoms and the cavities.The results show that the system quantum properties becomemore obvious by reducing the cavity dissipation coefficient and increasing the coupling coefficient between cavities.The system spectra present Mollow three peak structure,and the atomic emission spectrum intensity is greater than the cavity field spectrum intensity.When the atomic transition frequency and the cavity transition frequency is near resonance,the Mollow peak is the highestof the three peaks.In addition,the spectrum intensity of the atomic middle peak increases with the increasing of the atom-cavity coupling coefficient,and the spectrum intensity of the cavitymiddle peak is quite opposite.
quantum master equation;double coupling two-level system;sub-Poisson distribution;anti-bunching effect;spontaneous emission spectrum

张丹凤(1990-),女,黑龙江哈尔滨人,硕士研究生,2013年于哈尔滨师范大学获得学士学位,主要从事量子光学理论的研究。E-mail:zdf7046@163.com

吕树臣(1963-),男,黑龙江哈尔滨人,教授,博士生导师,2002年于中国科学院长春光学精密机械与物理研究所获得博士学位,主要从事量子光学及固体发光方面的研究。E-mail:hsdlsc63@126.com
O562
A
10.3788/fgxb20153612.1375
1000-7032(2015)12-1375-08
2015-09-05;
2015-10-10
哈尔滨市科技局科技创新人才研究基金(2014RFXXJ091)资助项目

