第二类曲面积分易错题分析研究
景慧丽
(第二炮兵工程大学 理学院,陕西 西安 710025)
第二类曲面积分易错题分析研究
景慧丽
(第二炮兵工程大学 理学院,陕西 西安 710025)
正确地计算第二类曲面积分既是本科生必须熟练掌握的也是全国硕士研究生入学考试的重要内容之一.但是,大部分学员在计算第二类曲面积分时经常出错.学员解题过程中经常出现的错误类型归纳起来主要有四种:一是找错积分曲面;二是不注意曲面的侧;三是误用对称性;四是错用高斯公式.文中就各种错误类型给出了相应的例题,并重点对错解进行了分析,最后给出了正确解法和注意事项.
第二类曲面积分;易错题;错解分析
0 引言
第二类曲面积分是《高等数学》课程和《数学分析》课程中一个非常重要的概念,而关于第二类曲面积分的计算更是重点中的重点,也是难点中的难点.初学者甚至是有些复习考研的学员经常是遇到第二类曲面积分的计算问题就束手无策、无从下手.有的学员虽然知道用什么方法计算,但是经常算错;有时即便结果是正确的,计算过程却是错误的.为了帮助学员掌握第二类曲面积分的计算方法,并能熟练、正确地计算第二类曲面积分,笔者结合教学实践就学员在解题过程中经常出现的错误进行了分析,归纳了学员解题过程中所出现错误的类型,并重点分析了出错的原因.常见的错误类型主要有以下几种.
1 找错积分曲面
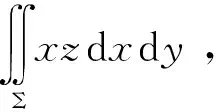
2 不注意积分曲面的侧
计算第二类曲面积分最基本的方法就是把积分曲面投影到坐标面上,然后把第二类曲面积分转化成二重积分来计算,只是这个二重积分前有个正负号.例如[1]87-90,若积分曲面Σ是由方程z=z(x,y)所给出的,Σ在xoy坐标面上的投影区域为Dxy,函数z=z(x,y)在Dxy上具有一阶连续偏导数,函数R(x,y,z)在Σ上连续,则
当Σ取上侧(即曲面Σ的法向量与z轴正向的夹角为锐角)时,(1)式右端取“+”号;当Σ取下侧(即曲面Σ的法向量与z轴正向的夹角为钝角)时,(1)式右端取“-”号.但是,大部分学员往往忽略了这个正负号.
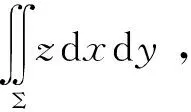
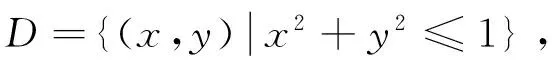

3 误用对称性
利用对称性计算定积分、二重积分、三重积分、第一类曲线积分和第一类曲面积分都是一种非常巧妙的方法,所以,大部分学员遇到第二类曲面积分的计算就会习惯定式,也直接利用对称性来计算.
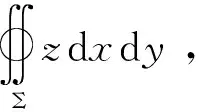
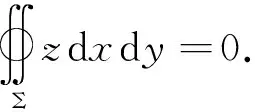
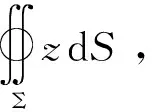
若积分曲面Σ关于yoz坐标面对称,Σ1表示x≥0的部分,且Σ和Σ1所取的侧一致,则
若积分曲面Σ关于xoz(或xoy)坐标面对称,被积函数P,Q,R关于y(或z)有奇偶性,则第二类曲面积分具有相似的结论,这里不再赘述.
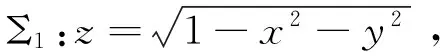
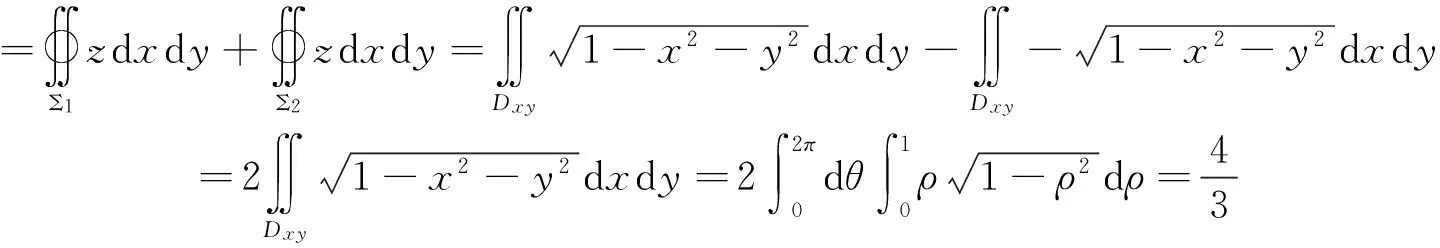
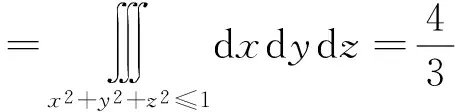
注2:第二类曲面积分的对称性是比较麻烦的,所以不鼓励学员利用对称性来计算第二类曲面积分,建议学员先把第二类曲面积分转化为二重积分,在计算二重积分的过程中再考虑利用对称性,因为二重积分的对称性是学员比较熟悉的.
4 错用高斯公式
高斯公式是[2]229:设空间闭区域Ω是由分片光滑的闭曲面Σ所围成,函数P(x,y,z)、Q(x,y,z)、R(x,y,z)在Ω上具有一阶连续偏导数,则有
这里Σ是Ω的整个边界曲面的外侧.
高斯公式为计算第二类曲面提供了一种有效方法,使用高斯公式时必须满足高斯公式的三个使用条件:a)函数P(x,y,z)、Q(x,y,z)、R(x,y,z)必须在Σ所围区域Ω上具有一阶连续偏导数;b)曲面Σ必须封闭;c)曲面Σ取外侧.但是,大部分学员经常不管是否满足高斯公式的使用条件,就直接使用高斯公式,学员常犯的错误主要有三种:一种是积分曲面Σ取内侧直接利用高斯公式;第二种是对非封闭曲面直接利用高斯公式;第三种是在积分曲面Σ所围区域Ω上存在奇点(使函数P、Q、R无定义的点或不具有一阶连续偏导数的点统称为奇点)时也直接利用高斯公式.下面分别举例说明:
4.1 积分曲面取内侧直接利用高斯公式
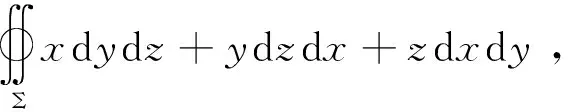
[错解] 记Σ所围区域为Ω,则由高斯公式得
原式
[错解分析] 上述解法错在三重积分前少了一个负号,因为高斯公式成立的条件之一是积分曲面Σ取外侧,且注意到第二类曲面积分的值与积分曲面的侧密切相关,侧改变积分值也改变.所以,如果积分曲面Σ取的是内侧,则应在公式的一端加上一个负号,即此时高斯公式应为:
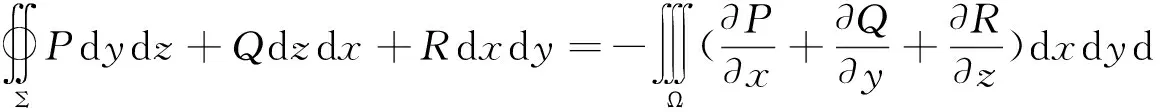
本解法忽略了高斯公式中积分曲面取外侧这个条件,所以是错误的.
[正确解法] 记Σ所围区域为Ω,则由高斯公式得
原式
注3:使用高斯公式时,积分曲面Σ要取外侧,如果Σ取内侧,需要在公式一端加上负号.
4.2 非封闭曲面直接利用高斯公式
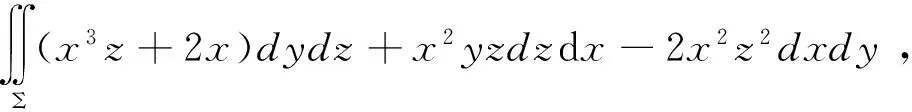
[错解] 记Σ所围区域为Ω,则由高斯公式得
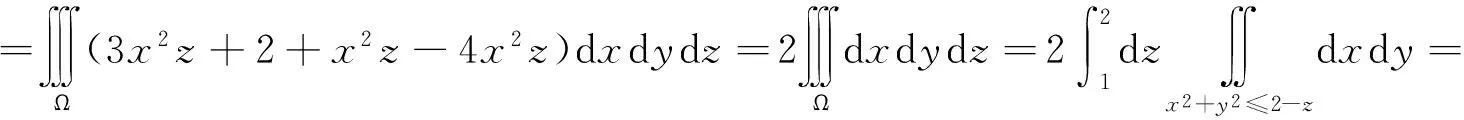
[错解分析] 上述解法错在直接利用高斯公式来计算,因为使用高斯公式时积分曲面Σ必须封闭,这里的Σ显然是不封闭的,所以是不能直接利用高斯公式来计算.
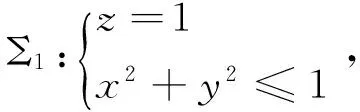
原式
注4:使用高斯公式计算第二类曲面积分时积分曲面Σ必须封闭,如果Σ不封闭,必须先补充有向曲面使其封闭,然后再使用高斯公式.补充有向曲面的一般原则是通常取平行于坐标面的有向平面,该有向平面的侧要与已知的积分曲面的侧保持一致.另外,切记计算原曲面积分时还要把所补充的有向曲面上的曲面积分减去.
4.3 存在奇点直接利用高斯公式
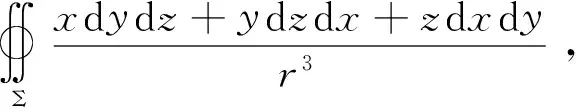
原式
其中Ω:x2+y2+z2≤a2.
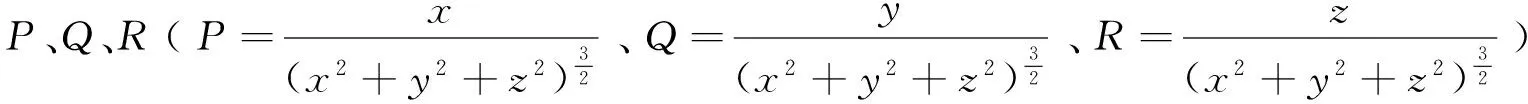
[正确解法] 原式
令P=x、Q=y、R=z,则由高斯公式得
原式
其中Ω:x2+y2+z2≤a2.
注5:使用高斯公式时,函数P、Q、R必须在Σ所围区域Ω上具有一阶连续偏导数,如果在Σ所围区域Ω上存在奇点,一般是需要把奇点挖去,在挖去奇点的复连通域上再使用高斯公式,挖奇点的一般原则是根据被积函数的特征来挖.例如,若例5中积分曲面Σ是包围原点的某一光滑闭曲面,则需要在Σ内作有向曲面Σ1:x2+y2+z2=ε2(ε要足够小),然后在Σ和Σ1所围复连通域上再使用高斯公式.其实,注意到曲面积分具有一个很好的性质,可以把积分曲面的方程代入到被积函数中,如果先把积分曲面的方程代入到被积函数中就可以大大简化计算.例如例5所给的正确解法就是利用了该性质,首先把积分曲面Σ的方程x2+y2+z2=a2代入到被积函数中,此时新的曲面积分就满足高斯公式的使用条件了,大大简化了曲面积分的计算.
5 结语
以上就是学员们在计算第二类曲面积分时经常出现的错误.其实只要学员真正理解了第二类曲面积分的概念,掌握了第二类曲面积分的计算方法,上述错误是完全可以避免的.在教学过程中教员也应允许学员出错,学员对概念理解有偏差、解题过程出现错误都是正常的,都是符合实际情况的,如果学员不出错反而是不符合常理的.另外,教员要正确看待这些错题资源,这些资源都是非常宝贵的教学资源,因为心理学家盖耶说过:“谁不考虑尝试错误,不允许学生犯错误,就将错过最富成效的学习时刻”[4]372-373.在教学中,教员要主动挖掘学员错题中的“闪光点”,及时进行探究、分析和讲评,这不但可以为学员创造新的学习机会,而且还可以培养学员的问题意识,培养学员发现问题、解决问题的能力.
[1] 景慧丽,张 辉.第二类曲面积分的计算方法[J].高等数学研究,2011,14(4).
[2] 同济大学应用数学系.高等数学(下)[M].6版.北京:高等教育出版社,2007.
[3] 张天德,蒋晓芸.Б.П.吉米多维奇高等数学习题精选精解[M].1版.济南:山东科学技术出版社,2010.
[4] 钱怡杰.基于错题的高三基础会计教学探究[J].经营管理者,2015(2).
[责任编辑 迎客松]
On the Second Type of Surface Integral Easy Wrong Topic
JING Huili
(SchoolofScience,theSecondArtilleryEngineeringUniversity,Xi’an710025,China)
Correctly calcuating the second type of surface integral is not only a skill undergraduate students must master, but also an important content of the national master’s degree students’ entrance examination. But most of the students often make mistakes when calculating the surface integral. The error that the students made in the process of problem solving is concluded in this paper. There four kinds of common errors: the first is the wrong integral surface; the second is not paying attention to the side of the surface; the third is the misuse of symmetry; the fourth is wrong use Gauss formula. Furthermore, some corresponding examples are given for each type of error, the right solution is analyzed, and the correct solution and some matters needing attention are discussed.
the second type of surface integral;easy wrong topic;error analysis
2015-07-28
第二炮兵工程大学2014年度教育教学立项课题(项目编号:EPGC2014023)
景慧丽(1983- ),女,河南平顶山人,第二炮兵工程大学讲师,硕士,主要从事高等数学教学研究。
1671-8127(2015)05-0004-05
O172.4-4
A

