基于离散裂缝的致密油藏重复压裂数值模拟研究
马 康,姜汉桥,方文超,赵 林,张振涛,郭 亮
(中国石油大学石油工程教育部重点实验室,北京昌平 102249)
基于离散裂缝的致密油藏重复压裂数值模拟研究
马 康,姜汉桥,方文超,赵 林,张振涛,郭 亮
(中国石油大学石油工程教育部重点实验室,北京昌平 102249)
致密油藏储层物性差,大多采用压裂方式开发,当产量下降时需要重复压裂进行增产。建立了基质与人工裂缝相互耦合的致密油藏重复压裂渗流模型,采用离散裂缝模型对压裂形成的人工裂缝进行分析,用三种网格划分体系剖分基质系统、初次压裂裂缝、重复压裂裂缝系统。研究结果表明:裂缝长度和导流能力对重复压裂后的产能影响较大,在生产实际中应采用与储层性质匹配的裂缝长度和导流能力;启动压力梯度对于致密油藏的产能影响明显,在生产设计时需要重点考虑。
致密油藏;重复压裂;数值模拟
1 前言
致密油藏储层孔喉结构复杂,渗透率极低,流体渗流阻力大[1-3],流体流动的非线性程度增强,不可忽略启动压力梯度对产能的影响。致密油藏采用压裂方式开发,但由于缝内支撑剂长期受挤压发生变形,造成裂缝堵塞等原因,人工裂缝的导流能力会不断变差,需要采用重复压裂使油井提高产量。由于初次压裂裂缝的影响,重复压裂的新缝将在未泄油区发生延伸[4-9]。前人对于气井的重复压裂做了相应的研究[10-11],但对于致密油藏的重复压裂的研究较少,特别是在数值模拟方面的研究还不够深入。本文主要建立了致密油藏两维两相的非线性渗流与离散裂缝中一维两相达西渗流耦合的模型。根据在基质和裂缝接触壁面位置上压力和相互之间交换的窜流量相等的条件,建立两个系统间流体交换的内边界条件[12-16]。根据对称性原则,选取三角井网(交错井网)中对角上的两口油水井作为计算单元体进行研究,通过建立模型可以得出相应的压力、饱和度的分布情况以及在不同条件下产液量的变化情况,从而为致密油藏重复压裂生产方式优化提供理论指导。
2 致密油藏重复压裂的渗流模型
2.1 物理模型
将实际地层中存在的人工裂缝进行简化,其中重复压裂的裂缝简化为相互垂直的裂缝系统,如图1所示。图1中a表示在初次压裂裂缝存在的条件下,井周围一定椭圆区域内发生应力反转,即最大主应力与最小主应力方向转换,进行重复压裂时,在应力重定向区内,裂缝的起裂角与初次压裂裂缝呈90°角,当裂缝超出应力重定向区后,继续沿初始地应力状态进行延伸。b表示将地层中的初次和重复压裂的裂缝进行简化处理的模型,将重复压裂裂缝分成相互垂直的两段:垂直段、水平段。

图1 物理模型
2.2 模型假设
(1)基质中流体流动为考虑启动压力梯度的非线性渗流,并且忽略重力、毛管力的影响;
(2)油藏岩石和流体微可压缩,地层均质;
(3)三角井网生产,油水井均采用定压生产工作制度,仅油井进行重复压裂;
(4)人工裂缝为有限导流的垂直缝;
(5)裂缝中的流动为达西渗流。
2.3 模型建立
(1)基质区域压裂模型为:
(1)
式中:ρo为油相的密度,g/cm3;K为地层渗透率,10-3μm2;Kro为油相相对渗透率;μo为油相的黏度,mPa·s;po,w为油水相的压力,MPa;Go为油相的启动压力梯度,MPa/m;qo为单位地层体积的产量,m3;δnf(0-1)表示基质是否与第n条裂缝相邻;qonf为与第n条裂缝相邻的基质窜流量,m3;φ为孔隙度,%;So为油相饱和度,%;Pin为注水井注入压力,MPa;Pwf为生产井井底流压,MPa;Pi为原始地层压力,MPa;Swi为原始地层饱和度,%。
(2)裂缝区域压裂模型为:
(2)
式中:Kf为裂缝的渗透率,10-3μm2;qfo为单位地层体积的产量,m3;δnf(0-1)表示基质是否与第n条裂缝相邻;qonf为与第n条裂缝相邻的基质的窜流量,m3;δnfkf(0-1)函数表示第n条裂缝是否与第k条裂缝交叉;So为油相饱和度,%;pf为裂缝中的压力,MPa;xf为裂缝长度,m;wf为裂缝宽度,m;Kf为裂缝渗透率,10-3μm2;h为裂缝高度,m。
(3)关联条件:与裂缝接触的基质流出量与流入裂缝的流量相等。
(3)

2.4 计算单元选取与网格划分
图2-a表示选取三角井网中对角上的两口井研究,并且仅对油井进行重复压裂。在图2-b中,点A表示实际空间中两条裂缝的交点,为同一个点,点B是两次压裂形成的人工缝与生产井的交点,两条人工缝并不相交。因此需要将初次压裂的裂缝和重复压裂的裂缝看作两个体系。对初次压裂裂缝采用一维的网格如图2-c所示;对重复压裂裂缝采用二维“缝网”的网格体系,此时的“缝网”与常规的缝网不同,仅仅由两条相互垂直的水平段和转向段(线段AB)组成,该网格体系中只有实线位置是有效网格,其他位置为无效网格,如图2-d所示。
2.5 基质-裂缝的流量与产能
根据基质中的流出量与裂缝中的流入量相等的条件,将基质与裂缝联系起来。并且流量项采用隐式处理。
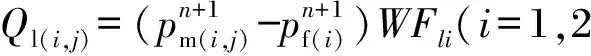
(4)


图2 计算单元与网格划分
因此生产井的产能由三部分组成:基质流到井筒中的量、初次压裂裂缝流到井筒的量、重复压裂裂缝流到井筒中的量,产量项均采用隐式处理。
基质中产液量的计算公式为:
(5)
式中:re边界的半径,m;rw井筒半径,m。
致密油藏重复压裂井的产能公式:
Q=4Qm+2Qif+2Qrf
(6)
式中,Qm、Qif、Qrf分别表示由基质、初次压裂裂缝、重复压裂裂缝所提供的液量,m3。
3 产能影响因素分析
结合某油藏储层参数,利用上述重复压裂渗流模型分析不同的油藏及裂缝参数对重复压裂油井产能的影响效果。
分别分析重复压裂的转向段、水平段长度,裂缝导流能力对产能的影响。从图3和图4可以看出,在三角井网油水井定压生产的条件下,重复压裂转向段和水平段的裂缝长度对生产动态的影响较大。在生产初期,裂缝的长度对产量影响较大,但长度增大到一定阶段后,产量没有明显的增加。

图3 不同转向段长度与产液量的关系
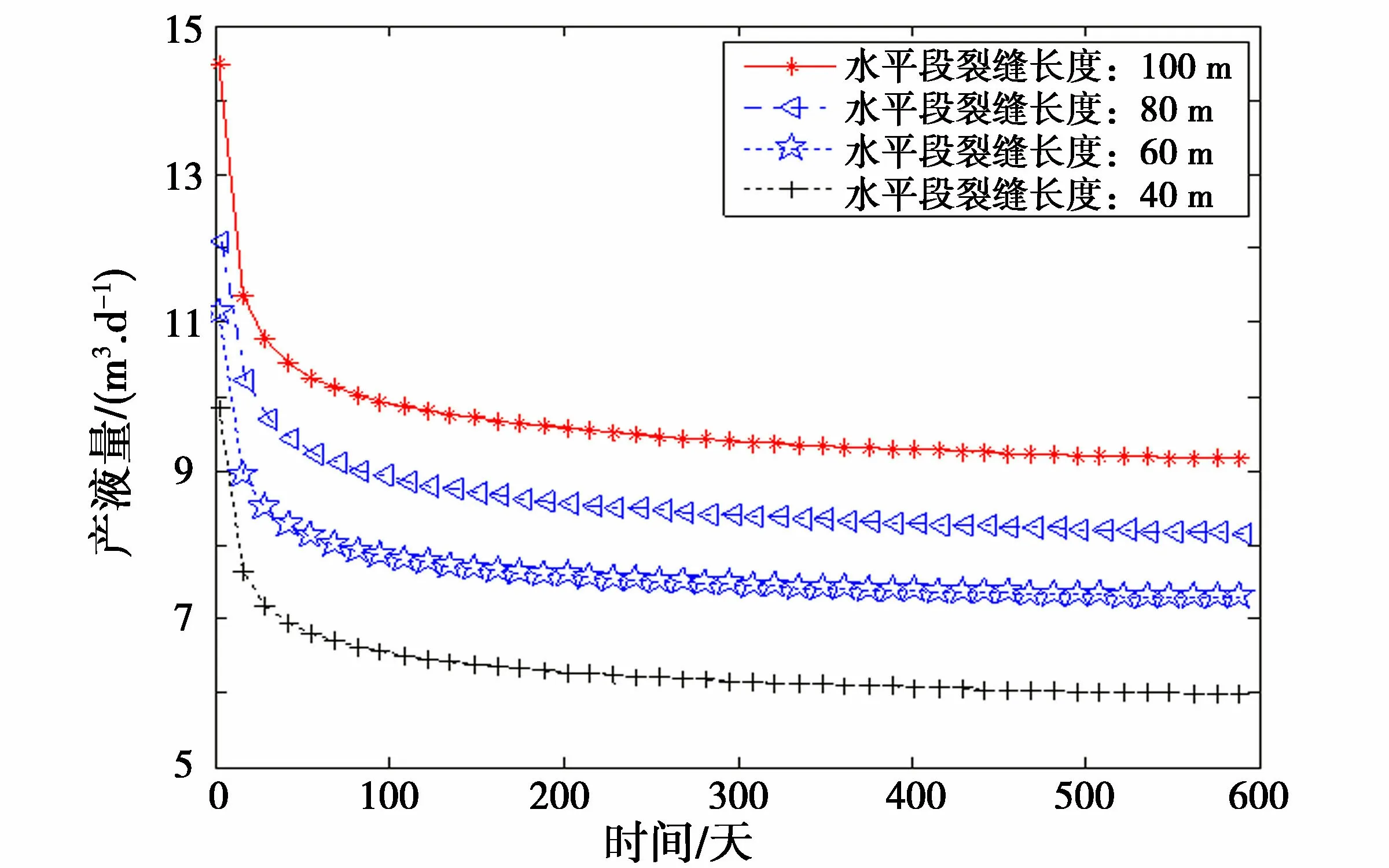
图4 不同水平段长度与产液量的关系
从图5可以看出,重复压裂裂缝导流能力在生产初期对油井产能的影响较明显,导流能力对产量影响较大,但在生产的后期,不同导流能力的裂缝的产能基本一致。通过图中的对比可以得到,当导流能力为20 μm2·cm时,生产中可获得较大的产能。
4 结论
(1)建立了致密油藏重复压裂模型,其中,基质为系统考虑启动压力梯度的两维两相非线性渗流,离散裂缝系统为一维两相达西渗流耦合模型,采用隐式处理裂缝-基质窜流关系。

图5 不同导流能力与产液量的关系
(2)采用离散裂缝的处理方法对于重复压裂中的基质-裂缝流动动态、交叉裂缝的流动关系以及产能变化形式的描述更加精细化,计算结果更加可靠。
(3)致密油藏重复压裂转向裂缝段和初始裂缝长度对井网产能影响较大,随裂缝长度增加,井网产量增加,但是增加的幅度逐渐减小。裂缝导流能力在生产初期对产量影响效果明显,后期没有太大的影响,需要在生产中优选合理的导流能力。
[1] 邹才能,朱如凯,吴松涛,等.常规与非常规油气聚集类型、特征、机理及展望[J].石油学报,2012,(2):173-187.
[2] 翁定为,姚飞,李阳,等.重复压裂裂缝转向时油藏数值模拟研究[J].石油钻采工艺,2006,(6):65-65.
[3] 王青青,常笃. 人工裂缝井数值模拟网格技术研究[J].石油化工应用,2009,(5):58-60.
[4] 胡永全,林辉,赵金洲,等.重复压裂技术研究[J].天然气工业,2004,24(3):72-74.
[5] 马新仿,樊凤玲,张守良.低渗气藏水平井压裂裂缝参数优化[J].天然气工业,2005,(9):61-63,155.
[6] 张化强. 基于非线性渗流的低渗裂缝性油藏数值模拟研究[D].北京:中国石油大学,2011.
[7] 张宾. 低渗透油藏数值模拟技术研究[D].北京:中国石油大学,2009.
[8] 任岚,胡永全,赵金洲, 等.重复压裂气井产能模拟研究[J].石油钻探技术,2006,34(1):53-55.
[9] 任岚,胡永全,赵金洲,等.重复压裂井产能评价方法研究[J].石油地质与工程,2005,19(6):54-56.
[10] Hagoort J, Weatherill B D, Settari A. Modeling thepropagation of waterflood-induced hydraulic fractures[J]. Society of Petroleum Engineers Journal,1980,20(4):293-303.
[11] 陈光俊,张汉荣,Chris A.Wright.水力压裂重定向的可能性和重要性[J].勘探地球物理进展,2002,(1):50-54.
[12] 姚健欢,侯冬冬,刘娟,等.考虑介质变形和启动压力梯度的低渗压裂气井产能分析[J].科学技术与工程,2014,(33):192-195.
[13] 孙庆友.大庆油田低渗透裂缝性油藏重复压裂造缝机理研究[D].黑龙江大庆:东北石油大学,2011.
[14] 牛栓文,崔传智,陈翰.低渗透油藏压裂水平井产能预测研究[J].科学技术与工程,2013,(3):584-587.
[15] 牟松茹,张士诚,张平.考虑启动压力梯度的致密气藏压裂井产能分析[J].科学技术与工程,2011,(34):8434-8437.
[16] 何艳青,王鸿勋.用数值模拟方法预测压裂井的生产动态[J].石油大学学报(自然科学版),1990,14(5):16-25.
编辑:李金华
1673-8217(2015)04-0128-04
2015-03-22
马康,1991年生,2014毕业于中国石油大学(华东)石油工程专业,在读硕士生,从事油气田开发方向研究。
国家重点基础研究发展计划(973)项目子课题“致密油高效开发油藏工程理论与方法研究”(2015250905)。
TE357
A

