在SOPC上实现Mean Shift的改进算法※＊

信 科

（滨州学院 信息工程系，滨州256600）

引 言

Mean Shift算法[1]是一种基于密度梯度的无参数估计方法，是模板匹配跟踪算法中的一种主流算法，在2003年由Comaniciu D引入到目标跟踪领域，因其收敛速度快、计算量小、实时性好引起了人们的广泛关注。它利用图像中像素建立加权直方图作为目标特征，具有一定的抗遮挡、抗形变的能力，但对尺度变化目标的跟踪性能不佳。目前的研究多基于软件仿真[2-4]，对于硬件实现的研究并不多。

目前的实现方法是基于DSP＋FPGA设计[5]，以DSP为主、FPGA为辅。在参考文献[5]中，DSP完成算法主流程的计算，FPGA仅负责算法直方图统计部分和外围电路。因为Mean Shift算法基于浮点运算，不利于FPGA编程实现，FPGA＋DSP协同实现时，系统的处理时间最快达到20 ms左右，无法满足实时性更高的场合，如帧频为100 fps的高速信号处理系统。

本文提出一种基于SOPC实现Mean Shift算法的新方法，在单片FPGA上利用SOPC技术搭建算法的硬件平台，软硬件协同工作实现算法给出了实验分析和结论。

1 Mean Shift算法简介

Mean Shift算法是一种半自动的目标跟踪算法，其跟踪框图如图1所示。在起始帧手动标定跟踪窗的中心和位置，计算得到核函数加权的直方图分布（即目标模板）；在当前帧保持上一帧的跟踪位置不变，计算得到候选目标模板；以目标模板和候选模板的最相似为原则，使目标窗口沿偏移矢量（即梯度变化最大的方向）移动，最终定位目标的真实位置。

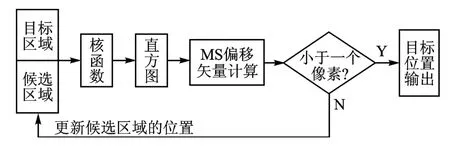
图1 Mean Shift算法的跟踪框图

Mean Shift算法主要包括下面4个计算步骤。

1.1 核函数k（x）的计算

其中，｛zi｝i＝1...n表示跟踪窗口内的任一像素点（xi，yi），z0表示窗口中心 （xcenter，ycenter）。

1.2 目标模型或候选模型的建立

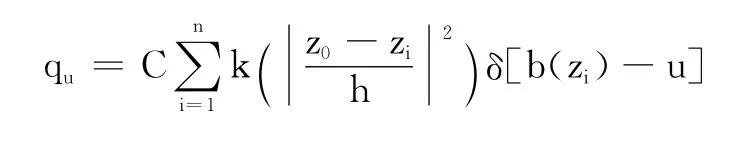
或

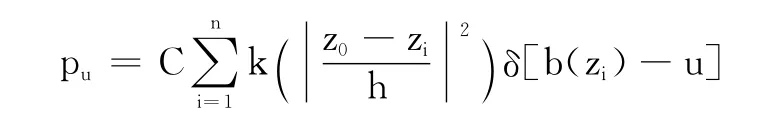
其中，冲激函数δ[b（zi）-u]的作用是判断b（zi）的灰度值是否属于第u个量化值，为归一化常数以保证所有量化值的概率和为1。

1.3 偏移矢量的权重

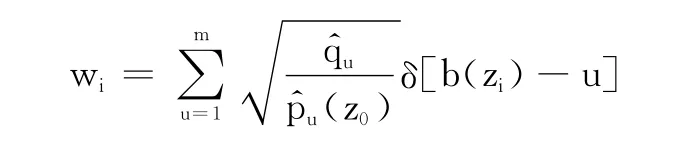
由权重计算公式可以得出下面的结论：每个像素点zi对应的偏移矢量的权重，由其对应的量化值在目标模型和候选模型中的概率决定，与zi的位置无关。

1.4 偏移矢量

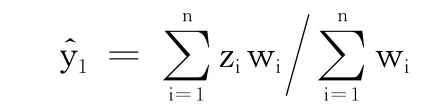
[6]证明了Mean Shift迭代过程对于目标跟踪的应用具有空域位置上的收敛性，表示目标下一个跟踪位置相对当前跟踪位置的偏移矢量。

2 改进的Mean Shift目标跟踪算法

由Mean Shift算法的计算步骤可以看出，其采用浮点运算，不利于用FPGA实现。下面主要介绍对各步骤的优化。

2.1 核函数k（x）的优化

从核函数的表达式可以看出，对于位于带宽内的像素点，k（x）与相对距离的平方成反比；带宽外的像素点，k（x）为0。核函数计算中涉及浮点数据的平方运算，单个时钟周期内不可能完成，因此，进行下面的改进，保证单个时钟周期能完成计算过程。

因为：

所以有：

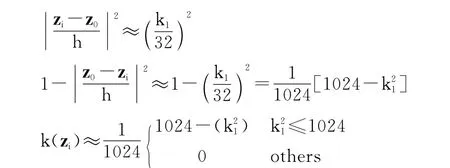
由变化后的公式可以看出，对跟踪窗口的带宽32等分和对相似距离求近似后，浮点运算变为整形运算。因为k1的取值范围已知，k21的取值可以事先求得，而1/1024为所有k（x）公因子，可以先不考虑，则在计算过程中只涉及比较和减法运算，FPGA能在单个时钟周期内完成计算。与列积分直方图加权类似，在核函数优化过程中采取了近似，使浮点运算变为整形运算。表1给出了使用带宽不同的核函数时，近似对匹配度的影响。其中，hx、hy为带宽，相似系数表示核函数分别采用浮点运算和整数运算求得的两个加权直方图的匹配度。可以看出，经近似后匹配度仍保持在0.999以上。

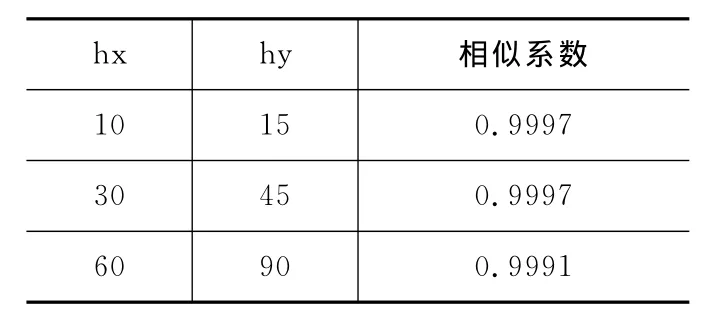
表1 整形近似后的相似系数

2.2 模型的优化

目标模型和候选模型的计算步骤完全一致，在此，以目标模型为例进行介绍，候选模型的优化与此类似。

目标模型的公式为：

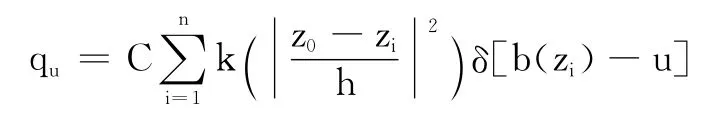
可以看到，计算结果qu是与量化等级u对应的函数，是所有量化等级为u的像素点对应的核函数的和与所有像素点对应的核函数的和的比值。为便于硬件实现，将其分解为两步进行：第一步，核函数统计算法核包括近似后的核函数k（x）、各量化值对应的核函数和qsumu和所有核函数的和第二步，直方图归一化（即将qsumu归一化），得到核函数加权的直方图。第一步计算过程经核函数变化后只涉及加法运算，第二步计算过程涉及整数的除法运算。

2.3 偏移矢量的优化

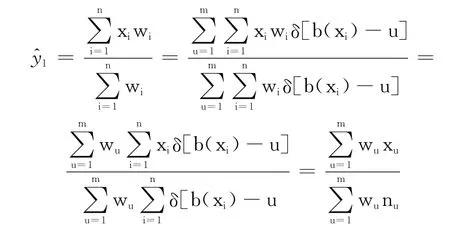
由上面的分析可以看出，偏移矢量的计算可以分两步进行：第一步坐标偏移统计核，负责计算xu、nu，只涉及加法运算；第二步坐标偏移和加权，利用权重系数加权，求得偏移矢量，涉及浮点乘、除运算。与原算法相比，此过程为全等运算，只是改变了运算规则，并没有进行近似。

2.4 尺度更新

Mean Shift算法在跟踪过程中无窗口更新机制，对尺度变化目标的跟踪效果不好。为了适应尺度变化目标的跟踪及算法实时性，采用参考文献[7]中连通域标记方法提取目标面积，按照参考文献[8]中所述的方法进行尺度更新。

3 系统的硬件结构及软件实现

3.1 系统的硬件结构及软硬件划分

设计采用下面的嵌入式平台实现Mean Shift算法，其硬件结构框图如图2所示。

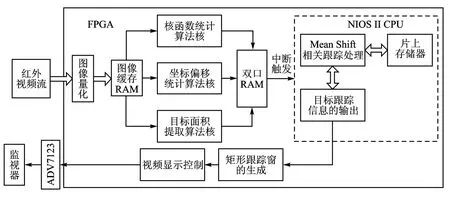
图2 嵌入式系统的硬件结构框图

由硬件结构框图可以看出，整个算法基于单片FPGA，利用SOPC技术实现，并将跟踪结果经ADV7213 D/A转换后输出给监视器。利用硬件编程实现核函数统计算法核、坐标偏移统计核和目标面积提取算法核；利用软件编程实现Mean Shift的相关处理，包括直方图归一化、坐标偏移和加权、偏移权重和迭代判决。硬件部分采用硬件编程语言VHDL并行流水实现，并将计算结果写入双端口RAM中，触发CPU进行软件操作。软件操作流程图略——编者注。首先，CPU从双端口RAM中读取FPGA的计算结果，计算目标模型或候选模型；其次，CPU计算各量化值对应的权重，同时从双端口RAM中读取FPGA统计的各量化值计算结果，求得目标新的中心位置；最后，CPU计算迭代是否满足终止条件，若满足条件，则将计算结果输出到监视器上，并读取面积结果更新跟踪窗的尺度，若不满足，则将新位置通知FPGA，由FPGA重新统计目标区域的特征并送入CPU重新计算。

3.2 软件优化

在介绍软件优化前，先介绍一下本设计选用的CPU的基本配置。CPU选用快速的NIOS II/f型处理器，具有6级流水结构，带指令和数据缓存；CPU主时钟采用100 MHz；CPU开辟的数据与指令Cache均为32 KB；构建哈佛结构的处理器，程序存储器和数据存储器分开，程序存储器和数据存储器均采用片上RAM实现，大小为64 KB。

（1）NIOS II软件配置的优化[9]

减少代码量：使用裁减后的小封装驱动库，勾选库属性中的reduce device drivers选项；使用基本的C语言库，勾选库属性small C library选项。经勾选后，软件代码由76 KB减少到23 KB。

（2）自定义浮点指令[10]的应用

自定义指令是指将复杂的运算或需要很多时钟周期才能完成的运算采用独立的硬件来实现，将这些硬件按一定的接口时序封装集成到CPU中。系统生成时，将为每条用户指令产生一个宏，可以在应用程序中调用这个宏代替原来软件实现部分，使系统的运算能力大大提升。由前面的分析可以看出，Mean Shift运算过程中用到大量的浮点加、减、乘、除和开平方运算，在CPU的Custom Instructions里添加Floating Point Hardware并勾选硬件除法器选项，CPU在实现时自动将浮点加、减、乘、除运算用自定义指令实现。自己编写浮点开方指令altfp＿sqrt＿top，并添加到Custom Instructions选项中，CPU调用其对应的宏实现浮点开平方运算。各自定义指令的硬件加速情况如表2所列。

4 试验与分析

系统硬件平台的核心为FPGA，选取Altera公司的FP2S180F1020I4，实验中采用的红外视频图像分辨率为352×288。

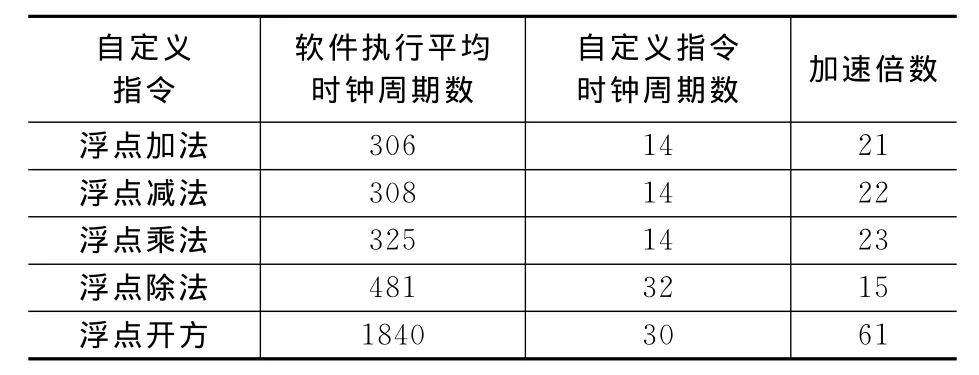
表2 浮点自定义指令的硬件加速比

4.1 尺度变化目标实验

实验以天空中的飞机视频序列为测试对象，测试算法对目标尺度变化、旋转状态下的跟踪能力。跟踪序列在第15帧、115帧和215帧的跟踪图像略——编者注。在目标发生较大尺度变化和旋转时仍能准确的跟踪目标。

分别应用本文提出的两条优化措施对算法进行优化加速，其优化效果如表3所列。

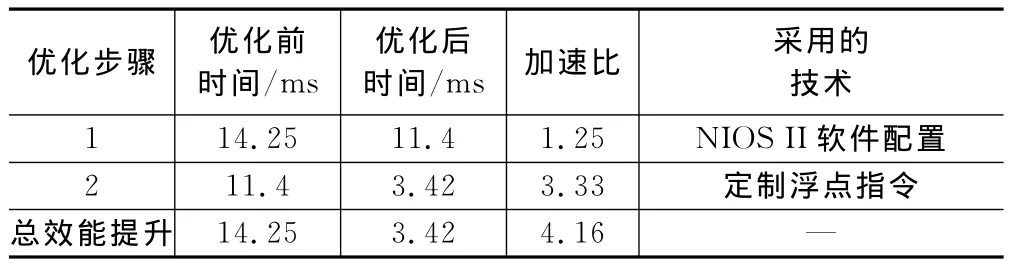
表3 算法的优化效果

跟踪飞机视频序列的处理时间如图3所示，实验中，目标尺度从15×10逐渐增大到90×60，其平均计算时间为3.42 ms，最大处理时间小于4 ms，可满足对大部分红外视频序列的实时跟踪。

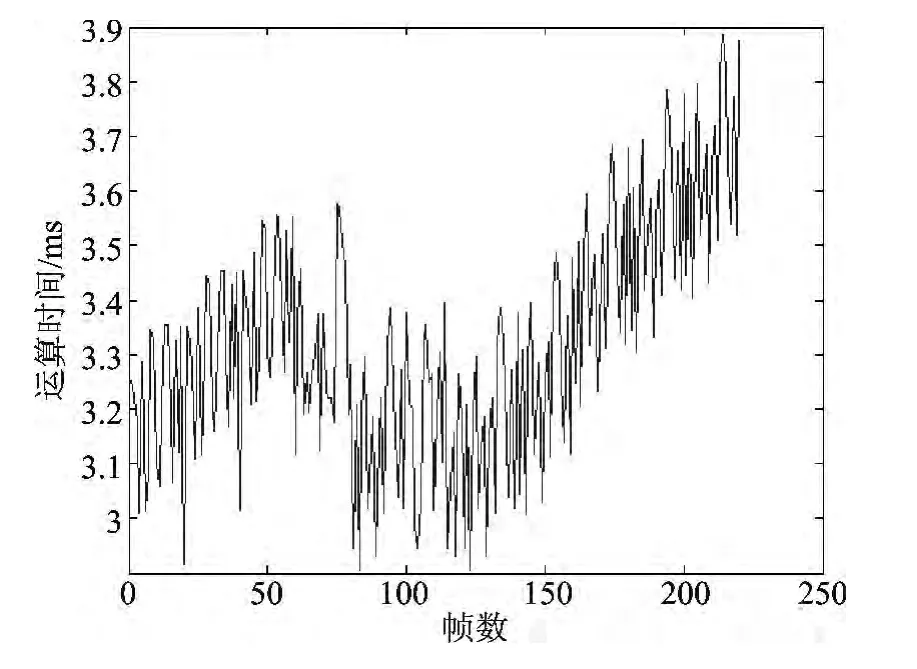
图3 嵌入式系统的处理时间

4.2 算法处理时间对比

应用本文提出的方法和参考文献[5]中采用FPGA＋DSP实现方法对比，可以看出，参考文献[5]中改进的方法随着目标尺度变化，处理时间迅速增加；而本文方法处理的跟踪时间，受目标尺度变化的影响很小。这是因为通过软硬件划分后，软件的处理时间不受目标尺度的影响，硬件处理时间与目标尺度成线性关系，但因为采用流水并行实现，所以处理时间的增加很少。算法的不同实现方式处理时间的对比如表4所列。

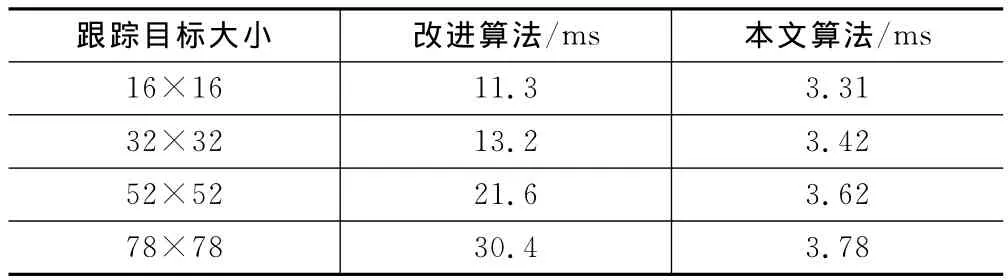
表4 算法的不同实现方式处理时间的对比

结 语

本文利用SOPC原理对均值漂移算法进行软硬件划分，降低了算法实现的复杂度，使其适合在FPGA上实现；又结合FPGA的硬件特点，提出了实时整数运算核，并行流水提取相应的目标信息；最后，结合NIOS II CPU的特点，对软件实现部分进行优化，提高算法的执行效率。实验结果表明，该系统实时性强，能在4 ms内完成对目标的跟踪，对目标的尺度变化具有自适应性。

编者注：本文为期刊缩略版，全文见本刊网站www.mesnet.com.cn。

参考文献

[1]Comaniciu D，Ramesh V，Meer P.Kernel-based object tracking[J].IEEE Trans.on Pattern Analysis and Machine Intelligence，2003，25（5）：564-577.

[2]Anbang Yao，Guijin Wang，Xinggang Lin，et al.An incremental Bhattacharyya dissimilarity measure for particle filtering[J].Pattern Recognition，2010，43（4）：1244-1256.

[3]R Venkatesh Babu，S Suresh，Anamitra Makur.Online adaptive radial basis function networks for robust object tracking[J].Computer Vision and Image Understanding，2010（3）：297-310.

[4]Leichter Ido，Lindenbaum Michael，Rivlin Ehud.Mean Shift tracking with multiple reference color histograms[J].Computer Vision and Image Understanding，2010（3）：400-408.

[5]孙航，韩红霞，郭劲，等.基于均值偏移快速算法的红外目标跟踪[J].仪器仪表学报，2012，33（5）：1122-1127.

[6]Comaniciu D.Nonparametric robust methods for computer vision[D].New Jersey：The State University of New Jersey，2000.

[7]Liu Qing，Tang Linbo，Zhao Baojun，et al.A fast target tracking algorithm basted on connected component labeling and grey value statistics[C]//ICCASM，2012：1267-1270.

[8]刘晴，唐林波，赵保军.跟踪窗自适应的Mean Shift目标跟踪算法[J].系统工程与电子技术，2012，34（2）：409-412.

[9]叶有时，赵保军，唐林波，等.多目标实时跟踪可编程片上系统的软件优化[J].光学精密工程，2011，19（3）：681-689.

[10]Altera.Embedded Design Handbook，2010.