从量子力学层面上认识，到大学物理层面上理解顺磁性和抗磁性

周雨青

（东南大学物理系，江苏 南京 211189）

国内主流大学物理学教材[1-3]都是这样来描述顺磁质和抗磁质的：在固有的分子磁矩μm＝0的磁性介质中，分子中的每一个电子的运动都相当于一个圆电流，磁矩为μe.由于电子带负电，电子的角动量L与其磁矩μe方向相反.在外磁场B0中，电子磁矩受到磁力矩MB＝μe×B0的作用，磁矩μe（角动量L）将绕外磁场B0作进动，该进动又相当于一个圆电流，将产生一个附加磁矩Δμe.无论电子运动方向如何，Δμe的方向都与外磁场B0方向相反，即产生了抗磁性的抗磁质；在固有的分子磁矩μm≠0的磁性介质放入外磁场B0中后，分子磁矩μm所受的磁力矩将使其方向转向（倾倒）与沿外磁场方向一致，即产生了顺磁性的顺磁质.

问题是，同样的磁矩，一个是原子层面上的电子磁矩μe，另一个是分子层面上的磁矩μm，都在外磁场B0中，为什么前者是“进动”，后者却是“倾倒”呢？显然，机理描述上不自洽.实际上，原子或分子（以下统称原子）在磁场中表现出的行为——顺磁性、抗磁性、铁磁性，甚至反铁磁性等都是由原子与外磁场的量子作用表现出来的，体现在量子力学的哈密顿量中.以下只研究弱磁性物质的顺磁与抗磁问题.

1 顺磁、抗磁在量子力学中的描述

1.1 原子在外磁场中的哈密顿量

以下用磁场强度H作为参变量写出哈密顿量.因外加磁场在原子范围内可看做均匀磁场，所以考虑多电子原子在均匀磁场H中的哈密顿量为

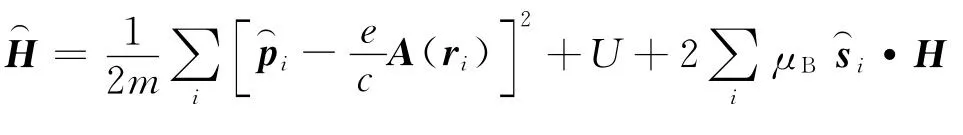
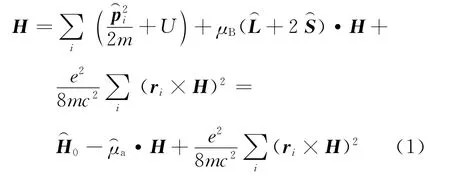
其中第一项为没有磁场时的原子哈密顿量，它决定了原子主能级，又称本征能量可以看作原子的“固有”磁矩算符，没有外磁场时仍存在，因此第二项是原子磁矩在外磁场方向上的投影引起的简并能量的分离——塞曼能级，后面将会看到这一项就是顺磁效应的主要贡献项；第三项与原子的内禀性质无关，纯粹是外磁场的存在对电子位置的“诱导”而产生的，后面将会说明它决定了抗磁性.

1.2 磁性的确定

根据统计物理规律，N个原子（或离子）组成的系统的磁化率χ可以通过下面几个关系获得

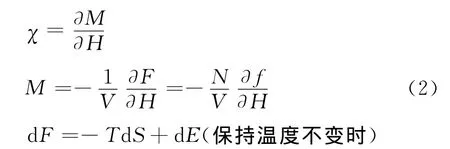
其中，M为磁化强度；f为单个原子自由能，在近独立子模型中F＝Nf；V、T分别为系统体积和温度；S为熵；E为系统的内能.根据量子统计基本原理，由N个近独立原子（粒子）组成的系统，在温度为T达到热平衡时，单个原子平均的自由能f与原子内能变化ΔEn由正则系统的配分函数Z联系在一起，即

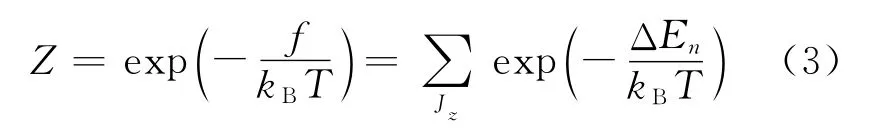
式中的Jz是确定内能变化的参变量，后面会看到是原子的总角动量量子数.原子的内能变化就取决于式（1）中的第二、三项在对应量子态中的能量.通过计算磁化率χ就可判断物质的磁性，χ＞0为顺磁，χ＜0为抗磁.由此可知，物质的磁性取决于原子在外磁场中的能级变化.

1.3 第n个量子态的原子能量改变

用标准的量子语言说，第n个量子态是指零级哈密顿量H0对应的 （L2，S2，J2，Jz）共同本征态，对应的量子数是（n，l，m，s）.为方便起见，本文用｜n〉记作第n个上述本征态.假设外磁场在z方向，即H＝Hz，根据微扰论，只求一级微扰的能级改变为

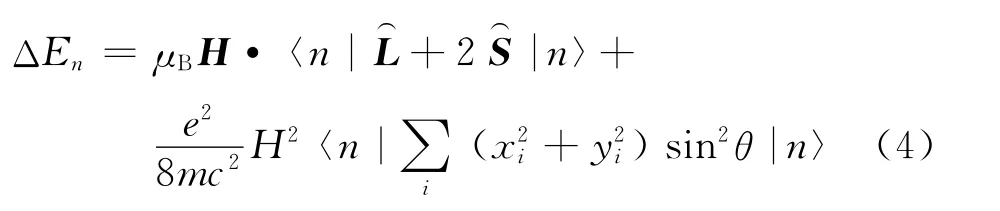
式（4）中的第一项的量级为μBH，当磁场强度为1T时，此项约为10-4eV；第二项的量级为其中aB为玻尔半径，当磁场强度为1T时，此项约为10-9eV.由此可以看出，当式（4）第一项不为零时，主要由第一项来决定原子能量改变，只有第一项等于零后，第二项才起作用，对应的磁性也是如此.

1.4 顺磁与抗磁的出现

（1）讨论式（4）中的第一项

根据原子及量子物理，原子固有磁矩可写成

其中，

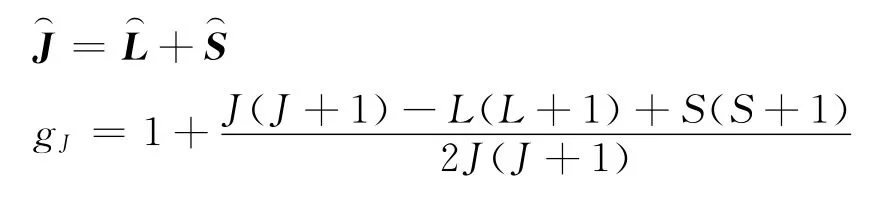
分别为原子的总角动量算符和原子的朗德因子.由此可以看出该项强烈依赖于电子壳层的排列.当原子（或离子）中的电子满壳层排列时，L＝S＝J＝0，原子没有固有磁矩，此项等于零.当电子未满壳层时，原子存在固有磁矩，此项不为零，下面我们来计算由这一项引起的磁化率.

取原子基态｜0〉，将式（5）代入式（4）中计算原子在磁场作用下的内能变化

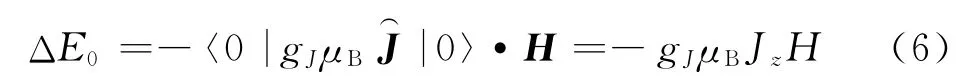
其中Jz＝-J，-J＋1，…，J-1，J.这表明，具有固定磁矩的原子（或离子）在外磁场中的内能变化有2J＋1个分立的值.同时表明，由于壳层未满，外磁场可以改变多电子系统中的电子分布，从而系统的熵会发生改变，因此系统的自由能变化并不等于内能变化，它们之间只能通过式（3）联系.将式（6）代入式（3）有

由式（2）可得N个近独立原子系统的磁化强度

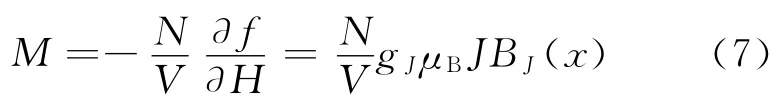
用Matlab程序画出全函数域内的布里渊函数BJ（x）-x图，如图1所示.其中J取3／2.在弱场近似下BJ（x）函数可展开为

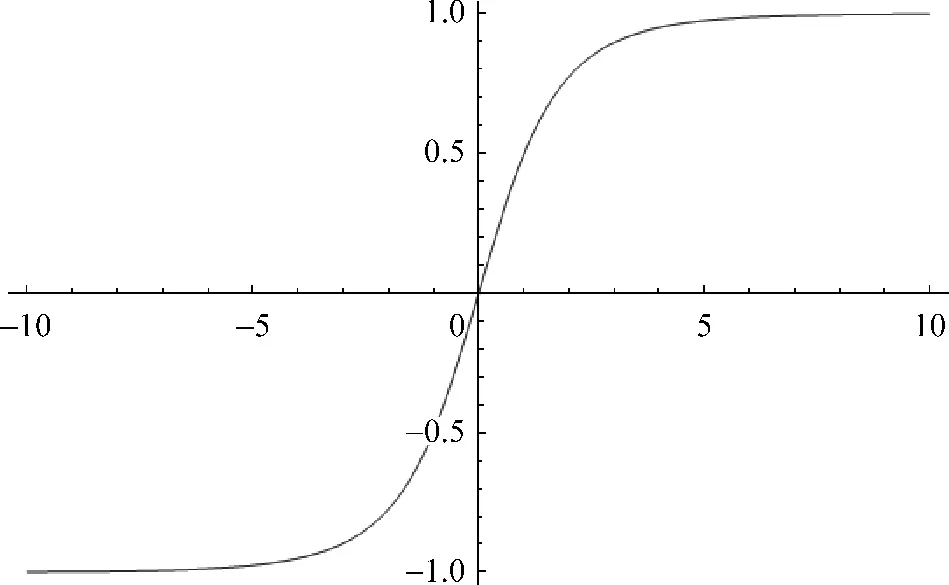
图1 BJ（x）-x图

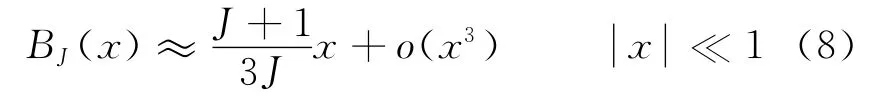
因此在弱磁场下，由式（2）、（7）、（8）可得

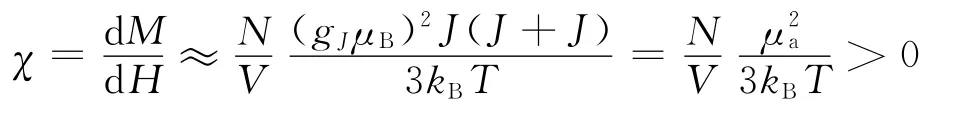
所以，当原子非满壳层时，原子在磁场中表现出顺磁特性，是由原子固有磁矩起主要作用.

（2）讨论式（4）中的第二项

首先，式（4）的第二项是从式（1）的第三项来的，从中可以看出，没有外磁场的存在，这一项是不存在的，这不同于固有磁矩，所以这一项可以说是磁场“诱导”出来的.其次，当L＝S＝0时状态波函数是球对称的，因此最后，计算这一项引起的磁化率.当L＝S＝J＝0时，原子在外磁场中的能量变化

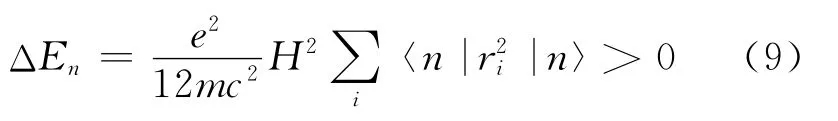
由于外磁场不能改变满壳层的多电子系统的电子分布，所以系统的熵不依赖外磁场，系统的自由能变化就等于内能的变化∂f＝∂ΔEn，因此将式（9）代入式（2）有

所以，固有磁矩等于零的原子（离子）系统，表现出抗磁，是由外磁场诱导生出的.由量子力学的分析知，无论是顺磁还是抗磁，都是由“相互作用能”的形式决定的.

借助调研统计结果，综合研究分析显示，油田博士后科研成果30%以上属于质量较高、价值较大、转化较多、应用效果较好的成果，但同时，调研数据也显示，仍有部分成果没有全部转化，或没有转化，或转化了效果不明显。

2 量子磁性的模型化理解

实际上，物质的磁性本身是一种量子力学效应，但可以有经典意义的“模型化”理解.比如，量子力学中虽然没有轨道概念，但却有表征自由度的角动量，也就有了对应经典概念的固有磁矩，也就有了式（1）中的第二项，从而就有了顺磁性；有磁矩，在磁场中就应该有拉莫尔进动，进动诱导出的磁矩对能级的影响在哪儿呢？考察式（1）的第三项对应的式（9），其中的是电子分布位置自由度的平方平均值，对应了经典概念的电子轨道半径的平方，没有磁场时也应该存在，但不会有磁矩，一旦加了外磁场，由于拉莫尔进动的存在，诱导出了磁矩（电流乘以面积元）μind，该磁矩引起的能级变化就是式（1）的第三项，即式（9），且可以写成

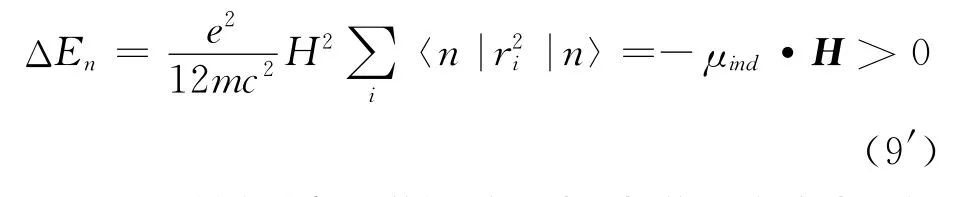
即原子系统的诱导磁矩总是与外磁场方向相反，即为抗磁性，这与量子力学计算是一致的.由上可见，量子力学对顺磁和抗磁的“模型化”描述都是从磁矩在磁场中的附加能出发研究磁化问题，方法是自洽的.

可是目前国内大学物理层面上的许多教材，对此的描述却难以自圆其说，甚至与经典物理中的基本概念冲突.

3 大学物理教材上有关顺磁性和抗磁性描述的不恰当之处

3.1 顺磁性与抗磁性描述的不自洽之处[1-3]

文献[1]、[2]、[3]，甚至国内大学物理所有教材，对顺磁性的解释一律表述为：在外磁场作用下，原子（或分子）固有磁矩所受到的力矩使分子的固有磁矩方向转向（倾倒）与外磁场方向一致.…….而对抗磁性的解释，文献[2]、[3]，或大多数教材，以电子轨道磁矩的旋进来解释原子（或分子）抗磁的产生.这就出现了同样是磁矩，一个是“倒向”，一个是“旋进”的不自洽说法.

3.2 抗磁性的3种经典描述不统一和存在问的题

抗磁性在国内大学物理教材上通常有3种机理的解释.

（1）电子轨道的旋进机理[2，3]

拉莫尔进动诱导出的磁矩解释法.这就是上述量子力学计算中的模型化，这种解释是与量子力学的认识相容的.

（2）电子轨道的洛伦兹力机理[1，4]

（3）电子轨道的磁感应机理[2]

文献[2]P330还给出一种感应环流效应解释抗磁性，认为施加磁场的瞬间会感应出环流电场，从而推动电子运动形成环流磁矩.这种解释似乎还能阐明洛伦兹力机理中的电子加速问题.但是，环流电场会因磁场的稳定而消失，环流在没有持续推动力作用下会随着热平衡的建立消耗在电阻之上，从而稳定的抗磁性不复存在.

显然，第一种机理描述是最恰当的.

4 回避问题的建议

因大学物理的局限性，不可能也没必要在大学物理层面上对顺磁性和抗磁性做量子力学的陈述，但又不能出现明显的不自洽描述.

正如上述量子力学陈述，顺磁性不能理解成在磁力矩作用下的“倾倒”，它只是因外磁场的出现使原子有了附加能量式（6），不同角动量的附加能不同，由于热平衡的作用，原子倾向于按玻尔兹曼分布，取能量最低分布最多的状态，这等价于原子固有磁矩取与外磁场方向一致的状态最多，就形成了顺磁性.因此，在大学物理层面上解释顺磁性，我们建议按文献[6]P800的说法：……，（当顺磁物质）置于外磁场中，磁偶极矩倾向于沿磁场方向排列，…….这种说法既避免了磁力矩作用下的“倾倒”机理，又与量子概念保持了实质上的一致.从而避免了与抗磁“旋进”解释的明显不自洽性之处.

5 几点说明

（1）为什么本文只对原子，而不是分子进行分析？

首先，分子只是多个原子的组合；其次，分子磁矩与多电子原子的磁矩区别在于，前者多出核-核之间的角动量磁矩，但该磁矩很小，一般忽略，因此，分子与多电子原子的磁矩基本等效.

（2）-μa·H的二级微扰项为何不考虑？

在处理微扰能级分裂时，式（1）中的第二项-μa·H的二级微扰项的数量级实际上比式（1）的第三项的一级微扰项要大，但由于它比该项的一级微扰大约小3个数量级，且可以证明[5]这个二级微扰项在基态原子态中对磁矩的贡献是顺磁的，因此在计算顺磁作用时，不影响对第二项的一级微扰的磁性判断，却少了许多计算上的麻烦.同时，这一项在原子满壳（J＝L＝S）时也为零，所以不影响第三项的抗磁判断.

（3）顺磁质中顺磁性和抗磁性都有

量子力学中算顺磁率时，虽然只考虑了式（4）的第一项，但实际上第二项（抗磁效应）是参与到原子内能变化中的，按理说是应该加入到通过式（3）计算的自由能中去，从而计算出磁化率的，但因为该项比第一项小很多，不会影响计算出的顺磁结果.

（4）小磁针为什么在磁场中顺着磁场方向“倾倒”？

本文实际上是在谈磁化的机理，物质在被磁化以前，组成物质的原子或分子，无论固有磁矩是否为零，都像一个高速旋转着的陀螺.一旦物质被磁化，所有磁化机理过程都结束，物质就像一个静止的陀螺，所以小磁针只会沿着磁场方向倾倒（如果此时再说小磁针要旋进，那就相当于二次磁化了）.

6 结语

顺磁性的“倾倒”概念在教材中、老师头脑中可能已经根深蒂固了.大学物理虽然需要模型化、形象化和简易化，但不能丧失科学化，原子或分子在具有角动量情况下拥有的磁矩，绝不可能向着磁场方向倾倒，这是基本的力学常识.顺磁是统计分布的结果，不是力学结果，这个结论应该在大学物理教材中得到确认.

审稿意见摘录：

本文中所用的方程以及对物质产生顺磁性和抗磁性的物理机理的分析是正确的.文章对大学物理如何讲述相关问题提出了有益的建议.因此，审稿人建议发表此文.

文章中有一些对流行的大学物理教材某些段落的评判，审稿人认为：这些只是不同的说法，并非物理内容的“正”、“误”之争.作者可以这样写，但若读者提出不同的意见也是正常的.

[1]马文蔚.物理学[M].5版.北京：高等教育出版社，2006：277-278.

[2]张三慧.大学物理学 第三册[M].电磁学2版.北京：清华大学出版社，1999：290-292.

[3]陆果.基础物理学 上卷[M].北京：高等教育出版社1997：351-352.

[4]胡友秋.电磁学[M].北京：高等教育出版社，1994：249.

[5]朗道.量子力学 下册[M].北京：高等教育出版社，1981：201.

[6]哈立德.物理学基础（原书第6版）[M].张三慧，等，译.北京：机械工业出版社，2005.

[7]黄昆.固体物理学[M].北京：高等教育出版社，1988.

[8]Ashcraft N W，Mermin M D.Solid state physics[M].New York：Holt，Rinehart and Winslon.1976.