某小口径弹丸外流场空气动力特性仿真

王洪超，王雨时，闻泉

(南京理工大学 机械工程学院，江苏 南京 210094)

某小口径弹丸外流场空气动力特性仿真

王洪超，王雨时，闻泉

(南京理工大学 机械工程学院，江苏 南京 210094)

为了给某小口径杀伤破甲弹引信设计提供参考，运用GAMBIT建立弹丸外流场数值仿真模型，通过FLUENT对弹丸外流场进行了数值仿真以获取相关的气动力规律。仿真结果与1943年阻力定律基本一致，计算所得的气动参数可以为小口径杀伤破甲弹引信的外形设计提供依据与参考。

弹丸； 外流场； 气动力特性

0 引言

弹丸外形决定了其空气动力特性和作战效能[1]。传统气动力外形设计方法在对不同设计方案进行风洞试验综合分析的前提下得到最优的设计方案[2]。该方法设计周期长、效费比低的缺点已不能适应现代武器设计的要求。数值仿真在一定程度上可以代替风洞试验，并且可以模拟风洞试验无法模拟的条件，提供多种计算模型可用于模拟不可压或可压流动、定常状态或者过渡分析、无黏、层流和湍流等情况，具有极强的流场仿真分析能力，可用于进行气动力设计及气动特性参数计算[3]。

文中采用FLUENT对某弹丸进行外流场数值仿真，得到阻力系数、升力系数随马赫数、攻角的变化规律。仿真结果与1943年阻力定律相符，计算所得的气动参数可以为小口径杀伤破甲弹的外形设计提供依据与参考。

1 数值模型

1.1 弹丸有限元模型

某小口径杀伤破甲弹简化为如图1所示几何模型。由于研究的是弹丸外流场，所以建立直径和长度均是弹丸直径和长度20倍的圆柱体来模拟弹丸外部流场，避免边界反射引起空气流场中的压力计算不稳定。弹丸置于空气流场计算域中心位置，假设弹丸表面为绝热壁，弹丸附近网格加密以准确获得阻力系数和升力系数。

图1 某小口径杀伤破甲弹几何模型

1.2 初始条件与边界条件

文中所研究的马赫数和攻角情况都属于定常流动范围，采用相对运动条件模拟弹丸附近的外流场，即假设弹丸静止，假设来流为理想气体，选择萨兰德定律计算气体粘性，空气以反向相同速度流动，计算域边界条件设置为远场压力条件，湍流模型采用S-A(spalart-allmaras)模型[4]。由于求解的是可压缩流体，涉及总压和静压等多种压力，所以为便于设置边界条件和计算结果的后处理，将参考压力置为零[5]。

1.3 气动特性求解

弹丸的阻力与产生阻力的面积、飞行速度、飞行高度和迎角有关，为了说明阻力特性，用单位面积和单位动压条件下产生的压力，即阻力系数表示[6]：

式中：X为阻力，ρ为空气密度，v为气流相对于弹丸的流速，S为参考面积。

与阻力系数相似，升力系数Cy与升力Y之间的关系可表示为：

式中：Y为升力；ρ为空气密度；v为气流相对于弹丸的流速；S为参考面积。

2 仿真结果

计算弹丸在来流马赫数分别为：M=0.20、0.40、0.60、0.80、0.85、0.90和0.95，攻角分别为α=0°、2°、4°、6°、8°、10°、12°、14°、16°时的空气流场。某小口径杀伤破甲弹气动力参数仿真结果如表1所列。表中Cx为阻力系数，Cy为升力系数。参考长度为弹丸长度，以弹丸最大横截面积为参考面积。

2.1 阻力特性

根据表1得到的阻力系数随马赫数变化规律如图1所示，马赫数<0.8时，阻力系数比较平稳；马赫数>0.8，阻力系数随马赫数增大而明显增大；在一同马赫数下阻力系数随α增大而增大。

根据表1得到的阻力系数随攻角变化规律如图2所示，当马赫数<0.8时，阻力系数随着攻角的增大而增大，其变化规律近似呈线性规律；不同马赫数下阻力系数随攻角的变化曲线变化很小。当马赫数>0.80时，阻力系数随攻角的增大而增大，其变化规律近似于抛物线。

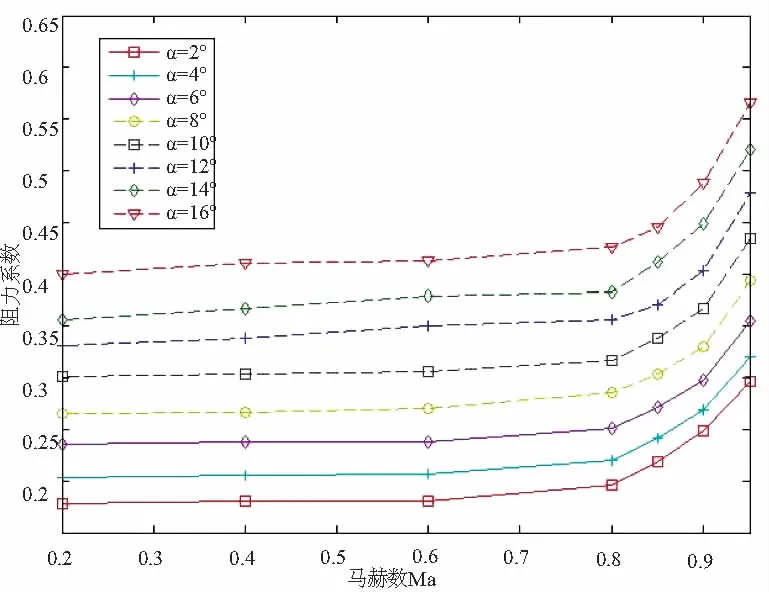
图1 阻力系数随攻角变化曲线

图2 阻力系数随攻角变化曲线

Ma气动系数攻角(°)02468101214160．20Cx0．16530．17810．20340．23600．26560．30100．33080．35660．3994Cy0．00000．02840．06370．12070．16420．20760．23180．29320．32080．40Cx0．16760．18060．20540．23740．26620．30380．33880．36660．4100Cy0．00000．02920．07360．12370．16930．21300．23380．30260．32180．60Cx0．16910．18100．20700．23800．27080．30580．34980．37880．4130Cy0．00040．03120．07420．12390．16970．21580．24060．30640．33440．80Cx0．18970．19650．21980．25160．28600．31740．35680．38280．4262Cy0．00060．03380．07610．12530．17020．21680．25080．30800．34680．85Cx0．21420．21880．24100．27160．30360．33820．37020．41140．4446Cy0．00100．03450．07730．12840．17800．21740．25700．31000．34880．90Cx0．24720．24920．26900．29820．33020．36700．40240．44860．4882Cy0．00160．03560．07880．13700．18130．22420．26620．31580．36540．95Cx0．29000．29620．32060．35480．39300．43440．47800．52020．5662Cy0．00220．04020．08990．14610．20420．26120．31660．37440．4268

2.2 升力特性

根据表1得到的升力系数随马赫数变化规律如图3所示，攻角<4°时，升力系数随马赫数增大基本上变化不大；当攻角>4°、马赫数<0.80时，升力系数随马赫数的增大而缓慢增大，当马赫数由0.9增大至1时，升力系数随马赫数增大而迅速增大。

图3 升力系数随马赫数变化曲线

根据表1得到的升力系数随攻角变化规律如图4所示，在不同的马赫数下，升力系数都是随攻角的增大而增大的，可近似为线性关系；当马赫数<0.9时，升力系数随马赫数变化曲线差别不大；当马赫数>0.9时，升力系数随马赫数的增大而明显增大。

3 仿真结果验证

查阅文献[7]，得到来流马赫数0.85的1943年标准阻力函数Cx0(0.85)为0.166，来流马赫数0.9的标准阻力函数Cx0(0.9)=0.184，来流马赫数0.95的标准阻力函数

4 结语

运用FLUENT软件对弹丸外流场进行数值仿真，利用仿真结果分析阻力系数、升力系数随马赫数、攻角的变化规律，仿真结果与根据1943年空气阻力定律得到的结果吻合较好，可以为方案设计提供依据。

[1] 韩子鹏. 弹箭外弹道学[M]. 北京：北京理工大学出版社，2008.

[2] 王保国，刘淑艳，黄伟光. 气体动力学[M]. 北京：北京理工大学出版社，2005.

[3] 苗瑞生，居贤铭，吴甲生. 导弹空气动力学[M]. 北京：国防工业出版社，2006.

[4] 郑健，周长省，鞠玉涛,等. Spalart-Allmaras湍流模型在弧形翼超音速流场数值模拟中的应用[J]. 重庆工学院学报，2008，22(12)：34-39.

[5] 于勇. FLUENT入门与进阶教程[M]. 北京: 北京理工大学出版社，2008.

[6] 赵育善，吴斌. 导弹引论[M]. 西安：西北工业大学出版社，2009.

[7] 徐明友. 火箭外弹道学[M]. 北京：兵器工业出版社，1989.

Flow field Aerodynamic Characteristics Simulation of Small Caliber Projectile

WANG Hongchao, WANG Yushi, WEN Quan

(School of Mechanical Engineering, Nanjing University of Science & Technology, Nanjing 210094, China)

In order to provide a reference for design of the small-caliber high explosive ammunition fuze, projectile flow field numerical simulation model is established by GAMBIT and the projectile flow field is simulated by FLUENT to obtain the relevant law of aerodynamic force. The simulation results agree with 43 basic law of resistance, calculated aerodynamic parameters provide basis and reference for the design of the appearance of the small-caliber high explosive ammunition fuze.

projectile; flow field; aerodynamic characteristics

王洪超(1988-)，男，河北廊坊人，硕士，从事小口径弹药引信外形设计及其气动特性研究。

TJ 012; TP391.9

B

1671-5276(2015)05-0099-03

2014-01-13