四杆机构的疲劳分析及优化

闫思江，韩晓玲，孙玉新，孙莉莉

（青岛港湾职业技术学院 机械系，山东 青岛266404）

0 引言

强度、刚度和疲劳寿命是对工程结构和机械使用的三个基本要求。疲劳是结构失效的最主要的原因。引起疲劳失效的循环载荷往往小于根据静强度分析的“安全”载荷，传统的静强度分析方法不能解决疲劳问题。

据统计，50%～90%的结构失效源于结构疲劳问题[1]。结构疲劳设计需要密切联系疲劳物理现象并揭示结构在实际工作过程中的裂缝形式，因此需要一个有效的疲劳设计分析工具。如何利用现代技术解决工程实际中的疲劳问题，是目前迫切需要解决的问题，本文依托HyperWork 平台通过实例给出了完整的疲劳分析方法和步骤。

1 疲劳分析的基本流程

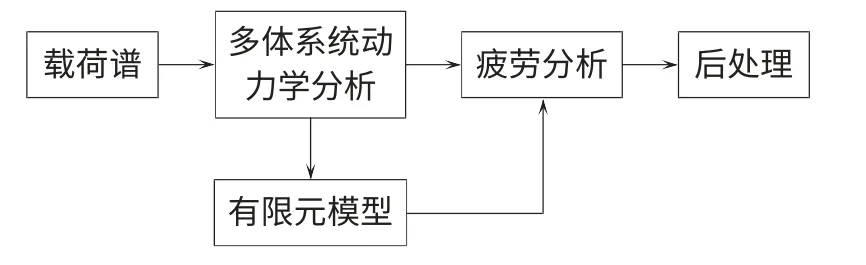
图1 疲劳分析流程

当同时存在多个载荷工况而且每个工况都独立时，可以使用线性叠加原理将各工况组合到一起，然后再确定组合工况下各计算点的应力值。工况组合方程如下：

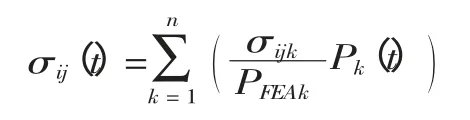
式中：n——工况数量；

Pk（t）、σij（t）——分别表示第k 个载荷时间历程变量和总应力张量；

PFEAk、σijk——分别表示第k 个载荷的大小和应力张量。

载荷谱一般要通过实际测试得到，现在随着计算机的发展，使通过仿真计算获取载荷谱成为可能。本文采用HyperWorks 中的MotionSolve 获取。

2 多体动力学仿真

在MotionView & MotionSolve 环境中，以四杆机构为例，对其进行动力学仿真。其运动简图如图2所示。

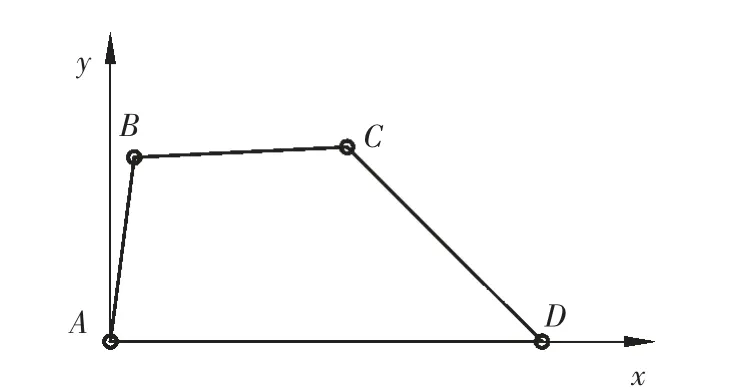
图2 四杆机构简图

2.1 创建几何点、体

四杆机构由四个几何体组成，杆AB、BC、CD、DA，在默认情况下，MotionView 将自动创建DA 取名ground。一般情况下，这里需要输入另外三个构件相应的质量和惯性矩。然而建立仿真模型须将图2所示四杆机构模型中的A、B、C、D 四点坐标值及三个杆的重心位置坐标值输入。由于四杆机构各个坐标点不易确定，加上重心位置及大小、惯性矩大小人工不容易准确计算等原因，需采用其他方法间接获得。这里采用Pro/E 创建各个杆实体，然后装配，再导入运动仿真前处理软件MotionView 中，Motion－View 自动将坐标值、重心位置及大小、惯性矩大小等信息计算出来，省去了繁琐复杂的计算。

2.2 创建约束副

导入好几何体后，在各个回转点添加Revolutejiont 类型的铰链，其中Connectivity 面板中的body1和body2 分别选择相应的构件，旋转方向选择z 轴。

2.3 创建标记点

在回转轴处创建作用力与反作用力标记点I、J，以便输出载荷。

2.4 创建图形文件

几何图形可以来自隐式图形、基本图形或外部图形。在Connectivity 标签中关联到相应的实体重心处。本例采用来自Pro/E 的外部图形。其优点是准确、逼真。

2.5 定义驱动

将主动件（曲柄）处的Revelute jiont 采用表达式驱动如：10time。

2.6 定义输出

使用力函数FX（I,J,K）定义输出，该函数返回I，J 标记点之间的作用力。建好的模型如图3 所示。在曲线输出时，采用CSV 格式以便后面使用。

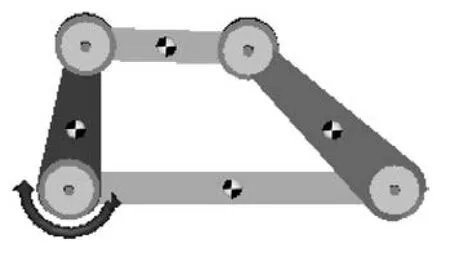
图3 运动仿真模型

2.7 提交MotionSolve运行

输出载荷谱（载荷时间历程）如图4、5所示。

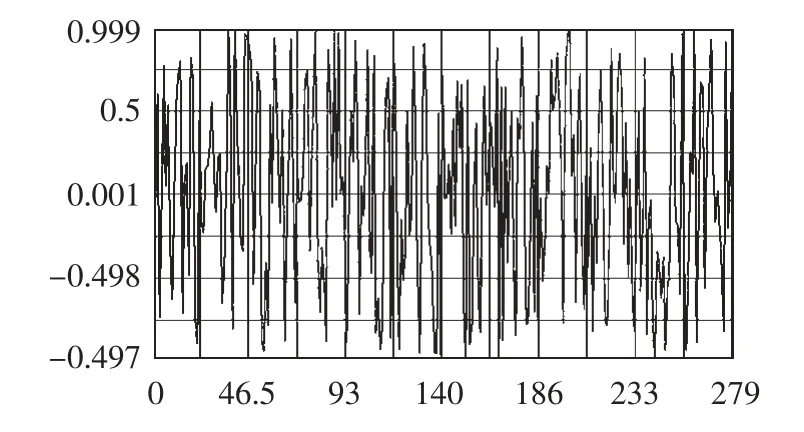
图4 水平方向载荷时间历程

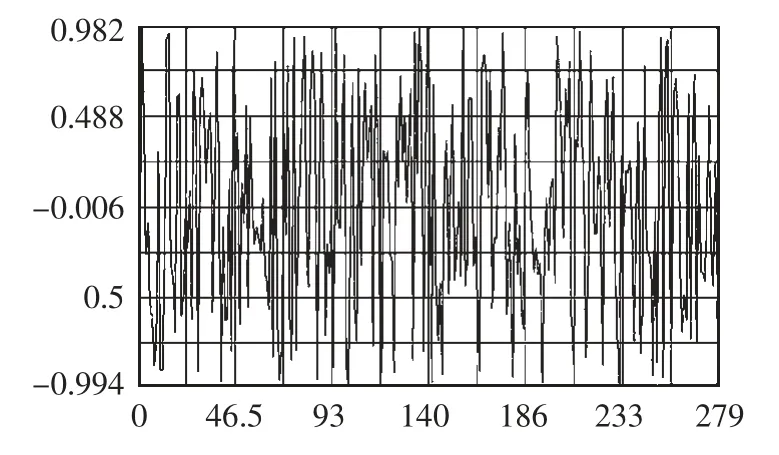
图5 垂直方向载荷时间历程

3 疲劳特性优化

3.1 启动疲劳流程树Process Manager

3.2 导入模型

导入的模型（由HyperMesh 完成）如图6 所示，这个模型中定义了两个静态工况、单元集、材料和属性等。

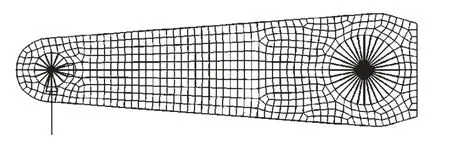
图6 连杆优化模型

3.3 创建疲劳工况

接下来的流程（分析参数、疲劳单元、属性和载荷历程等）均为该工况而定义。

3.4 定义疲劳分析参数和载荷时间历程曲线

平均应力修正方式，采用GOODMAN 方法，对于该方法而言，如果材料受到的拉伸平均应力大于材料的拉伸强度极限，那么就认为疲劳损伤程度大于1.0。加载由多体动力学仿真所获得的载荷时间历程即载荷谱图4、5 所示。

3.5 定义加载顺序

在这一步中，将创建一个包含两个载荷历程的事件。也就是说，要求在整个分析中两个载荷历程作用下的应力是线性的。使用这一事件，建立一个加载顺序。其中包括由动力学仿真获得的载荷谱图4、5。这里采用S_N(应力_寿命)方法。应力_寿命方法可以很好地计算结构在受到弹性变形范围内的循环载荷作用下的疲劳寿命。在这种载荷作用下，通常结构可以承受较多周期的作用，疲劳寿命较长，即高周疲劳。钢的S_N 曲线如图7 所示。

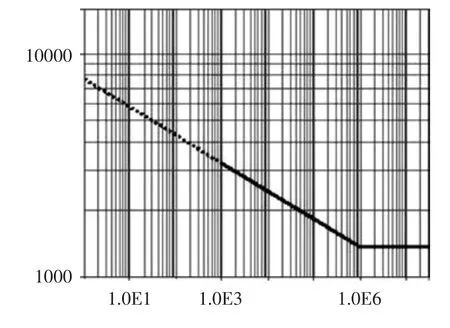
图7 实验得到的钢的S_N 曲线

S_N 方法是基于使材料发生弹性变形范围内周期载荷作用建立起来的，因此应使用S_N 曲线的寿命轴的数值大于1000 个周期部分以确保材料不发生明显的塑性变形。

3.6 创建自由形状设计变量

选中两个边界确定允许移动的距离，即优化空间。该步最好采用Hypermorph 手工进行。

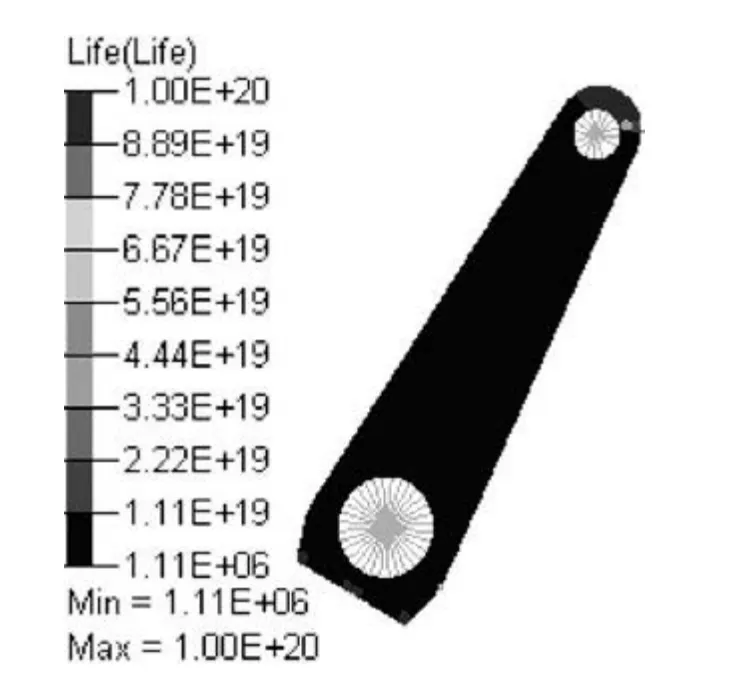
图8 第0 个迭代步的疲劳寿命云图

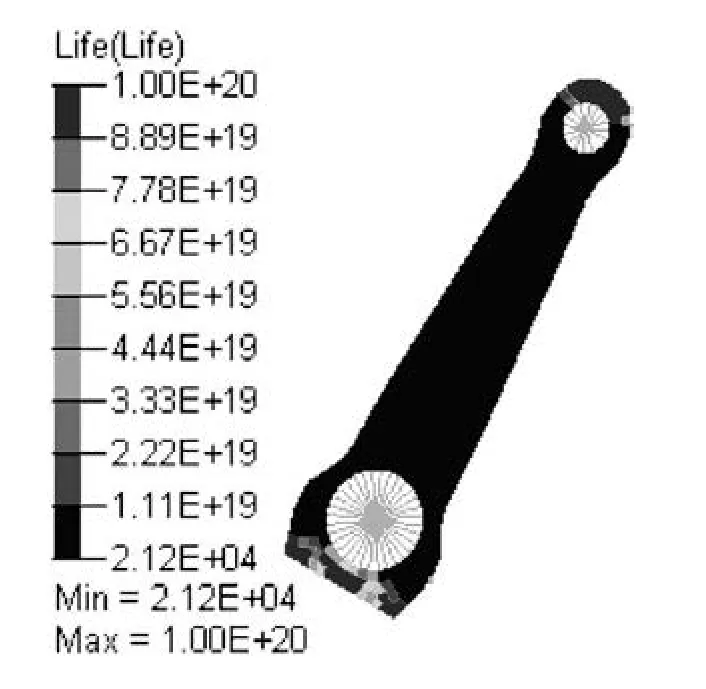
图9 第9 个迭代步的疲劳寿命云图

3.7 定义优化响应、约束、目标函数

将体积（质量）和寿命作为响应。约束优化条件设置为最低使用次数，如本例2.00e+04 次。在满足约束的情况下将体积最小化作为优化目标。

3.8 提交疲劳优化作业

4 观察结果

第0 个迭代步的疲劳寿命云图，体积4.67+02，最小寿命=1.11e+06。第9 个迭代步的疲劳寿命云图，体积=3.937e+02，最小寿命2.12e+04。表明在寿命不低于2.00e+04 的约束下，体积可降低至原来的3.93/4.67=0.84。图10 所示为曲柄优化后的形状云图。

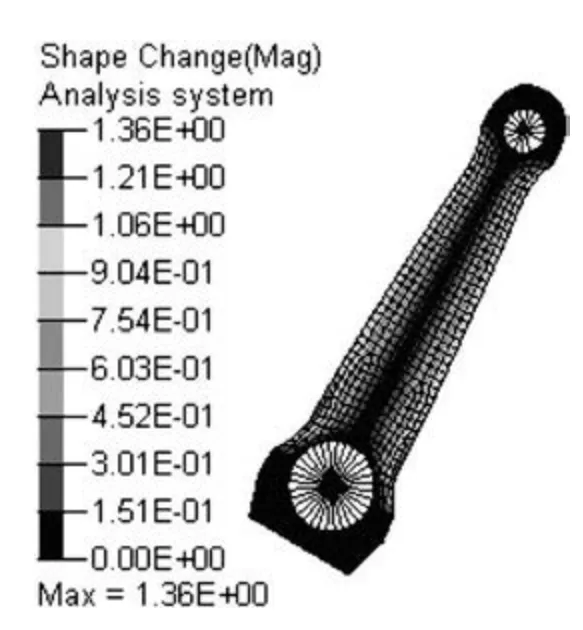
图10 形状变化云图

5 结束语

（1）虽然通过可靠的软件获得了载荷谱，但仿真方法需经试验验证才可确信。这里只是为试验提供参考数据。

（2）应用CAE 技术进行结构疲劳分析时，Hyper -Works 开放式的软件架构，为结构疲劳分析提供了可能。通过多体系统前处理环境MotionView、有限元前处理环境Hypermesh、多体动力学求解器MotionSolve（或其他）、疲劳分析求解器RADIOSS（或其他）及后处理环境HyperView & HyperGraph 的无缝集成，实现了结构疲劳分析的流程化。

（3）该流程和方法完全可推广到其他多体系统疲劳分析上。

[1]王国军.nSoft 疲劳分析理论与应用指导教程[M].北京：机械工业出版社，2007.

[2]闫思江,李凡国.变杆长参数四杆机构的运动学仿真[J].机械传动，2011,（12）.

[3]洪清泉，等.OptiStruct & HyperStudy 理论基础与工程应用[M].北京：机械工业出版社，2012.

[4]闫思江,杨金凯,赵剑波.供热管道热损失有限元分析[J].河南科学，2013,31（9）.

[5]李凡国,刘广会,闫思江.板料成形拉延筋拉延阻力和变形的有限元预测[J].现代制造技术与装备，2014，（3）.

[6]谈传明，张子东，曹光荣，等.折弯机滑块的有限元分析及优化[J].锻压装备与制造技术，2011，46（6）.

[7]赵博程.电液伺服加载系统四连杆机构控制器设计[J].液压气动与密封，2014，（2）.