基于Petri网的城市交通应急管理系统分析

张晓青，王啟明

(兰州交通大学 交通运输学院，甘肃 兰州 730070)

基于Petri网的城市交通应急管理系统分析

张晓青，王啟明

(兰州交通大学 交通运输学院，甘肃 兰州 730070)

交通应急管理系统是交通安全、可靠性运营的保障，是交通发展战略规划中的重要研究内容。为了能对交通应急管理系统进行定量分析，文章从定性的角度分析了影响交通应急管理的因素，建立了城市交通应急管理系统的Petri模型，并利用随机petri网和模糊集理论对建立的模型进行性能分析，同时根据库所繁忙概率和变迁利用率确定影响应急系统性能的薄弱环节，提出提高该交通应急管理系统性能的改善措施。

交通应急管理系统；Petri网；马尔科夫链；性能分析

0 引言

交通应急管理系统是交通安全和可靠性运营的保障，是交通发展战略规划中的重要研究内容。当有突发事件发生，如遇自然灾害，以及各种交通事故等，这就需要交通管理部门有高效的应急预案，使广大乘客及其工作人员能够得到及时疏解，以最大可能地保证公众生命的安全和减少财产的损失。所以，全面认识和恰当分析城市交通应急管理系统的性能具有十分重要的意义。

交通应急管理系统是有效应对城市突发事件，维护社会稳定，完善社会管理职能的重要系统。交通应急管理系统是一个涵盖了交通应急事件整个生命周期，包括信息检测、信息预报及公布、应急处置等过程技术手段的动态系统。文献[1]在总结国内外应急管理系统现有研究的基础上，阐述了交通应急管理系统的组成子系统和工作流程；文献[2]根据应急事件的形成机理和影响范围的不同将道路交通应急管理系统分为四个方向： 道路自然灾害应急管理、 道路交通重大事件应急管理、 道路交通突发事

件应急管理、道路交通事故应急管理，在此基础上设计了道路交通应急管理系统框架；文献[3]分析公路交通应急资源管理系统的定位以及系统的需求，设计了公路交通应急资源管理的工作流程和系统；文献[4]介绍了城市轨道交通应急管理与处置系统的设想、系统构架的设计和构建方法；文献[5]根据轨道交通突发事件应急决策的特点，将CBR技术应用到城市轨道交通应急处置辅助决策系统。

本文参考文献[1-2]将交通应急管理系统分为以下部分组成：事件检测子系统、事件分析子系统、事件预案管理子系统、事件决策子系统、事件救援子系统以及完成信息传递的通信子系统，各个子系统共同构建交通应急管理系统，系统框架组成如图1所示。参考文献[3-5]以及影响应急事件流程的重要度，可将其简化为三个部分：应急事件信息检测系统、应急事件决策系统、应急事件救援系统。

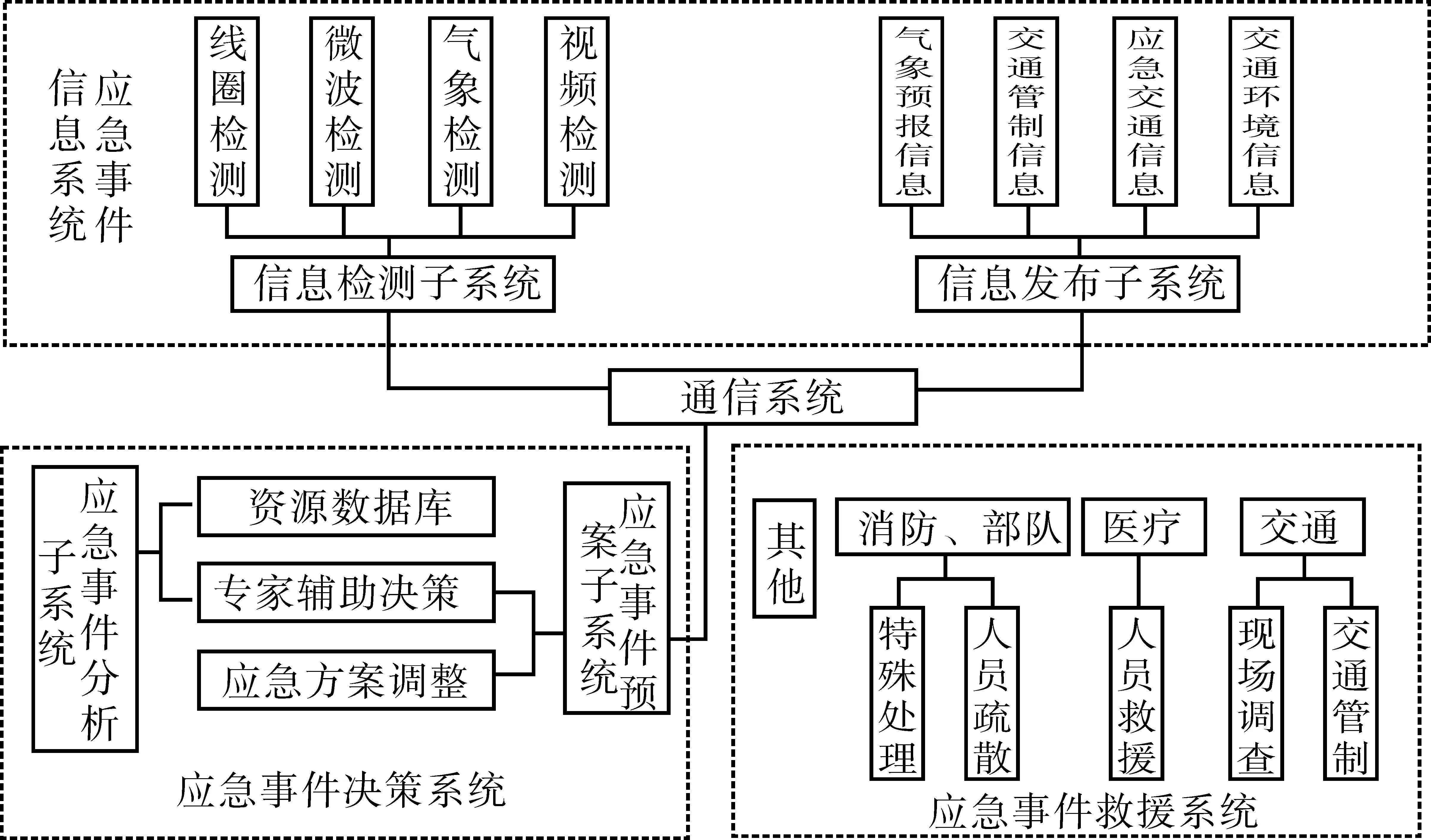
图1 交通应急管理系统构架图

通过分析已有交通应急管理系统的研究和图1可以看出，虽然目前对于应急事件管理工作的研究取得了很多进展，但是，交通应急管理系统由于系统内部各因素的影响还存在以下缺点：

(1) 通应急事件信息获取手段落后；

(2) 应急管理信息化程度低；

(3) 应急预案不完善；

(4) 信息共享程度较低；

(5) 常态化应急机构没有真正建立；

(6) 各部门之间缺乏协同预警指挥。

1 基础理论

1.1 模糊集理论

模糊集是指用于表示界限或边界不分明的具有特定性质事物的集合，模糊数的定义[7]：如果是实数域R上的正常模糊集，且对于任意0≤λ≤1，其截集A是一个闭区间，则称A是一个模糊数。三角模糊函数f(x,a,b,c)描述为：

针对三角模糊数f(x,a,b,c)的λ1和λ2截集有：

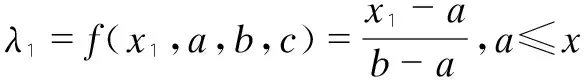
这样就求得x1=a+(b-a)λ1，x2=c-(c-b)λ2则三角型模糊函数f(x,a,b,c)的λ1和λ2截集为[a+(b+a)λ1,c-(c-b)λ2]。当λ1=λ2=λ时，三角模糊数的λ截集为[a+(b-a)λ,c-(c-b)λ]，即三角模糊数的信任区间，如图2所示。

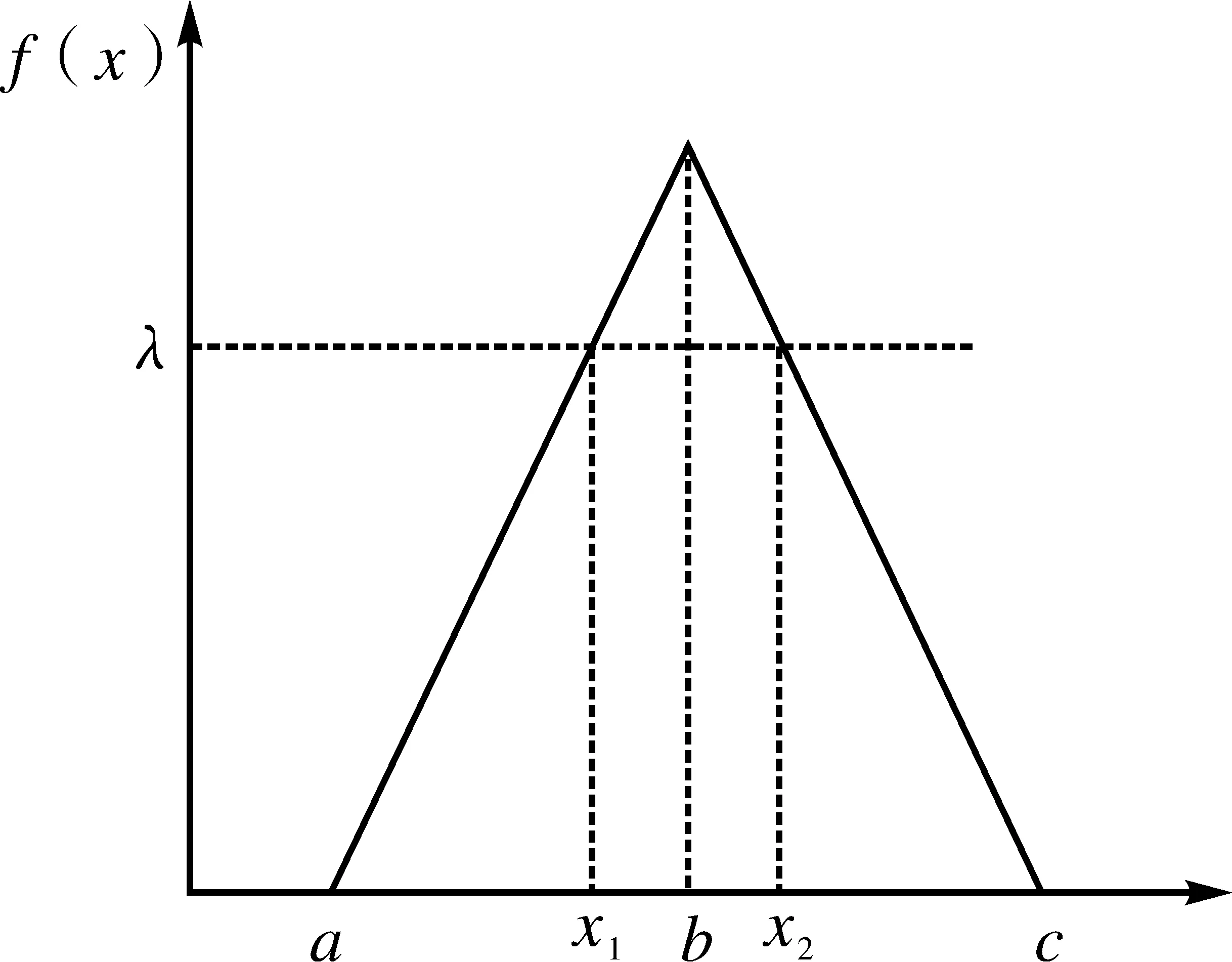
图2 三角模糊数λ截集示意图

1.2 随机Petri网理论

Petri网的概念由德国的CarlAdamPetri在1962年首次提出，由于Petri网融合了形式化定义和图形表示功能，能够简洁、深刻地刻画系统的动态性质，因而越来越受到人们的关注。在经典Petri网的基础上，给每一个变迁关联一个实施速率，引入时间参数，就得到随机Petri网。现给出随机Petri网的定义：

六元组SPN=(P，T，F，W，M，α)

其中：P={p1,p2,p3,…pm}，是库所的有限非空集；T={t1,t2,t3,…tm}，是变迁的有限非空集；F=P·T∪T·P,有向弧的集合，P和T满足P∩T=φ且P∪T=φ；W∶F→N+是弧权函数，N+={1，2，…}；M∶S→N是初始标识，N={1,2,…}；α={α1,α2，…αm}，是变迁平均实施速率集合，α1是变迁的平均实施速率，一般假定服从指数分布。

2 基于Petri网的交通应急管理系统分析

2.1 交通应急管理系统Petri网建模

根据上页图1所示交通应急管理系统的架构图，以及Petri网的基本理论，构建交通应急管理系统的Petri网模型如图3所示：

图3 交通应急管理系统Petri网模型图

其中变量说明如表2所示：

表1 交通应急管理系统Petri网模型库所说明表

表2 交通应急管理系统Petri网模型变迁说明表

2.2 马尔科夫链及稳态概率方程

根据图3给出的交通应急系统的Petri网模型，可以得到与SPN同构的马尔科夫链，见图4。

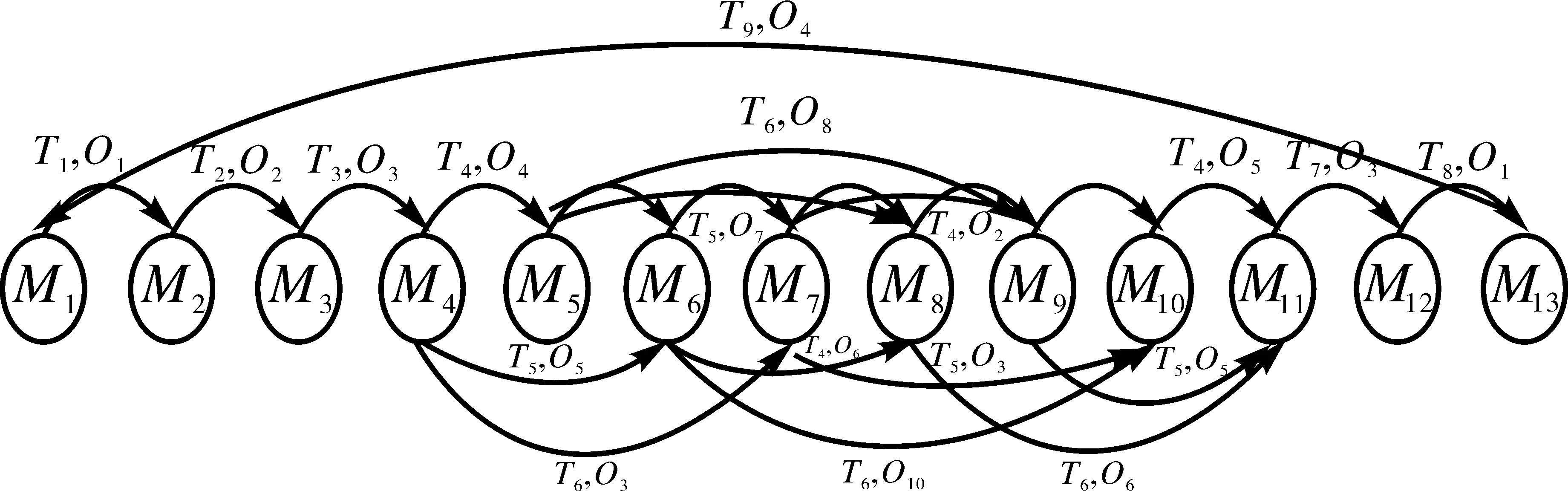
图4 交通应急管理系统马尔科夫链示意图

根据已有的MC得到马尔科夫过程的转移速率矩阵：

设稳定状态概率为x=(x1,x2,x3…x13)从而得到稳态概率方程

2.3 性能分析

对方程中的oi做不同程度的模糊处理，则方程成为模糊稳定概率状态方程，此方程的解就是稳定状态概率。参考文献[12]，选取三角模糊函数，将模糊处理后的速度oi用一个三元组(a,b,c)表示。根据实际情况，由现场调研得到变迁速率o1=o3=4，o2=o6=6，o4=o7=o8=3，o5=2，o9=o10=1。对o1=o3=4、o2=o6=6采用5%的模糊化程度作为其上下界，对o4=o7=o8=3采用10%的模糊化程度作为其上下界。根据实际完成工作情况对o5=2采用15%的模糊化程度作为其上下界，对o9=o10=1采用20%的模糊化程度作为其上下界。则有：

o1=o3=(3.8,4,4.2)；o2=o6=(5.7,6,6.3)；o4=o7=o8=(2.7,3.3.3);o5=(1.7，2，2.3)；

o9=o10=(0.8，1，1.2)。

根据2.1的理论，确定三角模糊数oi的信任区间，篇幅有限，只列出λ=0.5时计算出的稳态概率的信任区间，计算结果如表3所示。

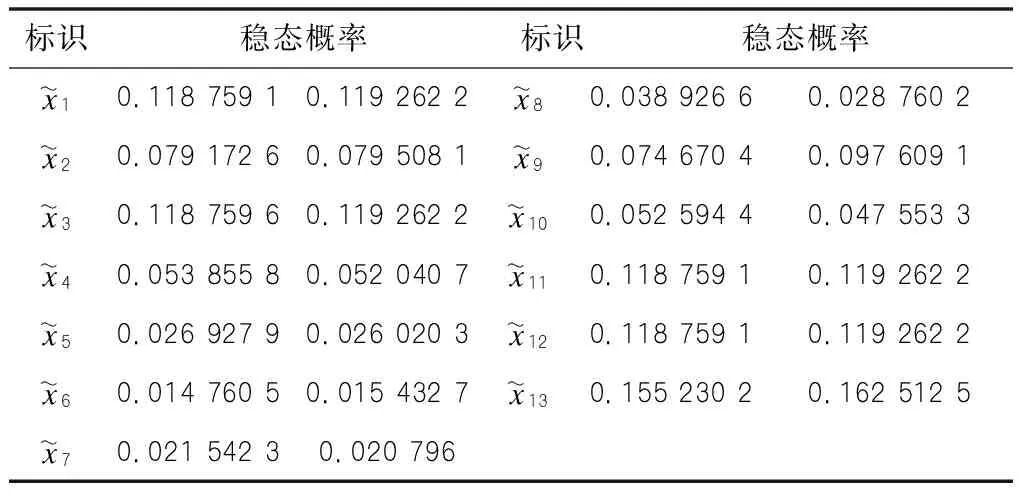
表3 稳态概率的信任区间数值表

[12],利用区域中心法在信任区间求解标识稳定概率值，得x1=0.1190106，x2=0.0793403，x3=0.1190109，x4=0.05294825，x5=0.0264741，x6=0.0150966，x7=0.0211691，x8=0.0338434，x9=0.0861395，x10=0.0500738，x11=x12=0.1190106，x13=0.1588713。

库所繁忙的概率就是交通应急系统中各实体库所处于忙碌状态的概率，库所pi繁忙的概率在这里记为P[m(pi)=1]。首先求得在各标识状态m1,m2,m3…m13下，各库所中的托肯分布情况，具体如表4所示：

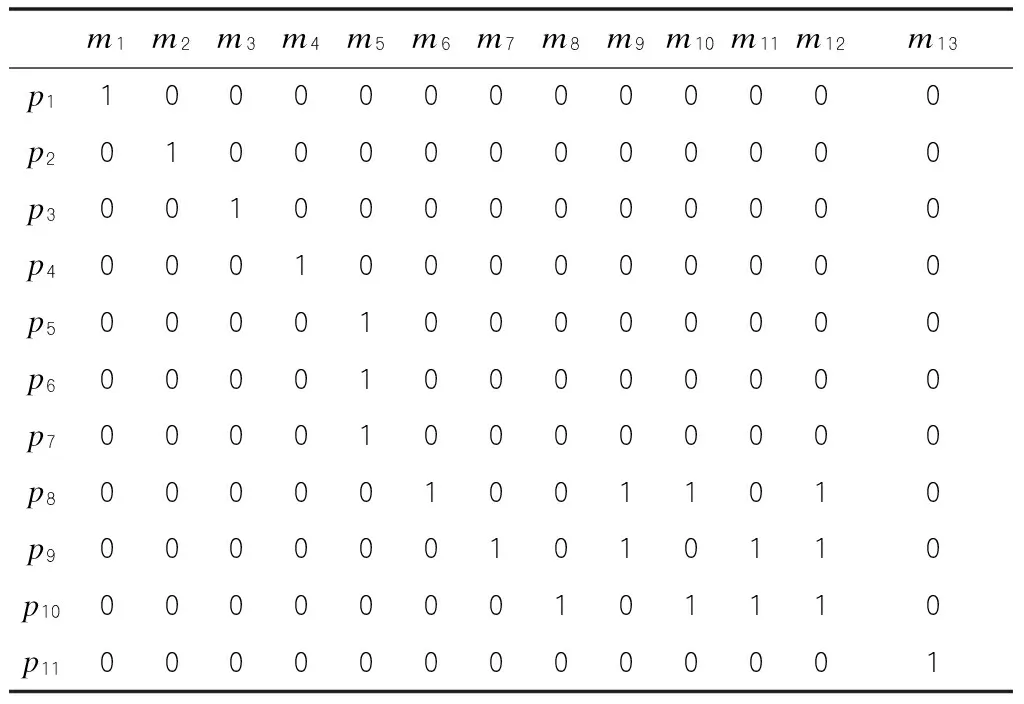
表4 各标识状态下库所托肯分布情况表

各库所繁忙的概率为：

P[m(p1)=1]=x1=0.1190106；P[m(p2)=1]=x2=0.0793403；P[m(p3)=1]=x3=0.1190；

P[m(p4)=1]=x4=0.05294；P[m(p5)=1]=x5=0.0264；P[m(p6)=1]=x6=0.0150；

P[m(p7)=1]=x7=0.0211；P[m(p8)=1]=x6+x9+x10+x12=0.2703；P[m(p9)=1]=x7+x9+x11+x12=0.3453；P[m(p10)=1]=x8+x10+x11+x12=0.3219；

P[m(p11)=1]=x13=0.1588。

变迁的利用率即为使得变迁可实施的所有标识的稳定概率之和，变迁ti的利用率记为U(ti)。

U(t1)=x1=0.1190106；U(t2)=x2=0.0793403；

U(t3)=x3=0.1190；

U(t4)=x4+x6+x7+x10=0.1392；U(t5)=x4+x5+x7+x9=0.1867；

U(t6)=x4+x5+x6+x8=0.1283；U(t7)=x11=0.1190；

U(t8)=x12=0.1190；U(t9)=x13=0.1588。

3 结语

交通应急管理系统是保障交通安全的重要组成部分，健全的交通应急管理系统能够在减少和降低交通安全事故和人员伤亡方面起到重要作用。本文主要考虑系统的时间特性，分析容易产生信息堆积的业务单元，为进一步系统优化提供支持。

从库所繁忙的数据可以看出，库所p8、p9、p10的繁忙概率最大，即系统中专家辅助决策、预案调整、处置信息的传达这些环节最容易产生信息堆积，因此在实际系统的应用过程中，应该加强这几方面的优化。从变迁利用率的数据可以看出，变迁利用率基本持平，其中T5的利用率较高于其他变迁，也就是说人员确认在整个系统中较为繁忙。因此，为了使系统能够做到快速响应、迅速判断、立刻执行，应使各子系统合理分工，密切配合，提高系统的工作效率，当发生交通事故时，才能快速应急。

参考文献

[1]孙 璐,葛敏丽,金姣萍,等.交通应急管理系统发展综述[J].交通运输工程与信息学报，2013,11(1)：1-7.

[2]章锡俏,隋丽娜,李士莲.城市道路交通应急管理框架研究[J].交通与安全，2009,4(194)：138-142.

[3]谭小平,李 为.公路交通应急资源管理系统构建研究[J].物流技术，2012(5)：79-82.

[4]牛卫星.城市轨道交通应急管理系统的研究[J].现代城市轨道交通，2010(6)：9-12.

[5]于鸿飞,秦 勇,王子洋，等.城市轨道应急处置辅助决策系统的研究[J].交通信息与安全，2013,5(31)：163-168.

[6]陆 莹,李启明,周志鹏.基于模糊贝叶斯网络的地铁运营安全风险预测[J].东南大学学报(自然科学版)，2010(5)：1110-1114.

[7]安宗文,祝红林,张 鹏，等.核级蝶阀的模糊故障树分析[J].兰州理工大学学报,2011,37(2):57-60.

[8]刘合香.模糊数学理论及其应用[M].北京：科学出版社，2012.

[9]崔艳萍,唐帧敏,李毅雄.城市轨道交通安全管理体系研究[J].都市快轨交通,2005,18(3):11-14.

[10]张殿业,金 键,杨京帅.城市轨道交通安全研究体系[J].都市快轨交通,2004,17(4):1-3.

[11]张春民,李引珍,陈志忠，等.基于贝叶斯网络的驼峰超速连挂事故分析[J].铁道学报，2011(10)：7-14.

[12]艾厚文.基于随机Petri网的铁路应急预案流程化研究[D].北京：北京交通大学，2008.

Urban Traffic Emergency Management System Analysis Based on Petri Net

ZHANG Xiao-qing，WANG Qi-ming

(School of Traffic and Transportation，Lanzhou Jiaotong University，Lanzhou，Gansu，730070)

Traffic emergency management system is the guarantee of traffic safety and operational reliability，and it is also the important research content of traffic development strategic planning.In order to conduct the quantitative analysis on traffic emergency management system，this article analyzed the factors affecting the traffic emergency management from the qualitative point of view，established the Petri model of urban traffic emergency management system，and by using the random petri net and fuzzy set theory it conducted the performance analysis on established model，meanwhile it determined the weaknesses affecting the emergency system performance based on library busy probability and change utilization rate，and it proposed the improvement measures to improve the performance of traffic emergency management system.

Traffic emergency management system；Petri net；Markov chain；Performance analysis

张晓青，硕士，主要研究方向：交通运输规划与管理；

U

A

10.13282/j.cnki.wccst.2015.06.017

1673-4874(2015)06-0070-04

2015-05-07

王啟明，硕士，主要研究方向：交通运输组织管理优化。

中国铁路总公司科技研究开发计划重大课题(2013X006-A)