平抛运动与斜面结合问题的讨论

宁夏银川市第一中学 刘 丁

一、重视斜面自身的已知条件，如斜面倾角

例1：如图所示，一个物体以v0的速度水平抛出，飞行一段时间后垂直地撞在倾角为θ的斜面上。已知重力加速度为g，不计空气阻力。求：物体飞行的时间。

解：当小球垂直地撞在斜面上时，速度矢量图如下图所示

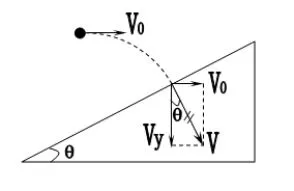
由几何关系知：

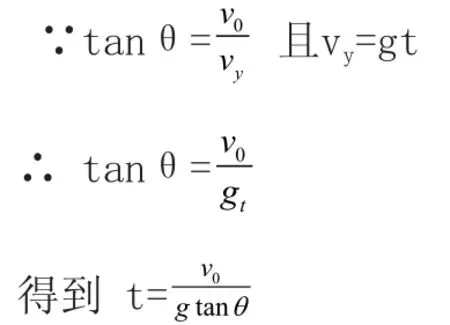
分析：此题在不知道物体做平抛运动时下落高度和水平射程的情况下求解飞行时间，只能根据“物体垂直撞在斜面上”这一条件，利用斜面倾角和速度矢量图进行求解。由此可见，斜面倾角是一个非常关键的条件，所以应该提醒学生遇到此类问题要特别重视斜面的倾角。

二、在重视斜面自身已知条件的前提下，熟练应用平抛运动的规律

例2：如图所示，一个小球以速度v1从斜面顶端水平抛出，假设斜面足够长，当小球撞在斜面上时，其速度方向与斜面的夹角为α1。若小球以速度v2从斜面顶端水平抛出，当小球撞在斜面上时，其速度方向与斜面的夹角为α2。则α1＿α2(填“大于”“等于”或“小于”，不计空气阻力)

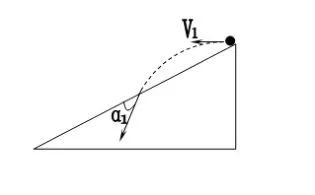
解：假设斜面倾角为θ，不论小球以多大的速度从斜面顶端水平

抛出，最终撞在斜面上的速度矢量图如下图所示

由图可知，小球撞到斜面瞬间的速度方向与水平方向

的夹角为(α+θ)，此过程中小球的位移与水平方向的夹角为θ，

由平抛运动的规律可知

tan(a+θ) = 2tanθ

∵斜面倾角θ是一个定值，∴(α+θ)就是一个定值，则α为一个定值。因此，无论小球以多大的速度从斜面顶端水平抛出，只要又落在斜面上(斜面足够长)，其速度方向与斜面的夹角相等，即α1=α2。

分析：这个问题又一次地告诉我们，当小球从斜面抛出，并且又落回到斜面上，则斜面的倾角是一个不容忽视的重要条件，应该想办法利用它帮助我们解决问题。同时，熟练应用平抛运动的规律也是不可或缺的解题手段。

三、以斜面为参考系可以简化对物体运动的分析，做到熟能生巧

例3：如图所示，一个小球以速度v0从倾角为θ的斜面顶端水平抛出，假设斜面足够长，已知重力加速度为g，不计空气阻力。问：①经过多长时间小球离斜面最远？②离斜面最远时小球的速度是多少？方向如何？③此时距斜面的距离是多少？

解：将小球的水平初速度v0分解到垂直于斜面

和平行于斜面两个方向上；再将重力加速度

分解到垂直于斜面和平行于斜面

两个方向上；如下图所示。

由几何关系可得，

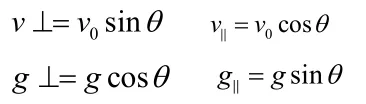
① 小球在垂直于斜面方向上先做正方向(垂直斜面向上)初速度为v0sinθ、加速度为gc osθ的匀减速直线运动，到达最高点(离斜面最远处)后，再做反方向（垂直斜面向下）的初速度为零的匀加速度直线运动。所以，从抛出到小球离斜面最远所需的时间为：

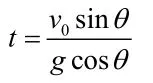
② 小球在平行于斜面方向上做初速度为v0cosθ、加速度为gs inθ的匀加速直线运动，经过t时间平行于斜面的速度为

由于此时小球在垂直斜面方向上的速度为零，所以此时的合速度就等于v∥,方向沿斜面向下。

③ 当小球垂直于斜面的速度为零时，它距斜面的距离最远，此时距离为：

分析：从这个问题我们要获得的方法是：一是对平抛运动进行分解时，不要以为只能分解到水平方向和竖直方向上，我们可以根据需求将它分解到任意两个相互垂直的方向上。二是对曲线运动的研究一定要牢记合运动与分运动的等时性、独立性等特点，根据问题将曲线运动转化为某个方向的直线运动进行求解。

综上所述，平抛运动与斜面结合的问题是有规律可循的，只要熟练掌握平抛运动的特点及规律、重视斜面自身的已知条件，灵活运用运动的合成与分解，就一定能找到解决问题的突破口。