基于船舶阻力计算方法确定浮泥的适航密度值
高志亮,庞启秀,张瑞波
(交通运输部天津水运工程科学研究所工程泥沙交通行业重点实验室,天津300456)
基于船舶阻力计算方法确定浮泥的适航密度值
高志亮,庞启秀,张瑞波
(交通运输部天津水运工程科学研究所工程泥沙交通行业重点实验室,天津300456)
效仿通过船模阻力试验来界定浮泥适航密度值的方法,提出采用船舶阻力计算方法确定浮泥的适航密度值。基于求解NS方程的CFD方法,建立了模拟浮泥中船舶运动流场的数学模型,模型中浮泥的本构关系用改进的Herschel⁃Bulkley模型来描述。以连云港航道现场泥样和超大型油船KVLCC2为例,采用所建立的数学模型计算了船舶以不同速度在不同密度浮泥中航行受到的阻力。通过数学手段分析了船舶阻力随浮泥密度变化的趋势,确定该港口航道浮泥的适航密度值为1 210 kg/m3,该值与采用流变试验方法和船模阻力试验方法得到的适航密度值接近,证明了文章提出方法的有效性。
船舶阻力;计算流体动力学;浮泥;适航密度
在淤泥质河口和海岸地区,浮泥的发育常常导致航道的淤积,给船舶的正常通航带来困难,为此需要定期对航道进行疏浚维护。为了减少航道的疏浚量和疏浚次数,适航水深技术被提出,即利用航道底部密度值较小的浮泥作为可航行水深。如何确定浮泥的适航密度,保证浮泥与船体接触不会造成船舶结构的损坏,或者严重影响船舶的操纵和控制,是应用适航水深技术的关键。
长期以来,浮泥的流变试验是确定其适航密度的实用化方法,被国内外多个港口所采用[1-7]。该方法通过试验测定不同密度浮泥的应力和应变关系,采用宾汉流体模型对试验数据进行外推插值,得到零剪切速率对应的应力,作为浮泥的屈服剪切应力,取密度与屈服剪切应力关系曲线上曲率最大的点所对应的密度值作为浮泥的适航密度值。然而对于密度值低于1 200 kg/m3的浮泥,其抵抗剪切的能力较弱,剪切应力随剪切速率变化的拐点出现得比较晚,采用宾汉模型外推方法得到的屈服剪切应力存在较大的不确定性,从而影响浮泥适航密度值的准确性。
为了弥补流变试验方法的不足,我国颁布的《海港总体设计规范》规定浮泥适航密度值还应通过船模阻力试验的方法来确定,即在不同密度的浮泥中进行船模拖曳试验[8-10],测量船体以不同速度航行时所受的阻力,取浮泥密度与船模阻力关系曲线上曲率变化比较明显的起始点所对应的密度值作为浮泥的适航密度值。船模阻力试验方法原理简单,浮泥的流变特性由船舶的受力特点综合反映,但该方法在实际应用过程中存在着一些缺陷。首先,试验需要有专门的场地和仪器设备,并进行费时费力的系列试验,因而成本较高,效率较低;其次,泥样配制过程繁琐,且使用的浮泥量较大,因而很难保证每组试验浮泥密度均匀一致,使得试验结果的可靠性下降;再次,试验中需要铺设特定密度和厚度的浮泥,因此试验一般在尺寸较小的水槽中进行,而水槽的边壁效应会对船舶阻力产生额外的影响,使得试验结果不能完全反映浮泥特性的变化。
基于计算流体动力学(CFD)方法的数值船池技术[11-13]具有成本低、效率高、重复性好和无外界干扰等优点。在清水中的船舶阻力预报领域,数值船池技术已经跟模型试验方法并驾齐驱[14-16],将该技术代替船模阻力试验方法来确定浮泥的适航密度值已经成为可能。本文以连云港现场泥样和超大型油船KVLCC2为例,应用CFD方法计算船体在不同密度的浮泥中航行所受的阻力,并建立了船舶阻力与浮泥密度的数学关系,通过分析阻力随密度变化的趋势,确定该港浮泥的适航密度值。
1 数学模型
1.1控制方程
浮泥视为不可压缩粘性流体,不考虑浮泥-空气交界面波动和湍流影响,流体的运动由连续性方程和动量方程控制。在笛卡尔坐标系下,控制方程描述如下

式中:脚标i和j采用爱因斯坦求和约定,即相同脚标表示从1至3求和,1、2、3分别代表空间方向的3个分量;x为空间坐标;u为流体速度;ρ为流体密度;P为压力;μ为流体表观粘度。
浮泥为非牛顿流体,其表观粘度随剪切速率变化而变化。本研究采用改进型Herschel-Bulkley(HB)模型[17]描述浮泥的本构关系,该模型表达如下
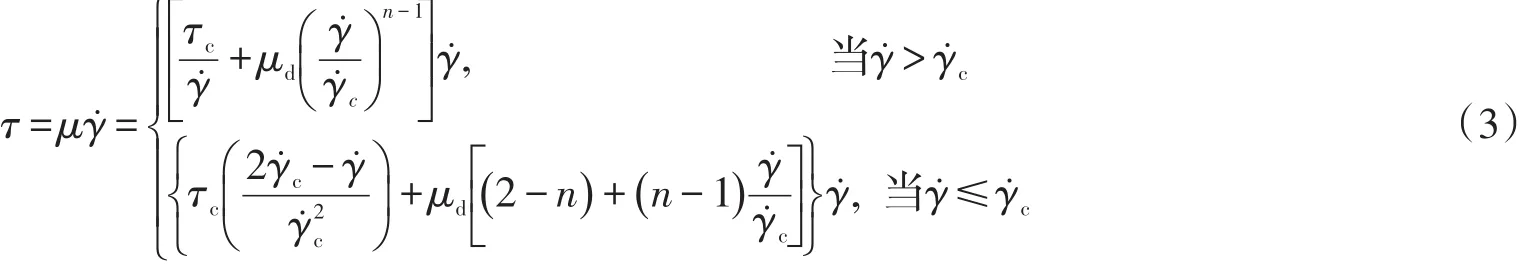
式中:τ为流体剪切应力;τc为流体屈服剪切应力;γ˙为流体剪切速率;γ˙c为流体临界剪切速率;μd为流体动力粘度;n为幂指数。参数τc、γ˙c、μd和n通过浮泥流变试验确定。
由于研究中的船速为中低速,故船体阻力成分将忽略兴波阻力,而只计及摩擦阻力和粘压阻力。当流场中的流体速度和压力求得后,船体所受阻力由公式(4)计算得到。

式中:R为船体阻力;SB为船体表面;n为船体表面法向量;脚标i采用爱因斯坦求和约定;脚标1代表空间沿船长方向的分量。
1.2数值方法
研究中采用通用CFD求解器FLUENT[17]对控制方程(1)和(2)进行求解。通过有限体积法在同位网格上对方程进行离散,其中对流项采用二阶迎风格式,耗散项和压力项均采用中心差分格式。速度场和压力场的耦合通过SIMPLE算法实现。
2 浮泥适航密度值确定
本节将叙述如何基于上述数学模型,采用船舶阻力计算方法代替船模阻力试验方法来确定浮泥的适航密度值。研究中采用的浮泥取自连云港航道,计算船型为超大型油船KVLCC2。目前的计算机性能仍然难以对全尺度(缩尺比1:1)的船舶流场进行模拟,研究中船体的缩尺比为1:45.7。表1和图1分别给出了该船的信息和型线。
首先,将现场取得的浮泥配制成不同密度(1 075~1 406 kg/m3)的泥样,采用R/S-CC流变仪对配制好的泥样进行流变测试,得到剪切应力和剪切速率的关系。对试验数据进行最小二乘拟合,求得HB模型(式(3))中的4个待定参数τc、γ˙c、μd和n,浮泥的本构关系随之确立。图2和图3给出通过流变试验测得浮泥在不同密度下的应力-应变关系以及采用HB模型对试验数据进行拟合后的结果,而模型参数列于表2。可以看出,应力-应变关系曲线上存在一个拐点,该点对应的剪切速率γ˙即为临界剪切速率γ˙c,γ˙c随着浮泥密度增大而逐渐减小。当γ˙<γ˙c时,浮泥的剪切应力随其剪切速率的增大而急剧增大;当γ˙>γ˙c时,剪切应力随剪切速率变化变得平缓。从流变特性来看,浮泥随着其密度增大从牛顿流体向宾汉流体转变。以上所述的不同密度浮泥的流变特点均能被改进的HB模型很好地描述。
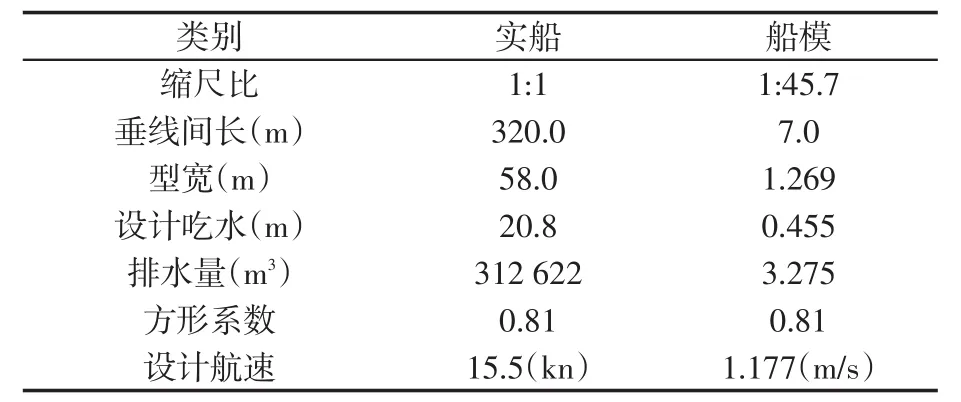
表1KVLCC2船型信息Tab.1Main particulars of KVLCC2

图1KVLCC2船体型线Fig.1Body plan of KVLCC2
接下来采用所建立的数学模型计算KVLCC2油船在浮泥中航行受到的阻力。计算中船速取3种,分别为0.41 m/s、0.83 m/s和1.24 m/s,对应的弗汝德数(Fn)分别为0.05、0.1和0.15。浮泥密度取12种,从1 075 kg/m3增加至1 406 kg/m3,相邻密度差约为30 kg/m3。每次取1种船速和1种密度的浮泥进行计算,共36个计算组次。因为流场关于船舶中纵剖面对称,故只取中纵剖面一侧的流场作为计算区域,图4给出了流场计算域范围及网格划分情况。计算域向上游、下游、侧方和底部分别延伸1倍船长、2倍船长、1倍船长和10倍设计吃水的距离。计算时船体固定在流场中,在上游边界施加速度入口条件,流速与船速大小相同方向相反;在下游边界施加压力出口条件;在上部边界和中纵边界上施加对称条件;其余边界均施加不可滑移固壁条件。计算网格划分时,除了在船首球鼻和船尾桨轴附近区域采用非结构化网格外,其余区域均采用结构化的网格布置形式。船体表面附近网格尺寸为3 mm,远离船体区域网格尺寸逐渐增大,流场网格总数约为71万。
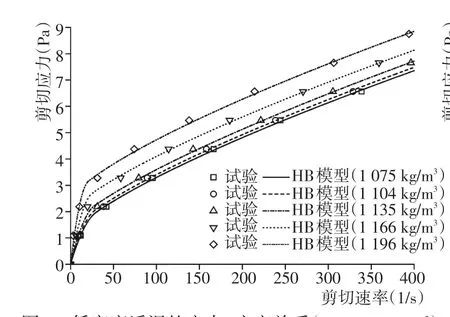
图2低密度浮泥的应力-应变关系(ρ<1 200 kg/m3)Fig.2Rheological behaviour of fluid mud with lower densities(ρ<1 200 kg/m3)
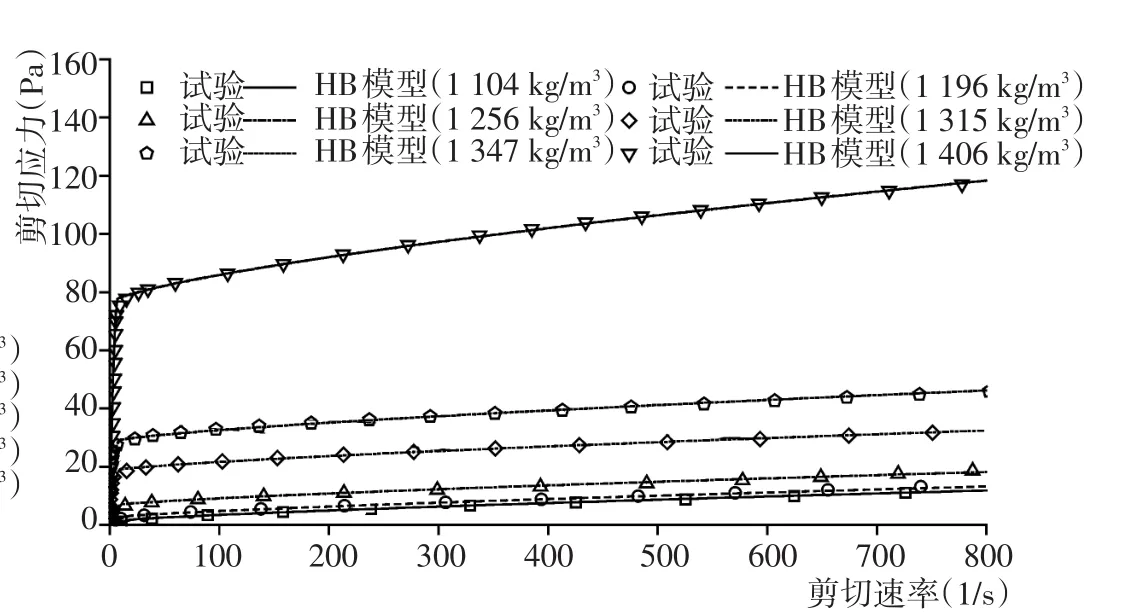
图3不同密度浮泥的应力-应变关系(ρ=1 100~1 400 kg/m3)Fig.3Rheological behaviour of fluid mud with different densities(ρ=1 100~1 400 kg/m3)

表2不同浮泥密度下HB模型参数Tab.2Parameters of HB model for fluid mud with different densities

图4KVLCC2流场计算域及网格布置Fig.4Computational domain and mesh arrangement for KVLCC2

图5不同航行条件下船舶阻力比较Fig.5Comparison of ship resistance in different navigation conditions
图5给出了船体在不同速度和浮泥密度下航行的阻力计算值和采用六次多项式对数据进行拟合的结果。可以看出,船舶阻力随着航速和浮泥密度的增加而增大。在不同航速条件下,根据阻力随浮泥密度变化的趋势,可以将密度值分为(1 050~1 200 kg/m3)、(1 200~1 300 kg/m3)和(1 300~1 400 kg/m3)3个区间。当密度小于1 200 kg/m3时,阻力随密度变化比较平缓;当密度值介于1 200 kg/m3和1 300 kg/m3之间时,阻力随密度增长的比例开始变得明显;当密度值超过1 300 kg/m3后,阻力随密度增大而迅速增加。
正如文献[18]指出,通过观察船舶阻力与浮泥密度关系曲线变化趋势来确定浮泥适航密度值存在较大的人为因素;针对传统方法在理论上的不足,本研究在如何利用船舶阻力与浮泥密度关系上提出了更为可靠的处理方法。前文已经采用曲线拟合的方法得到阻力随密度变化关系的数学表达式,因而可以通过数学计算的方法来得到阻力-密度曲线的曲率,然后取最大曲率所对应的密度值作为浮泥的适航密度值。图6给出了阻力-密度拟合曲线的曲率随浮泥密度的变化,其中数值的正、负号分别表示曲线朝上或朝下弯曲。可以看出,3种不同航速下阻力-密度曲线的最大曲率所对应的密度值非常接近,分别为1 219 kg/m3、1 210 kg/m3和1 216 kg/m3。取上述三者中的最小值1 210 kg/m3作为该流域浮泥的适航密度值,换算成重度值为11.9 kN/m3,该值与文献[10]中通过浮泥流变试验和船模阻力试验综合分析确定的适航重值12.2 kN/m3比较接近,证明基于船舶阻力计算方法确定浮泥的适航密度值是有效的。
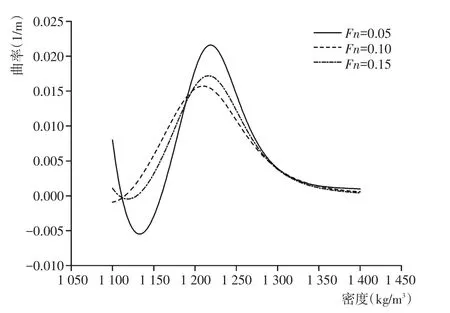
图6不同航速下阻力-密度曲线的曲率随密度变化Fig.6Curvature of resistance⁃density curve changing in function of density for different forward speeds
3 结语
本文基于CFD方法建立了模拟浮泥中船舶运动流场的数学模型,并提出采用数值模拟手段代替物理模型试验手段对船舶在浮泥中航行的阻力进行预报,将数值计算得到的船舶阻力用于浮泥适航密度值的确定。应用本文方法对连云港航道浮泥的适航密度值进行了界定,研究结果表明:(1)数学模型中浮泥本构关系的建立可以通过改进的HB模型并结合流变试验方法实现;(2)采用数学手段分析船舶阻力与浮泥密度关系曲线可以避免传统方法利用该曲线确定浮泥适航密度值的人为主观性;(3)基于船舶阻力计算方法与基于流变试验方法和船模阻力试验方法确定的浮泥适航密度值相吻合;(4)船舶阻力计算方法具有廉价、高效、可靠等优点,可作为现行浮泥适航密度确定方法的一种有益补充。本文仅采用了超大型油船作为计算船型,在下一阶段的工作中将会对其他船型进行计算,以分析不同船型的选用对确定浮泥适航密度值的影响。
[1]陈学良.连云港浮泥测试及“适航深度”的确定[J].水运工程,1998(8):28-31.
[2]陈晓峰,黄建维,刘建军.汕头港外航道适航水深的研究和运用[J].海洋工程,2002,20(4):26-31. CHEN X F,HUANG J W,LIU J J.Investigation and utilization of the nautical depth of the outer navigation channel of Shantou Harbour[J].The Ocean Engineering,2002,20(4):6-31.
[3]钱平生.天津港适航水深下界面淤泥容重值确定与适航水深测量[J].海洋测绘,2002,22(3):35-39.
[4]梅剑云,孙月,李占元.国华台电煤港适航水深应用研究[J].水道港口,2008,29(5):314-317. MEI J Y,SUN Y,LI Z Y.Nautical depth applied to port of Guohua Taishan power plant[J].Journal of Waterway and Harbor, 2008,29(5):314-317.
[5]Wurpts R.15 years experience with fluid mud:definition of the nautical bottom with rheological parameters[J].Terra et Aqua, 2005,99:22-32.
[6]Fontein W F,van der Wal J.Assessing nautical depth efficiently in terms of rheological characteristics[C]//Special Publication of the Hydrographic Society.Proceedings of the 15th International Congress of the International Federation of Hydrographic Societ⁃ies.London:Hydrographic Society,2006:149-152.
[7]Fontein W F,Byrd R W.The nautical depth approach,a review for implementation[C]//Randell R E.Proceedings of the World Dredging Congress XVIII Annual Seminar.Spotsylvania:Western Dredging Association,2007:767-772.
[8]张文忠.不同容重浮泥对船型阻力影响的物理模型试验研究[D].天津:天津大学,2002.
[9]蔡南树,庞启秀,杨树森,等.广州港南沙港区港池适航水深综合论证研究[J].水道港口,2009,30(4):253-256. CAI N S,PANG Q X,YANG S S,et al.Research of nautical depth in harbor basin of Nansha district of Guangzhou port[J].Jour⁃nal of Waterway and Harbor,2009,30(4):253-256.
[10]庞启秀,杨树森,杨华,等.淤泥质港口适航水深技术研究与应用[J].水利水运工程学报,2010(3):33-39. PANG Q X,YANG S S,YANG H,et al.Research and application of the technique of nautical depth in muddy harbors[J].Hydro⁃Science and Engineering,2010(3):33-39.
[11]刘应中,张怀新,李谊乐,等.21世纪的船舶性能计算和RANS方程[J].船舶力学,2001,5(5):66-84. LIU Y Z,ZHANG H X,LI Y L,et al.Calculations of the ship performances and solving of RANS equations in the 21st century[J].Journal of Ship Mechanics,2001,5(5):66-84.
[12]朱仁传,缪国平,向红贵,等.数值水池及其在船舶与海洋工程中的应用[J].上海造船,2007(4):21-23.
[13]Stern F,Yang J,Wang Z,et al.Computational ship hydrodynamics:Nowadays and way forward[J].International Shipbuilding Progress,2013,60(1-4):3-105.
[14]Larsson L,Stern F,Bertram V.Benchmarking of computational fluid dynamics for ship flows:the Gothenburg 2000 workshop[J]. Journal of Ship Research,2003,47(1):63-81.
[15]Carrica P M,Wilson R V,Stern F.An unsteady single⁃phase level set method for viscous free surface flows[J].International Jour⁃nal for Numerical Methods in Fluids,2007,53(2):229-256.
[16]倪崇本.基于CFD的船舶阻力性能综合研究[D].上海:上海交通大学,2011.
[17]ANSYS Inc.ANSYS Fluent User′s Guide[R].USA:Canonsburge,2010.
[18]金镠,虞志英,何青,等.淤泥质港口航道适航密度确定方法的改进[J].水运工程,2013(2):91-95. JIN L,YU Z Y,HE Q,et al.Improvement of method for determining nautical density in muddy harbor[J].Port&Waterway Engi⁃neering,2013(2):91-95.
Determination of nautical density of fluid mud based on ship resistance calculation
GAO Zhi⁃liang,PANG Qi⁃xiu,ZHANG Rui⁃bo
(Tianjin Research Institute for Water Transport Engineering,Key Laboratory of Engineering Sediment,Ministry of Transport,Tianjin 300456,China)
Following the model test for ship resistance measurement,the method based on ship resistance cal⁃culation was proposed to determine the nautical density of fluid mud.The CFD method based on solving the NS equations was applied to calculate the resistance of ship advancing in fluid mud.The modified Herschel⁃Bulkley model was employed to describe the constitutive relation of fluid mud.To test its performance,the proposed method was applied to calculate the resistance of a KVLCC2 tanker in fluid mud dredged from Lianyun port.Based on the mathematical analysis of the changing trend between computed ship resistance and mud density,the nautical densi⁃ty for this port was defined as 1 210 kg/m3,which agreed well with the values defined by the rheology test and ship model test.
ship resistance;CFD;fluid mud;nautical density
U661.31+1
A
1005-8443(2015)04-0285-08
2014-10-11;
2014-11-24
中央级公益性科研院所基本科研业务费专项资金(TKS130201,TKS140201);留学人员科技活动项目择优资助经费
高志亮(1982-),男,广东省人,博士,助理研究员,主要从事计算船舶流体力学研究。
Biography:GAO Zhi⁃liang(1982-),male,assistant professor.

