基于Minitab统计分析软件的地铁车辆车门可靠性评估方法研究

任金宝 邢宗义

（1.中国科学院电子学研究所苏州研究院，215123，苏州；2.南京理工大学自动化学院，210094，南京∥第一作者，硕士研究生）

0 引言

地铁车辆客室自动门系统因其数量多、操作频繁，安全可靠性要求高而成为地铁车辆中的关键部件［1］。车辆客室车门故障率较高，其可靠性和安全性不仅影响了城市轨道交通运营质量和安全效益，更重要的是影响到市民正常的生活和城市的有序运转［2］。

由于地铁车门在地铁车辆安全运营中有着至关重要的作用，国内外学者对地铁车门做了大量的可靠性研究。文献［3］提出应用GO 法原理对地铁车辆客室车门的可靠性特征进行分析，得到导致车门故障的所有可能因素和薄弱环节。文献［4］利用FTA 方法对地铁车辆客室自动门系统在运行中错误打开的故障进行了系统的研究，建立了客室自动门系统的故障树。文献［5］对车门门控器进行控制指令测试和分析，得出了门控器可靠性指标。以上研究为保障地铁车辆安全运营做出了贡献，但所有研究方法中都缺少车门可靠性寿命分析，无法准确预测车门下一时刻的状态。

本文采用 Minitab 统计分析软件中的Anderson－Darling统计量最小原则来确定寿命分布对数据拟合的优劣。首先，筛选车门检修数据，得到车门系统的故障时间，组成样本总体；其次，应用备选失效模型对数据进行分布拟合，依据Anderson－Darling统计量最小原则确定最优分布；然后，采用极大似然估计法计算最优分布参数；最后，通过χ2检验法验证拟合分布的正确性。

1 可靠性分析方法

在可靠性分析研究中，分布模型的种类很多，可靠性工程中用到的分布模型包括 Weibull分布、正态分布等。对于一组未知分布模型的失效数据，通常采用概率纸图法和类WPP图形估计法研究其分布规律。这需要将失效概率或可靠度与失效时间的关系在图纸上绘制出来，得到一条曲线，通过进一步研究曲线的形态，如渐近线、特征点和凸凹性等，确定该失效数据符合何种可靠性分布模型。当不能确定一组失效数据符合哪种分布模型时，可以假设该组失效数据符合所有备选模型，然后对每一种分布模型进行拟合，选取拟合优度最好的分布模型，并进行参数估计和假设检验，验证选取模型的正确性。其过程如图1。［6］

图1 最优拟合模型选取流程图

1.1 数据筛选

地铁车门系统的检修记录数据包括正线车门故障记录和班组检修记录。正线车门故障对列车安全运营和乘客人生安全有巨大的威胁。从某地铁公司获得的检修数据为某条线所有列车的车门故障数据，为了使分析有效，本文选取A2型列车正线故障中非外部因素导致的车门故障为正线车门故障。

1.2 备选分布模型

寿命分布模型中最常用的有Weibull分布模型、指数分布模型、极值分布模型和正态分布模型。

Weibull分布的失效密度函数为：

式中：

α——尺度参数；

β——形状参数；

t——时间。

指数分布的失效密度函数为：

式中：

θ——尺度参数。

极值分布的失效密度函数为：

式中：

μ——位置参数；

σ——尺度参数，σ＞0。

正态分布的失效密度函数为：

1.3 最优模型的参数估计与拟合度检验

1.3.1 拟合优度统计量

用一组失效数据对备选失效模型进行拟合，需要对拟合程度进行评估，以选择最优的拟合模型。Anderson－Darling统计量是统计学中常用的比较数据拟合优劣的统计量之一，具体为概率图中点离拟合直线距离大小的加权平方和，其越靠近分布的尾部，权重越大。Anderson－Darling统计量具体表达式为：

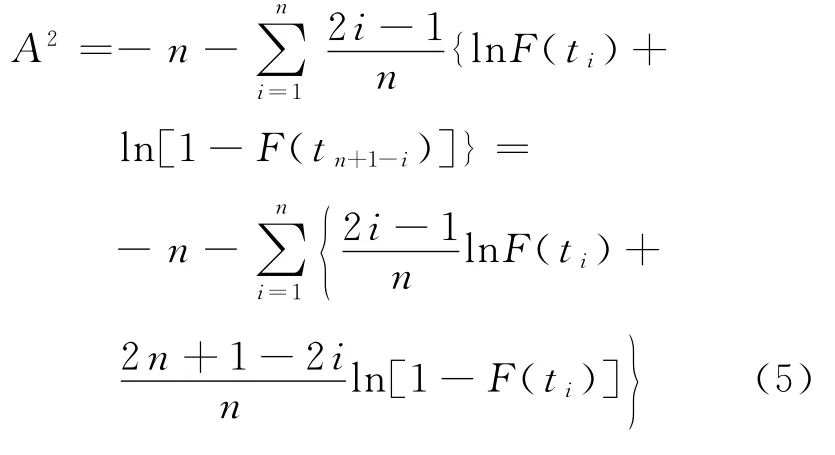
式中：

A——统计量；

i——样本的个数，i＝1，2，…，n；

F（t）——累计失效分布函数；

n——样本总量。

A2的值越小说明分布拟合越好［7］。

1.3.2 参数估计

确定了失效数据的可靠性模型后，对该组数据对应的可靠性模型进行参数估计。Minitab统计分析软件用到的参数估计主要为极大似然估计和最小二乘估计。由于极大似然估计有不变性、相合性、渐近正态性等优良性质，所以较选用极大似然估计。

设样本x1，x2，…，xn的联合密度函数为f（x，θ），其中θ为未知参数，x为样本xi（i＝1，2，…，n）的集合。对于给定的x，称L（θ，x）为θ的似然函数。L（θ，x）＝f（x，θ），若存在θ估计值，使L则称为θ的极大似然估计。

现求解似然方程，即令

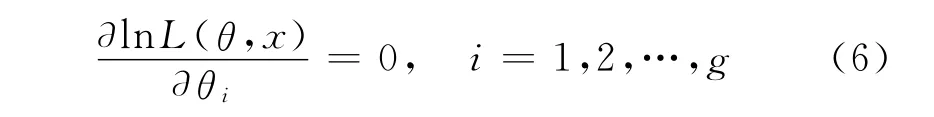
式中，g为未知参数θ的个数［8］。

1.3.3 假设检验

假设检验用以判断原假设的真实性。常用的检验方法有χ2检验法、K－S检验法和P值检验。χ2检验法是统计学中通用的拟合优度检验，本文采用χ2检验法。

设样本总体X（x为X的样本）的分布函数为F（X），根据来自总体的样本检验原假设，设原假设为Ho，则

式中，F0（X）为具体样本的分布函数。

为寻找首先把样本总体X的取值范围分成k个区间（a0，a1），（a1，a2），…，（ak－1，ak），要求ai是分布函数F0（X）的连续点，a0可以取－∞，ak可以取＋∞，记作

其中，pi代表变量x落入第i个区间的概率，且pi＞0。

如果x的样本量为n，则npi是变量x落入（ai－1，ai）的频数。如n个样本值中落入（ai－1，ai）的实际频数为ni，则当H0成立时，（ni－npi）2应是较小的值，因此可以用（ni－npi）2的值来检验H0是否成立。学者皮尔逊证明了，在H0成立时，当n→∞时，χ2检验法的统计量η为

式（9）的极限分布是自由度为k－1的χ2分布。需要检验的母体分布F0（x；θ）中的θ＝（θ1，θ2，…，θm）是m维未知参数，用θ的极大似然估计，即

选择检验统计量为

当n→＋∞时，统计量的极限分布是自由度为k－m－1的χ2分布，在给定的显著性水平γ条件下，若η＞η1－γ（k－1），则拒绝原假设，若η＜η1－γ（k－1），则接受原假设［9］。

2 实例分析

以某地铁公司车门系统为例，筛选此公司A2型车塞拉门系统2年中正线故障记录数据。以车辆架修后投入运营作为起始节点，2年后的时间作为终止节点，得出2年中发生故障的183个车门的无故障时间间隔如表1。表1中无故障时间间隔为起始时间节点到失效时间节点的车门无故障运行时间，频率为相同无故障运行时间的失效车门个数。

表1 车门无故障时间间隔

续表1

首先运用Minitab统计分析软件对表1中所选数据进行分布拟合，其备选分布模型有4种，分别为Weibull分布模型、指数分布模型、极值分布模型、正态分布模型，最终得到4种分布模型的拟合结果如图2所示，Anderson－Darling统计量如表2。

图2 车门寿命概率图

表2 车门失效分布拟合统计量

图2中，分布概率图是比较源数据与拟合曲线之间的接近程度。源数据为图2中的粗曲线。

由表2可知Weibull分布的Anderson－Darling统计量值最小为2.306；从图2中也可看出，Weibull分布的源数据很好地落入拟合曲线95%的置信区间。Weibull分布数据拟合优于其他3个分布模型。Weibull分布的累积失效分布函数为：

其中，β＞0，α＞0。

为了获取Weibull分布的参数，对所选模型进行极大似然估计，得到 Weibull分布的参数估计值β＝2.037 74，α＝396.951。

最后要对模型进行假设检验，确定表1 中A2型车辆车门系统的失效数据是否符合β＝2.037 74，α＝396.951的 Weibull分布。将表1中的97个样本分成10个区间，利用式（9）计算得样本的统计量η＝8.571，取显著性水平γ＝0.01，查有关表格可得η0.99（7）＝18.48，可见＜η0.99（7），所以接受原假设，车门系统的失效数据符合β＝2.037 74、α＝396.951 的 Weibull分布。Weibull分布的累积失效分布函数为：

可靠度函数为：

车门系统可靠度函数图如图3所示。

图3 车门系统可靠度函数图

确定了A2型车车门系统的失效分布模型，计算车门系统给定工作时间的可靠度和在给定可靠度情况下对应的工作时间。

当给定车门系统可靠度R＝0.98和R＝0.95时，由式（11）可知车门系统的可靠寿命为：

假设R＝0.95作为车门可靠度的临界值（即阈值），当车门可靠度降到R＝0.95时，则认为车门故障发生概率加大，即此时车门的可靠度寿命为t＝92 d。分析结果表明，阈值R＝0.95时，应对车门进行一次完全维修。

3 结论

本文通过分析某地铁公司A2型车两车门失效数据，采用Anderson－Darling统计量最小原则确定车门系统的最优拟合分布，得出车门系统失效数据服从Weibull分布。在给定可靠度阈值R＝0.95时，得到车门系统的无故障运行时间t0.95＝92.14 d，与地铁维修部门的现场经验一致，能为地铁公司维修决策提供技术支持。

［1］关明全.城市轨道交通车辆技术与应用［M］.北京：中国铁道出版社，2009.

［2］赖芳盛.地铁列车客室车门可靠性分析及应用研究［J］.中国高新技术产业，2013（8）：39.

［3］董军哲，杨建伟，黄强.基于GO 法地铁车辆客室车门可靠性评价［J］.城市轨道交通研究，2013（4）：28.

［4］王萍，杨保年.基于故障树的地铁车辆客室自动门系统可靠性分析［J］.南京工业职业技术学院学报，2013（2）：47.

［5］Lecomte T.Safe and reliable metro platform screen doors control／command systems［J］.Springer Berlin Heidelberg，2008，5014：430.

［6］侯甲栋，闫锋，李明.基于Minitab的通用航空发动机寿命件可靠性分析方法［J］.航空维修与工程，2013（2）：74.

［7］Adam W G，Ian A W.Approximating the tail of the Anderson－Darling distribution［J］.Computational Statistics＆Data Analysis，2012，56（12）：4301.

［8］朱晓琳，王志刚，夏慧明.非线性系统模型参数估计的差分进化算法［J］.价值工程，2013（10）：178.

［9］王志福，潘旭，金姝，等.假设检验的原理及其应用［J］.渤海大学学报：自然科学版，2013（2）：101.

［10］董军哲，杨建年，黄强.基于GO 法地铁车辆客室车门可靠性评价［J］.城市轨道交通研究，2013（4）：28.