轮轨非线性几何接触对铁道车辆稳定性影响的研究＊

张 海 周新建 王成国 肖 乾 林凤涛

（1.华东交通大学机电工程学院，330013，南昌；2.中国铁道科学研究院铁道科学技术研究发展中心，100081，北京；3.华东交通大学现代轨道车辆研究所，330013，南昌∥第一作者，讲师）

铁道车辆的导向运动主要由轮轨关系所决定，因此，轮轨关系也是研究铁道车辆运动的基础之一。在轮轨关系中，轮对又是最基础的组成部分。传统的轮对有一些独有的特征：轮对由一根刚性的轴连接在一起，因此轮对上的2个车轮都是按照同一个角速度旋转，并且它们之间的距离是不变的；车轮轮缘保持在钢轨内侧边缘，且轮缘与钢轨内侧边缘横向间隙通常在7～10 mm 左右；车轮踏面在横截面上都具有一定的曲率；同样，钢轨顶面在横截面上也具有一定的曲率［1］。尽管在理论上轮轨接触的几何关系是确定的，但是它具有很强的非线性特征，在高速运行条件下其对铁道车辆行车稳定性有很大的影响。

1 轮轨滚动接触几何准线性表示

依据学者Maurer的表述，作为车轮截面半径RW、钢轨顶侧面连接曲线半径RR、接触角δ0、名义滚动圆距的一半e0和名义滚动圆半径r0的线性表述如图1所示。

为了更为简单、高效地描述轮轨的几何接触状态，准线性轮轨接触模型一般有以下3个参数：等效锥度λe、接触角参数ε和滚动参数σ。

图1 轮轨接触线性化表述模型

假设δ0角很小（sinδ0≈δ0，cosδ0≈1），那么式（1）就可简化为

从式（4）可以看出，λe受到δ0和轮／轨轮廓匹配的影响。

准线性的轮轨接触模型参数可以通过简谐线性法进行计算。这种线性化不仅考虑在轮轨平衡位置的非常微小的位移，而且还考虑轮轨之间微小间隙下的特殊位移。学者Polach使用准线性的轮轨接触来计算临界速度（车辆从某速度运行时受外部激励产生振动后，如果振动的幅值不断衰减，则认为车辆运行稳定，若振动出现等幅周期振荡，则此速度称为车辆的临界速度），并讨论了ε角和σ变量对临界速度的敏感性。总的来说，相对于λe对车辆运行稳定性影响的敏感性，ε对车辆运行稳定性影响的敏感性低很多［2］。

等效锥度可以方便反映出轮轨接触的典型几何特征，因此得到了广泛的应用。目前，国际上主要应用以下4种计算等效锥度的方法：

1）简谐线性法；

2）国际铁 路联盟 标准 UIC 519 附 录 B［3］Klingel式的等效线性法；

3）国际铁路联盟标准UIC519附录C 的滚动圆半径差的线性回归法；

4）UK 线性法。

不同方法计算的等效锥度存在差异［4］。轮对横移量3 mm 时的等效锥度定义为名义等效锥度［5］。本文使用Adams／Rail软件中的RSGEO 工具包计算等效锥度，采用了简谐线性法。等效锥度λe的确定要满足以下条件：线性的左右车轮滚动圆半径差与非线性的左右车轮滚动圆半径差之间差值的平方应在一个正弦波（y＝y0sinτ，其中，y为轮对横移值，y0为横移幅值，τ为时间变量）运动周期内的积分为最小，如式（5）所示。

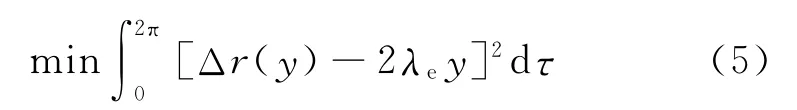
式中：

Δr（y）——左右车轮滚动圆非线性半径差。

对λe求导，得到

这样将非线性关系的Δr（y）折算成线性关系就称为等效线性化，当为谐波运动时称为简谐线性化。

2 轮轨接触非线性几何参数

现在按轮对横移幅值3 mm 时的等效锥度数值作为轮轨接触几何参数。在铁道车辆安全性实践中，等效锥度能反映有关的有用信息。但是等效锥度并没有考虑轮轨滚动接触的非线性几何特性［4，6－7］。

为了解决些问题，有两个参数被提出来用于描述轮轨滚动接触非线性几何特性。

1）能级参数：即等效锥度λe。

2）非线性参数λN：其为等效锥度随轮对横移幅值变化曲线的斜率。

依据国际上最新的研究成果轮对横移幅值为2 mm 和4 mm 下的锥度数值被用于配合幅值3 mm下等效锥度来评价车辆运行稳定性。这三个锥度数值被用来计算非线性参数λN，这也能描述等效锥度随轮对横移幅值的变化情况。在最新版的UIC518标准中，λN常使用轮对横移幅值为2 mm 和4 mm下的等效锥度增加量与轮对横移幅值增加量的比值表示，记为λN，1如式（7）所示。

式中：

λ2——轮对横移幅值2 mm 下的等效锥度；

λ4——轮对横移幅值4 mm 下的等效锥度。

3 轮轨接触非线性几何参数对车辆运行稳定性的影响

为了分析非线性参数对车辆运行稳定性的影响，选取在2010年7月18日和9月5日分别测量的车轮踏面磨耗型面LMaWear1和LMaWear2以及新轮型面LMA。其中，型面LMaWear1为运行10.1万km 时 CRH2103 型车2号车1位车轮型面，型面LMaWear2为运行19.6万km 时CRH2103型2号车1位车轮型面，测量数据来自于Danmark公司的MiniProf测量系统。将这3种车轮踏面磨耗型面与新轨CHN60型钢轨进行匹配，研究轮轨接触的几何参数对车轮运行稳定性的影响。

3.1 轮轨接触几何分析

型面 LMA／CHN60 型新轨匹配、型面 LMa Wear1／CHN60型新轨匹配、型面LMaWear2／CHN60型新轨匹配时的轮轨接触点分布如图2～图4所示。

图2 型面LMA／CHN60型新轨匹配时轮轨接触点分布

从图中2可以发现，型面LMA／CHN60型新轨匹配时轮轨接触点分布均匀，车轮接触点主要分布在踏面平缓处，只有当轮对横移量超过8 mm 时，接触点迅速进入轮缘。

从图3和图4可以发现：磨耗后的型面匹配下轮对型面上接触点明显向轮缘根部移动，钢轨上的接触点也向轨顶边缘处移动；同时接触点变化的跳跃点明显增多，一方面会使得轮轨磨耗不均匀，另一方面还会降低车辆的运行品质。

由图5可知，型面LMA／CHN60型新轨匹配时等效锥度曲线随轮对横移幅值的增大而缓慢递增，当轮对横移幅值超过8 mm 后，等效锥度急剧变大，这可以从图4发现原因，此时的接触点快速进入轮缘根部。而磨耗后型面匹配时，等效锥度经历了先增大再降低，最后再次增大的过程，而且随着运行公里数增加，磨耗不断增加，等效锥度曲线呈现出“凹”形分布，而且不断加大“凹”的程度。

图3 型面LMaWear1／CHN60型新轨匹配时轮轨接触点分布

图4 型面LMaWear2／CHN60型新轨匹配时轮轨接触点分布

图5 3组不同轮轨匹配的等效锥度比较

型面LMA、LMaWear1、LMaWear2的名义等效锥度λ3分别为0.035、0.165、0.163 rad。按照式（7）计 算 出λN，1，分 别 为 0.007 3、0.043 5 和－0.026 5，如表1所示。

3.2 轮轨接触非线性几何参数对车辆运行稳定性的影响

建立CRH2型车辆动力学模型，将轮轨匹配分别 改 为 LMA／CHN60、 LMaWear1／CHN60、LMaWear2／CHN60。其仿真结果的车辆行驶速度分叉曲线如图6、图7、图8所示。发现随着名义等效锥度的减小，会使得分叉曲线向右移动，即线性临界速度和非线性临界速度增大；而在名义等效锥度大致相同的时候，λN，1的变化对车辆的动力学响应有比较大的变化，随着λN，1减小，速度分叉图中轮对横移幅值小的临界速度明显减小。

表1 3组不同的轮轨匹配锥度表 rad

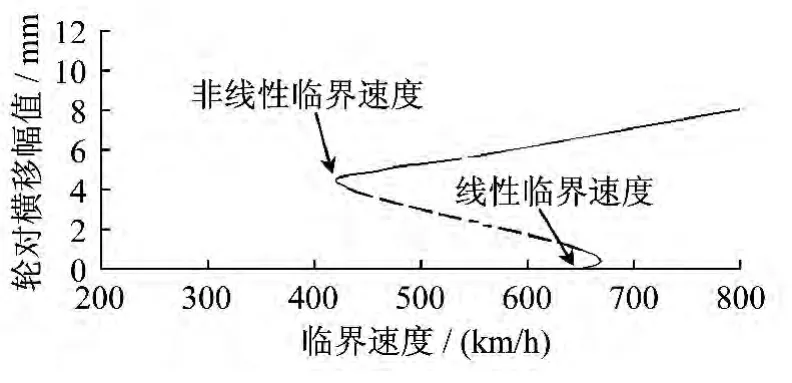
图6 LMA／CHN60匹配下车辆速度分叉图

图7 LMaWear1／CHN60匹配下车辆速度分叉图

图8 LMaWear2／CHN60匹配下车辆速度分叉图

3.3 实测数据分析

从现场试验数据（车辆运行速度为300 km／h，里程从 K99.311 km 至 K102.672 km）的分析也能得到相似的结论，磨耗严重的轮轨型面匹配下的车体和构架振动情况都急剧恶化，同时轮轴横向力均方根值也增加了21.1%，如表2所示。图9、图10、图11和图12分别显示的是车体横向振动加速度对比图、车体竖向振动加速度对比图、构架横向振动加速度对比图及轮轴横向力对比图。

表2 现场试验数据均方根值比较

图9 车体横向振动加速度对比图

图10 车体竖向振动加速度对比图

4 结论

本文分析了轮轨滚动接触的几何线性和非线性参数的表达，并通过车辆速度分叉图讨论了它们对车辆运行稳定性的影响，并得出以下结论：

1）随着名义等效锥度的减小，会使线性临界速度和非线性临界速度增大。

2）在名义等效锥度大致相同时，非线性参数的变化对车辆的动力学响应有比较大影响，随着λN，1的减小，车辆速度分叉图中轮对横移幅值小的临界速度明显减小。

图11 构架横向振动加速度对比图

图12 轮轴横向力对比图

3）从现场试验数据的分析发现，磨耗严重的轮轨型面匹配下的车体和构架振动情况都急剧恶化，同时轮轴横向力均方根值也大幅增加。

［1］柳拥军.高速轮轨接触几何学及高速轮轨几何型面优化的研究［D］.北京；铁道部科学研究院，1999.

［2］Polach O.Comparability of the non－linear and linearized stability assessment during railway vehicle design［J］.Vehicle System Dynamics，2006，44（Supplyment）：129.

［3］UIC519 Method for determining the equivalent conicity［S］.Paris：International Union of Railway，2004.

［4］Polach O.Chapacteristic parameters of nonlinear wheel／Rail contact geometry［C］∥Berg M Trigell，A S.Proceedings of the 21st IAVSD Symposium，Stockholm，2009：95.

［5］Neetter H，Schupp G，Rulka W.New Aspects of contact modelling and validation within multibody system simulation of railway vehicles［J］.Vehicle System Dynamics，1998，28（Suppl.）：246.

［6］Polach O.Application of nonlinear stability analysis in railway vehicle industry［M］∥ Thomsen P.G.True H.Nonsmooth Problems in Vehicle System Dynamics.New York，Springer，2010：15.

［7］刘宏友，曾京，吕可维.高速客车蛇行运动Hopf分叉的研究［J］.工程力学，2005（6）：224.