基于离散Hartley变换的频移键控信号解调算法研究*
戴文辉 梁鉴如
(上海工程技术大学电子电气工程学院,201620,上海∥第一作者,硕士研究生)
近年来,数字化解调理论的研究受到了人们的重视[1]。目前,在软件无线电系统的接收端,一般使用数字化正交解调方式[2]。其基本原理是:将模拟中频信号f(t)首先经过A/D 转换器转化为数字信号f(n);然后用数控振荡器(NCO)产生的两路本振信号再分别与NCO 混频,输出信号经FIR(有限脉冲响应)数字低通滤波器(LPF),得到基本信号l(n)和Q(n),最后解调输出。其主要缺点是要提取同步载波,算法比较复杂、占用存储空间大。
为了满足实时数字化解调技术对算法要求达到计算量小、误码率低的要求,信号的解调方法也有了很大的改进。对于实际应用较为广泛的FSK(频移键控)信号,利用短时傅里叶变换(STFT)来实现其数字解调成为一个研究热点。文献[2-4,6-7]介绍了使用DSTFT(离散短时傅里叶变换)解调FSK信号的方法,同原有的方法相比,具有算法简单、抗干扰能力强的优点。但上述文献中介绍的解调方法在实际应用中都会受到限制。为克服这些缺点,本文提出了一种算法简单、快速的FSK数字化解调算法。
1 离散Hartley变换原理
对于离散的实值数学信号序列{x(n)=0,1,2,…,N-1},离散 Hartley变换(DHT)与反其变换(IDHT)定义为[5]

它表明,时域的N点有限序列x(n)可以变换为频域的N点有限序列X(k)。DHT 的实质就是把一个信号表示成许多不同频率的正弦信号之和,而Hartley变换得到的频域表达式表达的信息与原信号完全相同,只是信号表达方式不同而已。
当对幅值为A,频率为f0,初始相位为φ的正弦波x(t)=Asin(2πf0t+φ),按采样频率fs进行采样,则采样点数N=fs/f0。由此得到信号的主值正弦序列。将它进行DHT运算,可得:
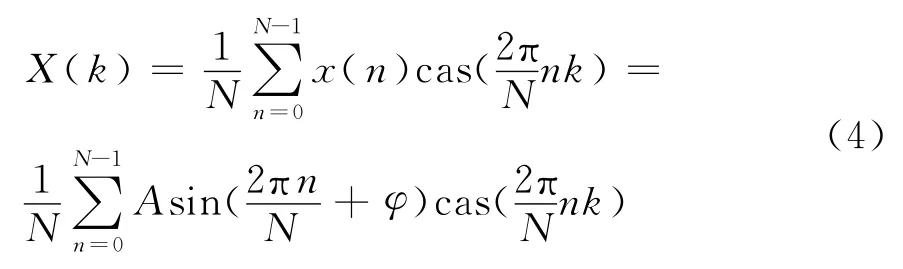
根据该式可以得到频域的离散序列X(0)、X(1)……X(N-1),而当时域波形为正弦函数时,其所对应DHT为一对冲激函数,即只有在基波分量X(1)不为零时,其余分量都为零。则可表示为:
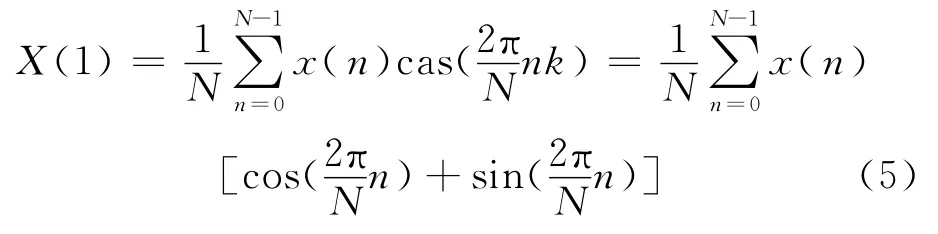
根据频域基波分量可求出正弦信号幅值信息:
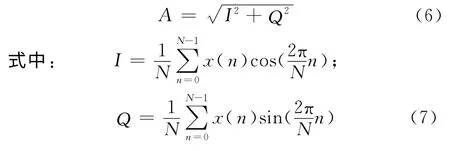
2 基于DHT的FSK数字化解调算法
理想的FSK 信号在码元切换时可能发生载频跳变,使得旁瓣功率较大,需要经过带通滤波后才能发射。其作用是使得码元跳变处的高频成分被滤除。所以实际接受到FSK 信号的码元波形分为两种区域:码元中间部分是稳定区,前、后部分为过渡区。过渡区波形的频率不稳定,且幅度明显降低,而稳定区的波形比较接近于载波频率的正弦波。显然稳定区非常适合对码元进行数字化解调判决。
FSK 信号可表示为:
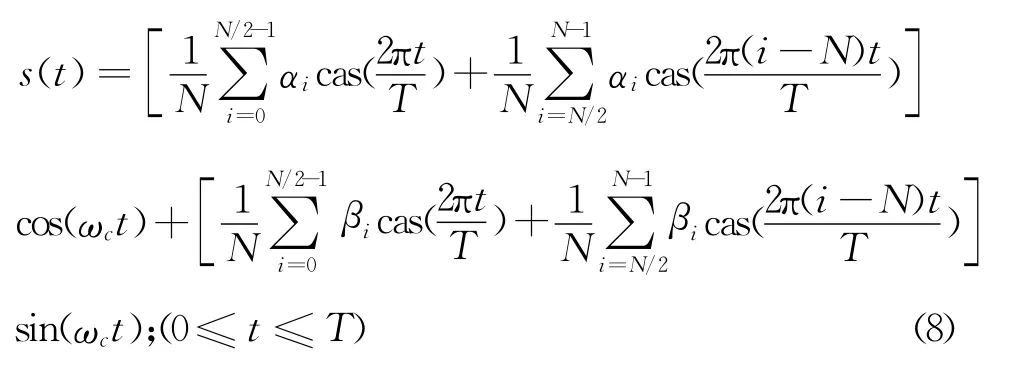
式中:
wc——载波角频率;
T——FSK 信号持续时间;
{α0,α1,…,αN-1}和 {β0,β1,…,βN-1}——N点实数序列。
设FSK 信号载频为f1和f2,采样频率为fs,采样后的样值序列为s(t),n(t)是高斯白噪声序列,则加噪声序列为:R(t)=s(t)+n(t)。
利用DHT原理解调FSK 信号的基本思想为:对接收到的FSK 信号进行采样后,通过两路数字带通滤波器,分别滤出两个载波频率成分。经A/D 转换后,分别对每个码元稳定区内若干个载波周期的N点采样值进行 DHT 解调运算,求出f1和f2分量对应的幅值A1和A2,通过比较其大小来恢复数字码元。当发送的是1码时,由于FSK 信号中1码与0码的波形是正交的,则得到的对应于频率f2的幅值A2应小于A1。同理,如果发送的信号是0码,A1则小于A2。基于 DHT 的 FSK 信号数字化解调框图如图1所示。采用了此解调方法省去了低通滤波,数据抽样的过程使得计算量大大降低。
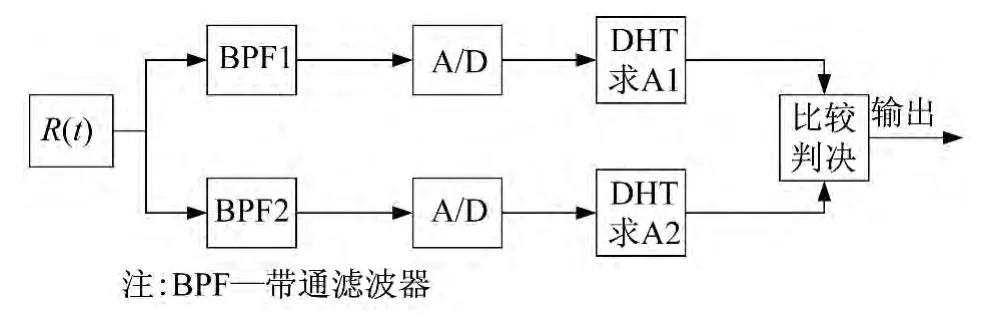
图1 基于DHT的FSK 信号数字化解调框图
为了减小计算的误差,对FSK 信号进行整周期采样即采样的频率为载波频率的整数倍。设每个码元周期的采样点数为N,记为f(1)…f(n);一个码元周期T内,1码有m1个周波(m1=T·f1),0码有m2个周波(m2=T·f2)。对一个码元周期内的采样值分别进行两次DHT 运算,计算出频率f1和f2分量所对应的幅值。用信号码元周期内的采样序列对1码的载波分量进行一次DHT 运算,得到其幅值

再对0码的载波分量进行一次DHT 运算,则可以得到另外一个幅值
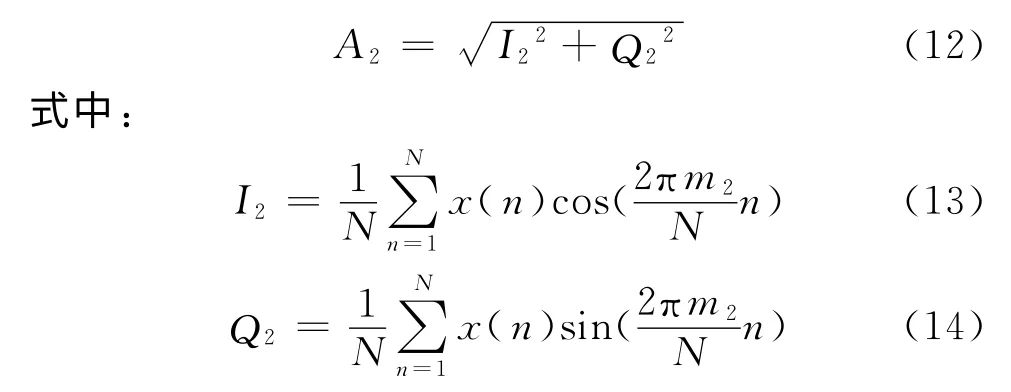
然后,只要对这两个幅值的大小进行比较就可以判决码元了。如果A1>A2,则码元判为1码;如果A1<A2,则码元判为0码[6]。
3 位同步方法
位同步[5]是数字化解调中不可缺少的一个重要环节。在本方案中,分别对两个数字带通滤波器输出的信号进行A/D 转换,再进行DHT 解调,得到两个幅值序列M1(k)和M2(k)。当M1(k)>M2(k)时,说明码元为1;否则码元为0。当M1(k)-M2(k)的值由正数转变为负数或者由负数转变为正数时,可以认为此处为码元的同步点,即M1(k)-M2(k)的极性改变时刻对应于码元切换时刻。根据码元切换时刻就可以调整相位,从而解决位与接受码元之间的同频同相问题,使接收到的码元可以获得正确的判决。
用整数个载波周期的采样值来进行DHT 解调是为了减少“功率谱泄漏”。如果一个载波周期内的采样点数不是整数,则可以用连续几个载波周期内的采样值来进行DHT 解调。而在实际过程中,只需要在预定的位同步时刻前后一段时间内进行M1和M2的计算并判断M1(k)-M2(k)的极性改变时刻即可。
4 软件仿真
为了验证该解调方案的正确性,采用 Matlab软件对整个解调及位同步过程进行仿真。设载波频f1=10 kHz,f2=15 kHz,FSK 信号的码速率为1 kbaud,采样频率fs=120 kHz,T=1 s,数字带通滤波器1和2的带宽均取为2 kHz,码元个数取为10 000个。噪声为宽带高斯白噪声,图2 给出了该解调算法与传统的正交解调算法在不同信噪比下的误码性能比较。从图中可以看出基于DHT 的FSK数字化解调算法的误码率明显减少,说明其抗干扰性能比传统方法有了显著改善。
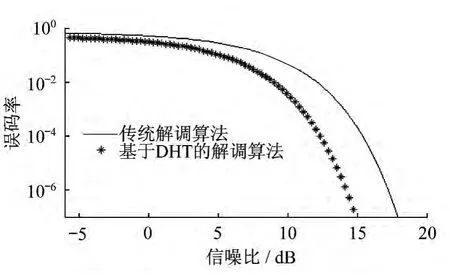
图2 新解调算法与传统算法的误码率比较图
此外,系统对位同步的要求相对没有那么严格,即使在系统位同步发生偏移的情况下依然可以获得较好的解调效果。图3给出了当系统的位同步出现偏移时信号的误码率曲线。
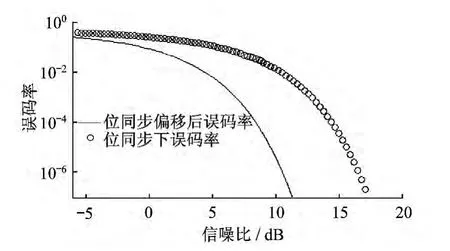
图3 系统位同步偏移情况下误码率比较图
该算法在上海轨道交通2号线TWC(车地通信)系统的应用表明:TWC 系统的信号模块能完成FSK 信号的采集、滤波和放大处理;信号检测装置能完成FSK 信号的解调、误码率分析和处理结果显示以及实时保存;该算法能很好地完成信号检测与通信控制。
5 结语
文中提出的基于DHT 的FSK 信号数字化解调和位同步方法有以下特点:①DHT 是实变换,不需要复数运算,有效地节约了运算时间,提高了运算精度;②在解调时只使用了码元波形稳定区内的采样数据,有利于降低误码率;③编程容易;④不需要载波同步,发射载波的相位波动对误码率影响不大。此种解调方法容易推广到多进制FSK 信号的解调。
[1]杨小牛,楼才义,徐建良.软件无线电原理与应用[M].北京:电子工业出版社,2001.
[2]冯小平,罗明,钟征斌,等.FSK 信号数字化实时解调方法[J].西安电子科技大学学报,2001,28(3):401.
[3]冯小平,李红娟,罗明.用离散STFT 实现FSK 调制信号的数字解调方法[J].西安电子科技大学学报,2001,28(6):812.
[4]胡延平,李纲,王晨,等.一种基于 DSIFT 解调2FSK 信号的新方法[J].通信学报,2000,21(6):54.
[5]Brace well R N .The fast Hartley transform[J].Proc.IEEE,1984,772(8):1010.
[6]胡敏,肖大光.一种MSK 信号的数字化解调新算法[J].计算机仿真,2007(10):23.
[7]吴志敏,黄红兵,肖大光.基于DFT 的FSK 数字化解调算法研究[J].通信技术,2008(11):23.

