K形、V形偏心支撑钢框架抗震性能对比研究

齐永胜 赵风华 李卫青

(1.常州市建设工程结构与材料性能研究重点实验室，常州工学院，常州213002;2.河海大学土木与交通学院，南京210098)

1 引言

偏心支撑钢框架延性优于中心支撑钢框架，可以更好地利用结构的延性抵抗地震作用。K形、V形偏心支撑钢框架是偏心支撑钢框架中的常见类型，两者在设计、制作、用钢量等方面都较为接近，唯一的明显区别是:在支撑跨K形偏心支撑钢框架有1个耗能梁段，V形偏心支撑钢框架有2个耗能梁段。这两种结构的性能已经分别进行了一些研究[1-4]，但目前关于两者性能的比较研究还未见开展。本文采用Pushover方法对这两种形式的偏心支撑钢框架的变形能力、变形特征、耗能能力、极限承载能力的不同和原因进行了研究，并提出了设计建议。

2 Pushover分析结果

为了研究K形、V形偏心支撑钢框架在结构性能方面的差异，本文按我国现行《钢结构设计规范》和《建筑抗震设计规范》设计两种结构各20个，抗震设防烈度为8度、9度。设计地震分组为第一组，场地类别为Ⅱ类。设计基准期和设计使用年限为50年。层数为6层和小于6层的结构用Q235B钢，高于6层的结构用Q345B钢。结构层数为1层、2层、3层、4层、5层、6层、9层、12层、15层、18层;9层及以下结构为单跨，12层、15层、18层结构为3跨。单跨结构布置如图1所示，3跨结构进深(跨度)都为7.2 m，支撑布置于中跨。结构所受荷载见表1，各算例构件规格见附录1.1-1.4。

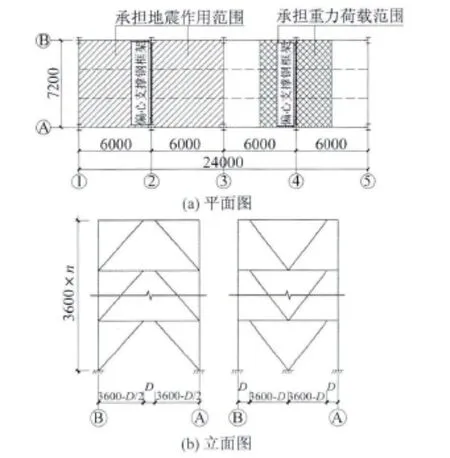
图1 偏心支撑钢框架(单位:mm)Fig.1 Eccentrically braced steel frame(Unit:mm)

表1 荷载Table 1 Loads kN/m2

结构按照FEMAP695建议采用平面模型进行分析;采用LS-DYNA软件建立数值模型，耗能梁段采用Belytschko-Tsay型壳单元模拟;梁、柱和支撑构件采用Hughes-Liu梁单元模拟;结构重量采用Mass单元模拟，集中在梁柱节点处。钢材采用考虑材料失效的双向性强化本构关系。模型的适用性和精度采用10个算例进行验证[5]，此处仅给出文献[6]中3层单跨支撑钢框架推覆试验的模拟结果，如图2所示，从中可看出数值模型能够以令人满意的精度模拟支撑钢框架单调加载试验。

图2 推覆试验的数值模拟Fig.2 Numerical simulation of Pushover test

采用此数值模型用基于位移的推覆方法[7-8]对各算例进行Pushover分析，可以得到推覆曲线充分的下降段。再参照FEMAP695[8-10]对结构水平变形能力和延性的观点，以承载能力曲线上峰值后下降段承载能力退化20%(即80%承载能力尚存)点的位移为结构能发生的极限水平变形控制点，求得结构的最大层间位移角θmax(表2)，可视为结构极限水平变形能力。

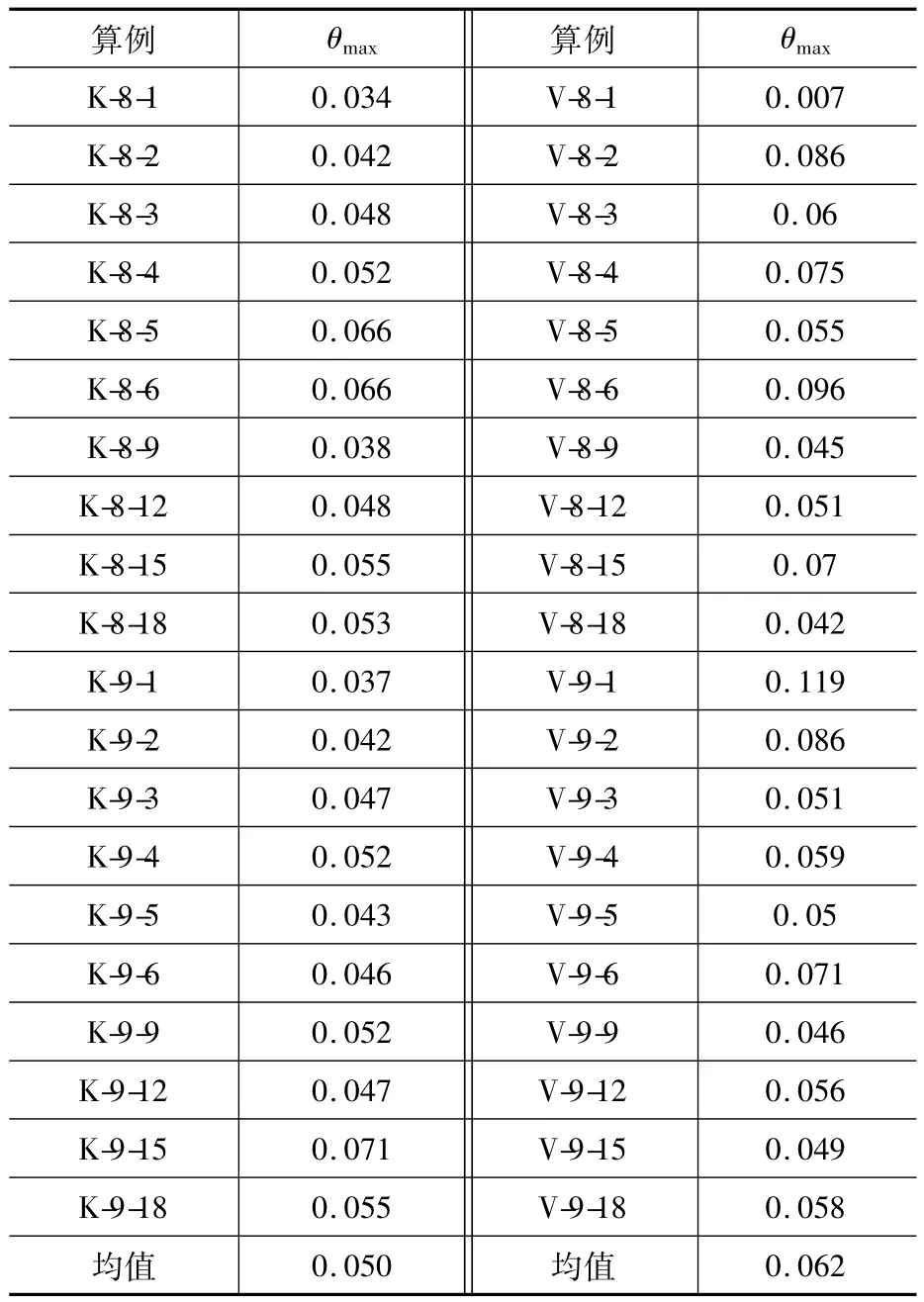
表2 最大层间位移角Table 2 Maximum interstory drift ratios rad

全部算例的最大层间位移角θmax的均值(K形偏心支撑钢框架为0.050 rad，V形偏心支撑钢框架为0.062 rad)可用作结构在强烈地震下的倒塌位移指标限值。

计算最大层间位移角均值时，V形偏心支撑钢框架20个算例中剔除了V-9-1，因为其最大层间位移角超过了 FEMA350[11]、FEMA351[12]规定的抗弯钢框架倒塌水平的最大层间位移角0.1rad的限值，而偏心支撑钢框架的延性要弱于抗弯钢框架，这样大的变形未必能在实际工程中实现。

3 推覆曲线特征

对上述全部算例的推覆曲线进行归纳总结，得到有代表性的偏心支撑钢框架推覆曲线特征如图3(a)所示。推覆曲线可分为3个阶段:从开始加载的原点O点到标志着耗能梁段开始剪切屈服的a点为第I阶段，此阶段为弹性阶段;自a点到结构承载能力峰值点b点为第Ⅱ阶段，此阶段变形特征为耗能梁段剪切屈服，塑性逐渐发展，结构承载能力缓慢、稳定地上升;b点之后至推覆结束点c点为第Ⅲ阶段，b点是受压支撑屈曲点，此阶段由于受压支撑失稳导致其提供的侧向承载能力变小，力学特征为结构水平承载力下降，此阶段结构的水平承载力由受拉支撑、钢框架和受压支撑的残余承载力提供。

图3 支撑钢框架典型推覆曲线Fig.3 Typical pushover curves of BSFs

作为对比，本文也分析了由上述算例改造而成的构件规格相同的中心支撑钢框架的推覆变形，发现中心支撑钢框架由于没有耗能梁段的剪切屈服阶段，水平变形能力较弱，其典型推覆曲线如图3(b)所示，可分为两个阶段:从开始加载的原点O点到结构承载能力峰值点b点，为第I阶段，此阶段结构基本处于弹性状态;从受压支撑屈曲的b点到推覆结束点c点为第Ⅱ阶段。由上述分析可知，偏心支撑钢框架由于比中心支撑钢框架多了一个耗能梁段的剪切屈服阶段(第Ⅱ阶段)，其水平变形能力要大于后者。

在支撑钢框架中，支撑提供了大部分水平刚度。在双重体系中，支撑提供的侧向刚度可以高达75%，在单重体系中可以达到更高比例，所以在受压支撑失稳后，结构承载能力下降较快(图3(a)、图3(b)中的bc曲线段)。

4 耗能梁段数量对变形能力的影响

耗能梁段是偏心支撑钢框架中的“耗能器”和“保险丝”，在强烈地震下能够有效地吸收耗散地震能，其力学性能对偏心支撑钢框架的性能影响极大。

偏心支撑钢框架耗能梁段的数量不同，对结构性能尤其是变形性能的影响也是不容忽视的。由表1中数据可以看出，V形偏心钢框架最大水平变形能力总体大于K形偏心钢框架，其平均值之差为(0.062-0.050)=0.012rad。这一差别主要是由于两种结构的耗能梁段数量的不同造成的:在同一耗能梁跨中V形偏心钢框架有两个，K形偏心钢框架只有一个耗能梁段。

图4画出了单层单跨K形、V形偏心支撑钢框架在水平荷载作用下的变形图，从中可看出由于V形偏心支撑钢框架有2个耗能梁段，在柱顶发生相同水平位移(对应柱端转角θ)的前提下，V形偏心支撑钢框架耗能梁段剪切角γ比K形偏心支撑钢框架小Δγ=(L-D)θ/D-(L/2-D)θ/D=Lθ/(2D)。设耗能梁段长度 D为 L/9，则γV/γK= [(L/2-D) θ/D]/[(L-D) θ/D] =0.438，即V形偏心支撑钢框架耗能梁段的剪切角γV不到K形偏心支撑钢框架耗能梁段的剪切角γK的一半。可见在耗能梁段和其他构件相同的前提下，V形偏心支撑钢框架耗能梁段在达到和K形偏心支撑钢框架耗能梁段相同的剪切角时，V形偏心支撑钢框架耗能梁段允许结构发生更大的水平变形，即V形偏心支撑钢框架具有更大的水平变形能力。

以上通过推覆曲线的特征图说明了中心支撑钢框架和偏心支撑钢框架变形阶段和变形能力的不同。又通过简化的近似分析，说明了V形偏心支撑钢框架(2个耗能梁段)具有比K形偏心支撑钢框架(1个耗能梁段)更大的水平变形能力，下面再通过具体算例进行验证。

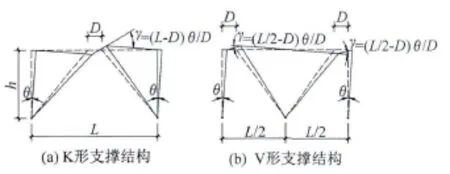
图4 偏心支撑钢框架变形图Fig.4 Deformations of EBSFs

取上述算例中K-8-1、V-8-1单层单跨偏心支撑钢框架进行研究，这两个算例除支撑形式不同外，其他因素完全相同，跨度L=7.2 m，高度为h=3.6 m，耗能梁段长度为D=800 mm，框架立面分别如图4(a)、图(b)中虚线所示。为了对比中心支撑钢框架和偏心支撑钢框架变形能力的差异，中心支撑钢框架对比算例按K-8-1框架取消耗能梁段，将支撑上端移至框架梁跨中相交而成(形成人字形中心支撑钢框架)，如图5所示。3个结构构件都采用常用的国产宽翼缘工字钢，规格相同，柱为I255×250×14×14，梁为I300×300×10×15，支撑为I150×150×7×10。

图5 人字形中心支撑钢框架Fig.5 CBSF with inverted-V brace

3个算例的Pushover曲线如图6所示，从中可以看出偏心支撑钢框架水平位移能力由于多了个耗能梁段剪切屈服阶段而明显大于中心支撑钢框架。

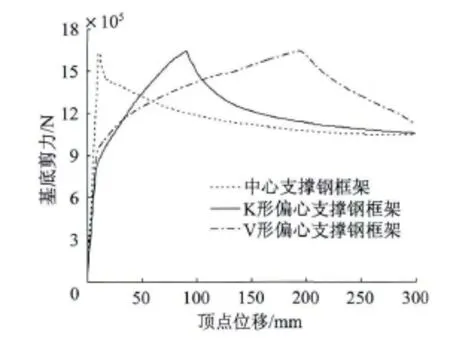
图6 推覆曲线对比Fig.6 Comparison of Pushover curves

同时注意到V形偏心支撑钢框架的耗能梁段剪切屈服阶段的位移值差不多相当于K形偏心支撑的1.8倍，这是因为V形偏心支撑钢框架耗能梁段数量多于K形偏心支撑钢框架，提供了比K形偏心支撑钢框架更大的水平变形能力，这与前面近似分析的结果是一致的。

借助数值分析的动画截图可以更直观地看到上述趋势，图7为3种结构在顶点水平位移为50 mm时的变形图。图7(a)所示人字形中心支撑钢框架受压支撑已经明显弯曲失稳，图7(b)、图7(c)所示偏心支撑钢框架的位移主要由耗能梁段的剪切屈服提供，支撑构件未发生屈曲;同时V形偏心支撑结构中的耗能梁段的剪切变形角要小于K形偏心支撑结构。

图7 支撑钢框架变形图(ux=50 mm)Fig.7 Deformations of BSFs(ux=50 mm)

文献[5]收集国内、外中心支撑钢框架的水平加载试验，得到的该体系最大层间位移角为0.041 rad。综合上述试验成果和本文数值分析成果可认为:在水平变形能力方面:中心支撑钢框架(0个耗能梁段)＜K形偏心支撑钢框架(1个耗能梁段)＜V形偏心支撑钢框架(2个耗能梁段)。为了具有普遍意义，从平均值来看，中心支撑、K形偏心支撑、V形偏心支撑钢框架最大层间位移角分别为 0.04rad、0.05rad、0.06rad;其中的0.04rad是结构变形到支撑失稳程度的变形造成的，0.05 rad比 0.04 rad 多出来的 0.01rad 是 K形偏心支撑钢框架的1个耗能梁段对结构延性的贡献，0.06 rad 比0.04 rad 多出来的0.02rad 是 V形偏心支撑钢框架的2个耗能梁段对结构延性的贡献。由此可见:每个耗能梁段对结构延性做出了大约0.01rad层间位移角的贡献。

5 极限水平承载能力的差异

图6推覆曲线的顶点直观表征了结构的极限水平承载能力。从弹性小变形分析的角度讲，3个算例的极限水平承载能力的差异，与支撑倾斜角度有关，可以由线弹性分析近似说明。人字形中心支撑钢框架、K形偏心支撑钢框架、V形偏心支撑钢框架中支撑与水平线的夹角α依次增加，因而其提供的水平分力2 Ncosα(假定受压支撑和受拉支撑承受的轴向力相等，都是N)依次减小，具体计算结果见表3。3种支撑形式提供的极限水平抗力比例为1.15∶1.08∶1.00。

表3 极限水平承载能力Table 3 Ultimate horizontal bearing forces

但本文分析为弹塑性大变形分析，另外两个因素也影响着结构的极限水平承载能力，一是钢材为双线性强化本构，随着结构变形的增大材料强度提高会使结构极限水平承载能力有所增大;二是随着结构水平变形增大，P-△效应逐渐增大，有使水平极限承载能力降低的趋势。

上述因素综合作用，导致3个算例的水平极限承载能力很接近:中心支撑、K形偏心支撑和V形偏心支撑钢框架分别为1627、1640和1642 kN，相对比例为 1.00∶1.01∶1.01，相差不超过1%。

6 耗能能力比较

图8中给出了两种偏心支撑钢框架典型算例K-8-1、V-8-1水平推覆到承载能力退化到最大承载能力的80%时的塑性耗能。此时，K形偏心支撑结构的顶点水平位移值为122.5 mm，塑性耗能为161503J;V形偏心支撑结构的顶点水平位移值为252.4 mm，塑性耗能为358643J。由此可见V形比K形偏心支撑钢框架耗能能力高1.22倍。虽然这只是一个比较典型的算例，而且结构在强烈地震下的动力反应远比静力推覆复杂，但仍可相信:有两个耗能梁段的V形偏心支撑钢框架具备比只有一个耗能梁段的K形偏心支撑钢框架更出色的抗震性能。

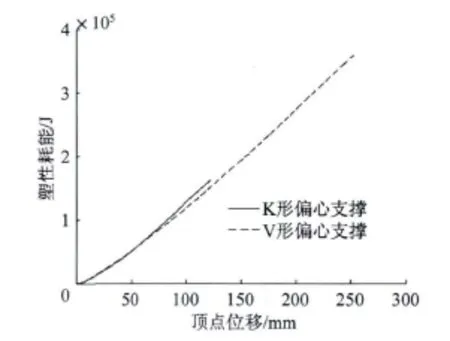
图8 偏心支撑钢框架塑性耗能图Fig.8 Plastic energy dissipation of EBSFs

7 结论

本文设计了典型K形、V形偏心支撑钢框架各20个，通过Pushover分析进行研究，比较了两种结构在变形能力、极限承载能力和耗能能力方面的差异，并与相应的中心支撑钢框架进行了对比，研究表明:

(1)偏心支撑钢框架水平位移能力由于多了个耗能梁段剪切屈服阶段而大于中心支撑钢框架。V形、K形偏心支撑钢框架的水平极限变形能力用最大层间位移角表示，可分别取为0.05 rad和0.06 rad，可作为结构在强烈地震下的倒塌判据使用。

(2)有两个耗能梁段的V形偏心支撑钢框架比只有一个耗能梁段的K形偏心支撑钢框架有更强的变形能力(其最大层间位移角约大0.01 rad)，更大的塑性耗能能力(塑性耗能能力大1倍以上)，因而有更好的抗震性能;又由于两者用钢量基本相等，造价非常接近，所以建议在实际工程中优先选用V形偏心支撑钢框架。

附录1.1 8度设防偏心支撑钢框架Appendix 1.1 Dimensions of EBSFs of seismic fortification intensity 8(9-story and below) mm

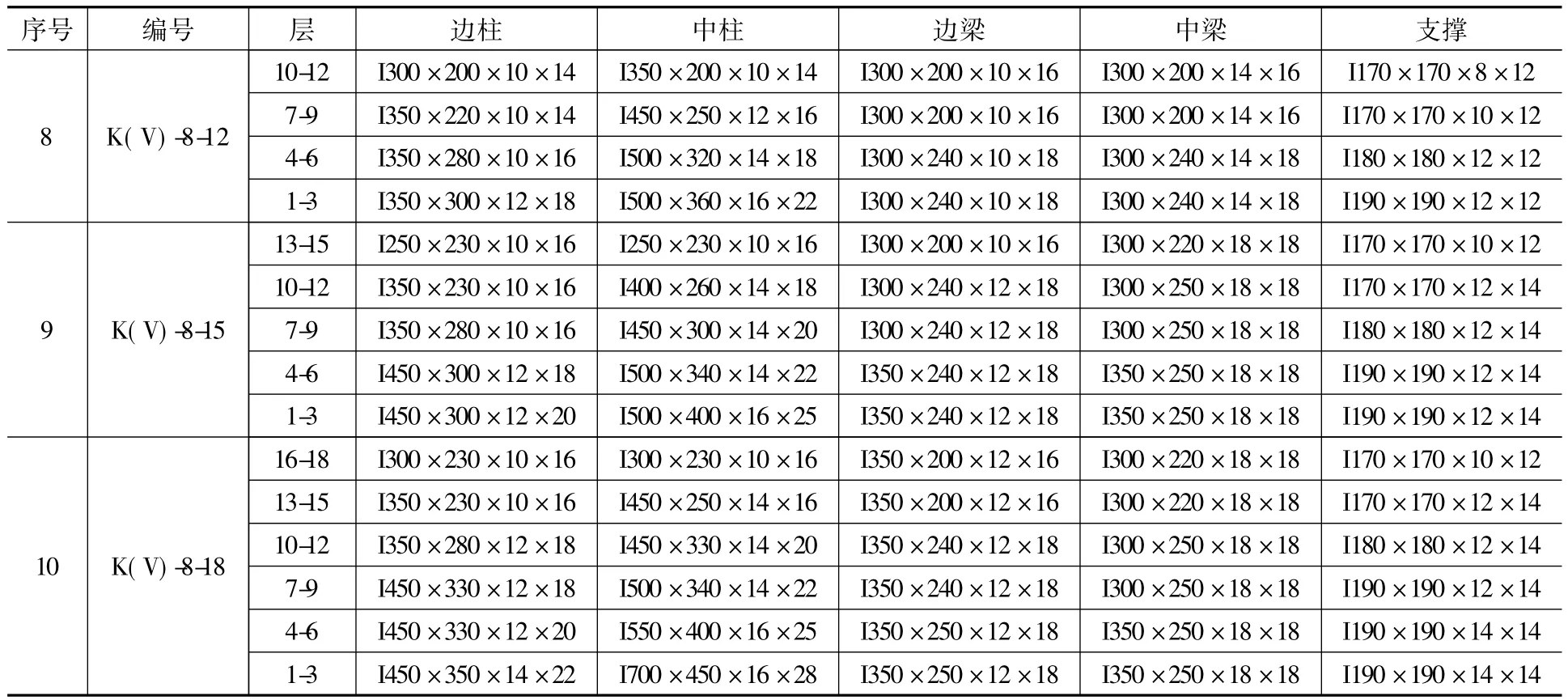
附录1.2 8度设防偏心支撑钢框架(12层、15层、18层)Appendix 1.2 Dimensions of EBSFs of seismic fortification intensity 8(12，15，18-story) mm

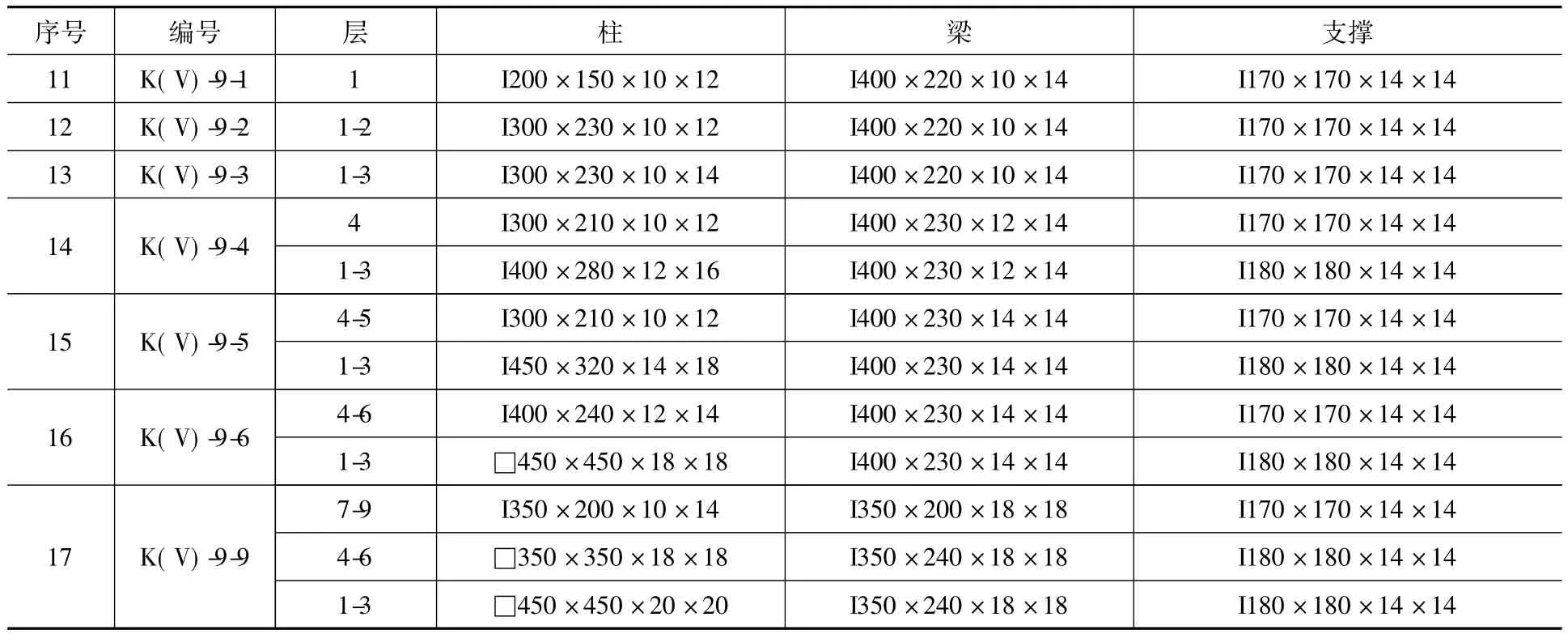
附录1.3 9度设防偏心支撑钢框架(9层及以下)Appendix 1.3 Dimensions of EBSFs of seismic fortification intensity 9(9-story and below) mm

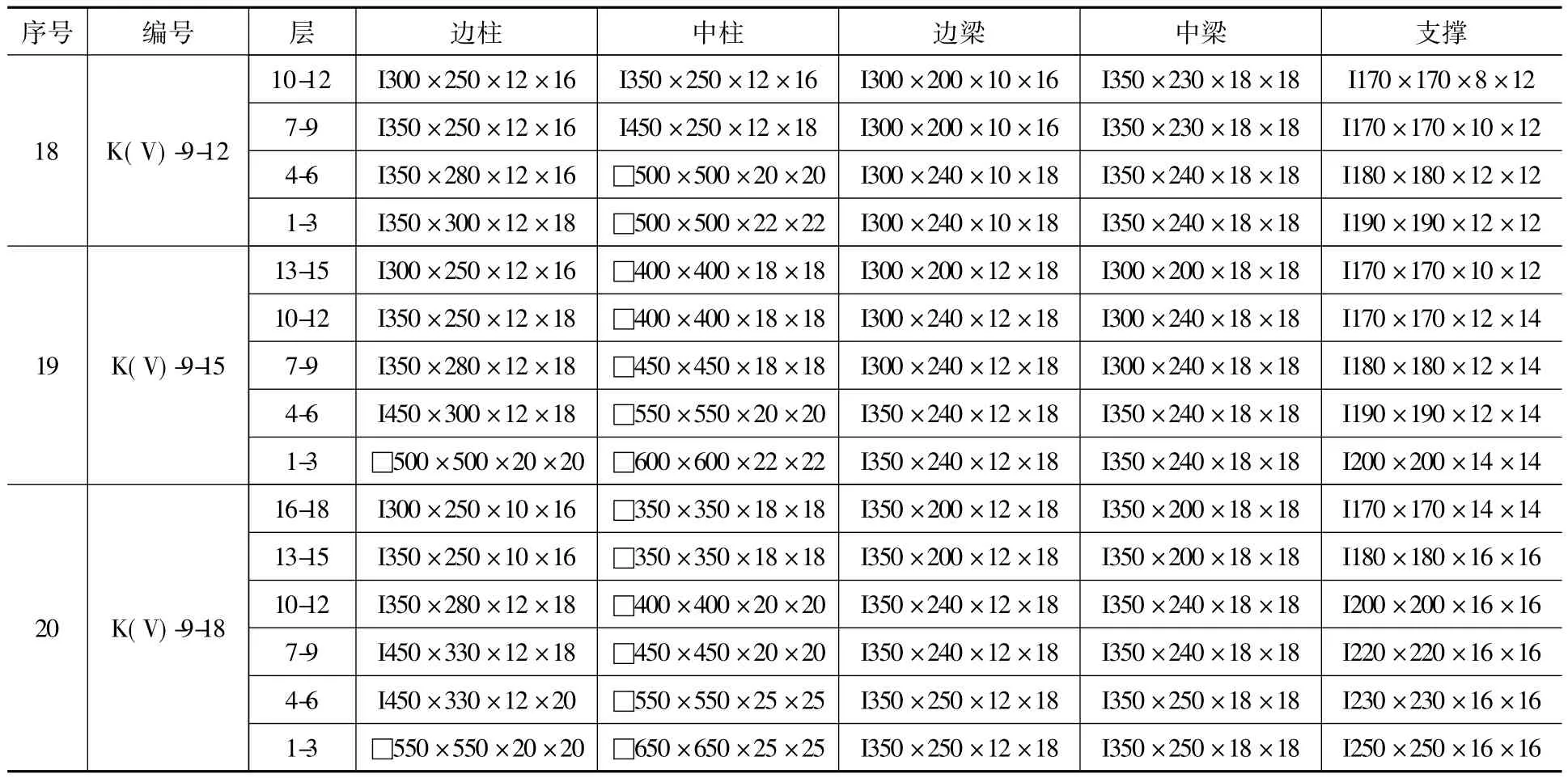
附录1.4 9度设防偏心支撑钢框架(12层、15层、18层)Appendix 1.4 Dimensions of EBSFs of seismic fortification intensity 9(12，15，18-story) mm

[1] 庄晓勇.K型偏心支撑钢框架在循环荷载作用下的性能研究[D].苏州:苏州科技学院，2006.Zhuang Xiaoyong.Study of K shape eccentrically braced steel frames under cyclic load[D].Suzhou:Suzhou College of Scinence and Technology，2006.(in Chinese)

[2] 方飞虎.V型偏心支撑在循环荷载作用下的滞回性能研究及设计建议[D].苏州:苏州科技学院，2008.Fang Feihu.The analysis and design criteria of V style eccentrieally braced steel frames under cyclic load[D].Suzhou:Suzhou College of Scinence and Technology，2008.(in Chinese)

[3] 方飞虎.V型偏心支撑钢框架在循环荷载作用下的滞回性能分析[J].平顶山工学院学报，2008，17(2):45-48.Fang Feihu.Hysteretic behavior study of V-type eccentrically braced steel frames under cyclic loading[J].Journal of Pingdingshan Institute of Technology，2008，17(2):45-48.(in Chinese)

[4] 任云峰，顾强.K形偏心支撑钢框架结构影响系数[J].苏州科技学院学报，2008，21(2):1-5.Ren Yunfeng，Gu Qiang.Structural influencing coefficient of K-eccentrically braced steel frames[J].Journal of University of Science and Technology of Suzhou，2008，21(2):1-5.(in Chinese)

[5] 齐永胜.考虑结构影响系数的支撑钢框架抗震倒塌富余度研究[D].南京:河海大学，2014.Qi Yongsheng.Research on seismic collapse margin ratio of braced steel frame considering structural influencing coefficient[D]Nangjing:Hohai University Dissertation，2014.(in Chinese)

[6] 杨俊芬.中心支撑钢框架的结构影响系数和位移放大系数研究[D].西安:西安建筑科技大学，2009.Yang Junfen.Research on response modification factor and displacement amplification factor of concentrically braced steel frames[D].Xi’an:Xi’an University of Architecture and Technology，2009.(in Chinese)

[7] 李琪.基于位移模式结构抗震设计方法研究[D].南京:河海大学，2005.Li Qi.Research on structure design method based on displacement mode[D]Niajing:Hohai University，2005.(in Chinese)

[8] FEMA P695.Quantification of building seismic performance factors[S].Washington，D.C.，2008

[9] 欧阳倩雯.新型中心支撑钢框架抗震性能研究[J].结构工程师，2013，29(6):92-97.Ouyang Qianwen.Seismic performance a new-type concentrically braced steel frame[J].Structural Engineers，2013，29(6):92-97.(in Chinese)

[10] 包恩和.多层屈曲约束支撑钢框架抗震性能研究[J].结构工程师，2013，29(6):98-105.Bao Enhe.Seismic response of multi-layer buckling restrained braced steel frame[J].Structural Engineers，2013，29(6):98-105.(in Chinese)

[11] FEMA 350.NEHRP recommended seismic design criteria for new steel moment-frame buildings[S].2000.

[12] FEMA 351.Recommended Seismic evaluation and upgrade criteria for existing welded steel moment-frame buildings[S].2000.