输电线路覆冰厚度的概率分布模型比较分析

陆益锰, 安旭文, 刘智勇, 温浩源

(武汉大学土木建筑工程学院，湖北武汉 430072)

输电线路覆冰厚度的概率分布模型比较分析

陆益锰, 安旭文, 刘智勇, 温浩源

(武汉大学土木建筑工程学院，湖北武汉 430072)

根据1959～1983年间湖北恩施绿葱坡和1940～1999年间捷克Studnice覆冰观测站的年最大覆冰荷载观测数据，文章分别按正态分布、极值Ⅰ型、极值Ⅱ型和极值Ⅲ型分布以及PearsonⅢ型指数分布模型进行拟合，并采用柯尔莫戈洛夫法检验了拟合度最优的概率模型；基于拟合的各概率模型，对上述两个区域在不同重现期的覆冰厚度进行了计算分析。根据覆冰厚度概率模型拟合度检验和不同重现期覆冰厚度的计算结果，笔者建议对于重冰区的输电线路或缺少覆冰资料的地区，覆冰厚度宜采用极值Ⅱ型分布函数拟合；对于普通覆冰区的输电线路，覆冰厚度宜采用极值Ⅰ型分布函数拟合。

输电线路； 覆冰厚度； 概率分布模型； 拟合度检验

电网运行过程中，覆冰荷载和风荷载是影响输电线路结构安全性的两个主要因素。2008年初，我国南方大部分地区遭遇历史上罕见的冰雪灾害，给国民经济造成了巨大的经济损失[1-2]。因此，为保证我国输电线路铁塔结构在冰冻雨雪等恶劣气候环境条件下的正常运行，研究如何科学地确定输电线路设计覆冰荷载对输电线路的安全、经济运营具有十分重要的现实意义。

我国电力行业标准DL/T 5440-2009《重覆冰架空输电线路设计技术规程》[3]参照国际电工协会标准IEC 60826:2003 Design criteria of overhead transmission lines[4]的有关规定，认为覆冰荷载与风荷载一样，如果按年最大值统计，其分布规律与理论的极值Ⅰ型分布吻合较好。此外，在观测资料缺乏时，DL/T 5440-2009规定应通过对附近已有线路的覆冰调查分析确定相应的覆冰厚度。DL/T 5158-2012《电力工程气象勘测技术规程》[5]规定，工程地点或与工程地点的地理、气候类似的区域具有10年以上年最大覆冰观测资料，应采用频率分析法确定设计覆冰厚度，然后考虑具体地形影响因素用于输电线路工程结构的设计。覆冰频率计算模型可采用Pearson Ⅲ型分布或极值I型分布。国际电工协会标准IEC 60826:2003、加拿大标准协会标准CAN/CSA-C22.3 NO.1-01 Overhead Systems[6]推荐采用极值Ⅰ型分布作为覆冰荷载的概率统计模型。但IEC 60826:2003同时也指出，并不是所有区域的覆冰概率模型都与极值Ⅰ型分布相吻合，还需要利用观测数据对覆冰概率模型进行适当地调整。可见国内外相关规范对于覆冰荷载的概率分布类型还持有不同意见。

由于我国缺乏长期的覆冰厚度气象观测数据，根据目前搜集到的我国湖北恩施绿葱坡观测站1959～1983年期间和捷克Studnice覆冰观测站1940～1999年期间的年最大覆冰厚度观测数据[7-8]，本文分别采用正态分布、极值Ⅰ型、极值Ⅱ型、极值Ⅲ型以及PearsonⅢ型指数分布模型拟合覆冰荷载的概率模型，并采用柯尔莫戈洛夫检验法进行检验。

1 输电线路覆冰厚度的计算方法

导线覆冰荷载计算主要是确定设计采用的覆冰厚度和覆冰密度以及输电线路覆冰厚度的重现期。本文主要研究覆冰厚度的概率分布模型以及不同重现期的覆冰厚度。

1.1 输电线路覆冰厚度的重现期

我国现行国标《110～750kV架空输电线路设计技术规程》GB 50545-2010[9]规定，设计气象条件应根据输电线路沿线气象资料的数理统计结果及附近已有线路的运行经验确定。以年最大覆冰厚度作为统计样本对覆冰厚度进行统计，假设设计覆冰厚度的重现期为T年，则1/T为每年实际冰厚超过基本设计覆冰厚度的概率，故每年不超过设计覆冰厚度的概率或保证率Fu为：

(1)

DL/T 5158-2012规定，架空输电线路覆冰厚度的重现期可根据输电线路的电压等级按表1确定，各电压等级覆冰厚度的观测点均为离地10m高度。

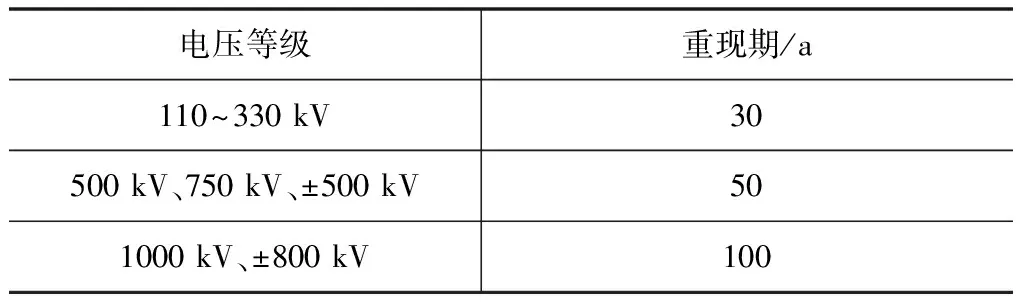
表1 我国架空输电线路覆冰厚度的重现期

1.2 导线覆冰厚度的确定

导线覆冰厚度是指覆冰成圆形的厚度，然而由于风力的影响，实际覆冰断面可能呈各种不规则形状。我国现行电力行业标准DL/T 5158-2012推荐输电线路设计覆冰荷载可以用单位长度设计覆冰质量G计算导线覆冰厚度B0，即

(2)

式中：L为导线覆冰长度(mm)；r为导线半径(mm)。

2 导线覆冰厚度的概率模型比较

2.1 概率分布拟合函数的选取

在确定某一重现期下的导线覆冰厚度时，采用不同的概率统计模型得到的结果可能差别甚大，同时由于地区地形、气候的差异，很难确定一个通用的概率模型进行极值分析。气象学上，对气候要素的极值进行拟合，常用正态分布函数、广义极值分布函数来拟合[10]。本文分别选取正态分布、极值Ⅰ型、极值Ⅱ型、极值Ⅲ型和PearsonⅢ型分布函数来对覆冰荷载进行拟合检验。

由中心极限定理知道：设X1，X2，…，Xn独立同分布的随机变量序列，且具有数学期望μ和方差σ。经标准化的随机变量设为Yn，其分布函数设为Fn(x)0，则:

(3)

当n充分大时，Yn收敛于标准正态分布，即:

(4)

由Fisher-Tippett极值类型定理知[11]：设X1，X2，…，Xn是独立同分布的随机变量序列，如果存在常数列{an>0}和{bn}，使得:

(5)

若式(5)成立，则式(5)中的非退化分布函数H(x)属于下列三种类型之一：

①极值Ⅰ型分布(Gumbel分布)：

(6)

②极值Ⅱ型分布(Fréchet分布)：

(7)

③极值Ⅲ型分布(Weibull分布)：

(8)

上述分布函数中：a为尺寸参数；b为位置参数；γ为形状参数。

PearsonⅢ型概率分布是Pearson曲线族中的一种线型，具有广泛的概括和模拟能力，在气象上常用来拟合年最大风速和最大日降雨量等极值分布[12]。DL/T 5158-2012规定，覆冰频率的计算概型也可采用Pearson型分布。PearsonⅢ型概率分布的概率密度函数和保证率分布函数分别为：

(9)

(10)

2.2 覆冰厚度概率分布模型拟合

根据本文目前收集到的年最大覆冰厚度，以确定拟合度较优的概率统计模型。湖北恩施绿葱坡观测站1959～1983年测得的年最大覆冰质量观测值以及计算的覆冰厚度详见附表1。捷克Studnice观测站1940～1999年测得的年最大覆冰质量观测值以及计算的覆冰厚度见附表2。

表2 湖北恩施绿葱坡和捷克Studnice观测站覆冰厚度的概率分布拟合函数

2.3 不同概率分布函数的拟合度检验

为便于比较，这里将实测覆冰厚度的累积分布与表2中两个观测站的概率分布拟合函数绘制在图1中。由图1可以看出，与实际覆冰厚度的概率分布相比，对恩施观测站1959～1983年间的年最大覆冰厚度拟合的5种分布函数均比较吻合，但极值Ⅱ型分布的偏差略微偏大一点；对捷克Studnice覆冰观测站1940～1999年间的年最大覆冰厚度拟合的5种分布函数中，除了正态分布外，其他四种分布函数均比较吻合。

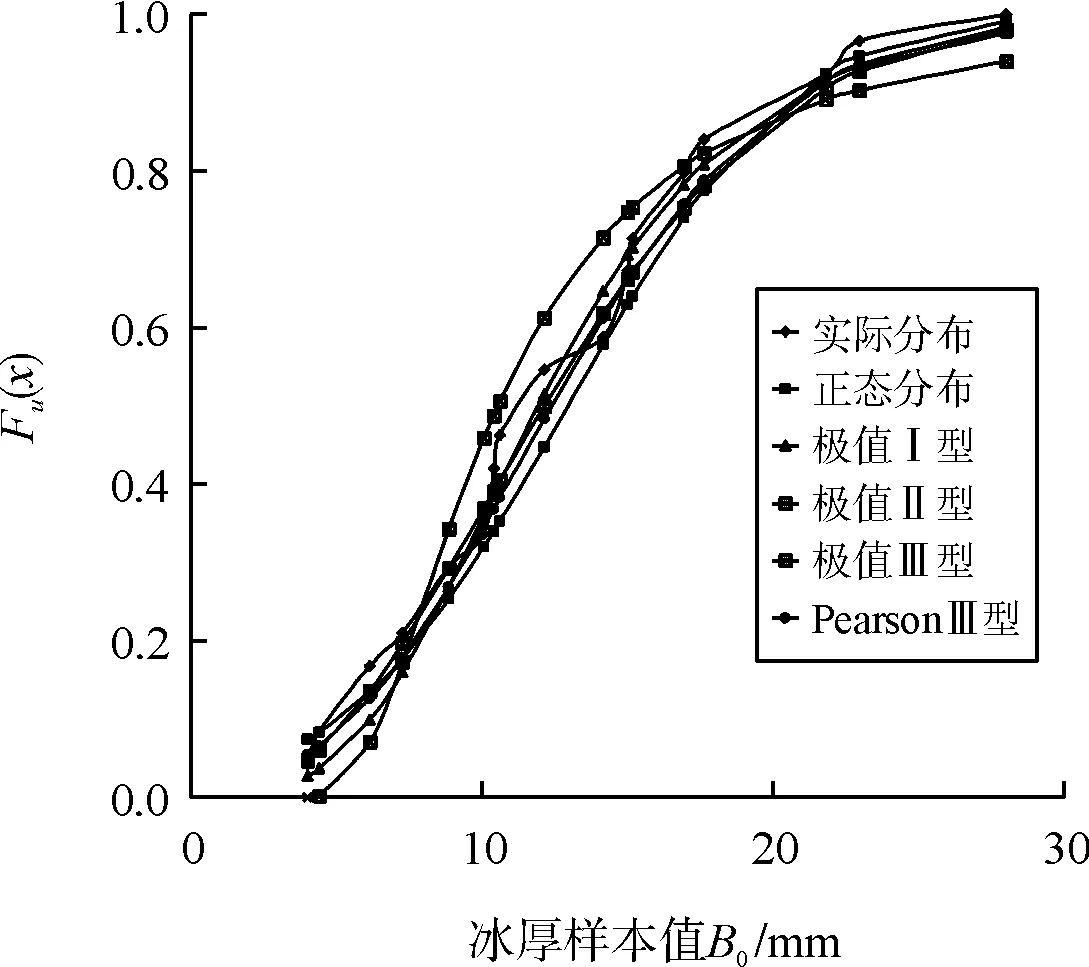
(a)恩施观测站

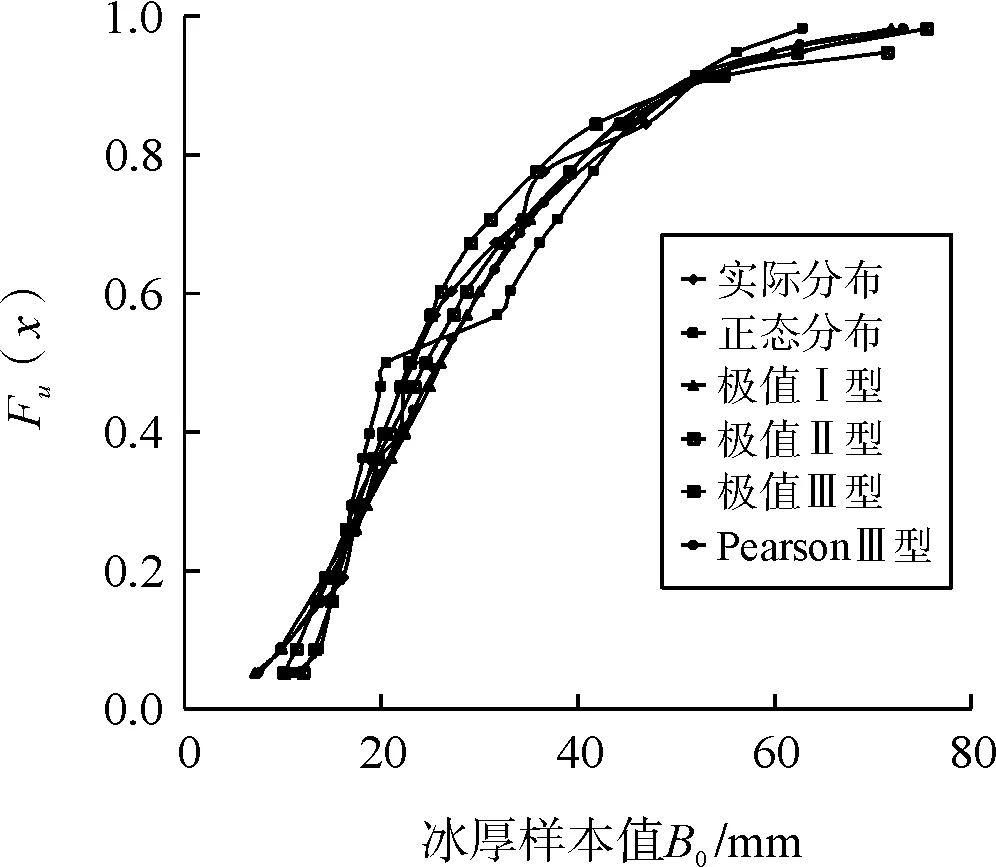
(b)捷克观测站图1 覆冰厚度不同概率分布拟合函数与实际覆冰概率分布的对比

为了进一步评判各种概率分布拟合函数的优劣，本文采用柯尔莫戈洛夫检验法对上述各种概率分布函数的拟合度进行了检验，结果见表3。

表3 覆冰厚度概率分布拟合函数的检验

由表3的计算结果可知，湖北恩施观测站的覆冰厚度均接受正态、极值Ⅰ型、极值Ⅱ型和极值Ⅲ型以及PearsonⅢ型分布。根据各种分布函数拟合的最大偏差可知，极值Ⅰ型分布函数与湖北恩施实际覆冰厚度分布的拟合度最优，极值Ⅲ型分布函数的拟合度次之，正态分布函数和极值Ⅱ型分布函数的拟合度较差。捷克Studnice观测站的覆冰厚度除不接受正态分布外，均可接受极值Ⅰ型、极值Ⅱ型和极值Ⅲ型以及PearsonⅢ型分布。其中，极值Ⅱ型分布函数与捷克Studnice实际覆冰厚度分布的拟合度最优，PearsonⅢ型、极值Ⅰ型和极值Ⅲ型分布函数拟合度均较好。由此可见，不同区域覆冰厚度的最优概率分布模型是有差异的，实际工程应用中，应结合当地的实际观测数据对概率分布模型进行筛选和调整。

2.4 不同重现期覆冰厚度的计算

根据输电线路覆冰厚度的概率分布函数及拟合度检验结果，按照不同概率分布函数的分布值Fu和重现期T之间的关系式(1)，即可求得不同重现期的覆冰厚度，结果见表4。由于捷克Studnice观测站的覆冰厚度不接受正态分布，表中未按正态分布计算该站在不同重现期的覆冰厚度。

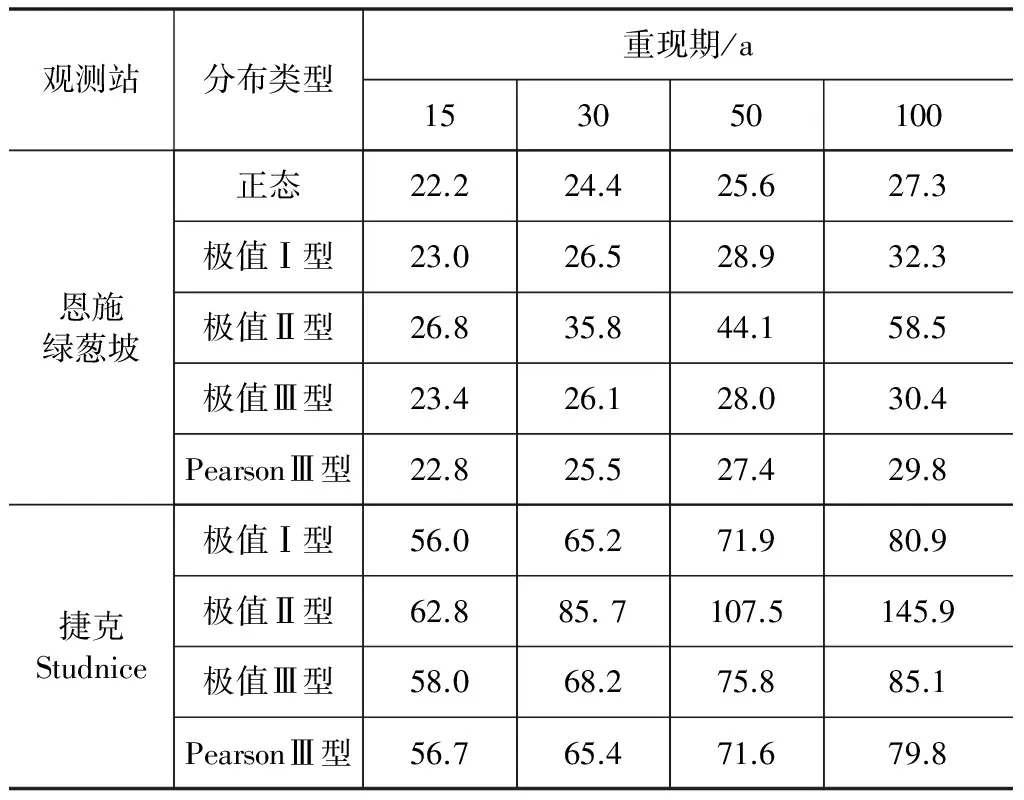
表4 按各概率分布函数计算的不同重现期覆冰厚度B mm

由表4可以看出，采用不同概率分布函数计算的同一重现期下覆冰厚度差别较大。以我国湖北恩施观测站的年最大覆冰厚度拟合的、且可接受的概率分布函数中，在同一重现期下，按极值Ⅱ型分布计算的覆冰厚度最大，按拟合度最优的极值Ⅰ型分布计算的覆冰厚度次之，按极值Ⅲ型分布计算的覆冰厚度与按极值Ⅰ型分布计算的结果非常相近，按正态分布计算的覆冰厚度最小。以捷克Studnice观测站的年最大覆冰厚度拟合的、且可接受的概率分布函数中，按拟合度最优的极值Ⅱ型分布计算的覆冰厚度最大，按极值Ⅲ型分布计算的覆冰厚度次之，按极值Ⅰ型分布和PearsonⅢ型分布计算的覆冰厚度最小。

3 主要结论

本文根据我国恩施绿葱坡和国外捷克Studnice覆冰观测站的年最大覆冰观测数据，对输电线路覆冰厚度的概率分布模型进行了拟合，并采用柯尔莫戈洛夫检验法对覆冰厚度的概率分布模型的进行了检验分析，主要结论如下：

(1)不同区域覆冰厚度的最优概率分布模型是有差异的。对于覆冰厚度较小的我国湖北恩施地区，其覆冰厚度以极值Ⅰ型分布函数的拟合度为最优，而对于覆冰厚度较大的捷克Studnice，其覆冰厚度以极值Ⅱ型分布函数的拟合度为最优。

(2)在同一重现期下，采用不同概率分布模型计算的覆冰厚度差别较大，其中以极值Ⅱ型分布模型计算的覆冰厚度为最大，而以正态分布模型计算的覆冰厚度为最小。根据覆冰厚度概率分布模型的拟合度检验结果和不同重现期覆冰厚度的计算结果，本文建议我国湖北恩施地区的覆冰厚度宜采用极值Ⅰ型分布函数拟合，当覆冰荷载重现期按50年考虑时，其覆冰厚度可取为29mm；当覆冰荷载重现期按100年考虑时，其覆冰厚度可取为33mm。

(3)根据覆冰厚度概率分布函数拟合度检验结果和不同重现期覆冰厚度的计算结果，本文建议对于覆冰厚度较小的普通覆冰区的输电线路，宜采用极值Ⅰ型概率分布函数确定输电线路覆冰厚度；对于重覆冰区的输电线路，或者缺少足够覆冰观测资料的地区，宜采用极值Ⅱ型概率分布函数确定输电线路覆冰厚度。

附表1 恩施观测站1959-1983年间年最大覆冰质量观测值及冰厚

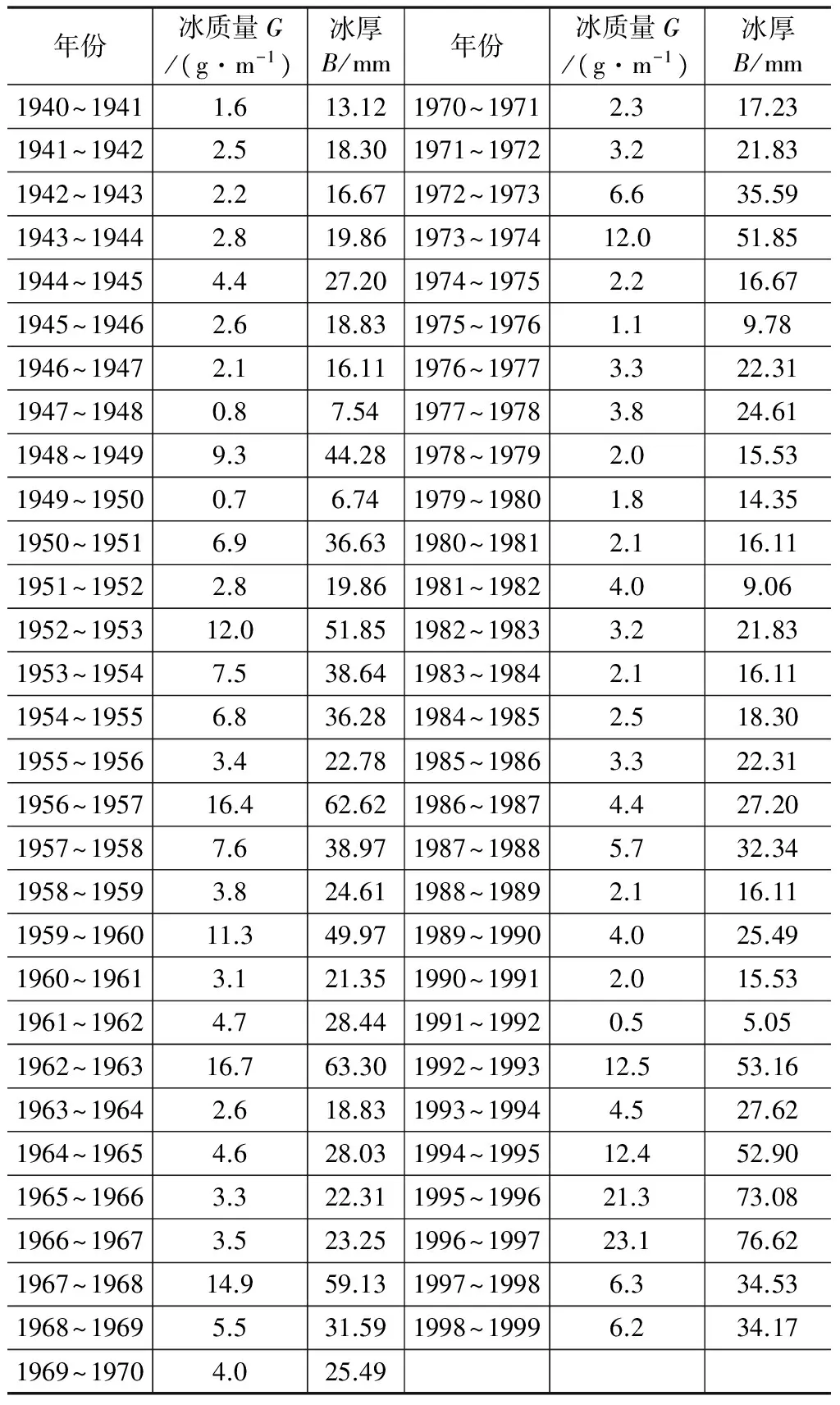
附表2 捷克Studnice观测站1940-1999年间年最大覆冰质量观测值及冰厚

[1] 徐文军，杨洪明，赵俊华，等. 冰风暴灾害下电力断线倒塔的概率计算[J]. 电力系统自动化, 2011, 35(1):13-17

[2] Xie Qiang, Zhu Ruiyuan．Damage to electric power grid infrastructure caused by natural disasters in China[J]．IEEE Power and Energy Magazine，2011,9(2):28-36

[3] DL/T5400-2009 重覆冰架空输电线路设计技术规程[S]

[4] International Electroteehnieal Commission．IEC60826(2003) Design Criteria of Overhead Transmission Lines[S]．Switzerland：HIS 2003

[5] DL/T 5158—2012 电力工程气象勘测技术规定[S]

[6] Canadian Standards Association.CAN/CSA—C22.3 NO.1—01 Overhead Systems[S].Canada：2003

[7] 蒋兴良,易辉.输电线路覆冰及防护[M].北京:中国电力出版社，2002

[8] 邹明华，邓洪洲.输电线路设计覆冰厚度统计模型取用[J].电网与清洁能源，2010,26(1)：40-44

[9] GB 50545-2010 110～750 kV架空输电线路设计技术规程[S]

[10] 屠其璞,王俊德,丁裕国.气象应用概率统计学[M].北京:气象出版社,1984

[11] Leadbetter M R,Lindgren G and Rootzen H Extreme and Related Properties of Random Sequences and Processes. New York:Spring-verlag,1983

[12] 高绍凤,陈万隆,朱超群,等.应用气候学[M]. 北京: 气象出版社, 2001

[13] 马开玉,张耀存.现代应用统计学[M].北京:中国气象出版社, 2004

[14] 张秀芝.概率权重矩法及其在Weibull分布参数估计中的应用[J]. 海洋预报， 1994,11(3);55-61

[15] 马开玉.三参数Weibull 分布参数估计的一种新方法[J].气象科学，1990,10(2):208-212

陆益锰(1989～)，男，硕士研究生，主要研究方向为结构可靠理论及应用。

TM752+.5

A

[定稿日期]2015-03-17