不同场地条件下曲线梁桥抗震性能研究

武兆驰

(中国中铁四局集团第二工程有限责任公司，江苏苏州 215131)

不同场地条件下曲线梁桥抗震性能研究

武兆驰

(中国中铁四局集团第二工程有限责任公司，江苏苏州 215131)

为了研究不同场地条件对曲线梁桥抗震性能的影响，依据美国NEHRP场地划分规则，按照谱兼容的原则选择符合不同场地类型的天然地震动，并以一座曲线连续梁桥为例，对其进行了地震作用下的动力弹塑性分析，完成了不同场地条件下曲线连续梁桥的抗震分析。研究结果表明：场地条件会对曲线梁桥结构的响应产生显著的影响，并且结构响应从A类场地到E类场地依次增加。因此在曲线梁桥的抗震设计中如果忽略场地条件带来的影响，将会过低地估计结构的响应。

桥梁工程； 曲线梁桥； 场地条件； 抗震分析

处于不同场地条件的建筑结构在同一次地震中往往会表现出不同程度的损伤，这是由于场地条件会对地震动的特性产生较大的影响。这些影响主要体现在对地震动的幅值和频谱特性的改变，具体表现为对地震动的放大和缩小，进而直接影响到建筑物的破坏程度[1-2]。在1906年美国发生旧金山大地震后，Wood[3]对震中区附近的震害进行了现场调查时发现不同场地条件上的建筑物差异十分明显，并且随后的全球强震记录以及震害调查资料都与Wood给出的结果相一致。这使得如何正确估计场地条件对工程结构的影响成为地震工程学的热点问题。对于桥梁在不同场地条件下的地震响应，各国学者已经进行了较为广泛的研究，如简支梁桥[4]、大跨桥梁[5]、钢管混凝土桥[6]、高墩桥[7-8]、斜拉桥[9]等。

1 工程概况

为了研究不同场地条件对曲线梁桥抗震性能的影响，本文以一座跨径布置为4×40 m、曲率半径为R=100 m的曲线连续混凝土梁桥为例。其主梁截面形式采用顶板宽12 m、底板宽7.5 m的单箱双室结构，外侧悬臂端板长为2.25 m，悬臂端部厚度为0.15 m，悬臂根部厚度为0.45 m；箱梁顶板厚0.25 m，箱梁端部厚度增至0.45 m，箱梁底板厚0.25 m，箱梁端部厚度增至0.45 m；梁高为2 m，腹板厚0.05 m；盖梁长度为10.7 m，横截面形式为1.6 m×1.7 m；在3#中间墩两圆柱形桥墩之间布设的横系梁尺寸为0.12 m×0.1 m×0.6 m；1#、2#、4#、5#桥墩直径为1.5 m，3#桥墩直径为2 m，均为圆形双柱墩；1#、5#桥墩墩高17 m，2#、4#桥墩墩高20 m，3#桥墩墩高25 m。主梁采用C40混凝土，盖梁和桥墩采用C30混凝土。各个盖梁顶面对称布置两个盆式橡胶支座，其中1#、2#、4#、5#墩布设顺桥向单向滑动支座，3#中间墩布设固定支座。图1为全桥整体布置图。

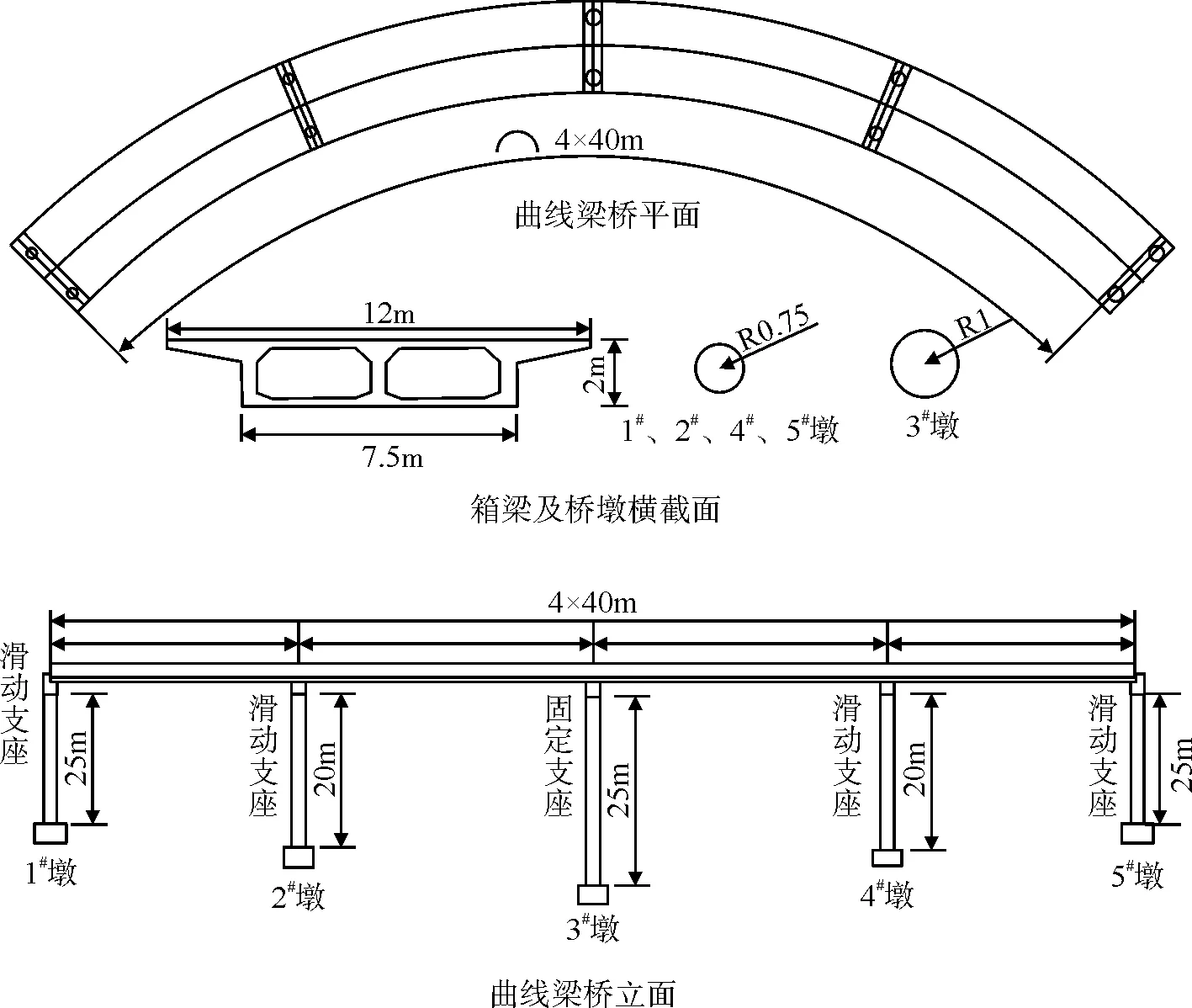
图1 全桥整体布置(单位：cm)

2 有限元模型建立

对于上述曲线梁桥结构，以Ansys有限元软件为平台，建立了全桥动力分析三维有限元模型。主梁、桥墩均采用每个节点具有6个自由度(3个平动和3个转动)的两节点梁单元(beam189)进行模拟。盆式橡胶支座采用双线性理想弹塑性弹簧单元(combin39)模拟,墩底处的支撑采用约束所有自由度的固定支撑。全桥有限元模型如图2所示。

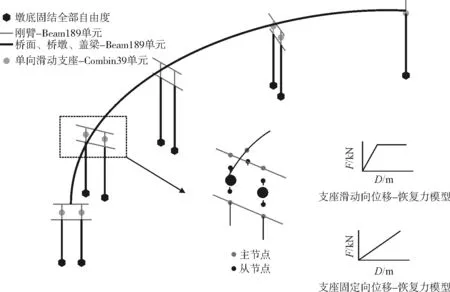
图2 全桥有限元模型(单位：cm)

对于1#、2#、4#及5#墩墩顶布置的单向滑动支座，按照桥梁抗震规范[10]采用双线性滞回模型进行模拟(图2)。支座的初始刚度按式(1)计算：

(1)

式中：μ为摩擦系数，依据支座试验结果取值为0.15；d为屈服位移，取值为0.0025；N为支座对上部结构的支反力。各支座详细参数如表1所示。

3 地震波的选取

对于场地效应的研究，依据美国NEHRP场地分类标准[11]来划分场地，并使用PEER-NGA谱模型[12]来生成目

表1 滑动支座等效模型的计算参数

标谱。这是因为PEER-NGA谱模型通过Vs30来确定场地分类，可以和NEHRP场地划分标准很好的相对应。为了使结果具有一般性，每种场地条件下均选择了3条符合要求的地震动时程记录，每条地震动分别沿X向、Y向及X+Y向进行输入，其中X向为两桥台连线方向，Y向为垂直于两桥台连线方向。此外，由于地震动均包含了两个方向的加速度时程，即FN(垂直于断层)向和FP(平行于断层)向，因此定义峰值较大的那个方向的加速度时程为主地震动时程，另外一个方向的加速度时程为次地震动时程。在进行单向输入时，分别沿X向和Y向输入，并且每个方向的输入均采用主加速度时程。而对于双向输入，将分为两种情形：在第一种情形中，X向采用主加速度时程，Y向采用次加速度时程，激励方向记为XY向激励；第二种情形反之，激励方向记为YX。所有工况如表2所示，图3给出了对应于各类场地的实际地震动加速度时程。

图3 不同场地条件下所选各地震动的加速度时程

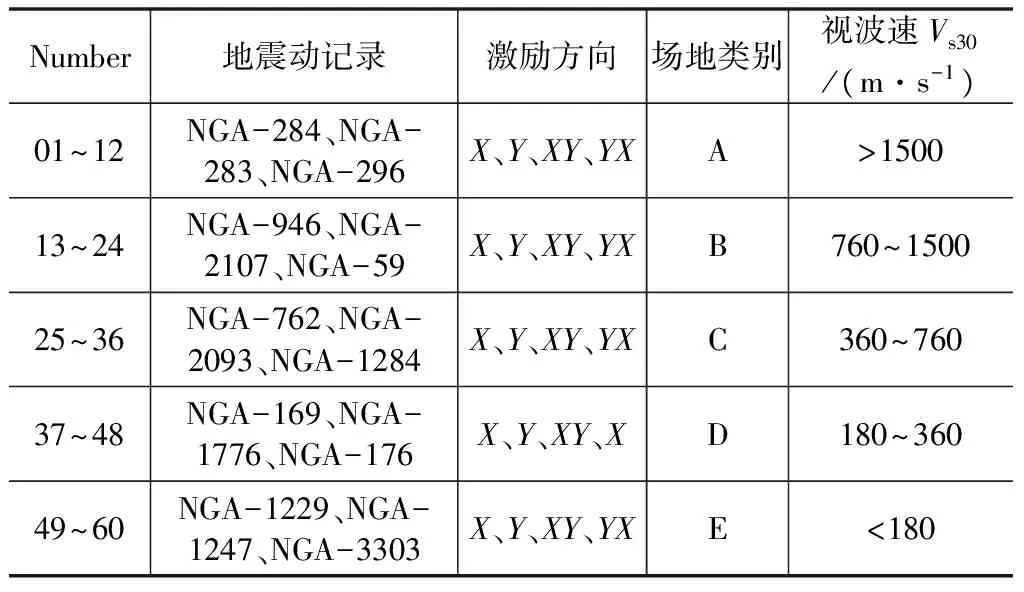
表2 对于场地效应研究的工况设置

4 计算结果分析

按照第3节所列出的工况，基于OPENSEES有限元平台采用弹塑性时程分析方法研究了场地效应对曲线梁桥结构抗震响应的影响。为了衡量在不同场地条件下地震作用所引起的加速度响应大小，本文采用了Arias强度即AI(Arias Intensity)来表示结构加速度响应的大小。AI是由Arias提出的以时域方法描述地震动潜在破坏趋势的一个参数[13]，其数学表达式为：

(2)

对于桥墩墩顶的加速度响应AI，本文以3#桥墩为例，图4、图5分别给出了在单向输入和双向输入下桥墩切向和径向加速度响应的AI。从图3可以看出场地条件从A变化到E，在单向激励下墩顶加速度响应的AI逐渐变大。从图4中也可以发现对于双向激励桥墩加速度响应的AI也有相同的规律。此外还可以发现，相对于A类场地，E类场地对墩顶加速度响应的放大作用最为明显。从图4中可以看出，对于切向响应，主方向为Y向时对桥墩加速度响应的放大作用更为明显；而对于径向响应，当主方向为X向时对桥墩加速度响应的放大作用更为明显。

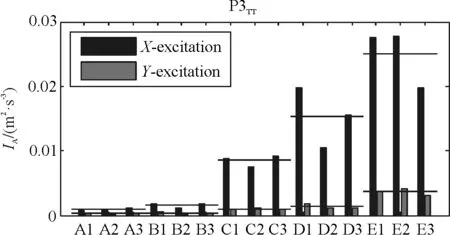
(a)切向响应

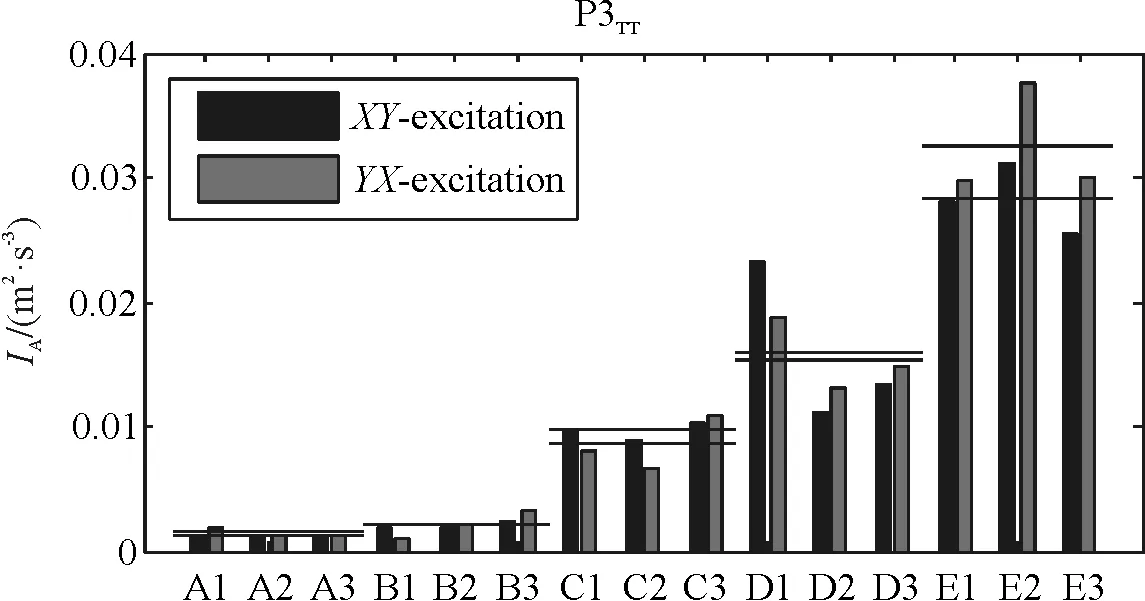
(a)切向响应

(b)径向响应图5 双向输入下墩顶加速度响应AI

图6、图7给出了桥梁结构在不同场地条件下受单向激励和双向激励时的桥墩相对位移。从图5可以看出，在单向激励下桥墩的相对位移从A类场地到E类场地依次增大。从图6也可以看出在双向激励下，桥墩相对位移从A类场地到E类场地依次增大。同时还可以发现，曲线梁桥在C类场地和D类场地条件下的桥墩相对位移比较接近。

图8给出了在单向激励和双向激励下不同场地条件的支座位移。从图7中可以看出，与墩顶加速度响应AI和桥墩相对位移类似，支座变形也从A类场地到E类场地依次增大。场地条件对支座位移、墩顶加速度以及桥墩变形均产生了显著影响。

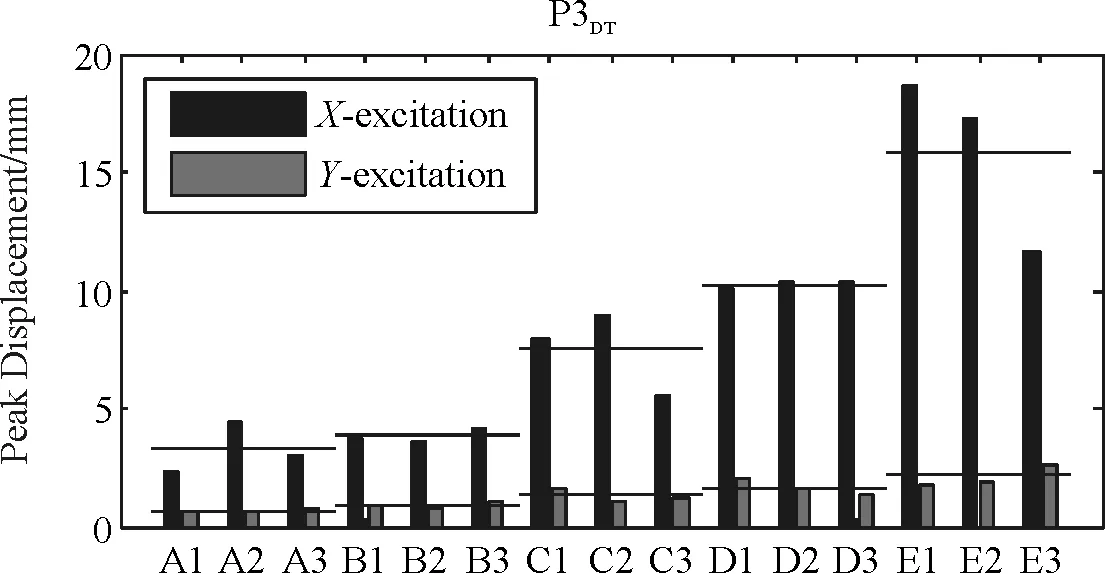
(a)切向响应

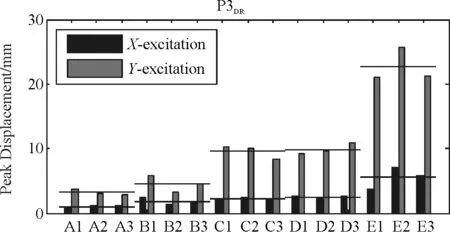
(b)径向响应图6 单向输入下桥墩相对位移

(a)切向响应

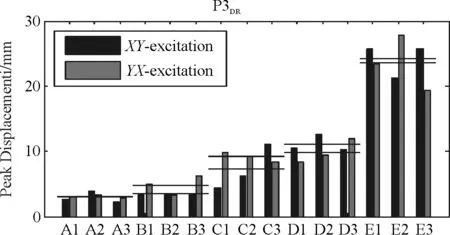
(b)径向响应图7 双向输入下桥墩相对位移

5 结论

本文基于一座典型的曲线梁桥，研究了不同场地条件对其地震响应的影响。针对每种场地条件均选择了3条实际地震记录，并进行了动力弹塑性分析，对比了曲线梁桥在不同场地条件下的地震响应，可以得出以下结论：

(1)场地条件对曲线梁桥的墩顶加速度响应、桥墩相对位移以及支座变形均产生了明显的影响。并且结构响应从A类场地到E类场地依次增大；

(2)场地条件会引起结构响应产生显著的变化，如果在曲线梁桥的抗震设计中不考虑场地条件的影响，将会低估结构的响应。

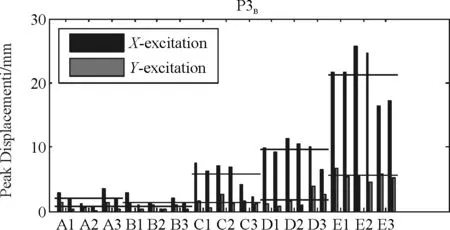
(a)单向输入

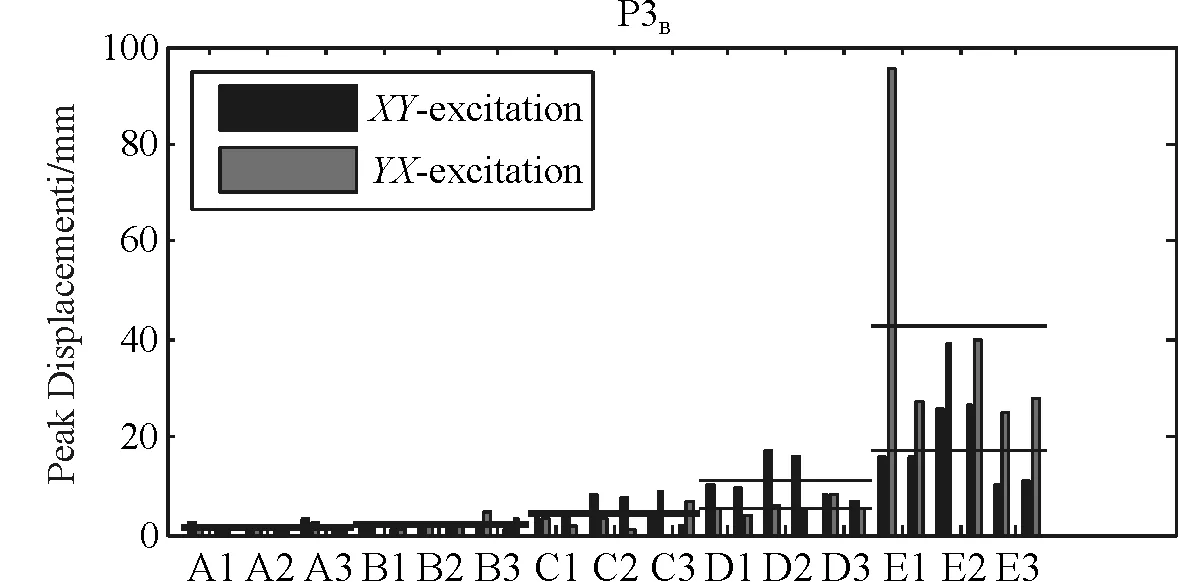
(b)双向输入图8 支座位移

[1] 胡聿贤, 孙平善, 章在墉, 等. 场地条件对震害和地震动的影响[J]. 地震工程与工程振动, 1980, 1 (1): 41-54

[2] 薄景山, 李秀领, 李山有. 场地条件对地震动影响研究的若干进展[J]. 世界地震工程, 2003, 19(2): 11-15

[3] Richter C F. Elementary Seismology[M]. San-Francisco, 1958

[4] 于海龙. 地震作用下简支梁桥梁间碰撞响应分析[D]. 北京交通大学, 2004

[5] 臧明明，陈清军. 长周期地震动的场地效应与大跨桥梁结构的动力响应分析[J]. 结构工程师， 2010，(1): 118-125

[6] 闫维明，李晰，陈彦江，等. 钢管混凝土拱桥台阵试验研究:场地条件的影响[J]. 工程力学， 2013，(6): 116-123

[7] 贾宏宇，郑史雄. 基于场地效应的山区高墩桥梁随机地震响应分析[J]. 公路交通科技， 2012，(6): 93-97

[8] 贾宏宇，张克跃，郑史雄，等. 空间变化场地对超高墩铁路桥梁地震响应的影响[J]. 公路交通科技， 2014，(9): 43-49

[9] 范立础，王君杰，陈玮. 非一致地震激励下大跨度斜拉桥的响应特征[J]. 计算力学学报， 2001，(3): 358-363

[10] JTG/TB 02-01-2008 公路桥梁抗震设计细则 [S]

[11] Fema. Earthquake-Resistant Design Concepts: An Introduction to the NEHRP Recommended Seismic Provisions for New Buildings and Other Structures[S]. 2010

[12] Peer. Technical report for the PEER ground motion database web application[R]. Pacific Earthquake Engineering Research Center, 2010

[13] Arias A. A measure of earthquake intensity [M].Seismic Design of Nuclear Power Plants. MIT Press

武兆驰(1978～)，男，工程师，主要研究方向：桥梁施工及结构空间行为。

U442.5+5

A

[定稿日期]2014-11-07