导线对地电容对牵引供电仿真的影响分析

陈梦琪，李华伟，陈富伟，李善颖，曹天植，吴 涛

导线对地电容对牵引供电仿真的影响分析

陈梦琪，李华伟，陈富伟，李善颖，曹天植，吴 涛

为定量分析导线对地电容对牵引供电仿真的影响，通过MATLAB/SIMULINK建立具体仿真算例，说明了部分电容对牵引网电压电流的影响。最后定量给出了电容对牵引供电系统仿真计算的影响，为工程计算提供了更准确的依据。

牵引供电系统；镜像法；对地电容；仿真模型

0 引言

电气化铁路是一种特殊的大功率单相负荷，具有牵引功率大、波动大、非线性、冲击性和不对称性等特点，这就造成了电力系统三相的严重不平衡。国内外的研究学者在牵引供电系统的阻抗参数计算[1～3]、牵引网的数学模型建立[4～6]、牵引网暂稳态仿真[7～11]等方面做了大量的研究工作，而对多导线系统对地电容的影响没有做定量分析。

本文通过Carson公式计算线路参数，最后利用MATLAB/SIMULINK建立考虑导线对地电容与不考虑导线对地电容的牵引网仿真模型，定性并定量分析了导线对地电容对牵引供电系统的影响，为工程计算提供了更加准确的依据。

1 牵引网稳态仿真分析

仿真实验以单链形直接供电方式的牵引供电系统为例，各导线位置关系如图1所示。结构参数：接触网悬挂形式为单链形，接触导线rT= 0.184 Ω/km，Rεt= 8.57 mm；承力索GJ-70， rM= 2.0 Ω/km，χNm= 0.88 Ω/km，RM= 5.75 mm，接触线距轨面平均高度H = 5 800 mm，接触网结构高度h = 1 300 mm，承力索弛度fc= 600 mm，钢轨型号P50，rg= 0.18 Ω/km，χNg= 0.18 Ω/km，单根钢轨的等效半径Rεg= 5.54 mm，轨距dg= 1 435 mm，钢轨长度25 m；大地电导率σ = 10-4Ω/cm。

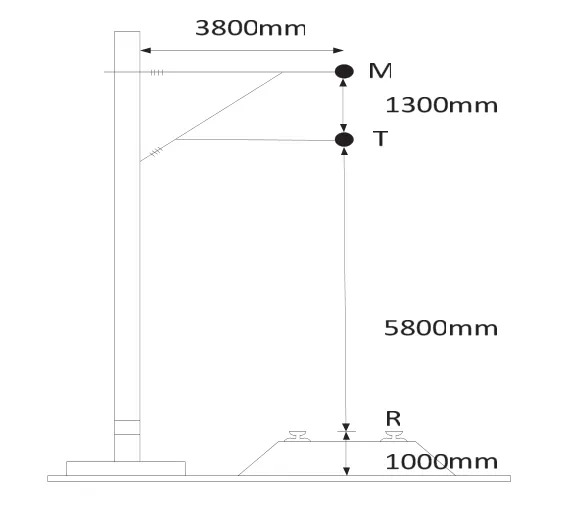
图1 牵引网悬挂系统示意图

在不影响研究对象电气量特性的前提下，对导体进行化简等效。承力索与接触线相互并联，在任意长度的分段中，导线间的电流分布不变，而且它们之间的相互位置关系较复杂，故将二者等效为一根平行于钢轨的导体1，将两对称分布的钢轨等效为单根导体2。各导体单位自阻抗与互阻抗数值如下：

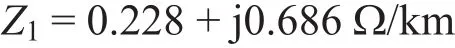
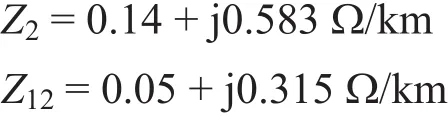
整个系统是由导体1、导体2和大地组成的独立系统，根据上述公式计算线路对地电容。在两供电臂设置不同的参数，得到正常运行工况下，列车距离变电所15 km时，牵引网仿真结果数据见表1，30 km时线路电流、电压波形如图2—图5所示。

表1 直接供电方式下网压分布及电流值表

列车位于距离变电所15 km处时，不考虑导体对地电容的线路电流各处相等，两线路电流幅值最大相对误差为0.03%。两线路电压相角相差0.01°，机车所在处幅值相对误差最大，为0.03%。

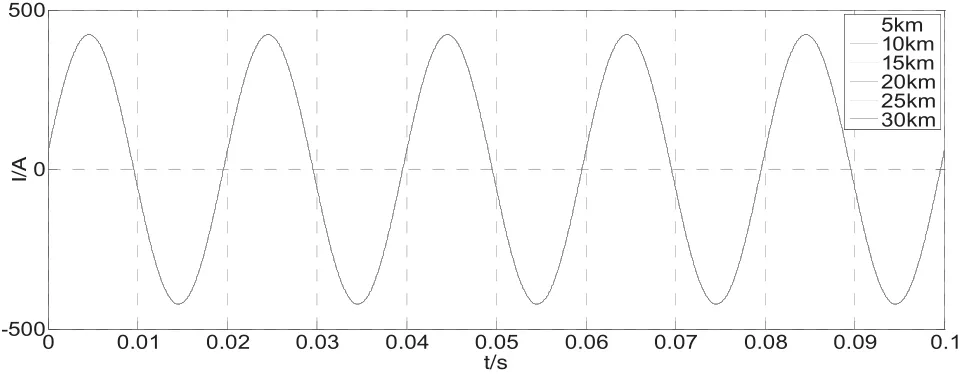
图2 不考虑导体对地电容时线路电流曲线图

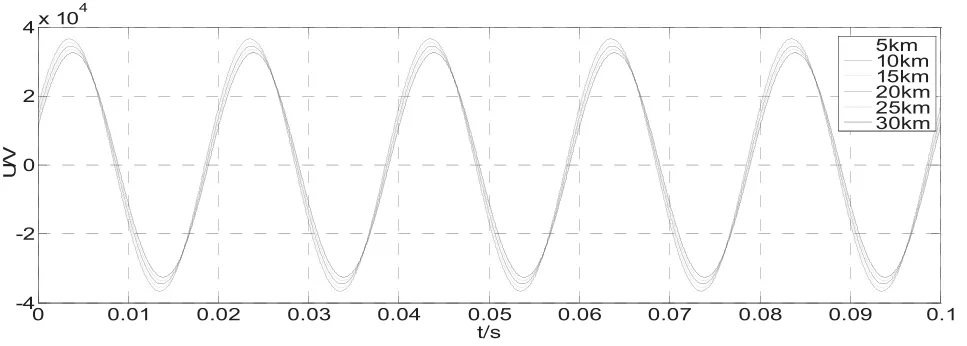
图3 不考虑导体对地电容时线路电压曲线图

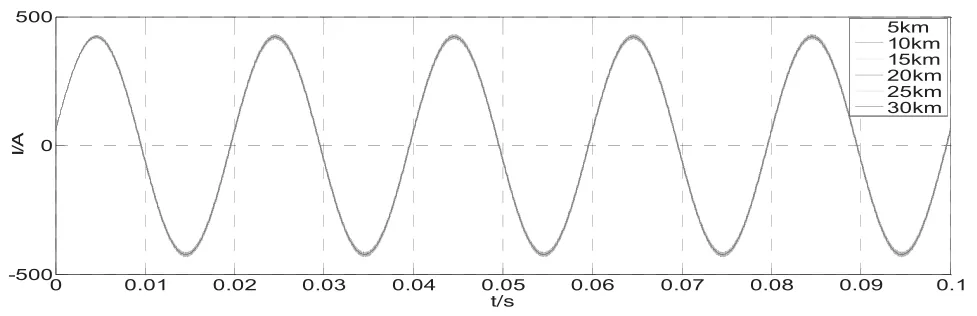
图4 考虑导体对地电容时线路电流曲线图

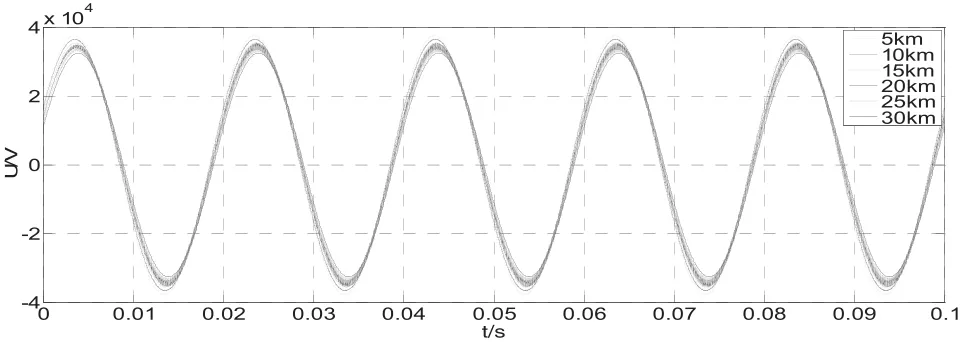
图5 考虑导体对地电容时线路电压曲线图

列车位于距离变电所30 km处时，两线路电流幅值最大相对误差为0.043%，相位差随距离的增长而缩小，且机车所在处考虑导体对地电容的线路电流滞后于不考虑导体对地电容的线路。机车所在处电压幅值相对误差最大，为0.042%。

2 牵引网暂态仿真

列车运行在距离变电所30 km处，此时在距离变电所20 km处设置断路器。断路器在0.02 s时刻断开，在0.06 s时重新闭合，使得线路在0.02 s出现断路故障，0.06 s故障切除。两线路电压电流仿真结果如图6和图7所示。

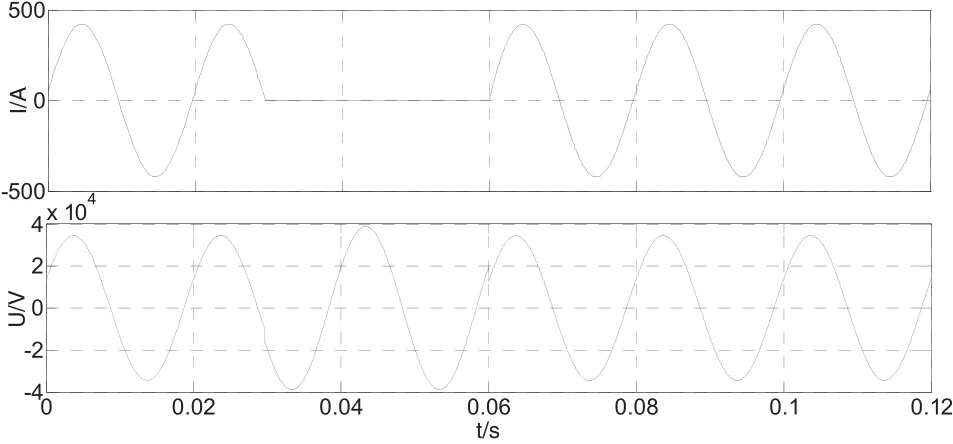
图6 断路故障时不考虑导体对地电容时线路电流电压波形图

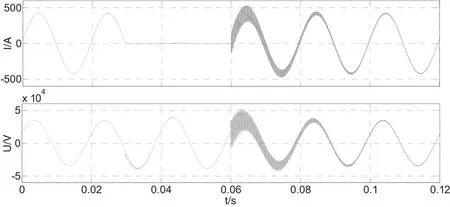
图7 断路故障时考虑导体对地电容时线路电流电压波形图

观察图6及图7可知，当线路切除故障后，考虑导体对地电容的线路会出现暂时过电压现象，然后较平稳的恢复稳态，更符合牵引网的真实运行特性[15]。

对比列车处于15 km与30 km时电压电流波形可知，不考虑导体对地电容的线路A，其电压电流曲线均为较光滑曲线，考虑导体对地电容的线路B，其曲线的整体变化趋势与线路A一致，是一条有波动的非平滑曲线，且距离变电所5 km处，电压电流曲线波动最明显，机车所在处电压最低。机车所在处电压电流曲线最为平滑，两线路电压幅值相对误差最大；且列车距离变电所越远，导体对地电容对线路的影响越大。

综上可知，在本文所建模型及参数设置下，系统发生故障及切除故障后对系统的电压电流影响不大，符合牵引网的暂稳态电气特性。为准确分析牵引供电系统的真实运行情况，综合考虑导体对地电容的影响，具有可行性，且更加符合牵引网的电气性能。

3 结论

线路参数是电力系统分析所必需的一项基本数据，实际工程中，工程设计的线路参数全面性与准确性直接关系到整个供电系统的成败。

本文基于MATLAB/SIMULINK仿真工具，同时建立考虑导体对地电容及不考虑导体对地电容的牵引网仿真模型，定量分析了2种情况下的相对误差，得出列车所在处电压误差最大；随着列车距离变电所越远，导体对地电容对线路电压和电流的影响越大。论文主要进行了较详细的仿真计算，定量给出了电容对铁路供电系统仿真计算的影响，虽然误差很小，在工程计算中可以忽略不计，但是这个定量的分析，为工程计算提供了更准确的依据。

[1] 何正友，胡海涛，方雷，等.高速铁路牵引供电系统谐波及其传输特性研究[J].中国电机工程学报，2011，31（16）：55-62.

[2] 姚楠．电气化铁道牵引网基波与谐波模型研究[D]．北京：北京交通大学，2008．

[3] 李群湛.牵引变电所电气量的通用变换方法及其应用[J].铁道学报，1994，16（1）：17-23.

[4] 郎兵，吴命利.牵引网谐波模型及其仿真计算[J].电力系统自动化，2009，33（17）：76-80.

[5] 何俊文．牵引供电系统负荷过程仿真[D]．成都：西南交通大学，2010．

[6] 吴命利．牵引供电系统电气参数与数学模型研究[D]．北京：北京交通大学，2006．

[7] 张杨，刘志刚．基于电磁暂态分析的高速铁路牵引网谐波模型及谐波特性分析[J]．电网技术，2011，35（5）：70-75.

[8] 邢晓乾．带加强线的全并联直接供电技术的研究[D]．成都：西南交通大学，2011．

[9] 王奇，刘志刚，白玮莉，等．基于PSCAD/EMTDC的牵引供电系统仿真模型研究[J]．电力系统保护与控制，2009，37（16）：35-40.

[10] 李群湛，郭锴，周福林．交流电气化铁路AT供电牵引网电气分析[J]．西南交通大学学报，2012，47（1）：1-6.

[11] Hanmin Lee, Changmu Lee, GilsooIang. Harmonic analysis of the Korean high-speed railway using the eight-port representation model [J]. IEEE Transactions on Power Delivery, 2006, 21(2)：979-986．

[12] 冯慈璋，马西奎．工程电磁场导论[M]．北京：高等教育出版社，2008．

[13] 潘卫国．电气化铁道牵引网地面开关式自动过分相装置暂态过程分析[D]．成都：西南交通大学硕士学位论文，2008．

[14] 李群湛，贺建闵．牵引供电系统分析（第2版）[M]．成都：西南交通大学出版社，2010．

[15] 张瑞．电气化铁路暂态电气特性仿真研究[D]．成都：西南交通大学硕士学位论文，2009．

For quantitative analysis of impact of grounding capacitance on the traction power supply system, in this paper, MATLAB/SIMULINK is adopted to establish the specific simulation example. Based on this model, the traction network current and voltage distribution influenced bypartial capacitanceis simulated. At last, the influence of grounding capacitance on the traction power supply system is given quantitatively to provide the more accurate basis for engineering calculation.

Traction power supply system; method of images; ground capacitance; simulation model

U223.5

B

1007-936X(2015)01-0026-03

2014-07-18

陈梦琪.北京交通大学电气工程学院，硕士研究生，电话：010-51682436；李华伟，陈富伟.北京交通大学电气工程学院；李善颖，曹天植，吴 涛.华北电力科学研究院有限责任公司。