基于GPS和BDS组合精密单点定位精度分析
张震
(福州市勘测院,福建 福州 350108)
1 引 言
北斗卫星导航系统简称北斗系统,英文缩写为BDS,其空间星座由5 颗地球静止轨道(GEO)卫星、27颗中圆地球轨道(MEO)卫星和3 颗倾斜地球同步轨道(IGSO)卫星组成。截止到2012年底,在轨工作卫星有5 GEO、4 MEO 和5 IGSO[1]。北斗系统于2012年底开始向亚太地区提供定位、导航、授时等服务[1]。YANG 等分析了BDS 公众用户的可视卫星数以及其几何精度值(DOP)[2]。Shi 等利用武汉大学GNSS 中心提供的精密星历和精密钟差产品解算得到BDS 静态PPP 达到cm 级,动态RTK 可以达到5 cm~10 cm[3]。Li 等分析了GPS 单系统、BDS 单系统、GPS与BDS 组合系统三种定位模式,使用3 个站2 天的观测数据进行实验,得出GPS 与BDS 组合定位系统的收敛时间相比单系统明显减少,而在单系统本身卫星星座分布良好时,组合定位系统定位精度提高不大[4]。为了研究在现有星座条件下的BDS 定位性能,分别进行了GPS、BDS 和二者组合定位的实验。本文通过获取时间间隔10 s为期3 h的连续静态GPS 和BDS 观测实验数据,分别解算了BDS 和GPS 静态精密单点定位结果。同时,对时间间隔0.1 s为期1 h的车载GPS 和BDS 连续动态观测数据进行解算实验。通过改正了对流层延迟误差、相对论误差和地球自转等误差的影响,得到了BDS 和GPS 每个历元下的测站坐标,并对实验结果进行了分析。
2 原理
2.1 非差PPP 技术方法
无电离层组合观测方程为:

式中,P(Li)为Li 的伪距观测量;Φ(Li)为Li 载波相位观测量;ρ 为站星的几何距离;dtr、dts分别表示接收机与卫星钟差;c 为光速;△dtrop为对流层延迟量;λ为波长;N 为整周模糊度;M 为多路径效应影响;εP(L1+L2)、εΦ(L1+L2)分别表示伪距与载波相位的多路径效应和观测噪声。
假设在历元k,测站r 同时观测到m 颗卫星,则可以得到如下方程:
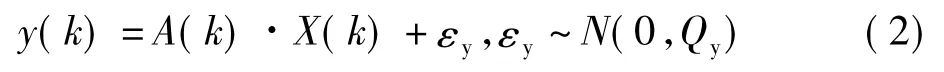
式中,y(k)为无电离层组合模型的码、相位观测值的观测值与计算值的差值,A(k)为系数矩阵,X(k)为未知数参量,包括测站坐标、接收机钟差、对流层延迟和无电离层组合的模糊度,εy为无电离层组合的观测噪声。
经线性化后,观测值与未知量之间只存在线性关系,可以采用Kalman 滤波来估计未知量。标准的Kalman 滤波形式如下[5]:
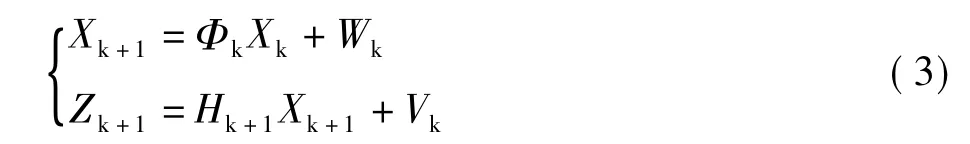
式中,X 为状态量;Z 为观测量;Φ 为状态转移矩阵;H 为设计矩阵;W 为过程噪声;V 为观测噪声;k 为历元数。
2.2 误差改正
从GNSS 接收机中得到的伪距和相位观测量中包含各种误差,可以将之分为三类:与卫星有关的误差,与传播路径有关的误差和与接收机有关的误差[6]。
对于与卫星有关的误差,主要包括卫星天线相位中心偏差、卫星硬件延迟、卫星轨道误差及其钟差等。卫星天线相位中心偏差主要采用IGS 发布的天线相位偏心参数表进行改正,硬件延迟偏差是由IGS 成立的专门工作组 BCWG(Bias and Calibration Working Group)长期的连续监测得到的经验值,并每月发布一次[7,8]。卫星轨道误差主要来源于插值影响,高阶拉格朗日内插能够满足轨道的精度要求。
与传播路径有关的误差主要有大气延迟引起的对流层误差。对流层延迟通常采用Hopfiled 模型或Saastamoine 模型进行改正[9],这两种对流层改正模型在低纬度改正效果相当;地球自转效应和相对论误差也可以通过相应的数学公式进行改正[9]。
对流层折射与地面气候大气压力湿度和温度变化密切相关,这比电离层延迟要更为复杂,不同对流层模型之间的差异不是很大[9]。本文采用Saastamoine 模型改正对流层延迟,此处对GPS 静态数据进行对流层改正,效果如图1 所示,左图为平面(N E 方向)改正效果,右图为高程方向改正效果。
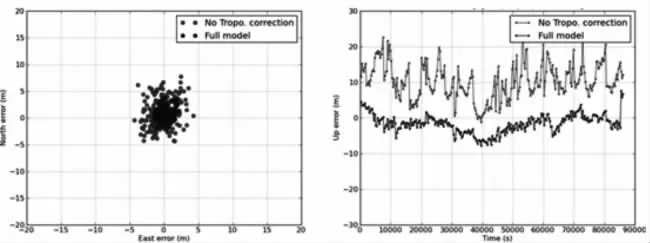
图1 对流层延迟的影响
与接收机有关的误差主要有接收机天线相位中心偏差,地球形变等。后者主要包括固体潮、海洋潮和极潮,它们都有相应的改正模型,详细可见[7]。
3 结果与分析
3.1 实验数据
静态实验数据来源于2014年7月31日广州地区,接收机采用的是司南导航的K508 板卡(如图2 所示),能够同时采集GPS、BDS 和GLONASS 三类卫星的观测和数据,本文暂不考虑GLONASS 卫星数据。动态数据来源于武汉地区,同样采用的司南K508 板卡,具体细节如表1 所示。

图2 司南K508 板卡
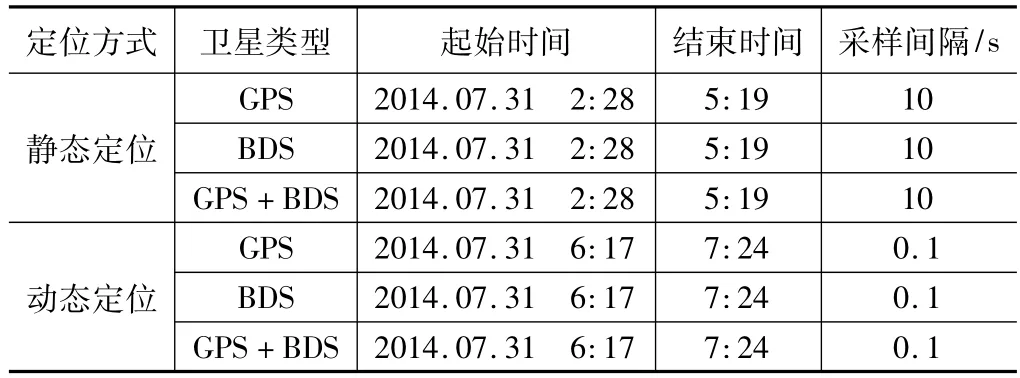
实验数据说明 表1
3.2 静态实验
统计GPS 和BDS 静态观测数据的可视卫星颗数,将该结果统计在表2,从表中可以看出静态GPS 可视卫星颗数最大值13,最小值7,平均值10.9;静态BDS可视卫星颗数最大值10,最小值8,平均值9.3,总体BDS 卫星颗数少于GPS;二者组合情况可视卫星颗数最高,达到19,均值为16.1。并分析DOP、PDOP、HDOP 和VDOP 值,结果如图3 所示。

统计可视卫星颗数 表2
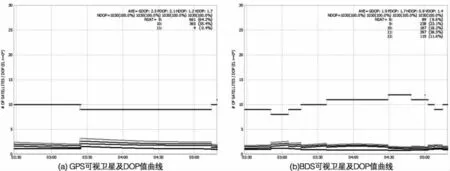
图3 静态实验可视卫星数及DOP 值曲线图
将GPS 和BDS 静态数据进行精密单点定位,分别绘制GPS、BDS 和二者组合定位的NEU 三个方向误差图,如图4 所示。
统计三种定位方案的XYZ 方向的定位精度,结果如表3 所示。从表3 可以看出,GPS 静态PPP 定位精度在XYZ 三方向的均值分别为4.36 cm、-3.17 cm和 2.19 cm;BDS 静态 PPP 定位精度分别为-7.86 cm、6.91 cm和9.89 cm,总体精度低于GPS;二者组合定位精度最高,三方向的均值分别为1.06 cm、0.97 cm和1.23 cm。

图4 NEU 方向定位曲线图
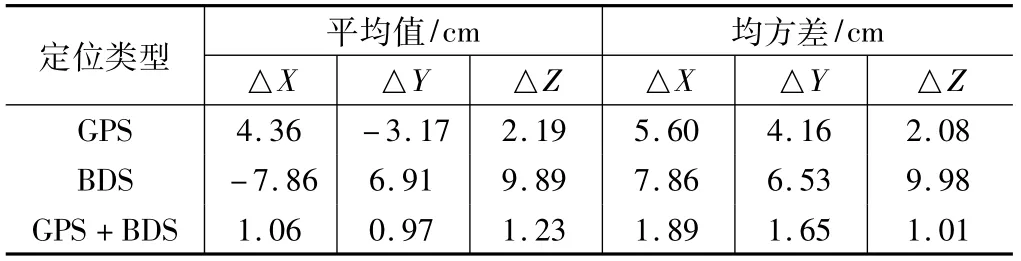
统计三种方案XYZ 定位精度 表3
3.3 动态实验
车载动态实验数据来源于武汉郊区,中间出现几处卫星颗数较少,导致DOP 值很大,主要是由周边高建筑、树木遮挡导致的。图5 分别绘制了GPS、BDS 和二者组合定位的可视卫星颗数及DOP 值。表4 统计了三种定位方案的可视卫星颗数情况,从中可以得出动态GPS 可视卫星颗数最大值为11,最小值为4,平均值为7.6;动态BDS 可视卫星可视最大值为8,最小值为4,均值为5.2,可见BDS 可视卫星颗数少于GPS。二者组合定位可视卫星颗数最多,卫星颗数处于6~16 之间,平均值为10.9。

图5 动态实验可视卫星数及DOP 曲线图
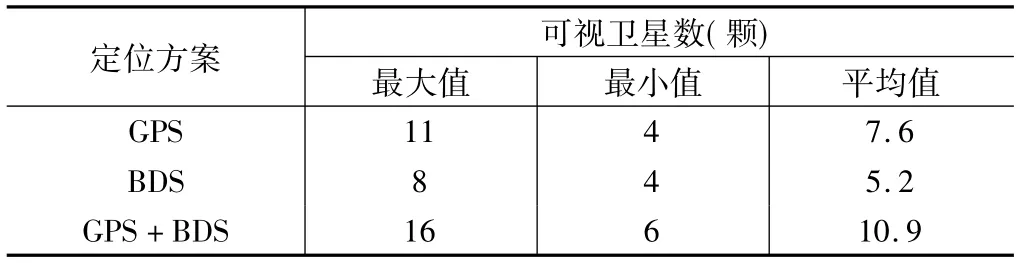
统计可视卫星颗数 表4
对于三类定位方案,分别绘制了车载接收机的轨迹图,如图6 所示。从图中可以看出车载GPS 动态定位效果良好,整个轨迹图符合实际车辆驾驶路径。车载BDS 动态定位性能一般,其中有几段出现结果为空,主要是受限于BDS 可视卫星低于4 颗的影响,总体来说动态BDS 精密定位可用于精度要求不高的导航应用。最后,组合定位的效果最优,可以看到整体轨迹最佳,尤其是在出现单GPS 或BDS 出现信号遮挡的情况,组合定位即可发挥重要的作用。
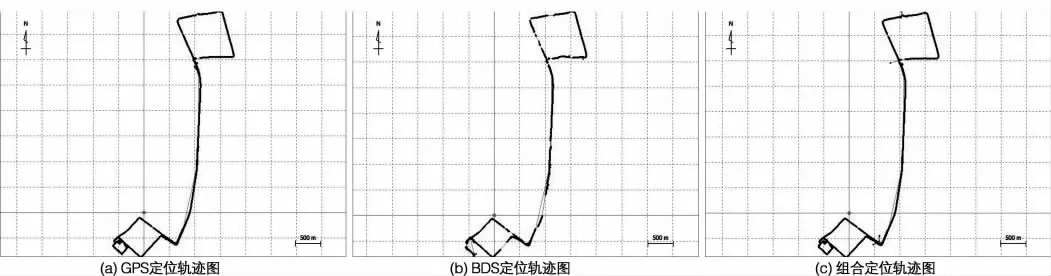
图6 车载接收机轨迹图
4 结 论
因北斗卫星导航系统已正式向亚太地区进行导航、定位、授时服务,利用静态GPS 和BDS 实际观测数据与车载GPS 和BDS 动态观测数据进行实验以及对实验结果进行分析显得尤为重要。同时,将GPS、BDS和二者组合定位解算结果进行比较,从本文可以得到以下结论:
(1)从静态GPS 和BDS 观测数据可以得出,BDS 可视卫星平均数为9.3,GPS 可视卫星平均颗数10.9,二者组合定位的可视卫星颗数最多,平均颗数为16.1。动态车载实验的可视卫星颗数同样反映这一规律。
(2)静态GPS 精密单点定位N、E 与U 三个方向的定位精度分别为4.36 cm、-3.17 cm和2.19 cm,定位精度较好。而静态BDS 精密单点定位N、E 与U三个方向的定位精度分别为-7.86 cm、6.91 cm和9.89 cm,定位精度次于GPS。
(3)车载GPS 和BDS 精密单点定位实验可以看出GPS 定位精度较好,BDS 次之,BDS 解算定位轨迹与GPS 整体一致。二者组合定位效果最优,尤其是在单GPS 或BDS 可是卫星只有4 的情况下,组合定位仍然可达7 颗,这对于精密单位定位尤为重要。
[1]中国卫星导航系统管理办公室.北斗卫星导航系统空间信号接口控制文件公开服务信号B1(2.0 版)[R].2013.
[2]Yang Y X,Li J L,Xu J Y,et al.Contribution of the Compass satellite navigation system to global PNT users[J].Chinese Science Bulletin,2011,Bull 56(26):2813~2819.
[3]Shi C,Zhao Q L,Li M,et al.Precise orbit determination of Beidou satellites with precise positioning[J].Science China Earth Sciences,2012,55(7):1079~1086.
[4]Li W,Teunissen P J G,Zhang B,et al.Precise point positioning using GPS and Compass observations[A].Proceedings of the 4th China satellite navigation conference(CSNC),Wuhan,China,2013:15~17.
[5]Han.S.Quality-control issues relating to instantaneous ambiguity resolution for real-time GPS kinematic positioning[J].Journal of Geodesy,1997,71(7):351~361.
[6]Kouba J,P.Héroux.GPS Precise Point Positioning Using IGS Orbit Products[J].GPS Solutions,2000,5(2).
[7]Abdel-salam M.Precise Point Positioning Using Un-Differenced Code and Carrier Phase Observations[D].Calgary:University of Calgary,2005.
[8]阮仁贵.GPS 非差相位精密单点定位研究[D].郑州:信息工程大学测绘学院,2009.
[9]何海波.高精度GPS 动态测量及质量控制[D].郑州:信息工程大学测绘学院,2002.

