物种敏感度分布的非参数核密度估计模型

王颖，冯承莲，黄文贤，刘跃丹，马燕,5，张瑞卿，吴丰昌,*

1. 北京师范大学水科学研究院，北京 100875 2. 中国环境科学研究院 环境基准与风险评估国家重点实验室，北京100012 3. 北京师范大学数学科学学院，北京 100875 4. 环境保护部华南环境科学研究所 广东省水与大气污染防治重点实验室，广州510065 5. 青岛理工大学环境与市政工程学院 生物环保与绿色化工研究中心，青岛266033 6. 内蒙古大学环境与资源学院，呼和浩特010021

物种敏感度分布的非参数核密度估计模型

王颖1,2，冯承莲2，黄文贤3，刘跃丹4，马燕2,5，张瑞卿6，吴丰昌2,*

1. 北京师范大学水科学研究院，北京 100875 2. 中国环境科学研究院 环境基准与风险评估国家重点实验室，北京100012 3. 北京师范大学数学科学学院，北京 100875 4. 环境保护部华南环境科学研究所 广东省水与大气污染防治重点实验室，广州510065 5. 青岛理工大学环境与市政工程学院 生物环保与绿色化工研究中心，青岛266033 6. 内蒙古大学环境与资源学院，呼和浩特010021

针对目前物种敏感度分布参数方法建模所存在的缺点，首次提出基于非参数核密度估计方法的物种敏感度分布模型，并提出相应的最优窗宽和检验方法。选用无机汞作为案例研究对象，利用非参数核密度估计方法和3种传统参数模型分别推导了保护我国水生生物的无机汞的急性水质基准值。结果表明，非参数核密度估计方法在推导无机汞水质基准中的稳健性和精确度都大大优于传统参数模型，能够更好地构建物种敏感度分布曲线。该方法的提出丰富了水质基准的理论方法学，为更好地保护水生生物提供了有力的支撑。

无机汞；淡水水生生物；水质基准；非参数核密度估计；物种敏感度分布

物种敏感度分布法(species sensitivity distribution, SSD)是由Kooijman[1]提出的一种用来推导水质基准[2-3]和生态风险评价[4]的科学研究方法。该方法认为不同的物种对相同污染物应存在遵循某种概率分布的敏感度差异，并假设选择的物种能够代表给定生态系统的群落结构，具有随机性，从而利用已知的毒性数据来拟合物种敏感度曲线，进而外推获得保护95%物种的基准值(hazardous concentration for 5% of species, HC5)或生态风险中受影响物种的比例(potentially affected fraction, PAF)[5]。很多学者围绕物种敏感度分布的概率建模开展了大量研究，传统研究思路是假设物种毒性数据服从某种参数分布，再利用统计分布对毒性数据进行概率拟合。目前通常用于物种敏感度分布推导HC5值的几种参数模型包括log-normal[6]、log-logistic[7]、Burr Type III[8]、Weibull[9]、Gompertz[10]、Sigmoid[11]、Gaussian[12]、Exponential Growth[13]。

然而参数模型对数据有较强的基本假定，常常与实际存在较大的差距，大量的研究也表明，实际采集到的毒性数据通常偏离既定的假设统计分布，得到的SSD参数估计不能总是取得满意的结果，而且也没有对所有毒性数据普遍适用的参数分布[14]，因此，依靠主观假设的参数分布拟合方法不具有通用性，最终容易造成基准推导值的失真。Posthuma[5]和Newman[10]分别提出了非参数的Monte Carlo和Bootstrap的方法构建SSD模型，相对于参数方法能够较客观地反映真实毒性数据信息。但是，Monte Carlo模拟依然是建立在特定分布的基础上[15]，而对有异常值的样本数据，Bootstrap法会使得数据结果更失真[16]，这都会造成模型的不确定性，而且Bootstrap法是基于一元统计得到危害浓度及其置信区间的分布[10]，并不是全体物种的分布，因此为SSD模型建立统一的估计方法迫在眉睫。

非参数核密度估计是一种不需要先验信息，不依赖于总体分布及其参数，完全以样本数据为基础，对数据限制较为宽松，一般不事先假定变量之间的结构关系，而是通过直接估计获得结构关系，能够很好地无偏估计数据的分布特征的方法[17]，天然具有稳健性。崔恒建等[18]结合实例探讨了非参数核密度估计在拟合直径分布中的应用。徐健君[19]成功地将非参数核密度估计方法应用在岷江冷杉天然林直径分布研究中。吴承祯等[20]应用非参数核密度估计很好地描述了群落物种多度分布。

本文拟采用非参数核密度估计的模型构建物种敏感度分布曲线，并提出相应的最优窗宽和检验方法。以无机汞为例，构建了无机汞的非参数核密度估计物种敏感度分布曲线，进一步验证了该方法用于推导水质基准的准确性和有效性。

1 研究方法(Methodology)

1.1 物种敏感度分布原理

物种敏感度分布是指在结构复杂的生态系统中，不同的物种对某一胁迫因素的敏感程度服从一定的概率分布，可以通过概率或者经验分布函数来描述不同物种样本对胁迫因素的敏感度差异[15]。通常计算基于给定样本的随机变量的分布密度函数，可以利用参数估计和非参数估计2类方法。参数估计中，往往假设数据分布符合某种特定的性态，然后在目标分布的函数族中确定特定的参数值，从而得到随机变量的分布密度函数。目前SSD采取的估计方法主要是将已知物种的毒性数据值按照从大到小的顺序排列，根据计算公式(1)[21]或(2)[13]计算每个物种的累积概率。

(1)

(2)

式中，p 为累积概率，i 为物种排序的等级，最小的为1，最大等级为n ，即为物种总数。然后根据参数或非参数的方法求解累积概率分布函数。Kolmogorov-Smirnov(K-S)检验用于检验参数模型的实用性。每个模型通过曲线拟合后，计算出的均方根误差(root mean square errors, RMSE)和判定系数(coefficients of determination, R2)用于描述参数模型的拟合程度；RMSE和误差平方和(sum of squares for error, SSE)用于描述非参数模型的拟合程度。拥有最小RMSE值和最大R2值的参数模型被认为是用于推导物种敏感度分布和水质基准值的最佳参数模型，拥有最小RMSE值和最小SSE值的非参数模型被认为是用于推导物种敏感度分布和水质基准值的最佳非参数模型[22]。

1.2 物种敏感度分布的非参数核密度估计

非参数核密度估计是指在给定样本后，仅从现有的样本数据出发，利用核密度函数估计的方法对其未知的总体密度函数的估计[23]。假设x1,x2,…xn是总体物种毒性数据X 独立同分布n 个的样本，X 的概率密度函数f(x) 未知，物种敏感度分布的非参数核密度估计为

(3)

其中，非参数核密度估计SSD使用的毒性数据样本(通常选用半数效应浓度或半数致死浓度EC50/LC50或无观察效应浓度NOEC)主要来自现有的数据库及其各类文献，经过物种、暴露时间、效应浓度的单位等数据筛选后获得，过程符合物种敏感度分布法毒性数据的筛选原则[15]。同时，根据统计学要求，非参数核密度估计通常建立在大样本统计的基础上[23]，毒性数据样本数量应至少超过30个。

1.3 核函数和最优窗宽的求取

一般先选定核函数，再确定最优窗宽。核函数K (x )通常选取关于原点对称并使得

(4)

常用的核函数有Parzen窗(Uniform)、三角(Triangle)、高斯(Gauss)、指数(Exponent)等。在独立同分布的情况下，核密度估计量具有逐点渐近无偏性、一致渐进无偏性和均方相合性等性质[24]。不同的核函数代表距离分配各样本点对密度贡献的不同情况，通常用渐近积分均方误差(AMISE)来度量[25]。根据Prakasa的研究[26]可知，满足核函数条件下的高斯核函数、均匀核函数和Epanechnikov核函数等的最优性几乎一致。因此，本文选用式(5)的标准高斯核函数。

(5)

核估计的关键是选取合理窗宽hn，这将直接关系核估计的精度，通常需要经过大量试验确定，当窗宽确定时，不同的核函数对估计的作用是等价的[27]。若采用高斯核函数，则根据经验法可得最优窗宽为[28]

(6)

1.4 模型检验

非参数核密度估计的物种敏感度分布模型采用K-S检验与后验检验的联合检验法，其中后验检验指定量评估概率模型与数据观测分布之间的差异，采用RMSE和SSE作为后验检验指标。通过K-S检验认为建立的模型分布成立，K-S检验统计量越小说明拟合优度越高[29]；RMSE和SSE越小，则说明非参数核密度估计模型的拟合程度越高。

2 案例研究(Case study)

2.1 无机汞毒性数据获取

汞(Hg)是重要的重金属，也是受关注的有毒污染物，它在天然水体里主要以无机形态存在，主要搜集Hg2+对中国淡水水生生物的毒性数据。毒性数据来自美国环保局ECOTOX数据库(http://cfpub.epa.gov/ecotox/)和中国知网(http://www/cnki/net/)收录的文献，主要来自于参考文献[21]。实验数据获得的准确性和可靠性均符合标准方法，具体筛选标准与文献[30]相同。相同物种具有多个毒性数据的情况下，取其所有效应浓度数据的几何平均值，称为种平均急性值(species mean acute value, SMAVs)。收集到的无机汞的慢性毒性数据较少，不足以构建物种敏感度曲线，所以仅使用无机汞的急性毒性数据作为案例研究。使用Matlab 2007b软件进行数据处理及模型构建。

2.2 无机汞的非参数核密度估计的急性物种敏感度分布构建

筛选出的Hg2+化合物急性毒性数据共90个物种，其中植物9种，脊椎动物33种，包括鱼类26种，两栖类7种；无脊椎动物48种，包括甲壳类25种，其他无脊椎动物23种，具体数据详见表1。

表1 无机汞对中国淡水水生生物急性毒性数据

注：使用的数据全部来自于参考文献[21]。

Note: All data used came from reference[21].

由表1可知，毒性数据范围为0.32～35 041.94，标准差达到4 199.01，差异太大，需要对原始数据做对数化处理以减小数据之间的差异性，达到数据平滑的效果，使得计算结果拟合度更高；同时也为了更好地同其他参数模型进行对比，因此在开展分析之前先对数据做对数化处理。经过处理后，采用高斯核函数对中国淡水水生生物的无机汞的急性毒性数据构建非参数核密度估计的物种敏感度分布，根据窗宽的经验公式计算窗宽h =0.3678，并对比4种其他的窗宽对拟合结果的影响(图1)。发现h 确实为最优窗宽，它从实际上兼顾了密度曲线的光滑性和模型的拟合优度，由此，确定了无机汞的非参数核密度估计的物种敏感度分布模型如式(7)所示。

(7)

2.3 不同模型的对比

对收集到的中国淡水水生生物的Hg2+的毒性数据做对数化处理并通过正态检验后，建立了物种敏感度分布的参数模型，并与非参数核估计模型进行了对比。采用极大似然估计方法得到3种拟合较好的normal分布、logistic分布和sigmoid分布的参数模型的概率密度函数，分布公式、估计值及模型检验结果见表2，3种参数模型与非参数核估计模型的累积概率分布的对比见图2。

从表1和图2中可以得出，对于所研究的Hg2+的中国淡水水生生物的毒性数据，所有模型均通过K-S检验，但本文提出的核密度估计模型与样本数据的经验分布K-S检验统计量最小，P 值最大，达到0.8974，后验检验指标RMSE和SSE也达到最小，说明拟合程度最好。进一步印证较低毒性效应值的拟

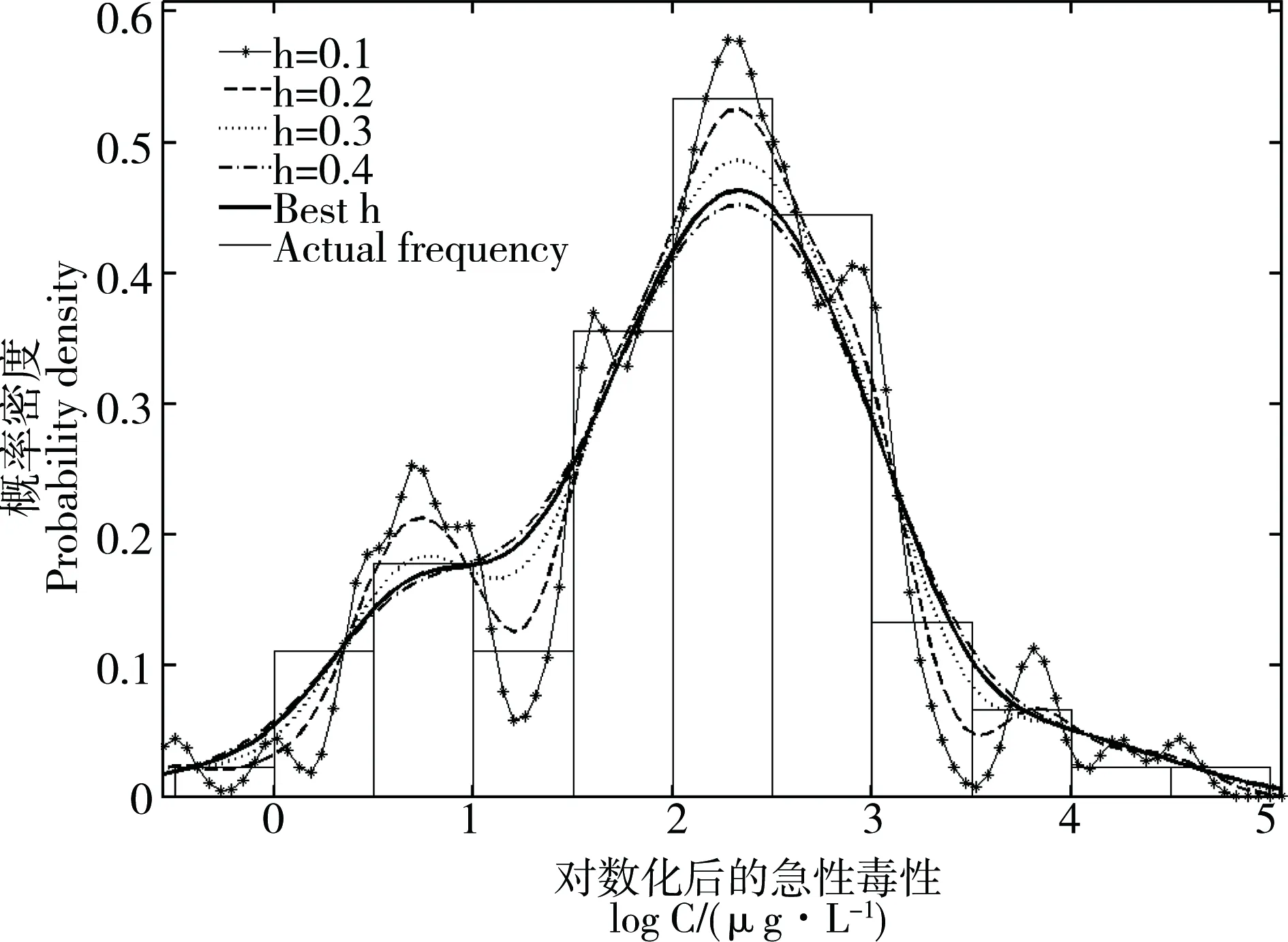
图1 无机汞对中国淡水水生生物的急性毒性数据构建非参数核密度估计的物种敏感度分布的不同窗宽的对比Fig. 1 Comparison among different bandwidth of species sensitivity distribution (SSDs) that is established by the non-parametric kernel density estimation for inorganic mercury to Chinese freshwater organisms

合程度，排序在前10%的物种的normal分布、logistic分布、sigmoid分布和非参数核密度估计模型的K-S检验统计量分别是0.0281、0.0363、0.0310和0.0244，其中非参数核密度估计模型最小，拟合程度最好。因此，本文提出的核密度估计模型对所选取的生物毒性数据不作预先分布的假设，对样本数据表现出很好的适应性，可以很好地弥补参数模型的缺陷，能够以较高的精度通过统计检验，获得最好的模拟效果。

另外，非参数核密度估计模型与Bootstrap法和Bootstrap回归法不同，前者可以像参数法一样获得全体物种的累积概率密度分布情况，后两者则是利用反复重抽样得到的随机替换样本构造经验分布函数或特定参数模型，只能计算特定统计量的估计值及置信区间[31]。同时，实验测得的毒性数据常常会出现异常值的情况，呈现偏态，服从相对“尖峰厚尾”的近似正态分布，参数模型往往不能很好地对这样的样本数据进行拟合；相反地，基于非参数核密度估计的SSD不需要先验信息，直接根据样本数据拟合，较参数模型对样本数据限制更为宽松，可以减少这些异常值点对SSD估计的影响，具有较好的稳健性。

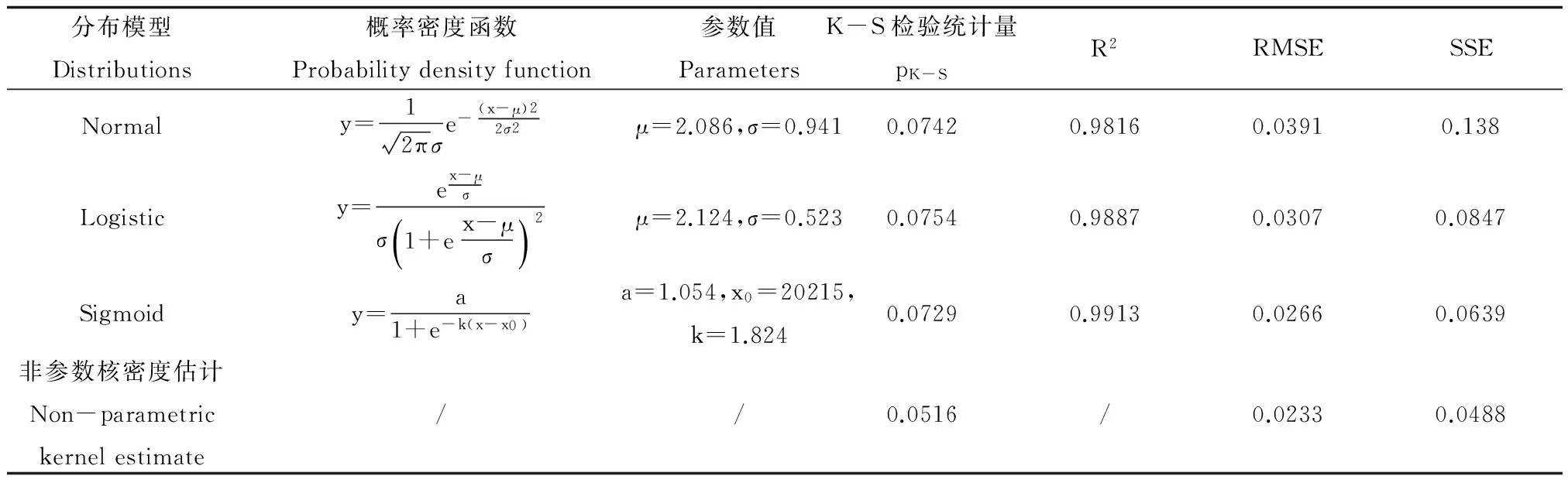
表2 各模型对对数化后的无机汞急性毒性数据的拟合结果

图2 三种参数模型与非参数核密度估计模型的累积概率密度函数对比Fig. 2 Comparison between three parametric distributions and non-parametric kernel estimate model of cumulative probability density function

2.4 不同模型得到的全部物种的HC5值对比

通常以保护95%物种的污染物浓度作为安全阈值，即HC5。因此，由normal分布、logistic分布、sigmoid分布参数模型和非参数核密度估计模型分别计算得到的HC5值为3.46、3.83、3.72和2.14μg·L-1。查找原始样本数据，可以发现，利用公式(2)计算得到的经验分布5%的累积概率所对应的样本物种是甲壳类棘爪网纹溞，其对应急性毒性值为2.9 μg·L-1，因此，4种估计模型的偏差分别为19.38%、31.94%、28.30%和26.23%。其中，normal分布参数模型和非参数核密度估计模型的偏差较小。为了更好地比较这2个模型的拟合效果，图3给出了这2种估计模型概率密度函数的对比。由图中可知，非参数核密度估计模型能够更好地反映物种毒性数据的总体变化趋势，更能反映样本的内在结构特征。进一步根据优先选择对于敏感物种毒性数据拟合较好的模型的原则[32]，非参数核密度估计模型较参数模型而言，得到的HC5值更加可靠。

2.5 无机汞的急性水质基准对比

根据式(8)计算得到急性水质基准值，目前大部分研究使用的评价因子取值为2[33]，本研究也采取相同的评价因子。

急性水质基准=急性HC5/AF

(8)

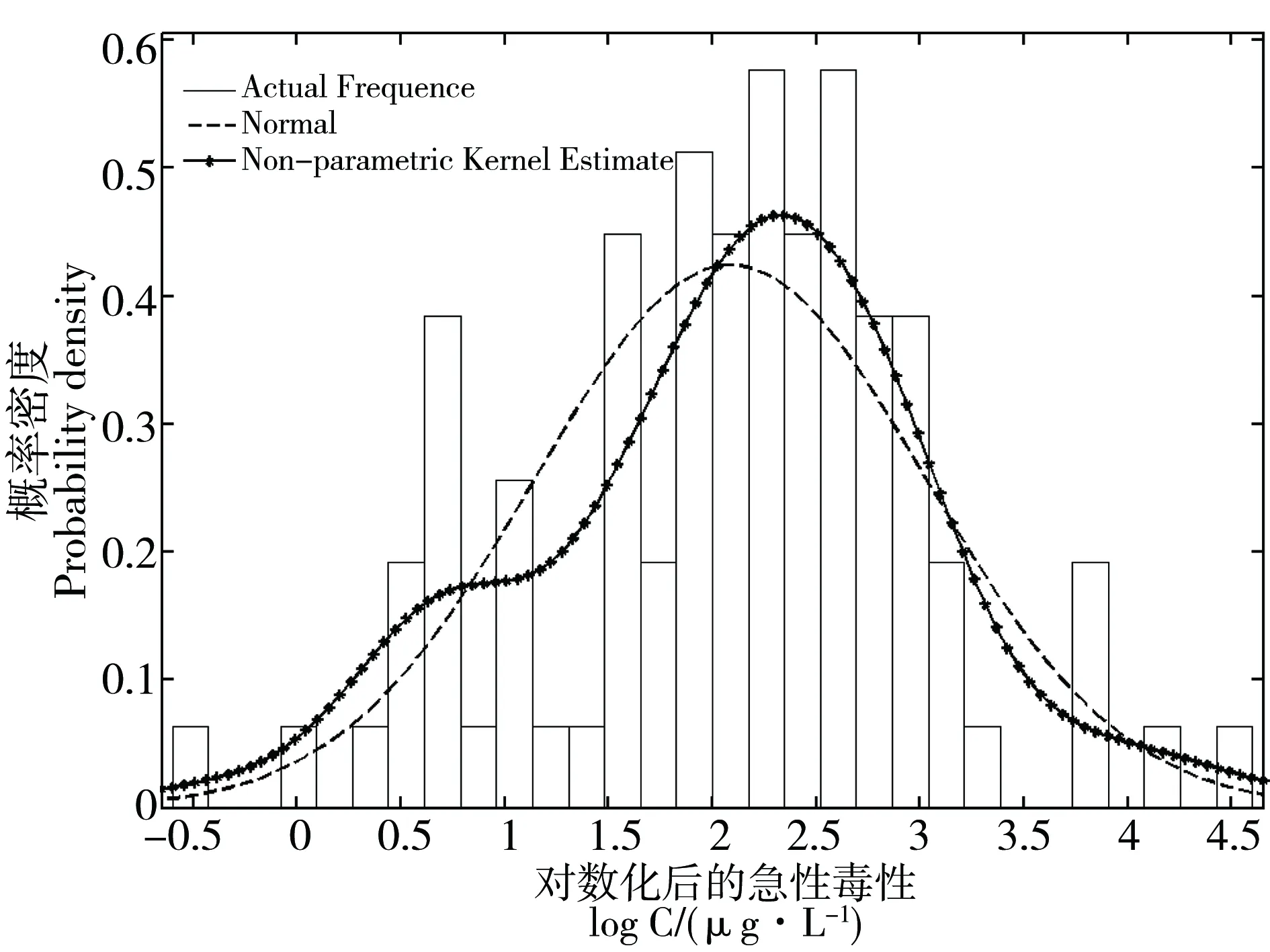
图3 normal分布参数模型与非参数核密度估计模型概率密度函数的对比Fig. 3 Comparison between normal distribution and non-parametric kernel estimate model of probability density function

将本研究得到的基准值同国内不同学者的研究结果及其他国家的急性水质基准值进行比较。张瑞卿等[21]使用Log-Slogistic3对物种急性毒性数据进行拟合；孔祥臻等[34]用BurrⅢ分布对Hg的SSD进行拟合；美国使用的是毒性百分数排序法，假设物种毒性数据符合对数-三角分布；澳大利亚采用BurrⅢ模型进行统计外推。表3给出了各研究推导出的急性水质基准对比结果。

表3 无机汞急性水质基准值对比

作为物种敏感度分布的重要组成部分，物种的组成和对污染物的敏感度能够直接影响物种敏感度分布推导结果的准确性，而不同生态系统中物种组成和物种敏感度与生物区密切相关[37]。例如，中国的鱼类代表种大多属于鲤科，而北美大多数鱼类属于鲑科。而本文主要选取的是代表中国广大水体环境中的淡水物种区系，因此同美国和澳大利亚的基准或标准值有所区别。但是，本研究与同是研究中国淡水水生生物的孔祥臻等[34]、张瑞卿等[21]和李会仙等[35]的研究结果差异较大，说明非参数核密度估计模型与参数模型间的差异性确实存在。其中，孔祥臻等[34]使用的样本物种仅为30种，数据集较小，因此存在较大的偏差，较难获取准确的参数估计值；张瑞卿等[21]使用的模型是log-sigmoid模型的一种变形，且其残差平方和为0.0664，大于本研究的0.0488，李会仙等[35]使用的是荷兰国立公共卫生与环境研究院开发的ETX2.0软件[6]，该软件使用的是log-Normal模型，仅用Anderson-Darling统计量检验了对分布的拟合情况，结果也较为粗糙(0.822<1.035)，由此说明非参数核密度估计模型比这2个参数模型的拟合更贴合样本数据，具有更高的准确性。同时，通过对比其他国家的基准值可以发现，非参数核密度估计模型推导出的急性基准值更加贴近实际，但是目前其他国家还没有利用非参数核密度估计模型对物种敏感度分布的研究结果。

2.6 模型的不确定性分析

实际物种毒性数据的有效性是模型确定的关键，因此样本数据的收集十分重要。本研究中案例使用的数据未考虑无机汞在生物体内的富集效应，也未考虑不同实验室数据的差异性。同时，污染物的毒性受到多种环境因素影响，例如水体硬度等，但目前没有足够数据来定量研究环境因素的影响，本文的模型也没有考虑环境因素。模型中核函数的窗宽估计依赖于具体的各物种毒性数据，因此在实际中窗宽的确定是较困难的问题，若h 太小会使拟合的物种敏感度分布曲线波动较大，不能反映内在规律；若h 太大则估计的物种敏感度分布曲线过于光滑，掩盖了其内在结构特征。本研究选取高斯核函数及其经验最优带宽建立了SSD分布，虽然得到了较好的结果，但仍可以根据拟合度和光滑度的实际情况对窗宽做适当调整，以获得更合适的分布密度。另外，非参数核密度估计通常建立在大样本统计的基础上，对小样本的密度估计并不太理想，因此对物种毒性数据样本较小(通常<30)的情况，需要对已构建的物种敏感度分布的非参数核密度估计模型做一定补充与改进。

本文提出的基于非参数核密度估计的物种敏感度分布模型既简单又灵活，具有很高的准确性和有效性，并给出了最优带宽选取和模型联合检验方法。选取的无机汞的水生生物毒性数据的案例研究，验证了非参数核密度估计方法在推导水质基准中的稳健性和适用性。该估计方法的提出丰富了水质基准的理论方法学，为更好地保护水生生物提供了更有力的支撑，可以考虑广泛应用于物种敏感度分布推导水质基准中的研究。

[1] Kooijman S A L M. A safety factor for LC50values allowing for differences in sensitivity among species [J]. Water Research, 1987, 21(3): 269-276

[2] Canadian Council of Resource and Environment Ministers (CCME). A protocol for the Derivation of Water Quality Guidelines for the Protection of Auqtic Life [R]. Ottawa: CCME , 2007

[3] Australian and New Zealand Environment and Conservation Council and Agriculture and Resource Management Council of Australian and New Zealand (ANZECC, ARMCANZ). Peper No.4 Australian and New Zealand Guidelines for Fresh and Marine Water Quality [R]. Canberra: ANZECC, ARMCANZ, 2000

[4] US Environmental Protection Agency (US EPA). Guidelines for Ecological Risk Assessment [R]. Washington DC: US EPA, 1998

[5] Posthuma L, Suter II G, Traas T P. Species Sensitivity Distributions in Ecotoxicology [M]. Boca Raton FL: Lewis Publishers, 2002: 1-198

[6] Van Vlaardingen P L A, Traas P T, Wintersen A M, et al. Etx2. 0. A program to calculate hazardous concentrations and fraction affected, based on normally-distributed toxicity data. RIVM report (and software) 601501028/2004 [R]. Bilthoven: National Institute for Public Health and the Environment (RIVM), 2004

[7] Pennington D W. Extrapolating ecotoxicological measures from small data sets [J]. Ecotoxicology and Environmental Safety, 2003, 56(2): 238-250

[8] Shao Q. Estimation for hazardous concentrations based on NOEC toxicity data: An alternative approach [J]. Environmetrics, 2000, 11(5): 583-595

[9] Van Straalen N M. Threshold models for species sensitivity distributions applied to aquatic risk assessment for zinc [J]. Environmental Toxicology and Pharmacology, 2002, 11(3-4): 167-172

[10] Newman M C, Ownby D R, Mezin L C, et al. Applying species-sensitivity distributions in ecological risk assessment: Assumptions of distribution type and sufficient numbers of species [J]. Environmental Toxicology and Chemistry, 2000, 19(2): 508-515

[11] 曹宇静, 吴丰昌. 淡水中重金属镉的水质基准制定[J]. 安徽农业科学, 2010, 38(3): 1378-1380, 1437

Cao Y J, Wu F C. Establishment of water quality criteria for cadmium in freshwater [J]. Journal of Anhui agriculture, 2010, 38(3): 1378-1380, 1437 (in Chinese)

[12] 吴丰昌, 冯承莲, 曹宇静, 等. 锌对淡水生物的毒性特征与水质基准的研究[J]. 生态毒理学报, 2011, 6(4): 367-382

Wu F C, Feng C L, Cao Y J, et al. Toxicity characteristic of zinc to freshwater biota and its water quality criteria [J]. Asian Journal of Ecotoxicology, 2011, 6(4): 367-382 (in Chinese)

[13] 吴丰昌, 冯承莲, 张瑞卿, 等. 我国典型污染物水质基准研究[J]. 中国科学: 地球科学, 2012, 42(5): 665-672

Wu F C, Feng C L, Zhang R Q, et al. Derivation of water quality criteria for representative water-body pollutants in China [J]. Science in China: Earth Science, 2012, 42(5): 665-672 (in Chinese)

[14] 吴丰昌, 孟伟, 曹宇静, 等. 镉的淡水水生生物水质基准研究[J]. 环境科学研究, 2011, 24(2): 172-184

Wu F C, Meng W, Cao Y J, et al. Derivation of aquatic life water quality criteria for cadmium in freshwater in China [J]. Research of Environmental Science, 2011, 24(2): 172-184 (in Chinese)

[15] 陈波宇, 郑斯瑞, 牛希成, 等. 物种敏感度分布及其在生态毒理学中的应用[J]. 生态毒理学报, 2010, 5(4): 491-497

Chen B Y, Zheng S R, Niu X C, et al. Species sensitivity distribution and its application in ecotoxicology [J]. Asian Journal of Ecotoxicology, 2010, 5(4): 491-497 (in Chinese)

[16] 潘海涛. Bootstrap方法在非参数核估计中的研究与应用[J]. 统计与决策, 2010(23): 22-24

[17] Rosenblatt M. Remarks on some nonparametric estimates of a density function [J]. The Annals of Mathematical Statistics, 1956, 27(3): 832-837

[18] 崔恒建, 王雪峰. 核密度估计及其在直径分布研究中的应用[J]. 北京林业大学学报, 1996, 18(2): 67-72

Cui H J, Wang X F. Property of kernel density estimation and application in the diameter distribution [J]. Journal of Beijing Forestry University, 1996, 18(2): 67-72 (in Chinese)

[19] 徐健君. 非参数核密度估计在岷江冷杉天然林直径分布研究中的应用[J]. 甘肃林业科技, 1999, 24(4): 22-24, 28

Xu J J. An application of non-parameter nucle-densiety estimation on research of diameter distribution of Abies f axoniana natural forest [J]. Journal of Gansu Forestry Science and Technology, 1999, 24(4): 22-24, 28 (in Chinese)

[20] 吴承祯, 洪伟, 吴继林, 等. 两种珍稀植物群落物种多度分布的核方法研究[J]. 热带亚热带植物学报, 2000, 8(4): 301-307

Wu C Z, Hong W, Wu J L, et al. Studies on kernel density estimation of species abundance distribution in two communities of rare and endangered plants [J]. Journal of Tropical and Subtropical Botany, 2000, 8(4): 301-307 (in Chinese)

[21] 张瑞卿, 吴丰昌, 李会仙, 等. 应用物种敏感度分布法研究中国无机汞的水生生物水质基准[J]. 环境科学学报, 2012, 32(2): 440-449

Zhang R Q, Wu F C, Li H X, et al. Deriving aquatic water quality criteria for inorganic mercury in China by species sensitivity distributions [J]. Acta Scientiae Circumstantiae, 2012, 32(2): 440-449 (in Chinese)

[22] Liu Y D, Wu F C, Mu Y S, et al. Setting water quality criteria in China: Approaches for developing species sensitivity distributions for metals and metalloids [J]. Reviews of Environmental Contamination and Toxicology, 2014(230): 35-57

[23] 吴喜之. 非参数统计[M]. 北京: 中国统计出版社, 1999: 175-187

[24] 陈希孺, 柴根象. 非参数统计教程[M]. 上海: 华东师范大学出版社, 1993: 247-270

[25] 赵渊, 沈智健, 周念成, 等. 基于序贯仿真和非参数核密度估计的大电网可靠性评估[J]. 电力系统自动化, 2008, 32(6): 14-19

Zhao Y, Shen Z J, Zhou N C, et al. Reliability assessment of bulk power systems utilizing sequential simulation and nonparametric kernel density estimation [J]. Autonation of Electric Power Systems, 2008, 32(6): 14-19 (in Chinese)

[26] Prakasa Rao B L S. Nonparametric Functional Estimation [M]. New York: Academic Press, 1983: 22-198

[27] Epanechnikov V A. Non-parametric estimation of a multivariate probability density [J]. Theory of Probability & Its Applications, 1969, 14(1): 153-158

[28] 李竹渝, 鲁万波, 龚金国. 经济, 金融计量学中的非参数估计技术[M]. 北京: 科学出版社, 2007: 10-20

[29] 颜伟, 任洲洋, 赵霞, 等. 光伏电源输出功率的非参数核密度估计模型[J]. 电力系统自动化, 2013, 37(10): 35-40

Yan W, Ren Z Y, Zhao X, et al. Probabilistic photovoltaic power modeling based on nonparametric kernel density estimation [J]. Autonation of Electric Power Systems, 2013, 37(10): 35-40 (in Chinese)

[30] 吴丰昌, 冯承莲, 曹宇静, 等. 我国铜的淡水生物水质基准研究[J]. 生态毒理学报, 2011, 6(6): 617-628

Wu F C, Feng C L, Cao Y J, et al. Aquatic life ambient freshwater quality criteria for copper in China [J]. Asian Journal of Ecotoxicology, 2011, 6(6): 617-628(in Chinese)

[31] Grist E P, Leung K M, Wheeler J R, et al, Better bootstrap estimation of hazardous concentration thresholds for aquatic assemblages [J]. Environmental Toxicology and Chemistry, 2002, 21(7): 1515-1524

[32] 吴丰昌. 水质基准理论与方法学及其案例研究[M]. 北京: 科学出版社, 2012: 77-87

[33] Van Sprang P A, Verdonck F A M, Vanrolleghem P A, et al. Probabilistic environmental risk assessment of zinc in Dutch surface waters [J]. Environmental Toxicology and Chemistry, 2004, 23(12): 2993-3002

[34] 孔祥臻, 何伟, 秦宁, 等. 重金属对淡水生物生态风险的物种敏感性分布评估[J]. 中国环境科学, 2011, 31(9): 1555-1562

Kong X Z, He W, Qin N, et al. Assessing acute ecological risks of heavy metals to freshwater organism by species sensitivity distributions [J]. China Environmental Science, 2011, 31(9): 1555-1562 (in Chinese)

[35] 李会仙, 张瑞卿, 吴丰昌, 等. 中美淡水生物区系中汞物种敏感度分布比较[J]. 环境科学学报, 2012, 32(5): 1183-1191

Li H X, Zhang R Q, Wu F C, et al. Comparison of mercury species sensitivity distributions of freshwater biota in China and the United States [J]. Acta Scientiae Circumstantiae, 2012, 32(5): 1183-1191 (in Chinese)

[36] US EPA. National Recommended Water Quality Criteria [R]. Washington DC: Office of Research and Development, 2012

[37] Brock T, Arts G H P, Maltby L, et al. Aquatic risks of pesticides, ecological protection goals, and common aims in European Union legislation [J]. Integrated Environmental Assessment and Management, 2006, 2(4): e20-e46

◆

Non-Parametric Kernel Density Estimation of Developing Species Sensitivity Distributions

Wang Ying1,2, Feng Chenglian2, Huang Wenxian3, Liu Yuedan4, Ma Yan2,5, Zhang Ruiqing6, Wu Fengchang2,*

1. College of Water Sciences, Beijing Normal University, Beijing 100875, China 2. State Key Laboratory of Environmental Criteria and Risk Assessment, Chinese Research Academy of Environmental Science, Beijing 100012, China 3. School of Mathematical Sciences, Beijing Normal University, Beijing 100875, China 4. The Key Laboratory of Water and Air Pollution Control of Guangdong Province, South China Institute of Environmental Sciences, the Ministry of Environment Protection of PRC, Guangzhou 510065, China 5. Research Center of Environmental Biology and Green Chemistry, School of Environmental and Municipal Engineering, Qingdao Technological University, Qingdao 266033, China 6. College of Environment and Resources, Inner Mongolia University, Huhhot 010021, China

27 May 2014 accepted 4 July 2014

To address the inadequacies associated with parametric density estimations for species sensitivity distributions, we developed a new probabilistic model based on non-parametric kernel density estimation and proposed related optimal bandwidths and testing methods as well. With inorganic mercury as the target compound, the non-parametric kernel density estimation method and three conventional parametric density estimation methods were used to derive acute water quality criteria for protection of aquatic species in China. The results demonstrated that the new probabilistic model was superior over the conventional parametric density estimations in deriving water quality criteria for inorganic mercury, as well as in constructing species sensitivity distribution. The proposed method has enriched the methodological foundation for water quality criteria and provided solid support for protection of aquatic organisms.

inorganic mercury; freshwater organisms; water quality criteria; non-parametric kernel density estimation; species sensitivity distribution

环保公益项目(201309060；201409037) ；国家自然科学基金重点项目(41130743)

王颖(1989-)，女，博士，研究方向为环境基准与风险评估，E-mail: wy2012bnu@126.com；

*通讯作者(Corresponding author)，E-mail: wufengchang@vip.skleg.cn

10.7524/AJE.1673-5897.20140527002

2014-05-27 录用日期：2014-07-04

1673-5897(2015)1-215-10

X171.5

A

吴丰昌(1964—)，男，博士，研究员，博士生导师，主要研究方向为湖泊污染过程、天然有机质与水环境质量基准。

王颖, 冯承莲, 黄文贤, 等. 物种敏感度分布的非参数核密度估计模型[J]. 生态毒理学报, 2015, 10(1): 215-224

Wang Y, Feng C L, Huang W X, et al. Non-parametric kernel density estimation of developing species sensitivity distributions [J]. Asian Journal of Ecotoxicology, 2015, 10(1): 215-224(in Chinese)