基于快速匹配追踪算法的地震道集剩余时差校正

张汛汛,张繁昌,刘汉卿

(中国石油大学(华东)地球科学与技术学院,山东青岛266580)

基于快速匹配追踪算法的地震道集剩余时差校正

张汛汛,张繁昌,刘汉卿

(中国石油大学(华东)地球科学与技术学院,山东青岛266580)

为提取正确的AVO信息和获得高信噪比、高分辨率的叠加剖面,需要消除CMP道集上的剩余时差,校平同相轴。为此,给出了一种基于匹配追踪(Matching Pursuit,MP)算法的地震道集剩余时差校正方法。利用匹配追踪算法在地震信号分解与重构方面的优势,将CMP道集信号分解为不同的子波,对各个子波分别进行剩余时差校正,再用校正后的子波重构出消除剩余时差后的地震道。同时,为提高匹配追踪算法的计算效率,利用相位展开法得到稳定的瞬时频率,以瞬时频率为中心进行扫描,快速得到最优匹配频率。理论模型和实际资料的测试结果表明,这种方法不仅可以提高匹配追踪算法的计算效率,而且还能很好地校平CMP道集同相轴。

匹配追踪；相位展开；信号分解与重构；剩余时差校正

叠前AVO反演从提出后便得到了广泛的应用,如层状介质AVO叠前反演[1]、基于叠前地震道集的AVA多频信息同时反演[2]和基于t分布[3]的叠前AVO反演等。该方法在提取道集信息时,要求地震道集是校平的,这样才能提取正确的AVO信息，但道集在实际的动、静校正后往往会存在剩余时差,使CMP道集同相轴无法校平,影响反演效果。为消除剩余时差,人们提出了许多方法。傅旦丹[4]在互相关剩余时差校正方法的基础上,侧重研究模型道的形成；王开燕等[5]在2007年提出了相位替换剩余时差校正方法；吴波等[6]改进了最大能量剩余静校正方法,以提高信噪比、压制“周波跳跃”现象；马季军等[7]对相关法校正剩余时差的方法进行改进,提出通过提取地震道中不同时刻极值点时移量校正时差的方法；慎国强等[8]在2010年将地震信号引入时频域,在时频域拾取并校正剩余时差；2014年许自龙等[9]提出用常规多项式拟合及叠加技术消除剩余时差的方法。

匹配追踪(Matching Pursuit,MP)算法由Mallat等[10]于1993年提出,是一种高精度的地震信号分解与重构算法,但计算效率一直制约着该算法的应用。为提高算法计算效率,国内外学者对算法进行了多种改进。Liu等[11-12]分别于2004年和2005年先后建立了基于Ricker和Morlet子波的原子库,大大缩减了原子库的规模；张繁昌等[13]在2010年提出动态子波库的匹配追踪算法；Wang[14]提出多通道匹配追踪算法；为减小原子库的规模,张繁昌等[15]在2012年提出基于正交时频原子的原子库；2013年张繁昌等[16]将地震信号引入复数域,减少了子波的控制参数。

本文通过对不同匹配追踪算法和剩余时差校正方法在信号分解与重构上的优势分析,提出一种基于快速匹配追踪算法的剩余时差校正方法,利用匹配追踪算法在地震信号分解与重构方面的优势,将地震信号分解为不同的子波,然后对各个子波进行剩余时差校正,最后重构地震信号,得到消除剩余时差后的道集。为提高匹配追踪算法的计算效率,利用相位展开法[17]对相位进行处理,得到稳定瞬时频率,以瞬时频率为中心进行扫描匹配,这样能够快速得到匹配频率,从而提高计算效率。资料测试分析发现,该方法不仅可以提高匹配追踪算法的计算效率,而且还能很好地消除同相轴错位现象,提高道集同相轴的连续性。

1 方法原理

1.1 快速匹配追踪算法

匹配追踪算法是通过创建一个超完备的子波原子库,使地震信号根据自身特点自适应地在这个完备原子库中展开,通过选择最优子波,最后将地震信号表示为这些基本原子的线性组合。经过匹配追踪分解后,地震信号可以表示为多个时频原子的线性组合:

(1)

式中：bn,tn,fn和φn分别表示各个子波的振幅、时移、主频和相位。

传统的匹配追踪算法因每次确定最优子波都需要扫描整个完备子波库,大大增加了计算量,制约着计算效率的提高。复数域双参数匹配追踪算法可以在复数域通过阻尼最小二乘得到复振幅[16],从而同时确定实振幅和相位参数,但最优频率参数仍然需要扫描整个子波库来确定。为了进一步提高计算效率,我们对复数域双参数匹配追踪算法进行了改进。改进型双参数动态匹配追踪是在复数域双参数动态扫描的基础上,引入地震信号的瞬时特征以减小频率扫描范围的一种匹配追踪方法。在复数域中,地震信号的瞬时频率可以表示为：

(2)

在求取瞬时频率的过程中,我们需要得到地震信号包络极大值附近每一个采样点的瞬时相位值,即：

(3)

式中：h*(t)表示地震信号h(t)的希尔伯特变换。由公式(3)可以看出每一个时间点的相位是随信号变化的,这就可能使极大值前、后采样点的相位差值为负值,从而使我们得到的瞬时频率为负值,但在匹配追踪算法中负值频率是不能存在的,因此此处的瞬时频率不具有实际意义。

产生上述问题的原因在于,在求取主值相位的方法中,由于应用反三角函数,求得的只是位于[-2π,0]的包裹相位[17]。要想获得待测物理量的信息,就必须首先从包裹相位中恢复出原始的连续相位,这一过程叫做相位展开[17]。为了重建被测信号的真实相位图,必须对包裹相位进行相位连续化处理来消除2π跳变。最传统的相位连续化方法是逐行或逐列比较相邻两点的相位值,如果它们的相位差超过了π,那么就通过加/减2π的整数倍值来使相位差小于π。这样处理后相位值逐点递增,使前、后采样点的相位差为正值,从而得到具有实际意义的瞬时频率。以极大值处瞬时频率为中心,在一定范围内扫描频率以得到最优匹配频率,这样就可以大大缩小频率的扫描范围,从而提高匹配追踪算法的运算效率。

1.2 地震道集剩余时差校正

在动、静校正后的CMP道集上往往还存在剩余时差,这对地震资料的分辨率和信噪比有很大影响,因此,必须进行剩余时差校正。本文基于改进后的匹配追踪算法,利用该算法在地震信号分解与重构方面的优势,把信号分解为一系列不同的子波,然后针对偏移距和子波频率等控制因子对子波进行剩余时差校正,最后将校正后的各个子波重构,得到剩余时差校正后的地震道。

首先建立模型道。零偏移距道往往是不存在的,每个道集中的最小偏移距道可以近似看作零偏移距道,但是单独一个道的信噪比是不高的,而叠加道可以有效压制随机干扰信号的影响,增强有效信号。所以,一般采用一定偏移距范围内道集的叠加道作为模型道。然后,在匹配追踪算法中,将模型道和任一地震道进行匹配分解,得到每次迭代产生的最优子波,对分解产生的各个最优子波分别进行剩余时差校正。设任一地震道上匹配出的一个子波的中心时间是t1,在模型道上相应的t1时刻附近一定时窗T范围内寻找最近的一个子波,设中心时间为t2,那么就可以得到地震道上子波的时差值Δt=t1-t2,然后校正子波的中心时间为t=t1±t2,按照上述的时差校正原理对所有的最优子波进行时差校正。将校正后的最优子波用于地震信号的重构,得到经过时差校正后的地震道。

时窗范围的选择受偏移距和频率参数的影响,针对不同偏移距的道集和匹配出的高、低频子波,可以用(4)式求取时窗范围T：

(4)

式中：t0表示设定的初始时窗；Δ是一个固定增量,可以根据地震资料灵活设定；α表示受偏移距和子波频率影响的控制因子。针对不同的偏移距以及不同的子波频率段,计算得到不同的控制因子,最后用不同的时窗范围值进行子波时差校正。

图1为剩余时差校正原理图。图中第1道表示模型道某次迭代出的最优子波,第2道为任一地震道相同迭代次数得到的最优子波,tm表示待校正道上某个子波的中心时间,第3道是经过时差校正后的地震道。

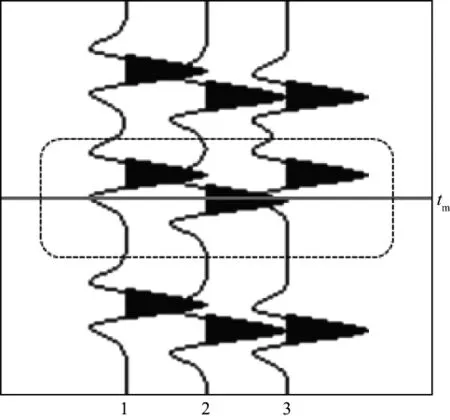
图1 剩余时差校正原理

2 匹配追踪精度与计算速度测试

为了测试改进后匹配追踪算法的精度和鲁棒性,用表1的子波参数合成一个地震记录,如图2中红色曲线所示。

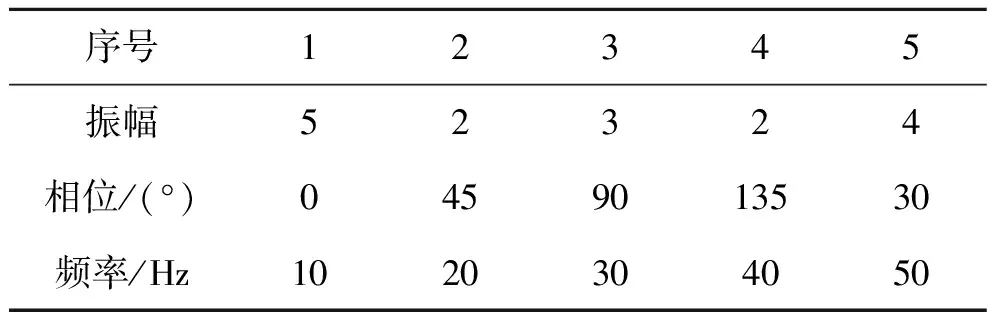
表1 合成地震记录参数

然后,用改进的匹配追踪算法对合成地震记录进行匹配分解。经过两次迭代后,合成记录被完全分解出来。图2给出了信号的分解过程。可以看出,经过一次迭代，振幅比较大的3个子波被匹配出来,剩下的两个振幅较小的子波在第2次迭代时被匹配出来。经过匹配追踪后的重构地震记录如图3所示。可以看出,重构信号近似于原始合成信号,并且最后的残差值几乎为0,表明改进后的算法具有很高的精确度。

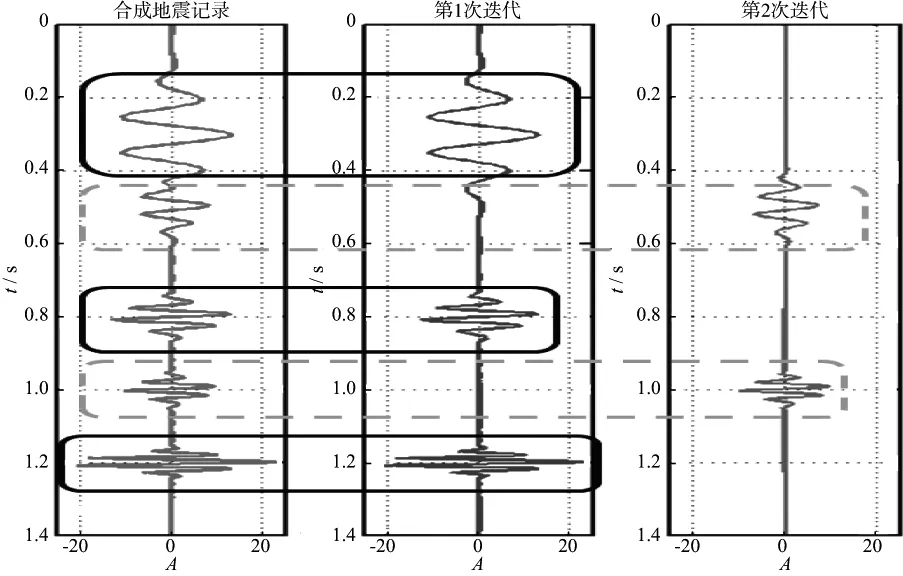
图2 合成地震记录分解过程

为了检验算法的鲁棒性,我们在合成地震记录中加入随机噪声,然后进行匹配分解。图4为加入随机噪声的合成地震记录以及经过匹配追踪后重构的地震记录。由图4可见,虽然加入了随机噪声,但改进后的匹配追踪算法还是能够很好地重构出信号,并且消除随机噪声,表明本文算法具有良好的稳定性。

在保证算法的匹配精度后,提高算法的计算效率成为另一个亟待解决的问题。为了检验算法的计算效率,我们分别用原有的复数域双参数算法和改进后的双参数算法对实际地震数据进行匹配分解,然后对比它们的重构结果和计算效率。

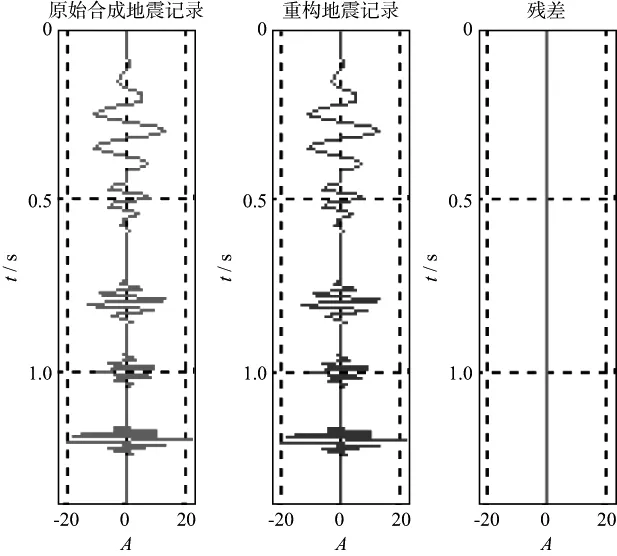
图3 不含噪声的合成地震记录经匹配追踪后的重构地震记录

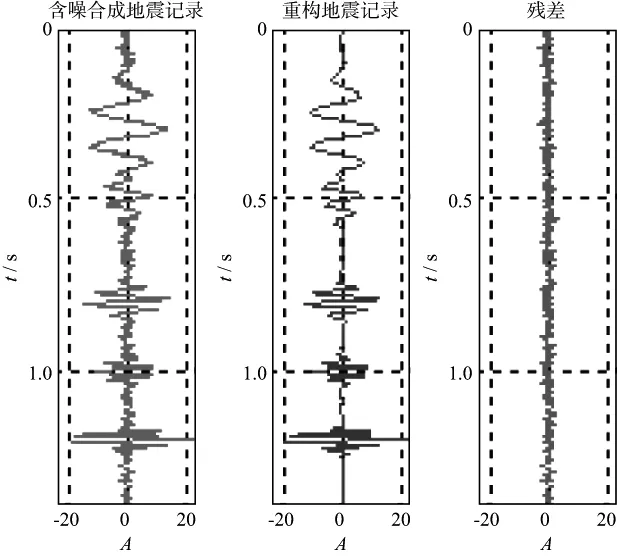
图4 含噪合成地震记录经匹配追踪后的重构地震记录

图5a和图5b分别给出了使用复数域双参数匹配追踪算法和改进型双参数匹配追踪算法对实际地震道进行匹配分解与重构的结果。从图5可以看出,两种算法都可以在保证匹配精度的基础上对信号进行分解与重构。但是两种算法在计算效率方面却有很大的差别。图5中两种算法的结果都是经过5次迭代后得到的,但分析发现,复数域双参数匹配追踪算法需要2.515s完成对数据道的匹配,而改进型双参数匹配追踪算法只耗时0.322s,计算速度是前者的7.8倍,大大提高了计算效率,能够满足三维工区叠前地震道集大数据量计算的要求。

图5 采用复数域双参数算法(a)和改进型双参数算法(b)对实际资料进行匹配分解并重构后的结果

3 应用效果分析

3.1 理论模型测试

为了验证本文方法的有效性,建立如图6a所示的一个模拟CMP道集记录。该道集共201个采样点,20道。为了模拟实际资料中存在剩余时差的情况,在每个层位的到达时间中均加入随机时移,如图6b所示。原始道集中加入随机时移后,道集同相轴的连续性明显变差,因而叠加信号的主频变低,频带变窄,降低了地震剖面的分辨率。为了消除剩余时差的影响,需要对其进行校正。图6c 给出了基于快速匹配追踪算法剩余时差校正后的道集。从图6c可以看出,时移得到消除,同相轴被校平,各个波形出现的位置准确,与不加时移的模型CMP道集非常接近。由以上对比分析可以看出,基于快速匹配追踪算法的地震道集校正方法可以有效地消除道集中的剩余时差,校平同相轴。

图7给出了含时移且加噪的CMP模型道集及其经剩余时差校正后的结果。其中,图7a是在加时移的模型CMP道集中加入随机噪声后得到的道集。利用基于快速匹配追踪算法的地震道集校平方法对图7a中道集进行时差校正,结果如图7b 所示。从图7a和图7b可以看出,道集中的时差得到消除,同相轴连续性明显变好,表明本文方法具有良好的鲁棒性。

图6 理论模型剩余时差校正效果分析

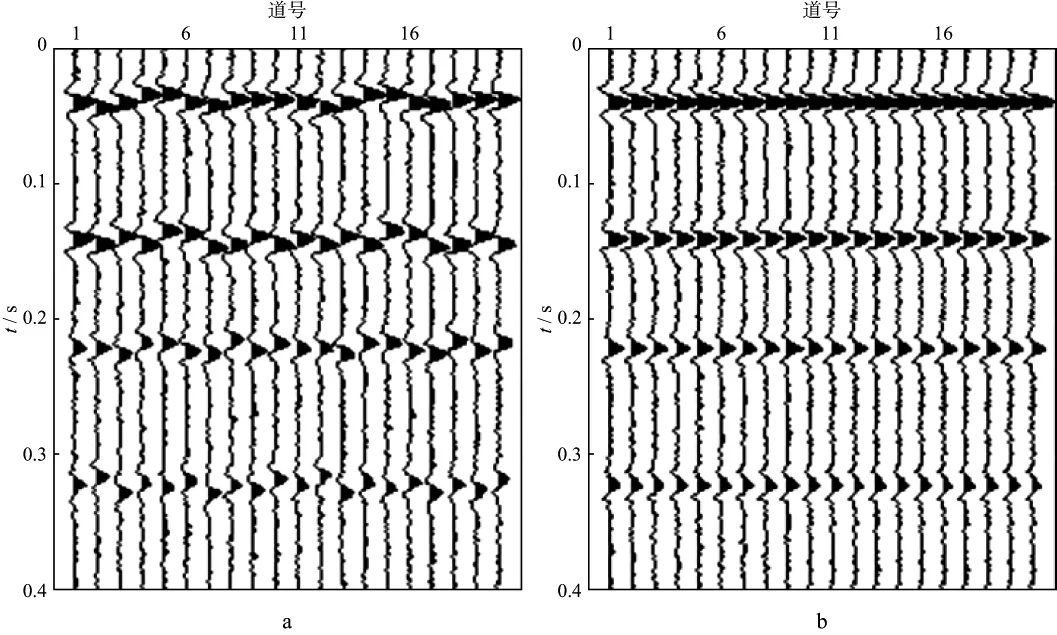
图7 含时移且加噪的CMP模型道集(a)及其经剩余时差校正后的结果(b)

为对比分析分子波时差校正和统一时差校正的效果,建立了如图8a所示的随机时移模型道集。图8b和图8c分别是采用分子波时差校正和统一时差校正后的道集。可以看出,对于具有强振幅的优势子波,两种方法均能很好地校正时差；但是对于距优势子波很近的弱振幅子波,分子波时差校正方法能有效校正时差,而统一时差校正方法的校正效果不佳。

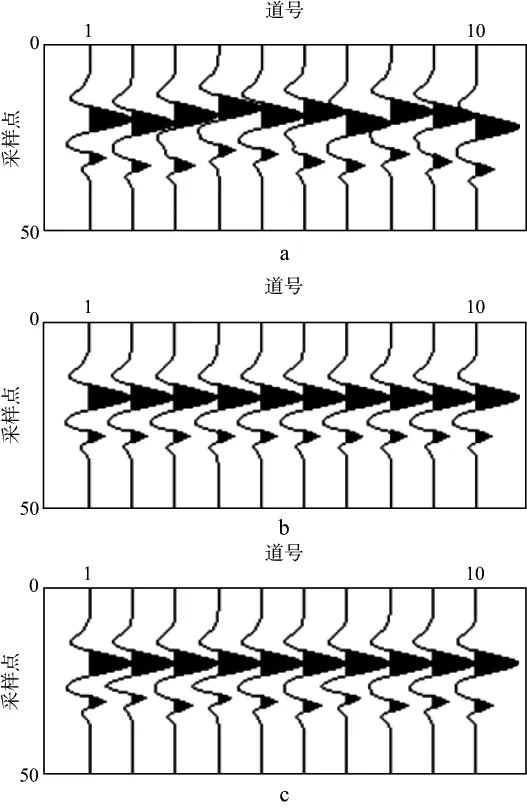
图8 统一时差校正和分子波时差校正效果对比

3.2 实际资料分析

图9a是从某工区实际地震资料中抽取的一个CMP道集,共27道,采样间隔2ms,每道601个采样点。该道集已经经过叠前去噪、反褶积以及动、静校正处理,但仍然存在一些剩余时差。图9b是以图9a的叠加道作为参考道,经过基于快速匹配追踪算法的地震道集剩余时差校正后的CMP道集。从图9b 中可以看出,道集的同相轴错位现象明显减小,各道的波形出现位置准确,同相轴基本校平,光滑性比处理前更好,连续性也明显变好,剩余时差得到了有效消除,有利于正确提取AVO信息。

图10是基于图9剩余时差校正前、后的CMP道集在第571个采样点处提取的振幅随偏移距变化的曲线(黑色曲线和红色曲线分别是基于快速匹配追踪算法剩余时差校正前、后CMP道集提取的关系曲线)。很明显,在选定某一点提取振幅时,由剩余时差校正前CMP道集提取的振幅随偏移距变化曲线奇异值点很多,因为该采样点处道集中存在剩余时差,同相轴不平；经过剩余时差校正后,同相轴被拉平,从而能提取正确的AVO信息,进而提高叠前反演的精度。

图9 某工区实际地震资料剩余时差校正前(a)、后(b)的道集

图10 剩余时差校正前、后振幅随偏移距的变化曲线(第571个采样点处)

4 结论

本文给出了一种基于匹配追踪算法的剩余时差校正方法,利用匹配追踪算法在地震信号分解与重构上的优势,将地震信号分解为不同的子波,然后对各个子波进行时差校正,最后用剩余时差校正后的子波重构出地震道；同时,为提高匹配追踪算法的计算效率,将瞬时相位解缠绕,计算得到稳定的瞬时频率,以得到的瞬时频率为中心扫描得到最优频率,减少计算量。理论模型测试和实际资料应用表明,经过校正后的CMP道集的同向性得到增强,同相轴错位现象得到明显消除,这有利于提高地震资料的分辨率和信噪比,正确提取AVO信息。

[1] 陈建江,印兴耀,张广智.层状介质AVO叠前反演[J].石油地球物理勘探,2006,41(6):656-662 Chen J J,Yin X Y,Zhang G Z.AVO pre-stack inversion of layered medium[J].Oil Geophysical Prospecting,2006,41(6):656-662

[2] 张繁昌,代荣获,刘汉卿,等.叠前地震道集AVA多频信息同时反演[J].石油物探,2014,53(4):453-460 Zhang F C,Dai R H,Liu H Q,et al.Multi-frequency AVA simultaneous inversion for prestack seismic gathers[J].Geophysical Prospecting for Petroleum,2014,53(4):453-460

[3] 印兴耀,周琪超,宗兆云,等.基于t分布为先验约束的叠前AVO反演[J].石油物探,2014,53(1):84-92 Yin X Y,Zhou Q C,Zong Z Y,et al.Pre-stack AVO inversion based on t distribution as the prior constraint[J].Geophysical Prospecting for Petroleum,2014,53(1):84-92

[4] 傅旦丹.静校正中剩余时差的拾取[J].江汉石油学院学报,1991,13(4):15-18 Fu D D.Pick up residual moveout of static correction[J].Journal of Jianghan Petroleum Institute,1991,13(4):15-18

[5] 王开燕,李慧,官波,等.相位剩余时差校正方法在提高分辨率中的应用[J].大庆石油学院学报,2007,31(6):14-17 Wang K Y,Li H,Guan B,et al.Residual phase moveout correction method applied in improving the resolution[J].Journal of Daqing Petroleum Institute,2007,31(6):14-17

[6] 吴波,尹成,潘树林,等.最大能量法剩余静校正的改进[J].石油地球物理勘探,2010,45(3):350-354 Wu B,Yin C,Pan S L,et al.The maximum energy method improved of the residual static correction[J].Oil Geophysical Prospecting,2010,45(3):350-354

[7] 马永军,王季.一种改进的时间域剩余动校正方法[J].石油物探,2010,49(3):245-247 Ma Y J,Wang J.An improved method for time-domain residual NMO[J].Geophysical Prospecting for Petroleum,2010,49(3):245-247

[8] 慎国强,王玉梅,孟宪军,等.基于时频分析的地震道集校平技术应用[J].中国石油大学学报(自然科学版),2010,34(1):34-36 Shen G Q,Wang Y M,Men X J,et al.The application of seismic gather leveling technology based on time-frequency analysis[J].Journal of China University of Petroleum(Edition of Natural Science),2010,34(1):34-36

[9] 许自龙,孟繁举,唐勇,等.叠前反演数据优化处理技术[J].石油物探,2014,53(4):404-411 Xu Z L,Meng F J,Tang Y,et al.Seismic data optimization processing techniques for prestack inversion[J].Geophysical Prospecting for Petroleum,2014,53(4):404-411

[10] Mallat S,Zhang Z.Matching pursuit with time-frequency dictionaries[J].IEEE Transactions on Signal Processing,1993,41(12):3397-3415

[11] Liu J,Wu Y,Han D,et al.Time-frequency decomposition based on Ricker wavelet[J].Expanded Abstracts of 74thAnnual Internat SEG Mtg,2004,1937-1940

[12] Liu J,Marfurt K J.Matching pursuit decomposition using Morlet wavelets[J].Expanded Abstracts of 75thAnnual Internat SEG Mtg,2005,786-789

[13] 张繁昌,李传辉,印兴耀.基于动态匹配子波库的地震数据快速匹配追踪[J].石油地球物理勘探,2010,45(5):667-673 Zhang F C,Li C H,Yin X Y.Seismic data fast matching pursuit based on dynamic matching sub-wave library[J].Oil Geophysical Prospecting,2010,45(5):667-673

[14] Wang Y H.Multichannel matching pursuit for seismic trace decomposition[J].Geophysics,2010,75(4):61-66[15] 张繁昌,李传辉.基于正交时频原子的地震信号快速匹配追踪[J].地球物理学报,2012,55(1):277-283 Zhang F C,Li C H.Seismic signal fast matching pursuit based on the orthogonal time-frequency atom[J].Chinese Journal of Geophysics,2012,55(1):277-283

[16] 张繁昌,李传辉.地震信号复数域高效匹配追踪分解[J].石油地球物理勘探,2013,48(2):171-175 Zhang F C,Li C H.Seismic signal complex domain

efficient matching pursuit decomposition[J].Oil Geophysical Prospecting,2013,48(2):171-175

[17] 杨锋涛,罗江龙,刘志强,等.相位展开的6种算法比较[J].激光技术,2008,32(3):323-326 Yang F T,Luo J L,Liu Z Q,et al.Comparison of six kinds of phase unwrapping algorithms[J].Laser Technology,2008,32(3):323-326

(编辑：陈 杰)

Seismic gathers residual moveout correction based on fast matching pursuit algorithm

Zhang Xunxun,Zhang Fanchang,Liu Hanqing

(SchoolofGeoscienceandTechnology,ChinaUniversityofPetroleum,Qingdao266580,China)

In order to extract the correct AVO information and obtain the stacking section with high SNR and high resolution,we need to eliminate residual moveout of CMP gathers by leveling reflection events.This paper presents a seismic gather residual moveout correction method based on matching pursuit algorithm.Using the advantage of the seismic signal decomposition and reconstruction of the matching pursuit algorithm,the CMP gathers signals are decomposed into different wavelets.Residual moveout correction is respectively conducted onto each wavelet,and then the corrected wavelets are used for seismic wavelet reconstruction.Moreover,in order to improve computation efficiency of the matching pursuit algorithm,we use the phase unwrapping method to get the stable instantaneous frequency and take the instantaneous frequency at envelope peak as the center to scan,and the optimal matching frequency is obtained rapidly.The theoretical model and actual data tests show that,this method not only improve the calculation efficiency,but also is good at leveling reflection events on CMP gather.

matching pursuit,phase unwrapping,signal decomposition and reconstruction,residual moveout correction

2014-10-19;改回日期：2015-01-10。

张汛汛(1991—),男,硕士在读,主要从事地球物理探测方法与技术研究。

国家重点基础研究发展计划(973计划)项目(2013CB228604)、国家自然科学基金项目(41404088)和中国石油大学(华东)研究生创新工程项目(YCX2015006)联合资助。

P631

A

1000-1441(2015)04-0420-07

10.3969/j.issn.1000-1441.2015.04.008