基于优化方法的时间-空间域隐格式有限差分算子确定方法

梁文全,王彦飞,杨长春

(1.龙岩学院资源工程学院,福建龙岩364000；2.中国科学院地质与地球物理研究所,中国科学院油气资源研究重点实验室,北京100029)

基于优化方法的时间-空间域隐格式有限差分算子确定方法

梁文全1,王彦飞2,杨长春2

(1.龙岩学院资源工程学院,福建龙岩364000；2.中国科学院地质与地球物理研究所,中国科学院油气资源研究重点实验室,北京100029)

声波方程数值模拟构成了地震逆时偏移成像技术和全波形反演的基础。对于有限差分法而言,在满足一定的稳定性条件时,普遍存在着因网格化而形成的数值频散效应。如何有效地压制数值频散是有限差分方法研究的关键所在。为了进一步抑制数值频散,利用隐式有限差分比显式有限差分更能压制数值频散的特点,采用前人提出的新的有限差分模板(在保持相同精度的情况下增大了时间步长),应用信赖域优化方法在时间-空间域确定隐格式有限差分系数。频散分析和数值模拟试算的结果表明,这种新模板隐格式有限差分优化方法既提高了声波数值模拟精度又提高了计算效率。

声波数值模拟；数值频散；隐格式有限差分；时间-空间域；信赖域优化方法

地震波场的数值模拟技术是在已知地下介质结构和参数的情况下,利用波动方程研究地震波在地下介质中的传播规律并合成地震记录的一种技术。有限差分方法因为计算效率高、所需内存小、实现简单而广泛应用于地震正演研究[1-6],同时构成了逆时偏移成像和全波形反演的基础[7-11]。

有限差分数值模拟的关键问题是数值频散和吸收边界。数值频散是对波动方程的时间和空间偏导数的离散化所造成的,使得相速度变成了网格间距的函数,这会导致地震波的数值相速度不等于地球介质的真实相速度,使得波场模拟的精度降低。一般来说,如果存在时间频散,则高频的相速度增大；如果存在空间频散,则高频的相速度减小[1]。边界条件大致有两种处理方法,一种是衰减边界条件方法(如完全匹配层等),另一种是基于单程波近似理论的吸收边界条件(ABC)方法。

偏微分方程的有限差分格式分为显式有限差分和隐式有限差分。显式有限差分格式中,某点导数的计算需要该点和它周围点的值。隐式有限差分格式中,某点导数的计算除了需要该点和它周围点的值之外,还需要它周围点的导数值[5]。众所周知,隐式有限差分格式中空间偏导数的确定需要求解三对角阵。传统的算法中,三对角阵的求逆需要较大的计算量。但是,若要达到相同的精度,使用隐式有限差分算子比使用显式有限差分算子一般需要更少的网格点。

起初,波动方程空间偏导数的有限差分算子在空间域确定。但是,地震波在时间域和空间域同时传播,因此在时间-空间域确定空间偏导数的有限差分算子能同时抑制时间频散和空间频散。Liu等[12]通过平面波理论和泰勒展开方法在时间-空间域确定有限差分算子系数。梁文全等[13]提出根据震源频率范围、波速和网格间距确定一个合适的波数范围,在此波数范围内使用线性方法确定有限差分系数,并取得良好效果。为了进一步压制频散和增加时间步长,Liu等[14]提出了使用菱形有限差分模板并确定了对应的有限差分系数。Liu等[4]也提出了新的有限差分模板,在保持相同精度的情况下增大了时间步长,并用最小二乘方法确定了相应的有限差分系数。本文应用信赖域优化方法在时间-空间域确定隐格式有限差分新模板对应的系数,以期在保证有限差分算子精度的同时提高其计算效率。

1 方法原理

二维的声波方程可以写为：

(1)

式中：p是波场；v是波速。时间二阶导数的显式有限差分算子表达式为：

(2)

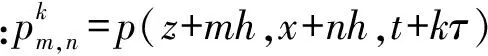
二阶空间偏导数的隐式有限差分(与以前格式略有不同,在每个方向上多了4个点)[4-5,14-16]为：

(3)

(4)

其中，

(5)

(6)

式中：cm,b和d是需要确定的交错网格有限差分系数(当d=0时为传统有限差分模板,如图1a所示；当d≠0时为新的有限差分模板,如图1b所示)。将(2)式、(3)式和(4)式代入(1)式,得到：

(7)

整理公式(7)得到：

(8)

对公式(8)进行傅里叶变换,得到：

图1 传统有限差分模板(a)和新的有限差分模板(b)

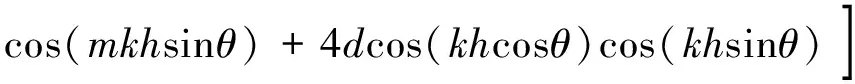
[cos(khcosθ)-1]}[2cos(ϖτ)-2]

(9)

式中：r=vτ/h。为了求得有限差分系数,建立目标函数使得速度误差最小,即：

(10)

式中：q表示需要优化的范围。其中,

(11)

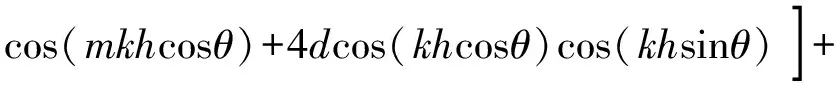
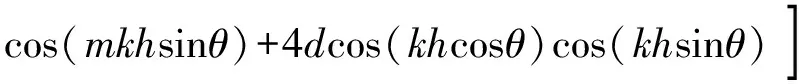
(12)

g2=2bcos(khcosθ)-2+2bcos(khsinθ)-2+

(13)

为求解φ(c)→min,我们使用信赖域方法可以得到优化的解。信赖域方法指的是[17-18]：对函数φ(c)做二次逼近,即通过第k次迭代求解(14)式所示的球约束问题,获得一个试探步长ξ,并根据公式ck+1=ck+ξk来更新优化系数。

(14)

subjectto‖ξ‖l2≤Δk

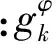
(15)

并且问题的解的表达式可以写成：

(16)

2 频散分析

有限差分方法在一个空间网格上传播的时间误差ε为[2]：

(17)

式中：δ为频散速度vFD与真实速度v的比值,即：

(18)

图2比较了传统模板的时间-空间域线性方法和新模板的时间-空间域隐格式优化方法的频散误差,其中算子长度M=7,空间间距h=20m,时间步长τ=2ms。由图2可见,时间-空间域新模板隐格式优化方法的频散误差为传统模板线性方法频散误差的1/10(注意两图的纵坐标数值相差一个数量级)。可见采用新模板隐格式优化方法可以抑制数值频散,提高地震波数值模拟的精度。

图2 传统模板线性方法(a,c,e)和新模板隐格式优化方法(b,d,f)的频散误差分析(M=7,h=20m,τ=2ms；其中,a,b的波速为1500m/s,c,d的波速为2000m/s,e,f的波速为2500m/s)

3 数值模拟试算

3.1 均匀介质模型

首先考虑均匀介质模型,对于所有的有限差分算子,v=2500m/s,τ=2ms。显式有限差分算子M=10,隐式有限差分算子M=7。计算区域划分为530×530网格,网格间距h=10m。震源在模型的中心位置,震源是高斯函数的二阶导数:

(19)

式中：f0=130Hz,f0/π是主频频率；t0=4/f0；c是常数。

图3显示了1000ms时不同有限差分算法对应的波场快照。由于使用了稀疏存储的方法和较小的算子长度,隐式有限差分方法的数值模拟耗时(141s)比显式有限差分数值模拟耗时(145s)略少,提高了计算效率。由图3可见,使用传统模板线性方法的时间频散和空间频散较大(图3a),而使用新模板隐格式优化方法同时减小了时间频散和空间频散(图3b)。

图3 均匀介质模型时间-空间域传统模板线性方法(a)和时间-空间域新模板隐格式优化方法(b)的波场快照

3.2 盐丘模型

图4显示了美国勘探地球物理学会的BP盐丘模型,其速度从1500m/s变化到4800m/s。震源位置用红色菱形表示。震源函数采用公式(12),其中震源频率f0=45Hz。对于所有的有限差分算子,空间步长h=20m。图5显示了3种不同有限差分算子在3000ms时的波形快照(z=400m),其中时间-空间域泰勒展开方法[5](蓝色曲线)的时间步长τ=1ms；时间-空间域传统模板线性方法(黑色曲线)的时间步长τ=1ms；时间-空间域新模板隐格式优化方法(红色曲线)的时间步长τ=2ms。从图5可以看到(图中红圈所示位置),新模板隐格式优化方法在时间步长τ=2ms时的频散明显小于时间-空间域泰勒展开方法在时间步长τ=1ms时的数值频散,也小于时间-空间域传统模板线性方法在时间步长τ=1ms时的数值频散。由此可见,新模板隐格式有限差分优化方法既保证了精度又提高了计算效率。

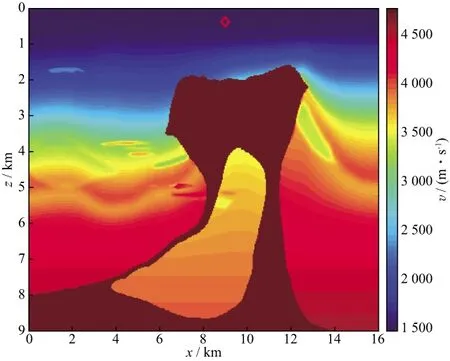
图4 BP盐丘速度模型

图5 盐丘模型3种不同有限差分算子在3000ms时的波形快照对比

4 结论

本文使用信赖域优化方法确定了新模板隐格式有限差分系数,在其它条件相同的情况下,时间步长可以从1ms增加到2ms,同时采用稀疏存储的方法,使得隐格式有限差分的计算效率得到提高。数值模拟试算结果表明,采用新模板隐格式有限差分优化方法既保证了模拟精度又提高了计算效率。

鉴于新模板隐格式有限差分优化方法能够有效抑制时间频散和空间频散,在保持相同精度的情况下增加了时间步长,因此可以代替传统的有限差分算子应用于声波数值模拟中。

[1] Dablain M A.The application of high-order differencing to the scalar wave equation[J].Geophysics,1986,51(1):54-66

[2] Liu Y.Globally optimal finite-difference schemes based on least squares[J].Geophysics,2013,78(4):T113-T132

[3] Liu Y.Optimal staggered-grid finite-difference schemes based on least-squares for wave equation modelling[J].Geophysical Journal International,2014,197(2):1033-1047

[4] Liu H,Dai N,Niu F,et al.An explicit time evolution method for acoustic wave propagation[J].Geophysics,2014,79(3):T117-T124

[5] Liu Y,Sen M K.A practical implicit finite difference method:examples from seismic modeling[J].Journal of Geophysics Engineering,2009,6(3):231-249

[6] 赵建国,史瑞其,陈竞一,等.辅助微分方程完全匹配层在声波方程数值模拟中的应用[J].吉林大学学报(地球科学版),2014,44(2):675-682 Zhao J G,Shi R Q,Chen J Y,et al.Application of auxiliary differential equation perfectly matched layer for numerical modeling of acoustic wave equations[J].Journal of Jilin University(Earth Science Edition),2014,44(2):675-682

[7] Du X,Bancroft J C,Lines L R.Anisotropic reverse-time migration for tilted TI media[J].Geophysical Prospecting,2007,55(6):853-869

[8] Liu H W,Li B,Liu H,et al.The issues of prestack reverse time migration and solutions with Graphic Processing Unit implementation[J].Geophysical Prospecting,2012,60:906-918

[9] Xie W,Yang D,Liu F,et al.Reverse-time migration in acoustic VTI media using a high-order stereo operator[J].Geophysics,2014,79(3):WA3-WA11

[10] Yan H,Liu Y.Acoustic VTI modeling and pre-stack reverse-time migration based on the time-space domain staggered-grid finite-difference method[J].Journal of Applied Geophysics,2013,90(1):41-52

[11] Yan H,Liu Y.Visco-acoustic prestack reverse-time migration based on the time-space domain adaptive high-order finite-difference method[J].Geophysical Prospecting,2013,61(5):941-954

[12] Liu Y,Sen M K.Scalar wave equation modeling with time-space domain dispersion-relation-based staggered-grid finite-difference schemes[J].Bulletin of the Seismological Society of America,2011,101(1):141-159

[13] 梁文全,杨长春,王彦飞,等.用于声波方程数值模拟的时间-空间域有限差分系数确定新方法[J].地球物理学报,2013,56(10):3497-3506 Liang W Q,Yang C C,Wang Y F,et al.Acoustic wave equation modeling with new time-space domain finite difference operators[J].Chinese Journal of Geophysics,2013,56(6):840-850

[14] Liu Y,Sen M K.Time-space domain dispersion-relation-based finite-difference method with arbitrary even-order accuracy for the 2D acoustic wave equation[J].Journal of Computational Physics,2013,232(1):327-345

[15] Tan S,Huang L.An efficient finite-difference method with high-order accuracy in both time and space domains for modelling scalar-wave propagation[J].Geophysical Journal International,2014,197(2):1250-1267

[16] Tan S,Huang L.A staggered-grid finite-difference scheme optimized in the time-space domain for modeling scalar-wave propagation in geophysical problems[J].Journal of Computational Physics,2014,276:613-634

[17] Wang Y F,Yuan Y X.Convergence and regularity of trust region methods for nonlinear ill-posed inverse problems[J].Inverse Problems,2005,21(3):821-838

[18] 王彦飞.反演问题的计算方法及其应用[M].北京：高等教育出版社,2007:1-370 Wang Y F.Computational methods for Inverse problems and applications[M].Beijing:Higher Education Press,2007:1-370

(编辑：顾石庆)

Determination on the implicit finite-difference operator based on optimization method in time-space domain

Liang Wenquan1,Wang Yanfei2,Yang Changchun2

(1.CollegeofResourceEngineering,LongyanUniversity,Longyan364000,China；2.KeyLaboratoryofPetroleumResourcesResearch,InstituteofGeologyandGeophysics,ChineseAcademyofSciences,Beijing100029,China)

Numerical simulation of acoustic wave equation is the basis of the reverse time migration and full waveform inversion. With some stability conditions,grid dispersion often exists because of the discretization of the time and the spatial derivatives in the wave equation. How to suppress the grid dispersion is therefore a key problem for finite difference approaches. Finite-difference scheme of partial differential equations are either explicit or implicit. Implicit finite difference scheme can suppress the grid dispersion further. Meanwhile,a new finite difference stencil was proposed to increase the time step while preserving the accuracy by previous researchers. Therefore,we propose to determine the optimal implicit finite difference operators in time-space domain with a new finite difference stencil. Dispersion analysis and seismic numerical simulation demonstrate that the accuracy of acoustic wave numerical simulation and the computation efficiency can be improved by the method.

acoustic wave numerical simulation,grid dispersion,implicit finite difference scheme,time-space domain,trust region optimization method

2014-10-17;改回日期：2014-12-29。

梁文全(1983—)，男，讲师，现主要研究方向为地震波数值模拟及偏移成像。

国家自然科学基金(41325016,11271349)、国家重大科研装备研制项目(ZDYZ2012-1-02-04)、龙岩学院博士科研启动基金(LB2014010)和福建省教育厅JK项目(2014050)联合资助。

P631

A

1000-1441(2015)03-0254-06

10.3969/j.issn.1000-1441.2015.03.002